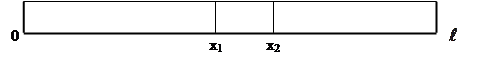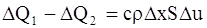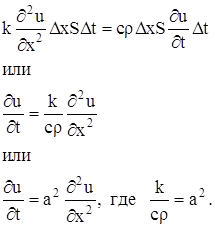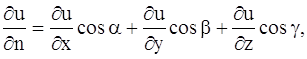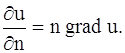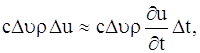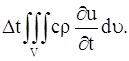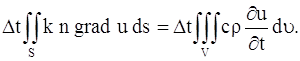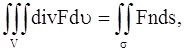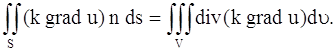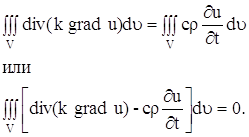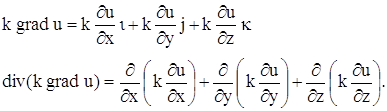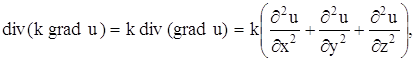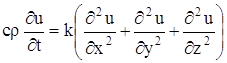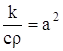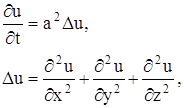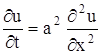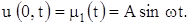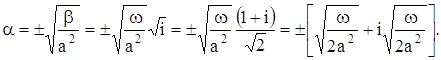Уравнение распределения температуры в стержне

Электронная библиотека

Если тепловые источники отсутствуют, то температура однородного стержня удовлетворяет уравнению теплопроводности (4.44).

Будем полагать, что задан режим (начальное условие) (4.35). Предположим также, что концы стержня и имеют температуру, равную нулю (говорят, что это температура внешней среды), т.е. имеем простейшие краевые условия (4.35) при любом .

Для уравнения (4.44) сначала будем искать ненулевые решения вида:

где, как и ранее, – функция одной переменной , а – переменного . Так как

то, подставив эти значения производных в уравнение (4.44.), получим:

Отсюда, разделив переменные, будем иметь:

(знак «минус» взят, потому что другие значения не дадут нужных решений). Получаем из (4.47) два обыкновенных дифференциальных уравнения:

Первое уравнение имеет общее решение:

где и – произвольные постоянные.

Второе уравнение дает общее решение:

где – произвольная постоянная. Перемножая функции , получим:

где . Функции (4.50), при любом виде удовлетворяют уравнению (4.44). Потребуем, чтобы они удовлетворяли также краевым условиям (4.35). Положим , получим , отсюда . Следовательно,

Но , ибо имели бы нулевое решение.

Положим , в силу условия (4.35) будем иметь:

Но , ибо тогда . Поэтому , откуда находим или . Эти числа называются характеристическими числами задачи, а совокупность их спектром задачи. Каждому соответствует частное решение уравнения теплопроводности:

Замечание. В качестве п достаточно брать лишь целые положительные числа (n = 1,2,…), так как при п = 0 имеем , что противопоказано, а при п 0.

Решение. Задача сводится к решению уравнения:

удовлетворяющего начальному условию U(x, 0) = U₀ и граничным условиям , и (условие теплоизоляции конца х = 0 означает, что ).

Применяя метод Фурье, найдем, что уравнение (4.44) имеет решение:

Из граничных условий получим:

Из первого уравнения следует, что ибо (получили бы нулевое решение), из второго уравнения следует, что . Решая второе уравнение, получим: . В результате имеем бесчисленное множество решений:

удовлетворяющих граничным условиям.

Решение задачи ищем в виде ряда:

Из начального условия получим:

Эта формула позволит найти . Для этого разложим в ряд Фурье четную функцию, имеющую период 4l и равную при –l Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Уравнение распространения тепла в стержне

2.1.1. Уравнение распространения тепла в стержне.

Рассмотрим однородный стержень длины 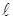. Будем предполагать, что боковая поверхность стержня теплонепроницаема и что во всех точках поперечного сечения стержня температура одинакова. Изучим процесс распространения тепла в стержне.

Расположим ось Ох так, что один конец стержня будет совпадать с точкой х = 0, а другой – с точкой х = .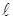

Пусть u (x, t) – температура в сечении стержня с абсциссой х в момент t. Опытным путем установлено, что скорость распространения тепла, т. е. количество тепла, протекающего через сечение с абсциссой х за единицу времени, определяется формулой

(1)

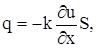
где S – площадь сечения рассматриваемого стержня, k – коэффициент теплопроводности.

Рассмотрим элемент стержня, заключенный между сечениями с абсциссами х₁ и х₂ (х₂ – х₁ = х). Количество тепла, прошедшего через сечение с абсциссой х₁ за время t, будет равно

(2)

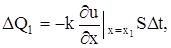
то же самое с абсциссой х₂:

(3)

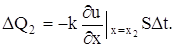
Приток Q₁ — Q₂ в элемент стержня за время t будет равняться:

(4)

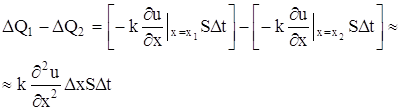
Этот приток тепла за время t затратился на повышение температуры элемента стержня на величину u:

(5)

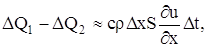
где с – теплоемкость вещества стержня, 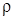– плотность вещества стержня (xS – масса элемента стержня).

Приравнивая выражения (4) и (5) одного и того же количества тепла 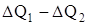, получим:

Это и есть уравнение распространения тепла (уравнение теплопроводности) в однородном стержне.

Чтобы решение уравнения (6) было вполне определено, функция u (x, t) должна удовлетворять краевым условиям, соответствующим физическим условиям задачи. Краевые условия для решения уравнения (6) могут быть различные. Условия, которые соответствуют так называемой первой краевой задаче для 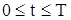, следующие:

u (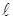, t) = ψ₂(t). (9)

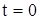
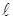
Физическое условие (7) (начальное условие) соответствует тому, что при в разных сечениях стержня задана температура, равная φ(x). Условия (8) и (9) (граничные условия) соответствуют тому, что на концах стержня при х = 0 и при х = поддерживается температура, равная ψ₁(t) и ψ₂(t) соответственно.

Доказывается, что уравнение (6) имеет единственное решение в области 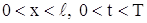, удовлетворяющее условиям (7) – (9).

2.1.2. Распространение тепла в пространстве.

Рассмотрим процесс распространения тепла в трехмерном пространстве. Пусть u (x, y, z, t) – температура в точке с координатами (x, y, z) с момент времени t. Опытным путем установлено, что скорость прохождения тепла через площадку s, т. е. количество тепла, протекающего за единицу времени, определяется формулой (аналогично формуле (1))

(10)

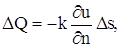
где k – коэффициент теплопроводности рассматриваемой среды, которую мы считаем однородной и изотропной, n – единичный вектор, направленный по нормали к площадке s в направлении движения тепла. Таким образом, можем записать:

где – направляющие косинусы вектора n, или

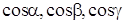
Подставляя выражение 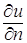в формулу (10), получаем:

Q = -k n grad u s.

Количество тепла, протекающего за время ∆t через площадку ∆s, будет равно:

Qt = -k n grad u t s.

Вернемся к поставленной задаче. В рассматриваемой среде выделим малый объем V, ограниченный поверхностью S. Количество тепла, протекающего через поверхность S, будет равно:

(11)

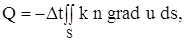
где n – единичный вектор, направленный по внешней нормали к поверхности S. Очевидно, что формула (11) дает количество тепла, поступающего в объем V (или уходящего из объема V) за время t. Количество тепла, поступившего в объем V, идет на повышение температуры вещества этого объема.

Рассмотрим элементарный объем υ. Пусть за время t его температура поднялась на u. Очевидно, что количество тепла, затраченное на это повышение температуры элемента υ, будет равно

где с – теплоемкость вещества, ρ – плотность. Общее количество тепла, затраченное на повышение температуры в объеме V за время t, будет

Но это есть тепло, поступающее в объем V за время t; оно определено формулой (11) . Таким образом, имеет место равенство

Сокращая на t, получаем:

(12)

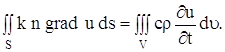
Поверхностный интеграл, стоящий в левой части этого равенства, преобразуем по формуле Остроградского (в векторной форме, где F – дивергенция векторного поля, 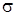– замкнутая поверхность)

полагая F = k grad u:

Заменяя двойной интеграл, стоящий в левой части равенства (12), тройным интегралом, получим:

Применив теорему о среднем к тройному интегралу, стоящего слева, получим :

(14)

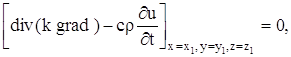
где P (x, y, z) – некоторая точка объема V.

Так как мы можем выделить произвольный объем V в трехмерном пространстве, где происходит распространение тепла, и так как мы предполагаем, что подынтегральная функция в равенстве (13) непрерывна, то равенство (14) будет выполняться в каждой точке пространства. Итак,

(15)

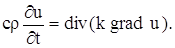
Подставляя в уравнение (15), получаем:

(16)

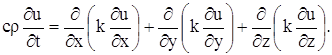
Если k – постоянное, то

и уравнение (15) в этом случае дает:

или, положив

(17)

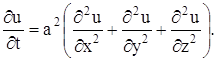
Коротко уравнение (17) записывается так:

где u – оператор Лапласа. Уравнение (17) и есть уравнение теплопроводности в пространстве. Для того чтобы найти единственное решение, отвечающее поставленной задаче, нужно задать краевые условия.

Пусть имеем тело , поверхность которого . В этом теле рассматривается процесс распространения тепла. В начальный момент температура тела задана. Это соответствует тому, что известно значение решения при t = 0 – начальное условие:

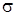
u (x, y, z, 0) = φ (x, y, z). (18)

Кроме того, должна быть известна температура в любой точке М поверхности 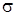тела в любой момент времени t – граничное условие:

u (М, t) = ψ (М, t). (19)

(Возможны и другие граничные условия.)

Если искомая функция u (x, y, z, t) не зависит от z, что соответствует тому, что температура не зависит от z, то получаем уравнение:

(20)

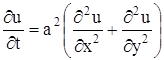
— уравнение распространения тепла на плоскости. Если рассматривается распространения тепла в плоской области D с границей С, то граничные условия, аналогично (18) и (19), формулируются так:

где φ и ψ – заданные функции, М – точка границы С.

Если же функция u не зависит ни от z, ни от y, то получаем уравнение

— уравнение распространения тепла в стержне.

§2.2. Температурные волны.

Задача о распространении температурных волн в почве является одним из первых примеров приложения математической теории теплопроводности, развитой Фурье, к изучению явлений природы.

Температура на поверхности земли носит, как известно, ярко выраженную суточную и годовую периодичность. Обратимся к задаче о распространении периодических температурных колебаний в почве, которую будем рассматривать как однородное полупространство 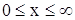. Эта задача является характерной задачей без начальных условий, так как при многократном повторении температурного хода на поверхности влияние начальной температуры будет меньше влияния других факторов, которыми мы пренебрегаем (например, неоднородность почвы). Таким образом, приходим к следующей задаче:

найти ограниченное решение уравнения теплопроводности

(1)

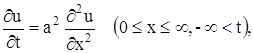
u (0, t) = A cos 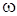t. (2)

Предполагается, что функции u (x, t) и m (t) ограничены всюду, т.е.

Запишем граничное условие в виде

(2’)

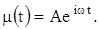
Из линейности уравнения теплопроводности следует, что действительная и мнимая части некоторого комплексного решения уравнения теплопроводности каждая в отдельности удовлетворяет тому же решению.

Если найдено решение уравнения теплопроводности, удовлетворяющее условию (2’), то его действительная часть удовлетворяет условию (2), а мнимая – условию

Итак, рассмотрим задачу:

(3)

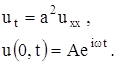
Ее решение будем искать в виде

(4)

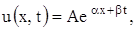
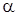
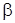
где и — неопределенные пока постоянные.

Подставляя выражение (4) в уравнение (3) и граничное условие, находим:

,

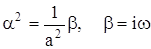
Для u (x, t) имеем:

(5)

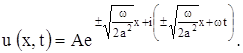
Действительная часть этого решения

(6)

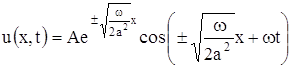
удовлетворяет уравнению теплопроводности и граничному условию (2). Формула (6) в зависимости от выбора знака определяет не одну, а две функции. Однако только функция, соответствующая знаку минус, удовлетворяет требованию ограниченности. Таким образом, решение поставленной задачи получаем в виде

(7)

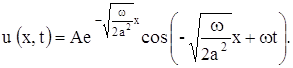
На основании полученного решения можно дать следующую характеристику процесса распространения температурной волны в почве. Если температура поверхности длительное время периодически меняется, то в почве также устанавливаются колебания температуры с тем же периодом, причем:

1.Амплитуда колебаний экспоненционально убывает с глубиной

,

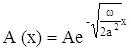
т.е. если глубины растут в арифметической прогрессии, то амплитуды убывают в геометрической прогрессии (первый закон Фурье).

2. Температурные колебания в почве происходят со сдвигом фазы. Время 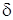запаздывания максимумов (минимумов) температуры в почве от соответствующих моментов на поверхности пропорционально глубине

Распределение температуры в стержне с двусторонним подводом тепла Текст научной статьи по специальности « Физика»

Аннотация научной статьи по физике, автор научной работы — Видин Юрий Владимирович, Иванов Дмитрий Иванович, Казаков Роман Владимирович

С использованием аналитических зависимостей произведен расчет распределения температуры в стержне с двусторонним подводом тепла, определены координаты экстремумов. Показано, что для такого стержня с уменьшением избыточной температуры на конце стержня при фиксированном значении избыточной температуры у его основания величина минимального температурного напора существенно снижается.

Похожие темы научных работ по физике , автор научной работы — Видин Юрий Владимирович, Иванов Дмитрий Иванович, Казаков Роман Владимирович

The authors have calculated temperature distribution in a rod with double-end heat supply and determined extreme values coordinates using the analytical dependences. It was shown that the value of minimum temperature drop decreases considerably for such rod at excess temperature depression at the end of the rod at non-variable value of the excess temperature at its base.

Текст научной работы на тему «Распределение температуры в стержне с двусторонним подводом тепла»

РАСПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ В СТЕРЖНЕ С ДВУСТОРОННИМ ПОДВОДОМ ТЕПЛА

Ю.В. Видин, Д.И. Иванов, Р.В. Казаков

Сибирский федеральный университет, г. Красноярск E-mail: idi86@inbox.ru

С использованием аналитических зависимостей произведен расчет распределения температуры в стержне сдвусторонним подводом тепла, определены координаты экстремумов. Показано, что для такого стержня суменьшением избыточной температуры на конце стержня при фиксированном значении избыточной температуры у его основания величина минимального температурного напора существенно снижается.

Стационарный теплообмен, аналитические методы расчета температурных полей, развитые поверхности теплообмена.

Stationary heat transfer, analytical methods for calculating the temperature fields, developed heat exchange surface.

В теплотехнике для существенной интенсификации процессов теплообмена широко используются оребрённые поверхности [1, 2]. Как правило, подвод тепла в таких конструкциях происходит через основание ребра, т. е. является односторонним. Однако на практике могут иметь место случаи, когда стержни конечной длины связывают между собой две теплоотдающие поверхности, обладающие разными температурами. Тогда при условии, что соединительный элемент постоянного поперечного сечения, задача переноса тепла вдоль такого тела может быть записана в виде

где 3=—с — избыточная температура, °С; 30=10-1с, 3=Ь^с — избыточные температуры на концах рассматриваемого стержня, °С; ¡С — температура окружающей среды стержня, °С; I — длина стержня, мм;

где а, X — коэффициенты теплоотдачи и теплопроводности соответственно; Р=2(а+Ь), /=аЬ — периметр и площадь поперечного сечения тела, где а, Ь — толщина и ширина ребра соответственно.

При условии, что Ь>а, параметр т можно представить в виде

Решение дифференциального уравнения (1) известно [1]

3 = С1етх + С2е-тх. (4)

Постоянные интегрирования С1 и С2 находим из граничных условий (2) и (3):

eml — e ml 3, -30eml

Подставляя (5) и (6) в зависимость (4), получим

3=3 sh[m(l-х)] +3 sh(mx)

— гиперболический синус, кото-

рый относится к классу элементарных функций [3, 4].

Особенный инженерный интерес представляет месторасположение экстремума температуры по длине стержня и её величина.

Для этого, дифференцируя выражение (7), находим производную

_ сЬ[т(/ — х)] й сЬ(тх)

Из ур. (8), при условии, что — = 0, получим

Ч0сЬ[т(/ — х*)] = Ч^Цтх* ], (9)

где х* — осевая координата экстремума функции (7). Принимая во внимание, что гиперболический кос-

инус равен сЬ2 =———— можно на основе соотно-

шения (9) выразить координату х* в следующем виде:

Очевидно, что при й=й Х*=1/2, т. е. тепловой центр окажется в середине стержня.

Из выражения (10) также следует, что если отношения избыточных температур на концах стержні

будет иметь значение

В качестве примера рассмотрим стержень прямоугольного сечения /=100 мм, изготовленный из стали, А=50 Вт/(м-К), размеры которого ахй=5х100 мм.

Коэффициент теплоотдачи на поверхности стержня примем а=20 Вт/(м2-К).

Следовательно, параметр т равен 17,89 м-1.

Для л=0 примем температуру основания (,=100 °С. На противоположной стороне х=100 мм рассмотрим три варианта: ^=90, 80, 70 °С.

Во всех случаях температура среды одна и та же и равна (¿=20 °С.

На рис. 1 приведены кривые изменения избыточной температуры для указанных трех случаев.

Рис. 1. Кривые изменения температуры стержня для значений температуры =90, 80, 70 °С

При дальнейшем снижении температуры на противоположном основанию конце стержня экстремум функции покидает пределы стержня.

На рис. 2 приведены кривые изменения избыточной температуры стержня для значений ^=60, 50 °С.

то экстремум температуры сместится в сторону менее нагретого основания, и координата х* станет равной его длине, т. е. х*=1. Если по условию задачи

величина — окажется меньше, чем рассчитанная чо

по (11), то, следовательно, экстремум температуры уйдет за пределы длины рассматриваемого ребра.

Подставляя (10) в формулу (7), несложно рассчитать минимальную избыточную температуру по длине стержня.

Вычислив на основе зависимости (10) координату х*, далее также можно рассчитать коэффициенты тепловой эффективности первой и второй частей стержня по формулам [4]:

О ш II I =50 °С 38 °С

20 40 60 80 100′

Рис. 2. Кривые изменения температуры стержня для значений температуры =60, 50 °С

Разработаны аналитические зависимости для расчета избыточных температур по длине стержня при двустороннем подводе тепла в зависимости от температур на концах рассматриваемого стержня и теплофизических свойств на основании элементарных функций. Произведены расчеты избыточных температур по длине стального стержня, результаты которых показали, что с уменьшением избыточной температуры на конце стержня при фиксированном значении температуры у его основания экстремум избыточной температуры стержня смещается вправо, и величина минимального температурного напора существенно снижается.

1. Керн Д., Краус А. Развитые поверхности теплообмена. — М.: Энергия, 1977. — 461 с.

2. Гольберг А.И., Корягин В.С., Мочан С.И., Тынтарев Э.М. Расчет и проектирование цельносварных экранов котельных агрегатов. — Л.: Энергия, 1975. — 272 с.

3. Сегал Б.И., Семендяев К.А. Пятизначные математические таблицы. — М.: Изд-во АН СССР. 1950. — 464 с.

4. Видин Ю.В., Бойков ГП., Колосов В.В., Ромащенко А.С. Краткий справочник по тепломассообмену. — Красноярск: Сибирский федеральный университет, 2007. — 169 с.

Поступила 01.03.2012 г.

ЭФФЕКТИВНОСТЬ ЗАМЕНЫ ПАРОВОГО ТУРБОПРИВОДА МЕХАНИЗМОВ СОБСТВЕННЫХ НУЖД ЭНЕРГОБЛОКОВ ТЭС ГАЗОТУРБИННЫМ ПРИВОДОМ

Томский политехнический университет E-mail: gal@tpu.ru

Получено уравнение, позволяющее на основе срока окупаемости определить экономическую целесообразность замены парового турбопривода механизма собственных нужд энергоблоков ТЭС газотурбинным двигателем в зависимости от стоимости электроэнергии и топлива и стоимостных и режимных показателей газотурбинных двигателей.

Механизм собственных нужд; энергоблок, паровой турбопривод; газотурбинный двигатель; срок окупаемости.

Auxiliary mechanism; power block; steam turbine drive; gas turbine engine; payback period.

Одним из главных направлений развития электроэнергетики на современном этапе является повышение эффективности выработки электроэнергии на основе современных энерго- и ресурсосберегающих технологий [1]. В настоящее время в энергетике к таким технологиям можно отнести установки с газотурбинными двигателями (ГТД). В последнее время газотурбинные двигатели очень быстро совершенствуются: их КПД растет, и даже для простого цикла достиг 40. 45 %, а стоимость существенно снижается: в 3.4 раза ниже, чем для паротурбинных установок. На ТЭС пока ГТД используется для привода электрогенераторов: самостоятельно или в комбинации с паротурбинными установками в парогазовых установках. Но на ТЭС имеется большое количество механизмов собственных нужд, которые в качестве привода используют электродвигатели или паровые турбины.

Увеличение отпуска электроэнергии за счет сокращение затрат энергии на собственные нужды является актуальной задачей при эксплуатации, проектировании и модернизации ТЭС и существенным источником энергосбережения. Так, применение паротурбинного привода питательных насосов на энергоблоках сверхкритического давления позволило сократить расход электроэнергии на собственные нужды на 2.2,5%. Анаразраба-тываемых энергоблоках нового поколения на су-перкритические параметры пара применение паротурбинного привода питательных насосов позво-

лит сократить расход электроэнергии на собственные нужды на 3.3,5 %.

Как показано в [2] паровой турбопривод при большой мощности экономичнее электродвигателей, поэтому в настоящее время на всех энергоблоках сверхкритических параметров для питательных насосов и для воздуходувок на блоках 500, 800 МВт он установлен в качестве привода.

Паровой турбопривод позволяет: идеально регулировать производительность механизмов изменением частоты вращения; выполнить механизмы на высокое число оборотов, что улучшает их показатели, уменьшает габариты и стоимость; увеличить полезный отпуск электроэнергии при одинаковой мощности турбогенератора из-за уменьшения ее на электропривод; уменьшить затраты на систему питания электропривода и снизить токи короткого замыкания; увеличить устойчивость режима работы механизмов, благодаря отсутствию влияния колебания частоты тока на их производительность. К недостаткам парового турбопривода следует отнести то, что усложняется тепловая схема энергоблока и электростанции; требуется подача пара на турбопривод от пусковой котельной или через резервные паропроводы от других энергоблоков при пуске энергоблока.

Достоинства, которые имеет паровой турбопривод, обеспечивает также ГТД. В последнее время ГТД даже при небольшой мощности уже достигли эффективного КПД 30.35 % [3]. Замена газотур-