Уравнение расстояния между прямой и плоскостью

Расстояние между прямой и параллельной ей плоскостью – определение и примеры нахождения.

В этой статье дано определение расстояния между параллельными прямой и плоскостью, приведена теория, необходимая для нахождения расстояния между прямой и параллельной ей плоскостью методом координат, а также подробно разобраны решения характерных примеров и задач.

Навигация по странице.

Расстояние между параллельными прямой и плоскостью – определение.

Расстояние между прямой и параллельной ей плоскостью определяется через расстояние от точки до плоскости.

Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

Рассмотрим прямую a и параллельную ей плоскость . Отметим на прямой a точку M₁ и опустим перпендикуляр M₁H₁ из этой точки на плоскость . Длина перпендикуляра M₁H₁ есть расстояние между заданными параллельными прямой и плоскостью.

Озвученное определение расстояния между параллельными прямой и плоскостью тесно связано со следующей теоремой.

Если прямая a параллельна плоскости , то все точки прямой a равноудалены от плоскости .

Проведем через произвольную точку прямой a плоскость параллельно плоскости . Прямая a при таком построении плоскости лежит в этой плоскости (если бы это было не так, то прямая a пересекала бы плоскость , а, значит, пересекала бы и плоскость в силу параллельности плоскостей и ). В статье расстояние между параллельными плоскостями мы доказали теорему о том, что все точки одной из параллельных плоскостей находятся на одинаковом расстоянии от другой плоскости. Следовательно, все точки прямой a , которая лежит в плоскости , параллельной плоскости , равноудалены от плоскости , что и требовалось доказать.

Нахождение расстояния между прямой и параллельной ей плоскостью – теория, примеры, решения.

Расстояние между параллельными прямой и плоскостью обычно находится с помощью методов, изученных на уроках геометрии в 10-11 классах, — с использованием теоремы Пифагора, признаков равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п.

Когда в трехмерном пространстве введена прямоугольная система координат и требуется вычислить расстояние между заданными параллельными прямой и плоскостью, то применяется метод координат. Сейчас мы его подробно разберем, после чего рассмотрим решения нескольких примеров.

Поставим перед собой следующую задачу.

Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы параллельные прямая a и плоскость , и требуется найти расстояние между прямой a и плоскостью .

Решение этой задачи будем строить на основе определения расстояния между прямой и параллельной ей плоскостью.

Искомое расстояние между заданными параллельными прямой и плоскостью по определению равно расстоянию от точки М₁ , лежащей на прямой a , до плоскости . Если мы определим координаты некоторой точки М₁ , лежащей на прямой a , и получим нормальное уравнение плоскости в виде , то мы сможем вычислить искомое расстояние , применив формулу (эта формула была получена в разделе нахождение расстояния от точки до плоскости).

Итак, алгоритм, позволяющий найти расстояние между параллельными прямой a и плоскостью , таков:

• находим координаты некоторой точки М₁ , лежащей на заданной прямой a (это легко сделать, если знать основные виды уравнений прямой в пространстве);
• получаем нормальное уравнение заданной плоскости вида (для этого нужно знать основные виды уравнения плоскости и при необходимости уметь приводить уравнение плоскости к нормальному виду);
• вычисляем требуемое расстояние между прямой a и параллельной ей плоскостью по формуле .

Воспользуемся полученным алгоритмом при решении задач, в которых требуется вычислить расстояние между параллельными прямой и плоскостью.

Найдите расстояние между параллельными прямой и плоскостью .

Очевидно, точка лежит на прямой, которую определяют канонические уравнения прямой в пространстве .

Получим нормальное уравнение плоскости . Для этого приведем заданное общее уравнение плоскости к нормальному виду: вычисляем нормирующий множитель , умножаем на него обе части заданного общего уравнения плоскости .

Осталось вычислить требуемое расстояние между заданными параллельными прямой и плоскостью как расстояние от точки до плоскости :

Найдите расстояние между прямой и параллельной ей плоскостью .

В рассматриваемой задаче прямая задана уравнениями двух пересекающихся плоскостей. Найдем координаты некоторой точки М₁ , лежащей на этой прямой. Координаты точки М₁ должны удовлетворять уравнениям прямой, то есть, — частное решение системы линейных уравнений . Найдем частное решение этой системы (при необходимости смотрите статью решение систем линейных уравнений). Приняв , приходим к системе уравнений , откуда находим . То есть, имеем .

Теперь получим нормальное уравнение плоскости, которую задает уравнение плоскости в отрезках вида . Для этого переходим к общему уравнению плоскости . Полученное общее уравнение плоскости уже является нормальным уравнением плоскости и его не нужно приводить к нормальному виду.

Осталось вычислить расстояние от точки до плоскости , которое равно искомому расстоянию между параллельными прямой и плоскостью: .

Расстояние между прямой и параллельной ей плоскостью: определение и примеры нахождения

В статье ниже мы найдем определение, что же представляет собой расстояние между прямой и плоскостью, параллельными друг другу; разберем способ определить это расстояние и применим полученный навык в решении конкретных задач.

Расстояние между прямой и параллельной ей плоскостью: определение

Расстояние между прямой и параллельной ей плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.

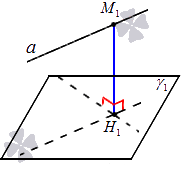
Пусть нам даны прямая a и плоскость ϒ 1 , ей параллельная. Используем некоторую точку М 1 , принадлежащую прямой a : проведем перпендикуляр из этой точки на заданную плоскость. Основание перпендикуляра на плоскости обозначим как Н 1 . Длина перпендикуляра М 1 Н 1 и будет являться расстоянием между исходными параллельными прямой и плоскостью.

Указанное определение имеет тесную взаимосвязь со следующей теоремой.

Когда прямая a параллельна плоскости ϒ 1 , все точки прямой a находятся на одинаковом расстоянии от плоскости ϒ 1 .

Используем любую произвольную точку на прямой a – проведем через нее плоскость ϒ 2 , параллельную заданной плоскости ϒ 1 . В таком построении прямая а принадлежит плоскости ϒ 2 (в ином случае прямая а пересекала бы эту плоскость, а, следовательно, пересекала бы и плоскость ϒ 1 , что противоречит исходному условию). В статье, которая разбирает тему расстояния между параллельными плоскостями, мы доказали теорему о том, что все точки одной из параллельных плоскостей равноудалены от точек другой плоскости. Таким образом, все точки прямой a , принадлежащей плоскости ϒ 2 (в свою очередь, параллельной плоскости ϒ 1 ) находятся на одинаковом расстоянии от плоскости ϒ 1 . Что и требовалось доказать.

Нахождение расстояния между параллельными прямой и плоскостью

Искомое расстояние между параллельными прямой и плоскостью обычно находится с использованием теоремы Пифагора, признаков равенства или подобия треугольников и пр.

Если же в трехмерном пространстве задана прямоугольная система координат, мы можем применить метод координат. Разберем его подробнее.

Допустим, в трехмерном пространстве зафиксирована некоторая прямоугольная система координат O x y z , в которой заданы прямая a и плоскость ϒ 1 , параллельные между собой. Требуется определить расстояние между заданными прямой и плоскостью.

Построим решение этой задачи на указанном выше определении расстояния между прямой и параллельной ей плоскостью.

Используем некоторую точку М 1 , принадлежащую прямой a : расстояние от этой точки до заданной плоскости и будет являться искомым расстоянием между параллельными прямой и плоскостью. Определим координаты точки М 1 как ( x 1 , y 1 , z 1 ) и запишем нормальное уравнение плоскости ϒ 1 : cos α · x + cos β · y + cos γ · z — p = 0 . Теперь мы можем вычислить искомое расстояние, для чего применим формулу:

M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p

Вывод этой формулы можно изучить в статье о нахождении расстояния от точки до плоскости.

Таким образом, мы можем сформулировать алгоритм для нахождения расстояния между прямой и параллельной ей плоскостью:

— определяем координаты точки, принадлежащей заданной прямой (для этого пригодятся навыки работы с основными видами уравнений в пространстве);

— записываем нормальное уравнение заданной плоскости вида cos α · x + cos β · y + cos γ · z — p = 0 (чтобы легко справиться с этим пунктом, следует повторить материал по основным видам уравнений плоскости и вспомнить навык приведения уравнения плоскости к нормальному виду);

— вычисляем искомое расстояние по формуле: M 1 H 1 = cos α · x 1 + cos β · y 1 + cos γ · z 1 — p

Задана прямая x — 1 2 = y 0 = z + 1 1 и параллельная ей плоскость 3 x + 2 y — 6 z — 2 = 0 . Необходимо определить расстояние между ними.

Решение

Заданные условием задачи канонические уравнения прямой x — 1 2 = y 0 = z + 1 1 дают возможность определить точку М 1 ( 1 , 0 , — 1 ) , принадлежащую этой прямой.

Запишем нормальное уравнение исходной плоскости, т.е. преобразуем заданное условием задачи общее уравнение в нормальный вид. Вычислим нормирующий множитель: 1 3 2 + 2 2 + ( — 6 ) 2 = 1 7 и умножим на него обе части исходного общего уравнения плоскости:

3 x + 2 y — 6 z — 2 = 0 ⇔ 1 7 · 3 x + 2 y — 6 z — 2 = 1 7 · 0 ⇔ 3 7 x + 2 7 y — 6 7 z — 2 7

Теперь можем вычислить требуемое расстояние как расстояние от точки М 1 до плоскости 3 7 x + 2 7 y — 6 7 z — 2 7 = 0 :

M 1 H 1 = 3 7 · 1 + 2 7 · 0 — 6 7 · — 1 — 2 7 = 1

Ответ: 1 .

Заданы прямая 2 x — y + 9 = 0 2 x + y — 2 z + 3 = 0 и параллельная ей плоскость x — 3 2 + y 3 2 + z — 3 = 1 . Необходимо найти расстояние между ними.

Решение

Условием задачи прямая описывается уравнениями двух пересекающихся плоскостей. Определим координаты ( x 1 , y 1 , z 1 ) некой точки М 1 , принадлежащей этой прямой. Искомые координаты должны отвечать условиям уравнений прямой, т.е. координаты ( x 1 , y 1 , z 1 ) будут частным решением системы линейных уравнений 2 x — y + 9 = 0 2 x + y — 2 z + 3 = 0 . Найдем частное решение этой системы.

Примем z = 0 , тогда получим: 2 x — y = — 9 2 x + y = — 3 , откуда x = — 3 , y = 3 .

Таким образом, координаты точки М 1 равны ( — 3 , 3 , 0 ) .

Теперь запишем нормальное уравнение плоскости, заданной условием задачи уравнением плоскости в отрезках. Сначала осуществим переход к общему уравнению плоскости:

x — 3 2 + y 3 2 + z — 2 = 1 ⇔ — 2 3 x + 2 3 y — 1 3 z — 1 = 0

Полученное общее уравнение уже является нормальным уравнением плоскости, поэтому в дальнейших преобразованиях необходимости нет.

Наконец, вычислим расстояние от точки до плоскости, которое и будет являться требуемым расстоянием от заданной прямой к заданной плоскости:

M 1 H 1 = — 2 3 · — 3 + 2 3 · 3 — 1 3 · 0 — 1 = 0 = 3

Метод координат

Для решения задачи по стереометрии координатным методом нужно выбрать декартову систему координат. Ее можно выбрать как угодно, главное, чтобы она была удобной. Приведем примеры выбора системы координат в кубе, пирамиде и конусе:

Далее необходимо найти координаты основных точек в выбранной системе координат. Это могут быть вершины объемной фигуры, середины ребер или любые другие точки, указанные в условии задачи. Найдем координаты куба и правильной пирамиды (предположим, что все ребра равны \(4\)):

Куб: Очевидно, что координаты точки \(A\) в начале координат — \((0;0;0)\). т. \(B\) — \((4;0;0)\), т. \(G\) — \((4;4;4)\) и т.д. (Рис. 1).

С кубом все просто, но в других фигурах могут возникнуть трудности с нахождением координат.

Давайте рассмотрим правильную пирамиду \(ABCD\):

У \(т. A\) координаты \((0;0;0)\), потому что она лежит в начале координат.

Координату \(x\) точки \(С\) можно получить, опустив перпендикуляр \(CE\) из \(т.С\) на ось \(OX\). (см. Рис. 2). Получится \(т.E\), указывающая на искомую координату по \(x\) – 2.

Координату \(y\) точки \(С\) тоже получаем, опустив перпендикуляр \(CF\) на ось \(OY\). Координата \(y\) \(т.С\) будет равна длине отрезка \(AF=CE\). Найдем его по теореме Пифагора из треугольника \(AFC\): $$ ^2=^2+^2,$$ $$ 4^2=2^2+^2,$$ $$ CE=\sqrt<12>. $$ Координата \(z\) точки \(C\), очевидно, равна \(0\), потому что \(т.С\) лежит в плоскости \(XOY\). $$ C (2;\sqrt<12>; 0). $$

И найдем координаты вершины пирамиды (\(т.D\)). (Рис. 3) Координаты \(X\) и \(Y\) у точки \(D\) совпадают с координатами \(X\) и \(Y\) у точки \(H\). Напомню, что высота правильной треугольной пирамиды падает в точку пересечения медиан, биссектрис и высот. Отрезок \(EH=\frac<1><3>*CE=\frac<1><3>*\sqrt<12>\) (медианы в треугольнике точкой пересечения делятся в отношении как \(\frac<1><3>\)) и равен координате точки \(D\) по \(Y\). Длина отрезка \(IH=2\) будет равна координате точки \(D\) по \(X\). А координата по оси \(Z\) равна высоте пирамиде: $$ ^2=^2+^2, $$ $$ =\sqrt<4^2-<\frac<2><3>*AF>^2>, $$ $$ =\frac<32><3>. $$ $$ D (2, \frac<1><3>*\sqrt<12>, \frac<32><3>). $$

Координаты вектора

Вектор – отрезок, имеющий длину и указывающий направление.

На самом деле, понимать, что такое вектор для решения задач методом координат необязательно. Можно просто использовать это понятие, как необходимый инструмент для решения задач по стереометрии. Любое ребро или отрезок на нашей фигуре мы будем называть вектором.

Для того, чтобы определить координаты вектора, нужно из координат конечной точки вычесть координаты начальной точки. Пусть у нас есть две точки (Рис. 4) : $$ т.А(x_A,y_A,z_A); $$ $$ т.B(x_B,y_B,z_B); $$ Тогда координаты вектора \(\vec\) можно определить по формуле: $$ \vec=. $$

Скрещивающиеся прямые

И так, мы научились находить координаты точек, и при помощи них определять координаты векторов. Теперь познакомимся с формулой нахождения косинуса угла между скрещивающимися прямыми (векторами). Пусть даны два вектора: $$ a=;$$ $$ b=; $$ тогда угол \(\alpha\) между ними находится по формуле: $$ \cos<\alpha>=\frac<\sqrt<^2+^2+^2>*\sqrt<^2+^2+^2>>. $$

Уравнение плоскости

В задачах №14 (С2) ЕГЭ по профильной математике часто требуется найти угол между прямой и плоскостью и расстояние между скрещивающимися прямыми. Но для этого вы должны уметь выводить уравнение плоскости. В общем виде уравнение плоскости задается формулой: $$ A*x+B*y+C*z+D=0,$$ где \(A,B,C,D\) – какие-то числа.

Если найти \(A,B,C,D\), то мы мы найдем уравнений плоскости. Плоскость однозначно задается тремя точками в пространстве, значит нужно найти координаты трех точек, лежащий в данной плоскости, а потом подставить их в общее уравнение плоскости.

Например, пусть даны три точки:

Подставим координаты точек в общее уравнение плоскости:

$$\begin A*x_K+B*y_K+C*z_K+D=0,\\ A*x_L+B*y_L+C*z_L+D=0, \\ A*x_P+B*y_P+C*z_P+D=0.\end$$

Получилась система из трех уравнений, но неизвестных 4: \(A,B,C,D\). Если наша плоскость не проходит через начало координат, то мы можем \(D\) приравнять \(1\), если же проходит, то \(D=0\). Объяснение этому простое: вы можете поделить каждое ваше уравнения на \(D\), от этого уравнение не изменится, но вместо \(D\) будет стоять \(1\), а остальные коэффициенты будут в \(D\) раз меньше.

Теперь у нас есть три уравнения и три неизвестные – можем решить систему:

Найти уравнение плоскости, проходящей через точки $$ K(1;2;3);\,P(0;1;0);\,L(1;1;1). $$ Подставим координаты точек в уравнение плоскости \(D=1\): $$\begin A*1+B*2+C*3+1=0,\\ A*0+B*1+C*0+1=0, \\ A*1+B*1+C*1+1=0.\end$$ $$\begin A+2*B+3*C+1=0,\\ B+1=0, \\ A+B+C+1=0.\end$$ $$\begin A-2+3*C+1=0,\\ B=-1, \\ A=-C.\end$$ $$\begin A=-0.5,\\ B=-1, \\ C=0.5.\end$$ Получаем искомое уравнение плоскости: $$ -0.5x-y+0.5z+1=0.$$

Расстояние от точки до плоскости

Зная координаты некоторой точки \(M(x_M;y_M;z_M)\), легко найти расстояние до плоскости \(Ax+By+Cz+D=0:\) $$ \rho=\frac<|A*x_M+B*y_M+C*z_M+D|><\sqrt>. $$

Найдите расстояние от т. \(H (1;2;0)\) до плоскости, заданной уравнением $$ 2*x+3*y-\sqrt<2>*z+4=0.$$

Из уравнения плоскости сразу находим коэффициенты: $$ A=2,\,B=3,\,C=-\sqrt<2>,\,D=4.$$ Подставим их в формулу для нахождения расстояния от точки до плоскости. $$ \rho=\frac<|2*1+3*2-\sqrt<2>*0+4|><\sqrt<2^2+3^2+<-\sqrt<2>>^2>>. $$ $$ \rho=\frac<12><\sqrt<16>>=3.$$

Расстояние между скрещивающимися прямыми

Расстояние между скрещивающимися прямыми – это расстояние от любой точки одной из прямых до параллельной ей плоскости, проходящей через вторую прямую.

Таким образом, если требуется найти расстояние между скрещивающимися прямыми, то нужно через одну из них провести плоскость параллельно второй прямой. Затем найти уравнение этой плоскости и по формуле расстояния от точки до плоскости найти расстояние между скрещивающимися прямыми. Точку на прямой можно выбрать произвольно (у которой легче всего найти координаты).

Рассмотрим задачу из досрочного ЕГЭ по математике 2018 года.

Дана правильная треугольная призма \(ABCFDE\), ребра которой равны 2. Точка \(G\) — середина ребра \(CE\).

• Докажите, что прямые \(AD\) и \(BG\) перпендикулярны.
• Найдите расстояние между прямыми \(AD\) и \(BG\).

Решим задачу полностью методом координат.

Нарисуем рисунок и выберем декартову систему координат. (Рис 5).