Уравнение расстояния от точки до окружности

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вычисление расстояний между геометрическими объектами

Линейные многообразия

Расстояние от точки до линейного многообразия (плоскости)

Задача. Найти расстояние от точки $ X_ <0>\in <\mathbb R>^ $ до линейного многообразия (плоскости) $ \mathbb M $ в $ <\mathbb R>^ $, заданного системой уравнений $$ \left\< \begin c_<11>x_1+c_<12>x_2+\dots+c_<1n>x_n &=& h_1 \\ \dots & & \dots \\ c_x_1+c_x_2+\dots+c_x_n &=& h_m \end \right. $$ или, в матричном виде $$ CX= <\mathcal H>\quad npu \quad C=\left( \begin c_<11>& c_ <12>& \dots & c_ <1n>\\ \dots & & & \dots \\ c_& c_ & \dots & c_ \end \right)_ ,\ <\mathcal H>=\left( \begin h_1 \\ \vdots \\ h_m \end \right),\ X=\left( \begin x_1 \\ x_2 \\ \vdots \\ x_n \end \right) $$ При этом предполагается, что $ m\le n_<> $ и что ранг матрицы $ C_<> $ равен $ m_<> $, то есть система уравнений совместна и определяемое ею многообразие в $ <\mathbb R>^ $ является $ (n-m)_<> $-мерным.

Теорема 1. [1]. Составим квадратную матрицу порядка $ m+1_<> $:

$$ M=\left( \begin C\cdot C^ <\top>& CX_0- <\mathcal H>\\ (CX_0- <\mathcal H>)^ <\top>& 0 \end \right) $$ Расстояние от точки $ X_ <0>$ до линейного многообразия $ \mathbb M $ вычисляется по формуле $$ d= \sqrt<-\frac<\det M><\det(C\cdot C^<\top>)>> \ . $$

Доказательство ☞ ЗДЕСЬ.

Расстояние от точки $ X_<0>=(x_<10>,\dots,x_)^ <\top>$ до гиперплоскости (или, в случае $ n=2 $, прямой)

$$ c_1x_1+\dots+c_nx_n= h $$ равно $$ d= \frac<|c_1x_<10>+\dots+c_nx_-h|><\sqrt> \ . $$ Ближайшая к $ X_0 $ точка гиперплоскости: $$ X_<\ast>=X_0- \frac+\dots+c_nx_-h> \left(\begin c_1 \\ \vdots \\ c_n \end \right) \, . $$

Пусть теперь линейное многообразие (плоскость) задано параметрически $$ \mathbb M= \ < Y_0+\lambda_1 Y_1+\dots+\lambda_k Y_k \quad \mid \quad \<\lambda_1,\dots,\lambda_k\>\subset <\mathbb R>\> $$ при фиксированных столбцах $$ \\subset <\mathbb R>^n \ . $$ Предположим, что эти столбцы линейно независимы. Составим из них матрицы $$ L=\left[ Y_1|\dots|Y_k \right]_ \quad u \quad \tilde L = \left[ Y_1|\dots|Y_k| X_0-Y_0 \right]_ $$ (здесь $ |_<> $ означает конкатенацию).

Теорема 2. Расстояние $ d_<> $ от точки $ X_ <0>$ до линейного многообразия $ \mathbb M $ вычисляется по формуле

Доказательство. Утверждение теоремы 2 является частным случаем общего результата о вычислении расстояния от точки до линейного многообразия в евклидовом пространстве. ♦

Теорема 3. Ближайшая к точке $ X_0 $ точка многообразия $ \mathbb M_<> $ (проекция точки на многообразие) определяется по формуле

Доказательство ☞ ЗДЕСЬ.

Пример. Найти расстояние от точки $ X_<0>=(1,1,1,1)^ <\top>$ до плоскости

Решение. 1-й способ: применение теоремы 1. Имеем: $$ C=\left( \begin 3 & 1 & -1 & 1 \\ 1 & -2 & 1 & 2 \end \right), <\mathcal H>= \left( \begin 1 \\ 2 \end \right), $$ $$ C\cdot C^ <\top>= \left( \begin 12 & 2 \\ 2 & 10 \end \right),\ CX_0=\left( \begin 4 \\ 2 \end \right), \ CX_0-<\mathcal H>=\left( \begin 3 \\ 0 \end \right) \ , $$ $$ \frac<\left| \begin 12 & 2 & 3 \\ 2 & 10 & 0 \\ 3 & 0 & 0 \end \right|><\left| \begin 12 & 2 \\ 2 & 10 \end \right|>=\frac<-90><116>=-\frac<45> <58>\ . $$

2-й способ: применение теоремы 2. Общее решение системы уравнений, задающей плоскость: $$ x_3=\frac<5><3>x_1+\frac<4><3>x_2, \ x_4=1-\frac<4><3>x_1+\frac<1><3>x_2 \ . $$ Таким образом, плоскость может быть представлена в параметрическом виде $$ Y_0+\lambda_1 Y_1 + \lambda_2 Y_2 \quad npu \quad Y_0 = \left( \begin 0 \\ 0 \\ 0 \\ 1 \end \right),\ Y_1=\left( \begin 0 \\ 3 \\ 4 \\ 1 \end \right),\ Y_2=\left( \begin 3 \\ 0 \\ 5 \\ -4 \end \right) \ . $$ Имеем: $$ L= \left( \begin 0 & 3 \\ 3 & 0 \\ 4 & 5 \\ 1 & -4 \end \right), \ \tilde L =\left( \begin 0 & 3 & 1 \\ 3 & 0 & 1 \\ 4 & 5 & 1 \\ 1 & -4 & 0 \end \right), \ \frac<\left| \begin 26 & 16 & 7 \\ 16 & 50 & 8 \\ 7 & 8 & 3 \end \right|><\left| \begin 26 & 16 \\ 16 & 50 \end \right|>=\frac<810><1044>=\frac<45> <58>\ . $$ Координаты ближайшей точки к $ X_ <0>$: $$ X_<\ast>= \left(\begin 1 \\ 1 \\ 1 \\ 1 \end\right)+\left( \begin 0 & 3 \\ 3 & 0 \\ 4 & 5 \\ 1 & -4 \end \right)\left( \begin 26 & 16 \\ 16 & 50 \\ \end \right)^ <-1>\left(\begin 0 & 3 & 4 & 1 \\ 3 & 0 & 5 & -4 \end \right)\left(\begin 1 \\ 1 \\ 1 \\ 0 \end\right)=\frac<1> <58>\left(\begin 16 \\ 37 \\ 76 \\ 49 \end\right) \, . $$

Ответ. $ d=\sqrt <45/58>\approx 0.8808303295 $.

Расстояние между линейными многообразиями (плоскостями)

Пусть линейные многообразия в $ <\mathbb R>^ $ заданы параметрически $$ \mathbb M_1=\ < X_0+ \lambda_1 X_1+\dots + \lambda_k X_k \ \mid \ \<\lambda_1,\dots,\lambda_k \>\subset \mathbb R \> ; $$ $$ \mathbb M_2=\< Y_0+\mu_1Y_1+\dots+\mu_<\ell>Y_ <\ell>\ \mid \ \ <\mu_1,\dots,\mu_<\ell>\> \subset \mathbb R \> $$ при фиксированных столбцах $$ \\>\subset <\mathbb R>^n . $$ Составим из этих столбцов матрицы $$ P=\left[ X_1|\dots|X_k| Y_1|\dots | Y_ <\ell>\right]_ \quad u \quad \tilde P = \left[ X_1|\dots|X_k| Y_1|\dots | Y_<\ell>| X_0-Y_0 \right]_ $$ (здесь $ |_<> $ означает конкатенацию).

Теорема. Расстояние между линейными многообразиями $ \mathbb M_1 $ и $ \mathbb M_2 $ вычисляется по формуле

Пример. [2]. Найти расстояние между плоскостями

$$ \left( \begin 89 \\ 37 \\ 111 \\ 13 \\54 \end \right) + \lambda_1 \left( \begin 1 \\ 1 \\ 0 \\ -1 \\ -1 \end \right) + \lambda_2 \left( \begin 1 \\ -1 \\ 0 \\ -1 \\ 1 \end \right) \quad \mbox < и >\quad \left( \begin 42 \\ -16 \\ -39 \\ 71 \\3 \end \right) + \mu_1 \left( \begin 1 \\ 1 \\ 0 \\ 1 \\ 1 \end \right) + \mu_2 \left( \begin 1 \\ -1 \\ 0 \\ 1 \\ -1 \end \right) \ . $$

Решение. $$ P^<\top>\cdot P=4\cdot E_<4 \times 4>, \quad \tilde P^<\top>\cdot \tilde P= \left(\begin 4 & 0 & 0 & 0 & 107 \\ 0 & 4 & 0 & 0 & 103 \\ 0 & 0 & 4 & 0 & 93\\ 0 & 0 & 0 & 4 & -115 \\ 107 & 103 & 93 & -115 & 33483 \end \right) \ . $$

Ответ. $ d=150_<> $.

Квадратичные многообразия (квадрики)

В последующих пунктах, касающихся вычисления расстояний между геометрическими объектами, хотя бы один из которых представлен квадратным уравнением, используется следующая идеология решения. Первоначальной целью ставится построение уравнения расстояний, т.е. алгебраического уравнения от одной переменной, среди корней которого находится квадрат искомого расстояния. После нахождения этого корня, координаты ближайшей точки (или пары ближайших точек) находятся в виде рациональных функций от величины квадрата расстояния. Таким образом, мы «переворачиваем» традиционную схему решения оптимизационных задач:

стационарные точки $ \rightarrow $ критические значения

Такая реверсия традиционного подхода оправдана, с одной стороны, тем, что задача сводится к одномерной — поиску корней полинома от одной переменной. Причем нас будет интересовать, как правило, единственный корень этого полинома — минимальный положительный. С другой стороны, уравнение расстояний удается построить в результате чисто алгебраической процедуры: конечного числа элементарных алгебраических операций над коэффициентами уравнений, задающих многообразия. Алгоритм основан на аппарате исключения переменных в системах нелинейных алгебраических уравнений, и ключевым объектом в нем оказывается вычисление дискриминанта полинома (от одной или двух переменных).

Расстояние от точки до квадрики

Теорема 1. Пусть квадрика в $ <\mathbb R>^ $, задана уравнением

$$ X^<\top>AX+2B^<\top>X-1=0 \ , (A=A^<\top>) \ . $$ Квадрат расстояния до нее от не лежащей на ней точки $$ X_ <0>\in <\mathbb R>^, \quad ( X_0^<\top>AX_0+2 B^<\top>X_<0>-1\ne 0 ) $$ равен минимальному положительному корню уравнения расстояний $$ <\mathcal F>(z)=0 \quad npu \quad <\mathcal F>(z)=<\mathcal D>_ <\mu>\left( \Phi(\mu,z) \right) \ . $$ Здесь $$ \Phi(\mu,z)=\det \left( \left[ \begin A & B \\ B^ <\top>& -1 \end \right] + \mu \left[ \begin -E & X_0 \\ X_0^ <\top>& z-X_0^<\top>X_0 \end \right] \right), $$ $ <\mathcal D>_<> $ означает дискриминант полинома $ \Phi(\mu,z) $, рассматриваемого относительно переменной $ \mu_<> $, а $ E_<> $ — единичная матрица порядка $ n_<> $. Дополнительно предполагается, что указанный корень не является кратным.

[3]. Квадрат расстояния от начала координат $ <\mathbb O>\in <\mathbb R>^ $ до квадрики в $ <\mathbb R>^ $, заданной уравнением

$$ X^<\top>AX+2\,B^<\top>X-1=0 \ , $$ равен минимальному положительному корню уравнения расстояний $$ <\mathcal F>(z)=0, \quad npu \quad <\mathcal F>(z)=<\mathcal D>_ <\mu>\left( f(\mu)(\mu z-1)-B^<\top>q(A,\mu)B \right)\ , $$ и при условии, что указанный корень не является кратным. Здесь $ f(\mu_<>)=\det (A-\mu E) $ — характеристический полином матрицы $ A_<> $, а $ q(A,\mu)_<> $ — матрица взаимная матрице $ A-\mu E_<> $.

В частном случае $ B=<\mathbb O>_<> $ (квадрика центрирована к началу координат), имеем:

$$ <\mathcal F>(z)=\left[z^nf(1/z) \right]^2<\mathcal D>_<\mu>(f(\mu)) \ , $$ и расстояние от начала координат до квадрики оказывается равным $ 1/\sqrt<\lambda_<\max>^<>> $, где $ \lambda_<\max>^<> $ — максимальное собственное число матрицы $ A_<> $.

Пример. Найти расстояние от начала координат до эллипсоида

Решение. Здесь $$A = \left( <\begin \frac<7> <18>& -\frac<1> <9>& 0 \\ && \\ -\frac<1> <9>& \frac<1> <3>& -\frac<1> <9>\\ && \\ 0 & -\frac<1> <9>& \frac<5> <18>\end> \right),\quad B = \left( \begin -\frac<1> <12>\\ \\ -\frac<1> <9>\\ \\ \frac<5> <36>\end \right) ,$$ $$ f(\mu)=\det (A-\mu E)=-\mu ^ <3>+ \mu ^ <2>— \frac<11> <36>\mu + \frac <1> <36>$$ Матрица взаимная матрице $ A-\mu E_<> $: $$ q(A, \mu)= \left( \begin \mu ^ <2>— \frac<11> <18>\mu + \frac<13> <162>& — \frac<1> <9>\mu + \frac<5> <162>& \frac<1> <81>\\ && \\ — \frac<1> <9>\mu + \frac<5> <162>& \mu^2 -\frac<2><3>\mu+\frac<35> <324>& — \frac<1> <9>\mu +\frac<7> <162>\\ && \\ \frac<1> <81>& — \frac<1> <9>\mu + \frac<7> <162>& \mu ^ <2>— \frac<13><18>\mu+\frac<19> <162>\end \right) \ . $$ $$ \Phi(\mu,z)=f(\mu)(\mu z-1)-B^<\top>q(A,\mu)B= $$ $$ =-z \mu ^ <4>+ (z+1) \mu ^ <3>+ \left(-\frac <11> <36>z — \frac<673><648>\right) \mu ^ <2>+\left( \frac <1> <36>z + \frac <241> <729>\right) \mu — \frac <1621> <52488>\ . $$ Воспользуемся детерминантным представлением дискриминанта: $$ <\mathcal F>(z) = <\mathcal D>_ <\mu>(\Phi(\mu,z)) = \frac<1> <16>\times $$ $$ \times \left| \begin 4z & — 3z-3 & \frac<11><18>z + \frac<673> <324>& — \frac<1> <36>z — \frac<241> <729>& 0 & 0 \\ &&&&& \\ 0 & 4z & — 3z-3 & \frac<11> <18>z + \frac<673> <324>& — \frac<1> <36>z — \frac<241> <729>& 0 \\ &&&&& \\ 0 & 0 & 4z & — 3z-3 & \frac<11><18>z + \frac<673> <324>& — \frac<1> <36>z — \frac<241> <729>\\ &&&&& \\ 0 & 0 & — z — 1 & \frac<11><18>z + \frac<673> <324>& — \frac<1> <12>z — \frac<241> <243>& \frac<1621> <13122>\\ &&&&& \\ 0 & — z — 1 & \frac<11><18>z + \frac<673> <324>& — \frac<1><12>z — \frac<241> <243>& \frac<1621> <13122>& 0 \\ &&&&& \\ — z — 1 & \frac<11> <18>z + \frac<673> <324>& — \frac<1> <12>z — \frac<241> <243>& \frac<1621> <13122>& 0 & 0 \end \right| = $$ $$ =2^<-11>3^ <-24>( 38263752\,z^6-966487788\,z^5+9376985736\,z^4-43882396481\,z^3+$$ $$ +102982092872\,z^2-116747905827\,z+50898162294) \quad . $$ Вещественные корни уравнения расстояний: $$ z_1\approx 1.394685, \ z_2 \approx 5.701814, \ z_3 \approx 7.043941,\ z_4 \approx 7.590060 \ . $$

Ответ. $ d= \sqrt \approx 1.180968 $.

Нахождение точки на квадрике, ближайшей к заданной точке $ X_ <0>$, возможно с помощью следующего результата.

Теорема 2. При выполнении условий теоремы 1, координаты точки $ X_ <\ast>$ квадрики, ближайшей к точке $ X_ <0>$ находятся по формуле

$$ X_<\ast>=-A^ <-1>B — \mu_ <\ast>(A -\mu_<\ast>E)^ <-1>(A^ <-1>B+X_0)=(\mu_<\ast>E- A)^ <-1>(B+\mu_ <\ast>X_0)\ . $$ Здесь $ \mu_ <\ast>$ означает кратный корень полинома $ \Phi(\mu,z_<\ast>) $, где полином $ \Phi(\mu,z) $ берется из формулировки теоремы 1, а $ z_<\ast>^<> $ означает минимальный положительный корень уравнения расстояний.

Этот результат требует пояснений. Итак, поскольку дискриминант полинома $ \Phi(\mu,z_<\ast>) $ обращается в нуль, то у этого полинома — как полинома по $ \mu_<> $ — имеется кратный корень $ \mu =\mu_ <\ast>$. Можно доказать [4], что при условии простоты корня $ z=z_ <\ast>$ уравнения расстояний $ \mathcal F(z)=0 $ кратность корня $ \mu =\mu_ <\ast>$ для полинома $ \Phi(\mu,z_<\ast>) $ будет равна ровно $ 2_<> $, и других кратных корней этот полином не имеет. Но тогда, выражение для $ \mu_<\ast>^<> $ может быть найдено в виде рациональной функции коэффициентов полинома $ \Phi(\mu,z_<\ast>) $. Последнее утверждение может быть доказано разными способами, и в качестве самого наглядного выберем тот, что основан на свойствах дискриминанта, например, на том, что изложено ☞ ЗДЕСЬ.

При выполнении условия предыдущей теоремы, координаты точки $ X_<\ast>^<> $, ближайшей на квадрике к точке $ X_ <0>$, являются рациональными функциями от квадрата расстояния.

Точка $ X_ <\ast>$ квадрики $ X^<\top>AX+2\,B^<\top>X-1=0 $, ближайшая к началу координат $ X_0= \mathbb O $, находится по формуле:

$$ X_ <\ast>= — \frac<1>)> q(A,\mu_<\ast>) B \ . $$ Здесь $ f(\mu_<>)=\det (A-\mu E) $ — характеристический полином матрицы $ A_<> $, $ q(A,\mu)_<> $ — матрица взаимная матрице $ A-\mu E_<> $, а $ \mu_ <\ast>$ означает кратный корень уравнения $$f(\mu)(\mu z_<\ast>-1)-B^<\top>q(A,\mu)B=0 , $$ где $ z_<\ast>^<> $ — величина квадрата расстояния от $ \mathbb O_<> $ до квадрики.

Пример. Найти ближайшую к началу координат точку эллипсоида из предыдущего примера.

Решение. Подставляем $ z_<>=z_ <\ast>\approx 1.394685 $ в формулу для определения кратного корня, т.е. в отношение двух конкретных миноров детерминантного представления дискриминанта: $$ \mu=-\frac<\left| \begin 4z & — 3z-3 & \frac<11> <18>z + \frac<673> <324>& 0 \\ &&& \\ 0 & 4z & — 3z-3 & — \frac<1> <36>z — \frac<241> <729>\\ &&& \\ 0 & — z — 1 & \frac<11><18>z + \frac<673> <324>& \frac<1621> <13122>\\ &&& \\ — z — 1 & \frac<11><18>z + \frac<673> <324>& — \frac<1><12>z — \frac<241> <243>& 0 \end \right|> <\left| \begin 4z & — 3z-3 & \frac<11> <18>z + \frac<673> <324>& — \frac<1> <36>z — \frac<241> <729>\\ &&& \\ 0 & 4z & — 3z-3 & \frac<11><18>z + \frac<673> <324>\\ &&& \\ 0 & — z — 1 & \frac<11><18>z + \frac<673> <324>& — \frac<1><12>z — \frac<241> <243>\\ &&& \\ — z — 1 & \frac<11><18>z + \frac<673> <324>& — \frac<1><12>z — \frac<241> <243>& \frac<1621> <13122>\end \right|> $$ получаем $ \mu_<\ast>^<> \approx 0.572670 $. Подставляем это значение в формулу для определения $ X_<\ast>^<> $ из последнего следствия: $$ X_<\ast>\approx \left(\begin 0.071171 \\ -0.867719 \\ 0.797924 \end \right) \ . $$

Проверка. Если подставить вместо $ X_ <\ast>$ его приближенное значение, то получим: $$ X_<\ast>^ <\top>X_ <\ast>\approx \mathbf<1.39468>4,\ X_<\ast>^<\top>AX_<\ast>+2\,B^<\top>X_<\ast>-1 \approx 2.9\cdot 10^<-5>\ , $$ и вектор $ <\mathbb O>X_ <\ast>$ перпендикулярен эллипсоиду в точке $ X_<>=X_ <\ast>$: $$ AX_<\ast>+B \approx \left(\begin 0.040757\\ -0.496917 \\ 0.456948 \end \right)\approx \mu_ <\ast>X_ <\ast>\ . $$

Расстояние от линейного многообразия (плоскости) до квадрики

Задача. Найти расстояние от эллипсоида в $ <\mathbb R>^ $, заданного уравнением $$ X^<\top>AX+2B^<\top>X-1=0 \ , (A=A^<\top>) $$ до линейного многообразия (плоскости) в $ <\mathbb R>^ $, заданной системой уравнений $$ \left\< \begin c_<11>x_1+c_<12>x_2+\dots+c_<1n>x_n &=& 0 \\ \dots & & \dots \\ c_x_1+c_x_2+\dots+c_x_n &=& 0 \end \right. \ \iff \ CX= <\mathbb O>\quad npu \quad C=\left( \begin c_<11>& c_ <12>& \dots & c_ <1n>\\ \dots & & & \dots \\ c_& c_ & \dots & c_ \end \right)_ $$ При этом предполагается, что $ m\le n_<> $ и что ранг матрицы $ C_<> $ равен $ m_<> $, т.е. определяемая системой плоскость в $ <\mathbb R>^ $ является $ (n-m)_<> $-мерной.

Теорема. [3]. Необходимое и достаточное условие того, что линейное многообразие (плоскость) пересекает эллипсоид зависит от знакоопределенности матрицы $ A_<> $:

Условие равенства нулю определителя из теоремы является необходимым и достаточным для существования точки касания эллипсоида и плоскости.

Теорема. [3]. Если условие предыдущей теоремы не выполняется, то квадрат расстояния от эллипсоида до плоскости совпадает с минимальным положительным корнем полинома

$$ <\mathcal F>(z) =<\mathcal D>_\mu \left( \mu^m \left| \begin A & B & C^<\top>\\ B^ <\top>& -1 + \mu z & \mathbb\\ C & \mathbb & \frac<1> <\mu>C \cdot C^ <\top>\end \right| \right), $$ в предположении, что этот корень не является кратным. Здесь $ <\mathcal D>_<> $ — дискриминант полинома, рассматриваемого относительно переменной $ \mu_<> $.

Если строки матрицы $ C_<> $ ортонормированны, то преобразованием определителя в теореме можно понизить его порядок: выражение под знаком дискриминанта можно преобразовать в

Пример. Найти расстояние от оси $ <\mathbb O>x_ <1>$ до эллипсоида

$$ 7\, x_1^2+6\, x_2^2 +5\, x_3^2 -4\,x_1x_2-4\,x_2x_3-37\,x_1-12\,x_2+3\,x_3+54=0 \ . $$

Решение. Здесь $$ A= \left( \begin -\frac<7> <54>& \frac<1> <27>& 0 \\ &&\\ \frac<1> <27>& -\frac<1> <9>& \frac<1> <27>\\ &&\\ 0 & \frac<1> <27>& -\frac<5> <54>\end \right), \ B=\left( \begin \frac<37> <108>\\ \\ \frac<1> <9>\\ \\ -\frac<1> <36>\end \right) $$ и можно взять $$ C= \left( \begin 0 & 1 & 0 \\ 0 & 0 & 1 \end \right) \ . $$ Матрица $ A_<> $ отрицательно определена, условие пересечения прямой и эллипсоида не выполняется: $$ \left| \begin A & B & C^<\top>\\ B^ <\top>& -1 & <\mathbb O>\\ C & <\mathbb O>& \mathbb \end \right| \times (-1)^3 = — \frac <143>

Расстояния в $ <\mathbb R>^ $ от плоскости

$$ c_1x_1+\dots+c_nx_n = h \ \iff \ CX=h $$ до ближайшей и до самой дальней точек эллипсоида $$ X^<\top>AX+2B^<\top>X-1=0 \ , (A=A^<\top>) $$ совпадают с модулями корней полинома: $$ <\mathcal F>(Z)=\left| \begin A & B & C^<\top>/|C|\\ B^ <\top>& -1 & Z-h/|C|\\ C/|C| & Z-h/|C| & 0 \end \right| \ . $$ Здесь $ |C|=\sqrt> $ и предполагается, что поверхности не пересекаются.

Пример. Найти расстояние от прямой $ 2\, x_1- x_<2>=0 $ до эллипса

$$ 7\,x_1^2-4\,x_1x_2 + 6\, x_2^2-47\, x_1 -24\, x_ <2>+124 = 0 .$$

Решение. Здесь $$ <\mathcal F>(Z)=\left| \begin A & B & C^<\top>/|C| \\ B^ <\top>& -1 & Z-h/|C| \\ C/|C| & Z-h/|C| & 0 \end \right| = \left| \begin -\frac<7> <124>& \frac<1> <62>& \frac<47> <248>& \frac<2><\sqrt<5>> \\ &&& \\ \frac<1> <62>& — \frac<3> <62>& \frac<3> <31>&- \frac<1><\sqrt<5>> \\ &&& \\ \frac<47> <248>& \frac<3> <31>& -1 & Z \\ &&& \\ \frac<2><\sqrt<5>> & — \frac<1><\sqrt<5>> & Z & 0 \end \right| = $$ $$ =-\frac<1><307520>\left(760\,Z^2+1592\sqrt<5>\, Z+2383 \right) $$ и корни этого полинома: $$ -\frac<199><190>\sqrt<5>\pm \frac<1> <76>\sqrt <13570>\ . $$

Ответ. $$ d = \left| -\frac<199><190>\sqrt<5>+ \frac<1> <76>\sqrt <13570>\right| \approx 0.809219_<> \ . $$

Расстояние между квадриками

Теорема. Пусть $ X^ <\top>A_ <1>X =1 $ и $ X^ <\top>A_ <2>X =1 $ – квадрики в $ <\mathbb R>^ $, причем первая является эллипсоидом. Квадрики не пересекаются тогда и только тогда, когда матрица $ A_<1>-A_2 $ является знакоопределенной.

Доказательство ☞ ЗДЕСЬ.

Теорема. [3,4]. Если выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ \mbox <эллипсоидом>\ X^ <\top>A_ <1>X =1\ \mbox<и квадрикой>\ X^ <\top>A_ <2>X =1 $$ совпадает с минимальным положительным корнем уравнения расстояний $$ <\mathcal F>(z)=0 \quad npu \quad <\mathcal F>(z)=<\mathcal D>_ <\lambda>\left( \Phi(\lambda,z) \right) \ . $$ Здесь $$ \Phi(\lambda,z)=\det (\lambda A_1 + (z- \lambda) A_2 — \lambda (z-\lambda) A_1 A_2), $$ $ <\mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменной $ \lambda_<> $. Дополнительно предполагается, что указанный корень не является кратным.

Пример. Найти расстояние между эллипсами

$$10\,x_1^2-12\,x_1x_2+8\,x_2^2=1 \qquad u \qquad x_1^2+x_1x_2+x_2^2=1 \ . $$

Решение. Здесь $$ A_1= \left( \begin 10 & — 6 \\ -6 & 8 \end \right), \quad A_2= \left( \begin 1 & \frac<1> <2>\\ \frac<1> <2>& 1 \end \right) $$ и матрица $ A_<1>-A_2 $ положительно определена. Следовательно эллипсы не пересекаются. $$ \Phi(\lambda,z)=\det (\lambda A_1 + (z- \lambda) A_2 — \lambda (z-\lambda) A_1 A_2)= $$ $$ =33\,\lambda^4+\left(-66z+\frac<149><2>\right)\lambda^3+\left(33\,z^2-61\,z+\frac<83><4>\right)\lambda^2+\left(-\frac<27><2>z^2+\frac<45><2>z\right)\lambda+\frac<3><4>\,z^2 $$ и дискриминант этого полинома по переменной $ \lambda_<> $ равен $$ <\mathcal F>(z)=\frac<3><16>z^2 (<\scriptstyle 936086976>\, z^6-<\scriptstyle 10969697376>\,z^5+ <\scriptstyle 50706209664>\, z^4 —<\scriptstyle 115515184664>\, z^3+<\scriptstyle 130176444432>\, z^2 —<\scriptstyle 59826725574>\,z+<\scriptstyle 2866271785>) \ . $$ Положительные корни уравнения расстояний $ <\mathcal F>(z)=0 $: $$ z_1 \approx 0.053945666,\ z_2 \approx 1.3340583883,\ z_3 \approx 1.95921364,\ z_4 \approx 2.8785867381 \ . $$

Ответ. $ d_<>= \sqrt \approx 0.23226206 $.

Нахождение координат ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по алгоритму:

1. Если $ z=z_ <\ast>$ — корень полинома $ <\mathcal F>(z) $, то это значит, что полином $$ \Phi(\lambda, z_<\ast>) = \det ( \lambda A_1 +(z_<\ast>-\lambda)A_2 — \lambda (z_<\ast>-\lambda) A_2A_1) $$ имеет кратный корень $ \lambda_<> = \lambda_ <\ast>$. При выполнении условий теоремы, этот корень будет единственным второй кратности и его можно выразить в виде рациональной функции от $ z_ <\ast>$ с помощью субдискриминантов.

2. Столбец координат $ X_<\ast>^<> $ точки первой квадрики, удовлетворяет тогда однородной системе уравнений $$ ( \lambda_ <\ast>A_1 +(z_<\ast>-\lambda_<\ast>)A_2 — \lambda_ <\ast>(z_<\ast>-\lambda_<\ast>) A_2A_1) X = \mathbb O \ , $$ которая имеет бесконечное множество решений, поскольку определитель ее матрицы равен нулю. Из этого бесконечного множества мы выделяем те решения, что удовлетворяют условию $ X^<\top>A_<1>X=1 $.

При выполнении условий теоремы таких решений будет два (что соответствует симметрии задачи, см. рисунок).

Аналогично, столбец координат $ Y_<\ast>^<> $ точки на второй квадрике $ Y^<\top>A_<2>Y=1_<> $ будет решением системы уравнений $$ ( \lambda_ <\ast>A_1 +(z_<\ast>-\lambda_<\ast>)A_2 — \lambda_ <\ast>(z_<\ast>-\lambda_<\ast>) A_1A_2) Y = \mathbb O \ . $$

Для нахождения решений воспользуемся одним из результатов теории систем линейных уравнений. Составим столбец из алгебраических дополнений к элементам какой-либо строки матрицы $$ M= \lambda_ <\ast>A_1 +(z_<\ast>-\lambda_<\ast>)A_2 — \lambda_ <\ast>(z_<\ast>-\lambda_<\ast>) A_2A_1 \ . $$ Тогда вектор $ X_<\ast>^<> $ отличается от этого столбца лишь множителем, который определится из условия $ X^<\top>A_<1>X=1_<> $. Аналогично, для получения столбца координат $ Y_<\ast>^<> $ возьмем столбец из алгебраических дополнений к элементам какого-либо столбца той же матрицы $ M_<> $ и домножим его на константу, чтобы обеспечить выполнение условия $ Y^<\top>A_<2>Y=1_<> $.

3. Получившиеся пары $ X_<\ast>,Y_<\ast>^<> $ надо согласовать: они должны подчиняться условию $$ (X_<\ast>-Y_<\ast>)^<\top>(X_<\ast>-Y_<\ast>)=z_ <\ast>\ . $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Решение. Для найденного значения $ z_<\ast>=z_1 \approx 0.053945666_<> $ определитель матрицы $$ M=\left( \begin 7\,\lambda^2+(-7z+9)\lambda+z & -2\lambda^2+(2\,z-\frac<13><2>)\lambda+\frac<1><2>z \\ & \\ -\lambda^2+(z-\frac<13><2>)\lambda+\frac<1><2>z & 5\lambda^2+(-5z+7)\lambda+z \end \right) $$ как полином по $ \lambda_<> $ будет иметь кратный корень. Этот корень определяем 1) с помощью субдискриминантов в виде: $$ \lambda=-\frac<-725274\,z^5+1455894\,z^4+\frac<11286981><2>z^3-\frac<26486523><2>z^2+\frac<42000075><8>z> <17591706\,z^4-109992894\,z^3+\frac<450450691><2>z^2-\frac<315606253><2>z+\frac<77466805><8>> \ . $$ Подстановка сюда $ z=z_<\ast>^<> $ даст $ \lambda_ <\ast>\approx -0.13576051_<> $.

Далее, при найденных значениях $ z_<> $ и $ \lambda_<> $ система линейных уравнений $$ MX=\mathbb O_ <2\times 1>$$ должна иметь бесконечное множество решений относительно вектора $ X_<2\times 1>^<> $. Одно из этих решений может быть построено (см. упражнение ☞ ЗДЕСЬ ) с помощью алгебраических дополнений к элементам, например, второй строки матрицы $ M_<> $: $$ \left( \begin 2\lambda^2-(2\,z-\frac<13><2>)\lambda-\frac<1><2>z \\ \\ 7\,\lambda^2+(-7z+9)\lambda+z \end \right) \quad \begin \longrightarrow \\ z=z_<\ast>, \lambda= \lambda_ <\ast>\end \quad X=\left( \begin -0.8579069 \\ \\ -0.9876166 \end \right) \ . $$ Любое другое решение получается домножением полученного на произвольную константу («растяжением» вектора). Воспользуемся этим, чтобы добиться выполнения условия $ X^<\top>A_ <1>X =1_<> $. $$ X_<\ast>=\frac<1><\sqrtA_1 X>> X \approx \left( \begin -0.3838312 \\ -0.4418639 \end \right) \ . $$ Аналогично, для нахождения точки на другом эллипсе, мы решаем систему $$ M^<\top>Y=\mathbb O_ <2\times 1>\ , $$ представив ее решение опять-таки с помощью алгебраических дополнений к элементам второго столбца матрицы $ M_<> $: $$ \left( \begin \lambda^2-(z-\frac<13><2>)\lambda-\frac<1><2>z \\ \\ 7\,\lambda^2+(-7z+9)\lambda+z \end \right) \quad \begin \longrightarrow \\ z=z_<\ast>, \lambda= \lambda_ <\ast>\end \quad \left( \begin -0.8836615 \\ \\ -0.9876166 \end \right) \quad \Rightarrow \quad Y_ <\ast>\approx \left( \begin -0.5449964 \\ \\ -0.6091105 \end \right) \ . $$

Ответ. $ \pm (0.3838312,\, 0.4418639)_<> $ и $ \pm (0.5449964,\, 0.6091105)_<> $ соответственно (знаки должны быть согласованы).

Проверка. Если в ответе взять знак $ +_<> $: $$ X_<\ast>-Y_ <\ast>= \left( \begin -0.1611652 \\ -0.1672466 \end \right)= \lambda_ <\ast>A_1X_<\ast>=(\lambda_<\ast>-z_<\ast>)A_2Y_<\ast>,\quad (X_<\ast>-Y_<\ast>)^<\top>(X_<\ast>-Y_<\ast>)\approx \mathbf<0.0539456>4 \ . $$

Теорема. [3,4].Пусть

$$ X^ <\top>A_<1>X+2\,B^<\top>_1X-1=0 \ \mbox <и>\ X^ <\top>A_<2>X+2\,B^<\top>_2X-1=0 $$ — квадрики в $ <\mathbb R>^_<> $, причем первая является эллипсоидом. Квадрики пересекаются тогда и только тогда, когда среди вещественных корней полинома

$$ \Theta (z) = <\mathcal D>_\lambda \left( \det \left( \left[ \begin A_2 & B_2\\ B_2^ <\top>& -1-z \end \right] — \lambda \left[ \begin A_1 & B_1\\ B_1^ <\top>& -1 \end \right] \right) \right) $$ имеются числа разных знаков или нуль. Здесь $ <\mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменной $ \lambda_<> $.

Для того, чтобы существовала точка касания квадрик

$$ X^ <\top>A_<1>X+2\,B^<\top>_1X-1=0 \ \mbox <и>\ X^ <\top>A_<2>X+2\,B^<\top>_2X-1=0 $$ необходимо и достаточно, чтобы было выполнено условие $$ <\mathcal D>_\lambda \left( \det \left( \left[ \begin A_2 & B_2\\ B_2^ <\top>& -1 \end \right] — \lambda \left[ \begin A_1 & B_1\\ B_1^ <\top>& -1 \end \right] \right) \right) =0 \ . $$

Теорема. [3,4]. Если не выполняется условие предыдущей теоремы, то квадрат расстояния между

$$ \mbox <эллипсоидом>\quad X^ <\top>A_<1>X+2\,B^<\top>_1X-1=0 \quad \mbox < и квадрикой >\quad X^ <\top>A_<2>X+2\,B^<\top>_2X-1=0 $$ совпадает с минимальным положительным корнем полинома $$ <\mathcal F>(z) = $$ $$ =<\mathcal D>_ <\mu_1, \mu_2>\left( \det \left( \mu_1 \left[ \begin A_1 & B_1\\ B_1^ <\top>& -1 \end \right] + \mu_2 \left[ \begin A_2 & B_2\\ B_2^ <\top>& -1 \end \right] — \left[ \begin A_2 A_1 & A_2 B_1\\ B_2^ <\top>A_1 & B_2^<\top>B_1 — \mu_1 \mu_2 z \end \right] \right) \right), $$ в предположении, что этот корень не является кратным. Здесь $ <\mathcal D>_<> $ — дискриминант полинома рассматриваемого относительно переменных $ \mu_<1>, \mu_ <2>$.

Пример. Найти расстояние между эллипсами

Ответ. $ d \approx \sqrt <9.0183982802>\approx 3.00306481 $.

Нахождение ближайших точек на квадриках (обеспечивающих найденное расстояние) возможно по следующему алгоритму.

2. Составим матрицу $$ M= \mu_ <1\ast>A_1+\mu_<2\ast>A_2-A_2A_1 \ . $$ Тогда координатные столбцы ближайших точек на квадриках вычисляются по формулам: $$ X_<\ast>=M^ <-1>(A_2B_1-\mu_ <1\ast>B_1-\mu_<2\ast>B_2),\ Y_<\ast>=(M^<-1>)^<^<\top>> (A_1B_2 — \mu_ <1\ast>B_1-\mu_<2\ast>B_2). $$

Пример. Найти ближайшие точки эллипсов из предыдущего примера.

Ответ. $$ X_<\ast>\approx \left(\begin -0.4824707833 \\ 1.1065143947 \end \right),\ Y_<\ast>\approx \left( \begin -3.46262940675\\ 0.73630788509 \end \right)\ . $$

Проверка. $$ (X_<\ast>-Y_<\ast>)^<\top>(X_<\ast>-Y_<\ast>)\approx \mathbf<9.018398280>3\ , $$ $$ X_<\ast>^<\top>A_1X_<\ast>+2B_1^<\top>X_<\ast>-1 \approx 1\cdot 10^<-9>\ , \ Y_<\ast>^<\top>A_2Y_<\ast>+2B_2^<\top>Y_<\ast>-1\approx -3\cdot 10^<-10>\ , $$ и вектор $ X_<\ast>-Y_<\ast>^<> $ перпендикулярен обоим эллипсам в соответствующих ближайших точках: $$ A_1X_<\ast>+B_1= \left(\begin 1.767863990 \\ 0.219610712 \end \right)=\mu_ <2\ast>(X_<\ast>-Y_<\ast>), \ A_2Y_<\ast>+B_2= \left(\begin -0.1254448880 \\ -0.0155832356 \end \right)=-\mu_ <1\ast>(X_<\ast>-Y_<\ast>) \ . $$

Пример. Найти расстояние между эллипсоидами

$$ 7\,x_1^2+6\,x_2^2+5\,x_3^2-4\,x_1x_2-4\,x_2x_3-37\,x_1-12\,x_2+3\,x_3+54=0$$ и $$ 189\,x_1^2+x_2^2+189\,x_3^2+2\,x_1x_3-x_2x_3-27=0\ .$$

Ответ. $ d \approx \sqrt <1.3537785005>\approx 1.1635198754_<> $

Алгебраические кривые и многообразия

Расстояние от точки до плоской алгебраической кривой

Задача. Пусть алгебраическая кривая задана уравнением $$ \Phi(x,y)=0 \ . $$ Здесь $ \Phi_<>(x,y) $ — отличный от константы полином от $ x_<> $ и $ y_<> $ с вещественными коэффициентами. Требуется найти расстояние до этой кривой от начала координат.

Здесь возникает проблема, которую для рассмотренных выше случаев удавалось либо обойти, либо же сравнительно дешево решить: это проблема существования решения. Дело в том, что уравнение может не иметь вещественных решений, то есть не определять никакой кривой на плоскости $ \mathbb R^ <2>$.

Будем решать задачу сначала для частного случая — пусть полином $ \Phi_<>(x,y) $ является четным по переменной $ y_<> $. Геометрически это означает, что кривая (если она существует) будет зеркально симметричной относительно оси $ \mathbb Ox $. А с аналитической точки зрения такой полином можно представить в виде полинома $$ F(x,Y) \equiv \Phi_<>(x,y) \quad npu \quad Y=y^2 \ . $$

Теорема 1 [6]. Пусть $ \Phi_<>(x,y) \equiv \Phi_<>(x,-y) $. Уравнение $ \Phi_<>(x,y)=0 $ не имеет вещественных решений если одновременно выполняются два условия:

a) уравнение $ \Phi(x,0)=0 $ не имеет вещественных решений;

б) уравнение $$ \mathcal F(z)=\mathcal D_x( F(x,z-x^2))=0 $$ не имеет положительных решений.

Если хотя бы одно из этих условий не выполняется, то квадрат расстояния от начала координат до кривой $ \Phi(x_<>,y)=0 $ равен либо квадрату минимального по модулю вещественного корня уравнения $ \Phi(x,0)=0 $, либо же минимальному положительному корню уравнения $ \mathcal F(z)= 0 $, при условии, что последний не является кратным. Здесь $ <\mathcal D>_<> $ — дискриминант полинома, рассматриваемого относительно переменной $ x_<> $.

Пример. Найти расстояние от начала координат до кривой

Решение. Уравнение $$ \Phi(x,0)=x^6-6\,x^5+25\,x-45=0 $$ имеет вещественные корни $ \mu_1\approx -1.621919 $ и $ \mu_2 \approx 5.986387 $. Далее, $$ F(x,Y)=x^6-5\,x^4Y-Y^3-6\,x^5+6\,xY^2+10\,Y^2+25\,x-45 $$ и полином $$ \mathcal F(z)=\mathcal D_x (F(x,z-x^2))= <\scriptstyle 124422592>\,z^<15>—<\scriptstyle 1996675968>z^<14>—<\scriptstyle 26107738048>\,z^<13>+<\scriptstyle 270691240064>\,z^<12>+ <\scriptstyle 1462429768576>z^ <11>$$ $$ —<\scriptstyle 31070151855680>z^<10>+ <\scriptstyle 104850679100160>\,z^9+<\scriptstyle 106422502370800>\,z^8-<\scriptstyle 1956603249193600>\,z^7+<\scriptstyle 1683409252901600>\,z^6+ $$ $$ +<\scriptstyle 3565828983027500>z^5 —<\scriptstyle 23058839076745500>\,z^4+<\scriptstyle 30272455856370000>\,z^3+<\scriptstyle 28139412928130000>\,z^2-<\scriptstyle 97452805338000000>\, z+ $$ $$ + <\scriptstyle 171049864407603125>$$ имеет минимальный положительный корень равный $ \lambda \approx 1.965293 $. Поскольку $ \sqrt <\lambda>4) , задача о трёх заводах.

Пример. В точках $ P_<1>,P_2,P_3 $ расположены источники полезных ископаемых: железной руды, угля и воды соответственно. Известно, что для производства одной тонны стали необходимо иметь $ m_ <1>$ тонн руды, $ m_2 $ тонн угля и $ m_3 $ тонн воды. В предположении, что стоимость перевозки одной тонны груза не зависит от его природы, где следует расположить сталелитейное производство так, чтобы минимизировать транспортные издержки?

Подробное обсуждение этой задачи (и к ней примыкающих) ☞ ЗДЕСЬ.

Задача о точке Лемуана-Греба

Задача. Найти точку плоскости, cумма квадратов расстояний от которой до сторон треугольника, лежащего в этой же плоскости, минимальна.

Решение. Пусть $ d_1, d_2,d_3 $ — расстояния от точки $ P_<> $ плоскости до сторон треугольника с длинами $ D_1, D_2, D_3 $ соответственно. Воспользуемся тождеством Лагранжа: $$ (d_1^2+ d_2^2+d_3^2)(D_1^2+ D_2^2+D_3^2)\equiv $$ $$ \equiv (d_1D_1+ d_2D_2+d_3D_3)^2+(d_1D_2-d_2D_1)^2+(d_2D_3-d_3D_2)^2+ (d_1D_3-d_3D_1)^2 \ . $$ Величина $ d_1D_1+ d_2D_2+d_3D_3 $ является постоянной, не зависящей от координат точки $ P_<> $: $$ d_1D_1+ d_2D_2+d_3D_3 =2S \ , $$ где $ S_<> $ — площадь данного треугольника. Следовательно $ \min (d_1^2+d_2^2+d_3^2) $ достигается при условиях $$ d_1D_2-d_2D_1=0,\ d_2D_3-d_3D_2=0,\ d_1D_3-d_3D_1=0 \ , $$ то есть когда $$ \frac=\frac=\frac \ . $$ Определяемая этими соотношениями точка называется точкой Лемуана 6) или точкой Греба 7) ; в ней пересекаются симедианы треугольника.

Еще некоторые задачи

Построение прямой на плоскости, сумма квадратов расстояний до которой от заданных точек минимальна ☞ ЗДЕСЬ

Наименьшее расстояние между точкой и окружностью

Данный круг с данным радиусом имеет свой центр в определенной позиции в координатной плоскости. В координатной плоскости задается другая точка. Задача — найти кратчайшее расстояние между точкой и окружностью.

Примеры:

Подход :

так,

Ниже приведена реализация вышеуказанного подхода:

// C ++ программа для поиска
// Наименьшее расстояние
// между точкой и
// круг
#include

using namespace std;

// Функция для поиска кратчайшего расстояния

void dist( double x1, double y1, double x2, double y2, double r)

cout «The shortest distance «

«between a point and a circle is «

sqrt (( pow ((x2 — x1), 2))

double x1 = 4, y1 = 6,

x2 = 35, y2 = 42, r = 5;

dist(x1, y1, x2, y2, r);

// Java-программа для поиска
// Наименьшее расстояние
// между точкой и
// круг

// Функция для поиска кратчайшего расстояния

static void dist( double x1, double y1, double x2,

double y2, double r)

System.out.println( «The shortest distance «

+ «between a point and a circle is «

+ (Math.sqrt((Math.pow((x2 — x1), 2 ))

+ (Math.pow((y2 — y1), 2 )))

public static void main(String[] args)

double x1 = 4 , y1 = 6 ,

x2 = 35 , y2 = 42 , r = 5 ;

dist(x1, y1, x2, y2, r);

/ * Этот код предоставлен PrinciRaj1992 * /

# Python программа для поиска
# Наименьшее расстояние
# между точкой и
# круг

# Функция поиска кратчайшего расстояния

def dist(x1, y1, x2, y2, r):

print ( «The shortest distance between a point and a circle is «

,((((x2 — x1) * * 2 ) + ((y2 — y1) * * 2 )) * * ( 1 / 2 )) — r);

dist(x1, y1, x2, y2, r);

# Этот код предоставлен 29AjayKumar

// C # программа для поиска кратчайшего расстояния
// между точкой и окружностью

// Функция для поиска кратчайшего расстояния

static void dist( double x1, double y1, double x2,

double y2, double r)

Console.WriteLine( «The shortest distance «

+ «between a point and a circle is «

+ (Math.Sqrt((Math.Pow((x2 — x1), 2))

+ (Math.Pow((y2 — y1), 2)))

public static void Main(String[] args)

double x1 = 4, y1 = 6,

x2 = 35, y2 = 42, r = 5;

dist(x1, y1, x2, y2, r);

/ * Этот код предоставлен PrinciRaj1992 * /

// PHP программа для поиска
// Наименьшее расстояние
// между точкой и
// круг

// Функция для поиска кратчайшего расстояния

function dist( $x1 , $y1 , $x2 , $y2 , $r )

echo «The shortest distance between a point and a circle is «

Вычислительная геометрия, или как я стал заниматься олимпиадным программированием. Часть 2

Вступление

Это вторая часть моей статьи посвящена вычислительной геометрии. Думаю, эта статья будет интереснее предыдущей, поскольку задачки будут чуть сложнее.

Начнем с взаимного расположения точки относительно прямой, луча и отрезка.

Задача №1

Определить взаимное расположении точки и прямой: лежит выше прямой, на прямой, под прямой.

Решение
Понятно, что если прямая задана своим уравнением ax + by + c = 0, то тут и решать нечего. Достаточно подставить координаты точки в уравнение прямой и проверить чему оно равно. Если больше нуля, то точка находится в верхней полуплоскости, если равна нулю, то точка находится на прямой и если меньше нуля, то точка находится в нижней полуплоскости. Интереснее случай, когда прямая задана, задана координатами двух точек назовем их P₁(x₁, y₁), P₂(x₂, y₂). В этом случае можно спокойно найти коэффициенты a, b и c и применить предыдущее рассуждение. Но надо сначала подумать, оно нам надо? Конечно, нет! Как я говорил косое произведения — это просто жемчужина вычислительной геометрии. Давайте применим его. Известно, что косое произведение двух векторов положительно, если поворот от первого вектора ко второму идет против часовой стрелки, равно нулю, если векторы коллинеарны и отрицательно, если поворот идет по часовой стрелки. Поэтому нам достаточно посчитать косое произведение векторов P₁P₂ и P₁M и по его знаку сделать вывод.

Задача №2

Определить принадлежит ли точка лучу.

Решение
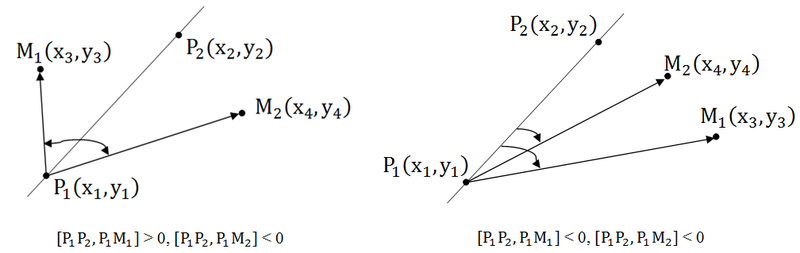
Давайте вспомним, что такое луч: луч — это прямая, ограниченная точкой с одной стороны, а с другой стороны бесконечная. То есть луч задается некоторой начальной точкой и любой точкой лежащей на нем. Пусть точка P₁(x₁, y₁) — начало луча, а P₂(x₂, y₂) — любая точка принадлежащая лучу. Понятно, что если точка принадлежит лучу, то она принадлежит и прямой проходящей через эти точки, но не наоборот. Поэтому принадлежность прямой является необходимым, но не достаточным условием для принадлежности лучу. Поэтому от проверки косового произведения нам никуда не деться. Для достаточного условия нужно вычислить еще и скалярное произведение тех же векторов. Если оно меньше нуля, то точка не принадлежит лучу, если же оно не отрицательно, то точка лежит на луче. Почему так? Давайте посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на луче с начальной точкой P₁(x₁, y₁), где P₂(x₂, y₂) лежит на луче необходимо и достаточно выполнения двух условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (P₁P₂, P₁M) ≥ 0 – скалярное произведение (точка лежит на луче)

Задача №3

Определить принадлежит ли точка отрезку.

Решение
Пусть точки P₁(x₁, y₁), P₂(x₂, y₂) концы заданного отрезка. Опять-таки необходимым условием принадлежности точки отрезку является ее принадлежность прямой проходящей через P₁, P₂. Далее нам нужно определить лежит ли точка между точками P₁ и P₂, для этого нам на помощь приходит скалярное произведение векторов только на этот раз других: (MP₁, MP₂). Если оно меньше либо равно нуля, то точка лежит на отрезке, иначе вне отрезка. Почему так? Посмотрим на рисунок.

Итак, для того чтобы точка M(x, y) лежала на отрезке с концами P₁(x₁, y₁), P₂(x₂, y₂) необходимо и достаточно выполнения условий:
1. [P₁P₂, P₁M] = 0 – косое произведение (точка лежит на прямой)
2. (MP₁,MP₂) ≤ 0 – скалярное произведение (точка лежит между P₁ и P₂)

Задача №4

Взаимное расположение двух точек относительно прямой.

Решение
В этой задаче необходимо определить по одну или по разные стороны относительно прямой находятся две точки.

Если точки находятся по разные стороны относительно прямой, то косые произведения имеют разные знаки, а значит их произведение отрицательно. Если же точки лежат по одну сторону относительно прямой, то знаки косых произведений совпадают, значит, их произведение положительно.
Итак:
1. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] 0 – точки лежат по одну сторону.
3. [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] = 0 – одна (или две) из точек лежит на прямой.

Кстати, задача об определении наличия точки пересечения у прямой и отрезка решается точно также. Точнее, это и есть эта же задача: отрезок и прямая пересекаются, когда концы отрезка находятся по разные стороны относительно прямой или когда концы отрезка лежат на прямой, то есть необходимо потребовать [P₁P₂, P₁M₁] * [P₁P₂, P₁M₂] ≤ 0.

Задача №5

Определить пересекаются ли две прямые.

Решение
Будем считать, что прямые не совпадают. Понятно, что прямые не пересекаются, только если они параллельны. Поэтому, найдя условие параллельности, мы можем, определить пересекаются ли прямые.
Допустим прямые заданы своими уравнениями a₁x + b₁y + c₁ = 0 и a₂x + b₂y + c₂ = 0. Тогда условие параллельности прямых заключается в том, что a₁b₂ — a₂b₁ = 0.
Если же прямые заданы точками P₁(x₁, y₁), P₂(x₂, y₂), M₁(x₃, y₃), M₂(x₄, y₄), то условие их параллельности заключается в проверки косого произведения векторов P₁P₂ и M₁M₂: если оно равно нулю, то прямые параллельны.

В общем, то когда прямые заданы своими уравнениями мы тоже проверяем косое произведение векторов (-b₁, a₁), (-b₂, a₂) которые называются направляющими векторами.

Задача №6

Определить пересекаются ли два отрезка.

Решение
Вот эта задача мне, действительно, нравится. Отрезки пересекаются тогда, когда, концы каждого отрезка лежат по разные стороны от другого отрезка. Посмотрим на рисунок:

Итак, нам нужно проверить, чтобы концы каждого из отрезков лежали по разные стороны относительного концов другого отрезка. Пользуемся косым произведением векторов. Посмотрите на первый рисунок: [P₁P₂, P₁M₂] > 0, [P₁P₂, P₁M₁] [P₁P₂, P₁M₂] * [P₁P₂, P₁M₁] 2 + b 2 ).

Задача №8

Расстояние от точки до луча.

Решение
Эта задача отличается от предыдущей тем, что в этом случае может получиться, так что перпендикуляр из точки не падает на луч, а падает на его продолжение.

В случае, когда перпендикуляр не падает на луч необходимо найти расстояние от точки до начала луча – это и будет ответом на задачу.

Как же определить падает ли перпендикуляр на луч или нет? Если перпендикуляр не падает на луч, то угол MP₁P₂ – тупой иначе острый (прямой). Поэтому по знаку скалярного произведения векторов мы можем определить попадает ли перпендикуляр на луч или нет:
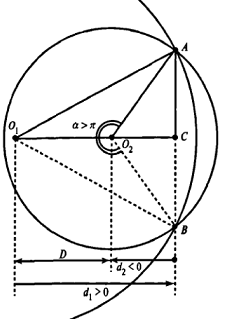
1. (P₁M, P₁P₂) 2 .

Теперь рассмотрим случай, когда центр второго круга O₂ находится между точками O₁ и C. В этом случае получим отрицательное значение величины d₂. Использование отрицательного значения d₂ приводит к отрицательному значению α. В этом случае необходимо для правильного ответа прибавить к α 2π.

Заключение

Ну вот и все. Мы рассмотрели не все, но наиболее часто встречаемые задачи вычислительной геометрии касающиеся взаимного расположения объектов.

источники:

http://espressocode.top/shortest-distance-between-a-point-and-a-circle/

http://habr.com/ru/post/148325/