Нормальное (нормированное) уравнение прямой: описание, примеры, решение задач
В данной статье рассмотрим нормальное уравнение прямой на заданной плоскости. Получим нормальное уравнение, покажем не примере, дадим определение нормирующего множителя и разберем приведение общего уравнения к нормальному виду. Заключительной части посвятим основному приложению нормального уравнения прямой, то есть нахождение расстояние от точки до прямой на плоскости.
Нормальное уравнение прямой – описание и пример
Рассмотрим выведение нормального уравнения.
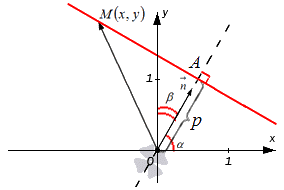
Фиксируем на плоскости систему координат О х у , где задаем прямую с точкой, через которую она проходит с нормальным вектором прямой. Нормальному вектору прямой дадим обозначение n → . Его начало обозначено точкой O . координатами являются cos α и cos β , углы которых расположены между вектором n → и положительными осями О x и O y . Это запишется так: n → = ( cos α , cos β ) . Прямая проходит через точку A с расстоянием равным p , где p ≥ 0 от начальной точки O при положительном направлении вектора n → . Если р = 0 , тогда A считается совпадающей с точкой координат. Отсюда имеем, что O A = p . Получаем уравнение, при помощи которого задается прямая.
Имеем, что точка с координатами M ( x , y ) расположена на прямой тогда и только тогда, когда числовая проекция вектора O M → по направлению вектора n → равняется p , значит при выполнении условия n p n → O M → = p .
O M → является радиус-вектором точки с координатами M ( x , y ) , значит O M → = ( x , y ) .
Применив определение скалярного произведения векторов, получим равенство вида: n → , O M → = n → · n p n → O M → = 1 · n p n → O M → = n p n → O M → = p
Тогда это же произведение будет иметь вид в координатной форме: n → , O M → = cos α · x + cos β · y
Отсюда cos α · x + cos β · y = p или cos α · x + cos β · y — p = 0 . Было выведено нормальное уравнение прямой.
Уравнение вида cos α · x + cos β · y — p = 0 называется нормальным уравнением прямой или нормированным уравнением прямой. Иначе говоря, уравнение прямой в нормальном виде.
Понятно, что такое уравнение представляет собой общее уравнение прямой A x + B y + C = 0 , где A и B имеют значения, при которых длина вектора n → = ( A , B ) равна 1 , а C является неотрицательным числом.
Теперь рассмотрим его геометрический смысл. Нормальное уравнение прямой вида cos α · x + cos β · y — p = 0 задает в системе координат О х у на плоскости прямую с наличием нормального вектора единичной длины n → = ( cos α , cos β ) , которая располагается на расстоянии равном p от начала координат по положительному направлению вектора n → .
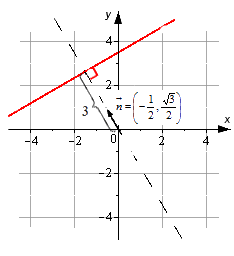
Если дано уравнение прямой вида — 1 2 · x + 3 2 · y — 3 = 0 , то на плоскости задается прямая, у которой нормальный вектор с координатами — 1 2 , 3 2 . Удаление прямой от начала координат идет по направлению, совпадающему с направлением нормального вектора n → = — 1 2 , 3 2 .
Приведение общего уравнения прямой к нормальному виду
Часто решение задач подразумевает использование нормального уравнения прямой, но само оно не дается в нормальном виде, поэтому необходимо для начала приводить к нормальному виду, после чего выполнять необходимые вычисления.
Нормальное уравнение получают из общего уравнения прямой. Когда на плоскости задается другим уравнением, то необходимо привести его к общему виду, после чего возможно приведение к нормальному. Если рассмотреть на примере, то это будет выглядеть так.
Для приведения общего уравнения прямой A x + B x + C = 0 к нормальному необходимо обе части умножить на нормирующий множитель, который имеет значение ± 1 A 2 + B 2 . Его знак определяется при помощи противоположности знака слагаемого C . При С = 0 знак выбирается произвольно.
Привести уравнение прямой 3 x — 4 y — 16 = 0 к нормальному виду.
Из общего уравнения видно, что А = 3 , В = — 4 , С = — 16 . Так как значение C отрицательное, необходимо брать положительный знак для формулы. Перейдем к вычислению нормирующего множителя:
1 A 2 + B 2 = 1 3 2 + ( — 4 ) 2 = 1 5
Теперь необходимо умножить обе части уравнения на одну пятую. Получим, что 1 5 · ( 3 x — 4 y — 16 ) = 0 ⇔ 3 5 · x — 4 5 · y — 16 5 = 0 .
Нормальное уравнение по заданной прямой найдено.
Ответ: 3 5 · x — 4 5 · y — 16 5 = 0 .
Как найти расстояние от прямой до плоскости
В этой статье дано определение расстояния между параллельными прямой и плоскостью, приведена теория, необходимая для нахождения расстояния между прямой и параллельной ей плоскостью методом координат, а также подробно разобраны решения характерных примеров и задач.
Навигация по странице.
Расстояние между параллельными прямой и плоскостью – определение.
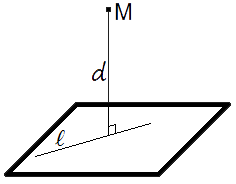
Расстояние между прямой и параллельной ей плоскостью определяется через расстояние от точки до плоскости.
Расстояние между параллельными прямой и плоскостью – это расстояние от любой точки заданной прямой до заданной плоскости.
Рассмотрим прямую a и параллельную ей плоскость 

Озвученное определение расстояния между параллельными прямой и плоскостью тесно связано со следующей теоремой.
Если прямая a параллельна плоскости 

Проведем через произвольную точку прямой a плоскость 








Нахождение расстояния между прямой и параллельной ей плоскостью – теория, примеры, решения.
Расстояние между параллельными прямой и плоскостью обычно находится с помощью методов, изученных на уроках геометрии в 10-11 классах, — с использованием теоремы Пифагора, признаков равенства или подобия треугольников, определения синуса, косинуса или тангенса угла и т.п.
Когда в трехмерном пространстве введена прямоугольная система координат и требуется вычислить расстояние между заданными параллельными прямой и плоскостью, то применяется метод координат. Сейчас мы его подробно разберем, после чего рассмотрим решения нескольких примеров.
Поставим перед собой следующую задачу.
Пусть в трехмерном пространстве зафиксирована прямоугольная система координат Oxyz , в ней заданы параллельные прямая a и плоскость 

Решение этой задачи будем строить на основе определения расстояния между прямой и параллельной ей плоскостью.
Искомое расстояние между заданными параллельными прямой и плоскостью по определению равно расстоянию от точки М1 , лежащей на прямой a , до плоскости 





Итак, алгоритм, позволяющий найти расстояние между параллельными прямой a и плоскостью 
- находим координаты
некоторой точки М1 , лежащей на заданной прямой a (это легко сделать, если знать основные виды уравнений прямой в пространстве);
- получаем нормальное уравнение заданной плоскости
вида
(для этого нужно знать основные виды уравнения плоскости и при необходимости уметь приводить уравнение плоскости к нормальному виду);
- вычисляем требуемое расстояние
между прямой a и параллельной ей плоскостью
по формуле
.
Воспользуемся полученным алгоритмом при решении задач, в которых требуется вычислить расстояние между параллельными прямой и плоскостью.
Найдите расстояние между параллельными прямой 

Очевидно, точка 

Получим нормальное уравнение плоскости 


Осталось вычислить требуемое расстояние между заданными параллельными прямой и плоскостью как расстояние от точки 

Найдите расстояние между прямой 

В рассматриваемой задаче прямая задана уравнениями двух пересекающихся плоскостей. Найдем координаты 






Теперь получим нормальное уравнение плоскости, которую задает уравнение плоскости в отрезках вида 

Осталось вычислить расстояние от точки 


Формула для вычисления расстояния от точки до плоскости
Если задано уравнение плоскости A x + B y + C z + D = 0 , то расстояние от точки M(M x , M y , M z ) до плоскости можно найти, используя следующую формулу:
| d = | |A·M x + B·M y + C·M z + D| |
| √ A 2 + B 2 + C 2 |
Примеры задач на вычисление расстояния от точки до плоскости
Решение. Подставим в формулу коэффициенты плоскости и координаты точки
d = |2·0 + 4·3 + (-4)·6 — 6| √ 4 + 16 + 16 = |0 + 12 — 24 — 6| √ 36 = |-18| 6 = 3
Ответ: расстояние от точки до плоскости равно 3.
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Определение расстояния между: 1 — точкой и плоскостью; 2 — прямой и плоскостью; 3 — плоскостями; 4 — скрещивающимися прямыми рассматривается совместно, так как алгоритм решения для всех этих задач по существу одинаков и состоит из геометрических построений, которые нужно выполнить для определения расстояния между заданными точкой А и плоскостью α. Если и есть какое-то различие, то оно состоит лишь в том, что в случаях 2 и 3 прежде чем приступить к решению задачи, следует на прямой m (случай 2) или плоскости β (случай 3) отметить произвольную точку А. При определении расстояния между скрещивающимися прямыми предварительно заключаем их в параллельные плоскости α и β с последующим определением расстояния между этими плоскостями.
Рассмотрим каждый из отмеченных случаев решения задач.
1. Определение расстояния между точкой и плоскостью.
Расстояние от точки до плоскости определяется длиной отрезка перпендикуляра, опущенного из точки на плоскость.
Поэтому решение этой задачи состоит из последовательного выполнения следующих графических операций:
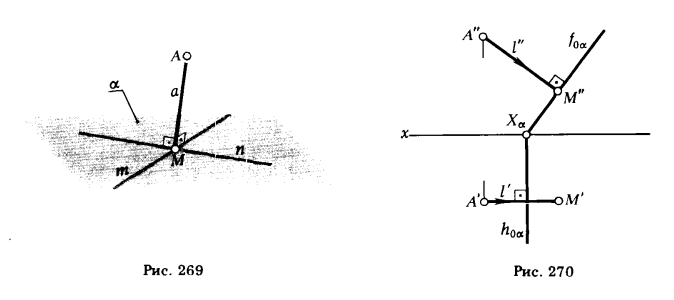
1) из точки А опускаем перпендикуляра на плоскость α (рис. 269);
2) находим точку М пересечения этого перпендикуляра с плоскостью М = а ∩ α;
3) определяем длину отрезка [AM].
Если плоскость α общего положения, то для того чтобы опустить на эту плоскость перпендикуляр, необходимо предварительно определить направление проекций горизонтали и фронтали этой плоскости. Нахождение точки встречи этого перпендикуляра с плоскостью также требует выполнения дополнительных геометрических построений.
Решение задачи упрощается, если плоскость α занимает частное положение относительно плоскостей проекций. В этом случае и проведение проекций перпендикуляра, и нахождение точки его встречи с плоскостью осуществляется без каких-либо дополнительных вспомогательных построений.
ПРИМЕР 1. Определить расстояние от точки А до фронтально проецирующей плоскости α (рис. 270).
РЕШЕНИЕ. Через А’ проводим горизонтальную проекцию перпендикуляра l’ ⊥ h0α, а через А» — его фронтальную проекцию l» ⊥ f0α. Отмечаем точку M» = l» ∩ f0α. Так как AM || π2, то [А» М»] == |АМ| = d.
Из рассмотренного примера видно, насколько просто решается задача, когда плоскость занимает проецирующее положение. Поэтому, если в исходных данных будет задана плоскость общего положения, то, прежде чем приступить к решению, следует перевести плоскость в положение, перпендикулярное к какой-либо плоскости проекции.
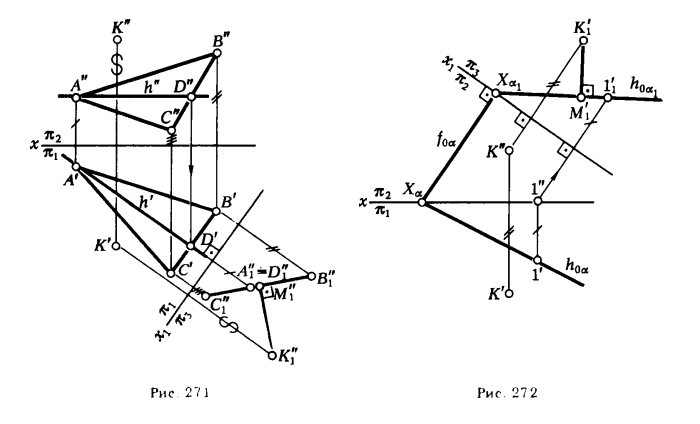
ПРИМЕР 2. Определить расстояние от точки К до плоскости, заданной ΔАВС (рис. 271).
1. Переводим плоскость ΔАВС в проецирующее положение *. Для этого переходим от системы xπ2/π1 к x1π3/π1: направление новой оси х1 выбирается перпендикулярным к горизонтальной проекции горизонтали плоскости треугольника.
2. Проецируем ΔАВС на новую плоскость π3 (плоскость ΔАВС спроецируется на π3, в [ С»1В»1] ).
3. Проецируем на ту же плоскость точку К (К’ → К»1).
Решение задачи упрощается, если плоскость задана следами, так как отпадает необходимость в проведении проекций линий уровня.
ПРИМЕР 3. Определить расстояние от точки К до плоскости α, заданной следами (рис. 272) .
* Наиболее рациональным путем перевода плоскости треугольника в проецирующее положение является способ замены плоскостей проекций, так как в этом случае достаточно построить только одну вспомогательную проекцию.
РЕШЕНИЕ. Заменяем плоскость π1 плоскостью π3, для этого проводим новую ось x1 ⊥ f0α. На h0α отмечаем произвольную точку 1′ и определяем ее новую горизонтальную проекцию на плоскости π3 (1′1). Через точки Xα1 (Хα1 = h0α1 ∩ x1 ) и 1′1 проводим h0α1. Определяем новую горизонтальную проекцию точки К → К’1. Из точки К’1 опускаем перпендикуляр на h0α1 и отмечаем точку его пересечения с h0α1 — М’1. Длина отрезка K’1M’1 укажет искомое расстояние.
2. Определение расстояния между прямой и плоскостью.
Расстояние между прямой и плоскостью определяется длиной отрезка перпендикуляра, опущенного из произвольной точки прямой на плоскость (см. рис. 248).
Поэтому решение задачи по определению расстояния между прямой m и плоскостью α ничем не отличается от рассмотренных в п. 1 примеров на определение расстояния между точкой и плоскостью (см. рис. 270 . 272). В качестве точки можно брать любую точку, принадлежащую прямой m.
3.Определение расстояния между плоскостями.
Расстояние между плоскостями определяется величиной отрезка перпендикуляра, опущенного из точки, взятой на одной плоскости, на другую плоскость.
Из этого определения вытекает, что алгоритм решения задачи по нахождению расстояния между плоскостями α и β отличается от аналогичного алгоритма решения задачи по определению расстояния между прямой m и плоскостью α лишь тем, что прямая m должна принадлежать плоскости α, т. е., чтобы определить расстояние между плоскостями α и β, следует:
1) взять в плоскости α прямую m;
2) выделить на прямой m произвольную точку А;
3) из точки А опустить перпендикуляр l на плоскость β;
4) определить точку М — точку встречи перпендикуляра l с плоскостью β;
5) определить величину отрезка [AM] .
На практике целесообразно пользоваться другим алгоритмом решения, который будет отличаться от приведенного лишь тем, что, прежде чем приступить к выполнению первого пункта, следует перевести плоскости в проецирующее положение.
Включение в алгоритм этой дополнительной операции упрощает выполнение всех без исключения остальных пунктов, что, в конечном счете, приводит к более простому решению.
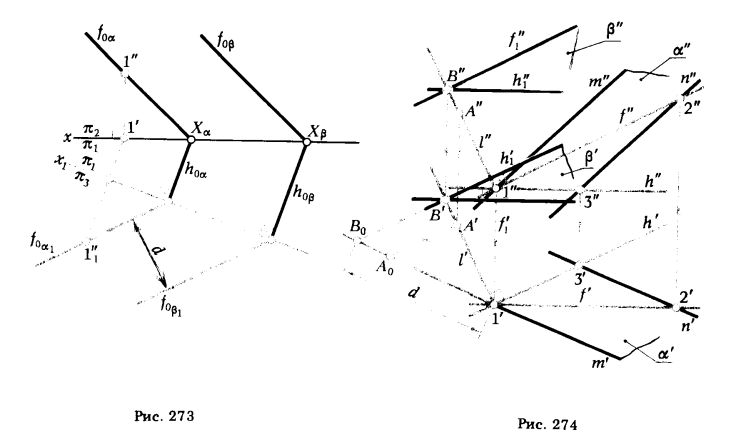
ПРИМЕР 1. Определить расстояние между плоскостями α и β (рис. 273).
РЕШЕНИЕ. Переходим от системы xπ2/π1 к x1π1/π3. По отношению к новой плоскости π3 плоскости α и β занимают проецирующее положение, поэтому расстояние между новыми фронтальными ,следами f0α1 и f0β1 является искомым.
В инженерной практике часто приходится решать задачу на построение плоскости, параллельной данной и удаленной от нее на заданное расстояние. Приведенный ниже пример 2 иллюстрирует решение такой задачи.
ПРИМЕР 2. Требуется построить проекции плоскости β, параллельной данной плоскости α (m || n), если известно, что расстояние между ними равно d (рис. 274).
1. В плоскости α проводим произвольные горизонталь h (1, 3) и фронталь f (1,2).
2. Из точки 1 восставляем перпендикуляр l к плоскости α(l’ ⊥ h’, l» ⊥ f»).
3. На перпендикуляре l отмечаем произвольную точку А.
4. Определяем длину отрезка [1А] — [1’А0] (положение [1’А0] указывает на эпюре метрически неискаженное направление прямой l).
5. Откладываем на прямой (1’А0) от точки 1′ отрезок [1’В0] = d.
6. Отмечаем на проекциях l’ и l» точки В’ и В», соответствующие точке В0.
7. Через точку В проводим плоскость β (h1 ∩ f1). Чтобы β || α, необходимо coблюдать условие h1 || h и f1 || f.
4. Определение расстояния между скрещивающимися прямыми.
Расстояние между скрещивающимися прямыми определяется длиной перпендикуляра, заключенного между параллельными плоскостями, которым принадлежат скрещивающиеся прямые.
Для того чтобы через скрещивающиеся прямые m и f провести взаимно параллельные плоскости α и β, достаточно через точку А (А ∈ m) провести прямую р, параллельную прямой f, а через точку В (В ∈ f) — прямую k, параллельную прямой m. Пересекающиеся прямые m и р, f и k определяют взаимно параллельные плоскости α и β (см. рис. 248, е). Расстояние между плоскостями α и β равно искомому расстоянию между скрещивающимися прямыми m и f.
Можно предложить и другой путь для определения расстояния между скрещивающимися прямыми, который состоит в том, что с помощью какого-либо способа преобразования ортогональных проекций одна из скрещивающихся прямых переводится в проецирующее положение. В этом случае одна проекция прямой вырождается в точку. Расстояние между новыми проекциями скрещивающихся прямых (точкой A’2 и отрезком C’2D’2) является искомым.
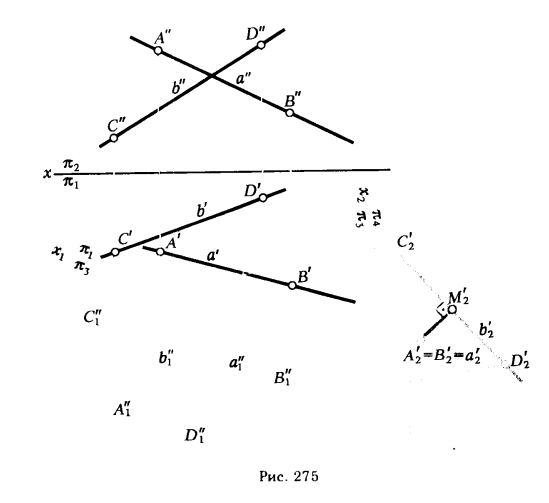
На рис. 275 приведено решение задачи на определение расстояния между скрещивающимися прямыми а и b, заданными отрезками [АВ] и [ CD]. Решение выполняют в следующей последовательности:
1. Переводят одну из скрещивающихся прямых (а) в положение, параллельное плоскости π3; для этого переходят от системы плоскостей проекции xπ2/π1 к новой x1π1/π3 , ось x1 проводят параллельно горизонтальной проекции прямой а . Определяют а»1 [А»1В»1] и b»1 [C»1D»1].
2. Путем замены плоскости π1 плоскостью π4 переводят прямую
а в положение а’2, перпендикулярное плоскости π4 (новую ось х2 проводят перпендикулярно а»1).
3. Строят новую горизонтальную проекцию прямой b’2 — [ C’2D’2].
4. Расстояние от точки А’2 до прямой C’2D’2 ( отрезок ( А’2М’2] (является искомым.
Следует иметь в виду, что перевод одной из скрещивающихся прямых в проецирующее положение является ничем иным, как переводом плоскостей параллелизма, в которые можно заключить прямые а и b, также в проецирующее положение.
В самом деле, переведя прямую а в положение, перпендикулярное плоскости π4, мы обеспечиваем перпендикулярность любой плоскости, содержащей прямую а, плоскости π4, в том числе и плоскости α, определяемой прямыми а и m (а ∩ m, m || b). Если мы теперь проведем прямую n, параллельную а и пересекающую прямую b, то мы получим плоскость β, являющуюся второй плоскостью параллелизма, в которую заключены скрещивающиеся прямые а и b. Так как β || α, то и β ⊥ π4.
Расстояние от точки до плоскости онлайн
С помощю этого онлайн калькулятора можно найти расстояние от точки до заданной плоскости. Дается подробное решение с пояснениями. Для вычисления расстояния от точки до плоскости введите координаты точки и коэффициенты уравнения плоскости в ячейки и нажимайте на кнопку «Решить».
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Расстояние от точки до плоскости − теория, примеры и решения
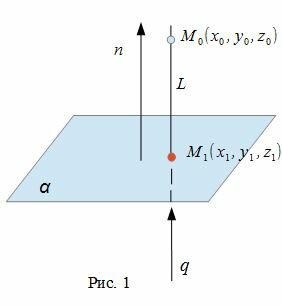
Для нахождения расстояния от точки M0 до плоскости α, необходимо найти расстояние от точки M0 до проекции точки M0 на плоскость α:
Нахождение расстояния от точки до плоскости содержит следующие шаги:
- построение прямой L, проходящей через точку M0 и перпендикулярной плоскости α.
- нахождение точки M1 пересечения плоскости α с прямой L(Рис.1).
- вычисление расстояния между точками M0 и M1.
 |
1. Общее уравнение плоскости имеет вид:
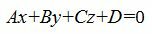 | (1) |
где n(A,B,C)− называется нормальным вектором плоскости.
Уравнение прямой, проходящей через точку M0(x0, y0, z0) и имеющий направляющий вектор q(l, m, n) имеет следующий вид:
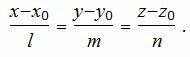 | (2) |
Для того, чтобы прямая (2) была ортогональна плоскости (1), направляющий вектор q(l, m, n) прямой (2) должен быть коллинеарным нормальному вектору n(A,B,C) плоскости (1)(Рис. 1). Следовательно, в качестве направляющего вектора прямой (2) можно взять нормальный вектор плоскости (1) .
Таким образом, уравнение прямой, проходящей через точку M0(x0, y0, z0) и ортогональной плоскости (1) имеет следующий вид:
 | (3) |
Для нахождения точку пересечения прямой L с плоскостью α, проще всего рассматривать параметрическое уравнение прямой. Составим ее
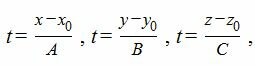 |
Выразим переменные x, y, z через рараметр t.
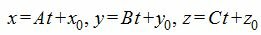 | (4) |
2. Найдем точку пересечения прямой (4) с плоскостью (1). Для этого нужно найти такой параметр t, при котором точка M(x, y, z) принадлежит плоскости (1). Поэтому подставим значения x,y,z из выражения (4) в (1) и решим относительно t.
| A(At+x0)+B(Bt+y0)+C(At+z0)+D=0, |
| A 2 t+Ax0+B 2 t+By0+C 2 t+Cz0+D=0, |
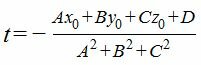 | (5) |
3. Найдем, наконец, расстояние от точки M0 до плоскости (1). Очевидно, что расстояние от точки M0 до плоскости (1) − это расстояние от точки M0 до точки M1. А это расстояние вычисляется так:
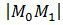 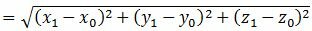 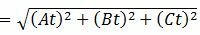 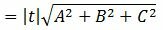 |
Учитывая значение параметра t, имеем:
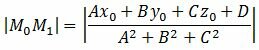  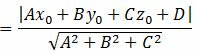 | (6) |
Пример 1. Найти расстояние от точки M0(2, -1, -9/31) до плоскости
 | (7) |
Нормальный вектор плоскости имеет вид:
Подставляя координаты точки M0 и нормального вектора плоскости в (5), получим:
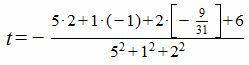 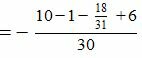  | (8) |
Из выражений (4) находим:
 |
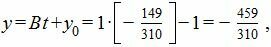 |
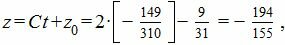 |
Проекцией точки M0(2, -1, -9/31) на плоскость (7) является точка:
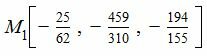 . . |
Вычислим расстояние между точками M0 и M1:
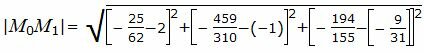 . . |
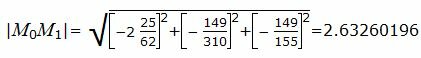 . . |
Расстояние от точки M0(2, -1, -9/31) до плоскости (7):
http://hd01.ru/info/kak-najti-rasstojanie-ot-prjamoj-do-ploskosti/
http://matworld.ru/analytic-geometry/rasstojanie-tochka-ploskost-online.php