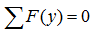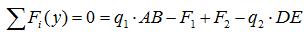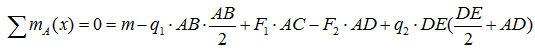Уравнение равновесия балки в перемещениях

iSopromat.ru

Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.

Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.

При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.

В результате имеем следующие уравнения статики:

1. Сумма проекций всех сил на вертикальную ось равна нулю
   
2. Сумма моментов относительно любой точки системы тоже равна нулю.
   

Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.

Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A :

Дополнительные материалы

• Порядок определения момента от распределенной нагрузки.
• Правила знаков при составлении уравнений статики для систем находящихся в равновесии.

Совместное решение системы полученных уравнений позволяет определить величину и направление двух неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Решение задач, контрольных и РГР

Стоимость мы сообщим в течение 5 минут
на указанный вами адрес электронной почты.

Если стоимость устроит вы сможете оформить заказ.

НАБОР СТУДЕНТА ДЛЯ УЧЁБЫ

— Рамки A4 для учебных работ
— Миллиметровки разного цвета
— Шрифты чертежные ГОСТ
— Листы в клетку и в линейку

Определение реакций опор балки – решение задачи

Как определить реакции опор балки

Пример решения задачи на определение реакций опор балки

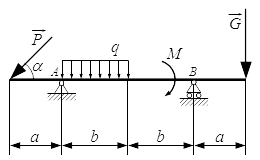
Жесткая балка, линейные размеры которой указаны на рисунке 1, закреплена в точках А и В. На балку действуют пара сил с моментом М, равномерно распределенная нагрузка интенсивностью q и две силы P и G, место приложения которых показано на рисунке.
Определить реакции опор балки в точках A и B, вызываемые указанными нагрузками.

Дано:
P = 20,2 Н ; G = 22,6 Н ; q = 2 Н/м ; M = 42,8 Н·м ; a = 1,3 м ; b = 3,9 м ; α = 45° ;

Решение задачи

Проводим оси x и y системы координат. Начало системы координат поместим в точку A . Ось x направим горизонтально, вдоль балки. Ось y – вертикально. Ось z перпендикулярна плоскости рисунка и направлена на нас. На рисунке она не указана.

Силы, действующие на балку.

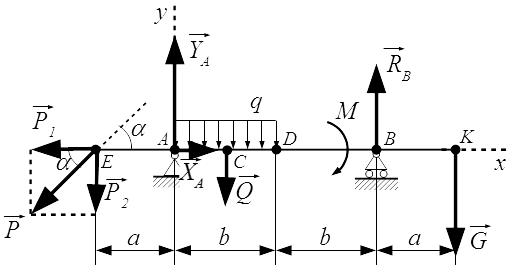
Отбрасываем опоры и заменяем их силами реакций.
В шарнире A , разложим силу реакции на составляющие и вдоль осей координат.
Реакция , в подвижной опоре на катках, направлена вертикально. Предполагаемые направления реакций опор выбираем по своему усмотрению, наугад. Если ошибемся с направлением реакции, то получим отрицательное значение, что будет говорить о том, что соответствующая сила реакции направлена в противоположную сторону.

Заменим равномерно распределенную нагрузку q равнодействующей . Абсолютное значение равнодействующей равно площади эпюры:
Н .
Точка приложения равнодействующей находится в центре тяжести эпюры. Поскольку эпюра представляет собой прямоугольник, то ее центр тяжести находится в точке C – посередине отрезка AD :
AC = CD = b/2 = 1,95 м .

Уравнения равновесия для сил

Определяем проекции сил на оси координат.

Разложим силу на составляющие вдоль координатных осей:
.
Абсолютные значения составляющих:
.
Вектор параллелен оси x и направлен в противоположную от нее сторону. Вектор параллелен оси y и также направлен в противоположную сторону. Поэтому проекции силы на оси координат имеют следующие значения:
.

Остальные силы параллельны осям координат. Поэтому они имеют следующие проекции:
;
;
;
;
.

Составляем уравнения равновесия для сил.
Сумма проекций всех сил на ось x равна нулю:
;
;
;
(П1) .

Сумма проекций всех сил на ось y равна нулю:
;
;
;
(П2) .

Уравнения равновесия для моментов

Итак, мы уже составили два уравнения для сил: (П1) и (П2). Но в них есть три неизвестные величины: , и . Чтобы их определить, нам нужно составить еще одно уравнение.

Составим уравнение равновесия для моментов сил. Для этого нам нужно выбрать ось, относительно которой мы будем вычислять моменты. В качестве такой оси возьмем ось, проходящую через точку A , перпендикулярно плоскости рисунка. За положительное направление выберем то, которое направлено на нас. Тогда, по правилу правого винта, положительным направлением закручивания будет направление против часовой стрелки.

Находим моменты сил относительно выбранной оси.
Силы , и пересекают ось. Поэтому их моменты равны нулю:
; ; .

Сила перпендикулярна плечу AB . Ее момент:
.
Поскольку, относительно оси A , сила направлена против часовой стрелки, то ее момент положительный.

Сила перпендикулярна плечу AK . Поскольку, относительно оси A , эта сила направлена по часовой стрелки, то ее момент имеет отрицательное значение:
.

Аналогичным способом находим моменты остальных сил:
;
.
Момент от пары сил M не зависит от точек приложения сил, входящих в пару:
.

Составляем уравнение равновесия. Сумма моментов сил относительно оси A равна нулю:
;

;
;
(П3) .

Решение уравнений равновесия

Итак, для трех неизвестных величин, мы получили три уравнения:
(П1) .
(П2) .
(П3) .

Решаем эти уравнения. Вычисляем расстояния.
м;
м;
м;
м.

Из уравнения (П1) находим:
Н.
Из уравнения (П3) находим:

Н.
Из уравнения (П2) имеем:
Н.
Абсолютное значение реакции опоры в точке A :
Н.

Проверка правильности решения

Чтобы проверить, правильно ли мы определили реакции опор балки, найдем сумму моментов сил относительно другой оси. Если мы нашли реакции правильно, то она должна равняться нулю.

Возьмем ось, проходящую через точку E . Вычисляем сумму моментов сил относительно этой оси:

.
Найдем погрешность вычисления суммы моментов. Найденные силы мы округлили до двух знаков после запятой. То есть погрешность определения реакций опор составляет 0,01 Н . Расстояния, по порядку величины, примерно равны 10 м. Тогда погрешность вычисления суммы моментов составляет около 10·0,01 = 0,1 Нм . Мы получили значение -0,03 Нм . Эта величина отличается от нуля не более, чем на величину погрешности. То есть, с учетом погрешности вычислений, сумма моментов относительно другой оси равна нулю. Значит решение правильное, силы реакций найдены верно.

Второй способ решения

Первым способом мы составили два уравнения для сил и одно – для моментов. Задачу можно решить другим способом, составив два уравнения для моментов и одно для сил.

Воспользуемся тем, что сумма моментов сил равна нулю относительно любой оси. Возьмем вторую ось, которая проходит через точку B перпендикулярно плоскости рисунка. Сумма моментов сил относительно этой равна нулю:
.
Вычисляем моменты сил относительно оси B .
; ; ;
;
;
;
;
.

Сумма моментов сил относительно оси B равна нулю:
;

;
;
(П4) ;

Итак, вторым способом, мы также имеем три уравнения:
(П1) .
(П3) ;
(П4) .

Здесь каждое уравнение содержит только одну неизвестную величину. Реакции и определяются из тех же уравнений, что и ранее. Находим силу из уравнения (П4):

Н.

Значение реакции совпало со значением, полученным первым способом из уравнения (П2).

Автор: Олег Одинцов . Опубликовано: 14-10-2017 Изменено: 28-12-2021

Расчёт статически определимой балки

Расчёт статически определимой

Методическое пособие для выполнения расчётно-графической работы

«Расчёт статически определимой консольной балки на прочность и жёсткость»

Методическое пособие предназначено для студентов инженерных специальностей и используется при выполнении расчётно-графической работы «Расчёт статически определимой балки на прочность и жёсткость». Здесь в приводятся необходимые теоретические сведения по существу выполняемой работы. Представлен численный пример – образец выполнения этой работы, сопровождаемый соответствующими комментариями. Методическое пособие завершаются заданием, исходными данными для выполнения расчётно-графической работы и требованиями к её оформлению.

Лауреат Государственной премии СССР,

1. Краткая характеристика работы

Расчётно-графическая работа (РГР) состоит из двух частей. В первой части осуществляется расчёт на прочность статически определимой консольной балки, находящейся под действием поперечной нагрузки. Здесь строятся эпюры поперечных сил и изгибающих моментов, осуществляется подбор поперечного сечения балки оптимальной формы из условия прочности по нормальным напряжениям, осуществляется полная проверка прочности балки. Во второй части работы оценивается жёсткость запроектированной балки в пролёте и на консоли. Здесь вычисляются прогибы балки в указанных в задании точках, строится упругая линии и определяются максимальные прогибы в пролёте балки и на её консоли.

2. Сведения из теории

Прежде чем приступить к выполнению расчётно-графической работы необходимо вспомнить некоторые сведения из курса сопротивления материалов, относящиеся к основам теории изгиба балок

2.1 Объектом, рассматриваемым в настоящей работе, является балка, именно, консольная балка, то есть однопролётная балка, имеющая консоль.

Балкой называют прямой брус, имеющий опорные закрепления и работающий на изгиб под действием поперечной нагрузки. Плоским прямым изгибом балки определяется случай, когда балка имеет вертикальную плоскость симметрии, в этой плоскости действуют приложенные нагрузки и в этой же плоскости происходит изгиб оси балки. В РГР рассматривается именно этот случай.

Пролётом балки называется расстояние между её опорами.

2.2. Расчётной схемой балки определяется ось балки, как геометрическое место точек – центров тяжести поперечных сечений физической балки. К оси балки прикладываются нагрузки, ось балки опирается на опоры, создавая, таким образом, геометрически неизменяемую систему. Изогнутая, деформированная, ось балки называется упругой линией балки, а расстояние по вертикали между точками на деформированной и не деформированной осях балки называется прогибом балки

Далее считаем, что начало координат совпадает с левой опорой балки; ось Х совпадает с осью стержня и направлена в право; ось У, перпендикулярна оси 0Х, направлена в верх и размещается в плоскости чертежа; ось Z размещается в поперечном сечении балки и перпендикулярна плоскости чертежа.

2.3. Нагрузки, приложенные к балке, подразделяются на три вида:

— сосредоточенная сила величиной Р, кН;

— равномерно распределённая нагрузка интенсивности q, кН/м;

— сосредоточенный момент величиной М, кН·м.

2.4. Балка, рассматриваемая в РГР, имеет шарнирные опорные закрепления, именно шарнирную неподвижную опору и шарнирно подвижную опору. Шарнирно неподвижная опора исключает все линейные перемещения, допуская только угловое перемещение (поворот) сечения; шарнирно подвижная опора допускает как линейное, так и угловое перемещение.

В шарнирно неподвижной опоре возникает опорная реакция в виде сосредоточенной силы, проходящей через опорный шарнир. Эта реакция обычно представляется в виде двух компонент – горизонтальной и вертикальной составляющих.

В шарнирно подвижной опоре возникает опорная реакция, направленная по опорному стержню.

Если действуют вертикальные нагрузки и стержень шарнирно подвижной опоры направлен вертикально, то опорные реакции в шарнирных опорах тоже будут направлены вертикально. В балке из РГР таких опорных реакция будет всего две.

Кроме упомянутых выше шарнирных опор, существуют и другие виды опорных закреплений, в частности жёсткое защемление (консоль – балка с жёстким защемлением одного из её торцов).

2.5.. Для плоской системы параллельных сил существует только два линейно независимых уравнений равновесия. Удобно составлять эти уравнения в виде равенства нулю суммы моментов всех сил относительно каждой из опор. В этом случае в каждом из уравнений будет фигурировать только одна из неизвестных реакций.

Уравнение равновесия балки в форме суммы проекций сил на ось 0У используется обычно для формальной проверки правильности найденных значений опорных реакций.

2.6. К внешним силам относят нагрузки, приложенные к балке (п. 2.3) и опорные реакции.

2.7. Гипотеза плоских сечений. Считается, что при изгибе балок справедлива гипотеза плоских сечений. Именно, любое поперечное сечение балки не деформируется, остаётся жёстким и при изгибе лишь поворачиваются относительно некоторой нейтральной оси z-z, проходящей в плоскости поперечного сечения.

2.8. При изгибе балки в её поперечных сечениях возникают внутренние силы: изгибающие моменты – МZ , кН·м и поперечные силы – QУ, кН Обычно индексы при М и Q, определяющие их действие, опускают, так как при плоском поперечном изгибе других внутренних сил не существует.

Поперечная сила в сечении балки имеет положительное направление, если равные между собой правая и левая поперечные силы в сечении образуют пару сил с вращением против часовой стрелки.

Изгибающим моментам в сечении знак не присваивается, однако направление их действия связывается со сжатыми (растянутыми) волокнами в крайних фибрах сечения.

2.9. Эпюрой называется график изменения некоторой характеристики Z. Для балок обычно строят эпюры поперечных сил Q и эпюры изгибающих моментов М.

Построение эпюр связано с методом сечений, применяемым для выявления внутренних сил и выяснения характера изменения этих сил. Балка рассекается сечением на две части, одна из которых отбрасывается, а её действие на оставшуюся часть заменяется силами (внутренними), — поперечной силой Q и изгибающим моментом М.

В балке определяются, так называемые, грузовые участки. Это участки с непрерывным изменением нагрузки (функция нагрузки дифференцируема), влияющей на вид функций Q(х), или М(х).

2.9.1. Для построения эпюры поперечных сил необходимо выявить функциональную зависимость Q(х) на данном грузовом участке. Для этого проводят сечение на этом участке, отбрасывают какую-либо часть балки (обычно с преобладающей нагрузкой) и вводят положительно направленную поперечную силу (для левой части балки, направленной вниз, а для правой – вверх). Составляется уравнение равновесия рассматриваемой части балки в виде равенства нулю проекций всех сил, включая силу Q(x), на вертикальную ось 0У. Отсюда находят функциональное выражение поперечной силы Q(x) и приступают к изображению изменения этой силы на грузовом участке, придавая абсциссе х фиксированные значения. В РГР эпюра силы Q(x) может быть изображена в двух вариантах: это либо линейная функция в случае участка с распределённой нагрузкой, либо константа во всех остальных случаях.

Если значение поперечной силы, полученное из уравнения равновесия, имеет отрицательный знак, то исходное направление поперечной силы должно быть изменено на противоположно.

В точке приложения сосредоточенной силы Р на эпюре поперечных сил имеет место скачёк, равный величине этой силы.

2.9.2. Для построения эпюры изгибающих моментов необходимо выявить функциональную зависимость М(х) на данном грузовом участке. Производят сечение на этом участке, отбрасывают какую-либо часть балки (обычно с преобладающей нагрузкой) и вводят в сечении сосредоточенный момент, направленный таким образом, чтобы сжатыми оказались верхние волокна сечения. Для исключения ошибки в выборе направления изгибающего момента в сечении можно использовать «правило пальца», когда сжатая и растянутая кожа пальца определяется направлением приложенного к пальцу момента.

Уравнение равновесия отсечённой части составляется в виде равенства нулю суммы моментов всех приложенных сил относительно сечения оси балки. Отсюда находят функциональное выражение изгибающего момента М(x) и приступают к его изображению на соответствующем грузовом участке, придавая абсциссе х фиксированные значения. В РГР эпюра М(х) может быть изображена в двух вариантах: это либо квадратная парабола в случае участка с распределённой нагрузкой, либо линейная функция, включая константу, во всех остальных случаях.

Если эпюра изгибающих моментов размещается на сжатых волокнах балки, то справедливо привило «антипаруса», то есть действие распределённой нагрузки и выпуклость эпюры моментов (паруса) направлены в противоположные стороны.

В точке приложения сосредоточенной силы Р на эпюре моментов изменяется направление, то есть в этой точке у функции (графика) изгибающих моментов одновременно существую две производных – правая и левая

В точке приложения сосредоточенного момента М на эпюре изгибающих моментов имеет место скачок, численно равный величине этого момента.

2.9.3. Дифференциальные зависимости при изгибе выводятся из условий равновесия элемента балки длинной dx.

При принятой системе координат (п. 2.2), положительном (вверх) направлении нагрузки q(x) и сжатых верхних волокон балки получим следующие дифференциальные зависимости:

,(2.1)

, (2.2)

или, объединяя оба эти выражения:

. (2.3)

Интегрирование дифференциальных выражений приводит к следующим интегральным выражениям:

, (2.4)

, (2.5)

или, объединяя, получим:

. (2.5)

Здесь С1 и С2 – постоянные интегрирования.

В РГР на грузовых участках действует распределённая нагрузка постоянной интенсивности q(x) = const = q, в том числе и q = 0, поэтому из уравнений (2.1) – (2.5) следует:

, (2.6)

, (2.7)

то есть поперечная сила суть постоянная величина, а изгибающий момент – линейная функция;

, (2.8)

, (2.9)

то есть поперечная сила суть линейная функция, а изгибающий момент – квадратная парабола.

Из формулы (2.2) следует, что если эпюра поперечных сил пересекает ось эпюры (Q(x) = 0 в точке пересечения), то значение изгибающего момента в этой же точке будет иметь экстремальное значение (необходимое условие экстремума).

2.10. Под действием внешней нагрузки в балке возникают напряжения – внутренние силы, действующие по элементарным площадкам. При изгибе, в поперечном сечении, возникает два вида напряжений: нормальные σ и касательные τ. Нормальные напряжения действуют по нормали к площадке, а касательные – в плоскости площадки. Нормальные и касательные напряжения измеряются в Паскалях (Па), 1 Па = 1 H/м2.

Для балки симметричного сечения при плоском изгибе и нормальные и касательные, напряжения меняются по высоте сечения и остаются одинаковыми в точках сечения при постоянной ординате.

2.10.1. Нормальные напряжения в сечении балки при изгибе определяются выражением:

, (2.10)

Здесь М(х) – изгибающий момент в сечении с абсциссой х; у – ордината точки поперечного сечения, в которой определяется σ; IZ, м4 – осевой момент инерции поперечного сечения балки относительно оси z — z

Если поперечное сечение балки высотой h имеет две оси симметрии — вертикальную y и горизонтальную z (именно этот случай рассматривается в РГР), то максимальное и минимальное нормальные напряжения возникают в крайних фибрах поперечного сечения (при y =± h/2) и будут одинаковыми по модулю. То есть

, (2.11)

здесь , м3 – осевой момент сопротивления поперечного сечения балки.

2.10.2. Касательные напряжения в точке поперечного сечения балки при изгибе определяются формулой Журавского:

, (2.12)

где Q(x) — значение поперечной силы в сечении балки с абсциссой х; , м3 — статический момент отсечённой части поперечного сечения с ординатой y относительно оси z—z; — ширина поперечного сечения балки при ординате у; — осевой момент инерции поперечного сечения балки относительно оси z—z.

Максимальная величина касательного напряжения определяется наибольшим значением статического момента и наименьшим значением ширины поперечного сечения .

2.11. Сечение балки подбирается из условия прочности по нормальным напряжениям. Именно, максимальные значения нормальных напряжений, возникающих в балке (максимальный изгибающий момент определяется по эпюре моментов), не должны превышать допускаемых нормальных напряжений [σ]:

, (2.13)

отсюда определяется наименьшее (из возможных) значение момента сопротивления:

, (2.14)

по величине которого и подбирается требуемое поперечное сечение, например, из двутавра по сортаменту прокатных профилей (см. Приложение, таблица 1). Прокатный двутавр является наиболее оптимальным балочным профилем, так как большая часть материала двутавра сосредоточена в его полках, где как раз и возникают наибольшие нормальные напряжения.

2.12. Если задано поперечное сечение балки, построена эпюра изгибающих моментов и определено максимальное значение – Мmax, то проверка прочности по нормальным напряжениям проводится согласно формулы (2.13).

Полная проверка прочности, кроме проверки по нормальным напряжениям, включает проверку прочности по касательным напряжениям и проверку прочности при совместном действии нормальных и касательных напряжений в точке.

Для проверки прочности по касательным напряжениям по эпюре поперечных сил определяется максимальное значение Qmax (обычно на опоре балки) и по формуле Журавского при заданном допускаемом напряжении [τ]осуществляется эта проверка:

. (2.15)

Случай проверки прочности при совместном действии нормальных и касательных напряжений реализуется таким образом. По эпюрам изгибающих моментов и поперечных сил определяются такие сечения (одно, два или три), где изгибающий момент и поперечная сила одновременно достигают достаточно больших значений. Далее в поперечном сечении балки определяют точку, где также одновременно велики нормальные и касательные напряжения (для двутавра эта точка находится в месте сопряжения полки и стенки) и находят эти напряжения по формулам (2.10) и (2.12) . Наконец, выбирается рекомендуемая гипотеза прочности и осуществляется эта проверка. Для изделий из малоуглеродистой стали (балочные профили), это – третья гипотеза прочности (наибольших касательных напряжений):

(2.16)

или четвёртая гипотеза прочности (энергетическая – наибольшей энергии деформации формоизменения):

(2.17)

2.13. Дифференциальное уравнение поперечного изгиба статически определимой балки постоянной жёсткости имеет вид:

, (2.18)

здесь , Н·м2 — жёсткость сечения балки при изгибе, , Па — модуль упругости, — осевой момент инерции, у(х) – прогиб балки, М(х) — изгибающий момент.

Знак (+) или (-) в уравнении (2.18) ставится в соответствии со знаком кривизны балки в точке, то есть в зависимости от принятого знака изгибающего момента и направления оси у. Если считать положительным направление изгибающих моментов при сжатии верхних волокон, а ось у направить вверх, то знак в уравнении (2.18) будет положительным.

Последовательное интегрирование уравнения (2.18) приводит к выражениям функции углов поворота (2.19) и функции прогиба (2.20), определённых на участке с постоянной жёсткостью и при дважды дифференцируемой функциии изгибающего момента М(х):

, (2.19)

, (2.20)

где D1 и D2 – постоянные интегрирования, определяемые из кинематических (по линейному и угловому перемещениям) граничных условий.

Проинтегрированное выражение (2.20) с найденными граничными условиями носит название упругой линии балки.

Граничные условия балки определяются её закреплениями. В месте жёсткого закрепления балки, в случае жёсткой заделки, равны нулю её прогиб и угол поворота её сечения. В случае шарнирного опирания как это имеет место в РГР, равны нулю прогибы балки на каждой из ей опор. При стыковании двух грузовых участков балки, в качестве граничных формируются условия гладкости упругой линии в месте стыка. Именно, составляются уравнения равенства прогибов и углов поворота на стыке обеих частей.

2.14. При определённых условиях уравнение упругой линии может быть представлено для любого участка балки в следующей формализованной стандартной форме:

, (2.21)

в таком виде уравнение (2.21) носит название – универсального уравнения упругой линии балки. Здесь и прогиб и угол поворота сечения балки в начале координат (в РГР это левая опора), эти начальные параметры определяются из условий закрепления балки; М, Р и q – элементы нагрузки балки, соответственно, сосредоточенные момент и сила, а также интенсивность равномерно распределённой нагрузки; символом с для к-ой нагрузки обозначена разность ск = х – ак, где ак обозначено расстояние от к-ой нагрузки до начала координат, а х – абсцисса сечения. Подчеркнём, что действующая распределённая нагрузка q не обрывается, а для учёта её фактической конечности к балке прикладывается компенсирующая нагрузка противоположного направления

Дифференцируя выражение (2.21) один раз получим универсальное уравнение углов поворота (2.22) в аналогичной форме:

. (2.22)

Для построения линии прогибов в РГР достаточно использовать только уравнение (2.21).

2.15. Проверка жёсткости балки осуществляется сравнением относительной величины максимального прогиба балки с некоторым нормативным значением, принимаемым в зависимости от назначения балки. Относительный прогиб балки определяется отношением величины максимального прогиба fmax к длине пролёта балки (длине консоли) l. Нормативное значение относительного прогиба балки [f/l] меняется в пределах примерно от 1/100 до 1/500. Условие жёсткости балки принимает вид:

. (2.23)

3. Пример выполнения РГР

Министерство сельского хозяйства Российской Федерации

Федеральное государственное образовательное учреждение

Ставропольский государственный аграрный университет