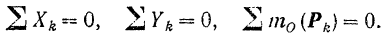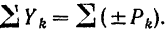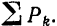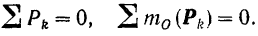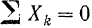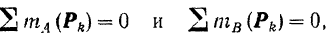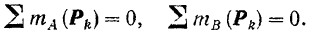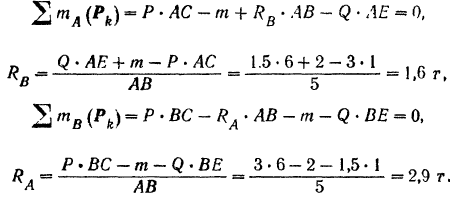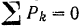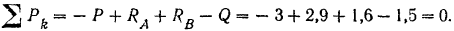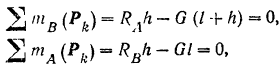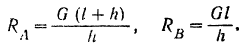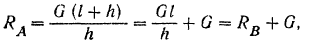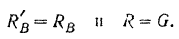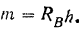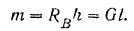Уравнения равновесия плоской системы параллельных сил
Уравнения равновесия плоской системы параллельных сил
Так как параллельное расположение сил на плоскости является частным случаем их произвольного на ней расположения, то к такой системе также могут быть применены установленные в предыдущем параграфе три уравнения равновесия плоской системы сил:
Пользуясь тем, что оси проекций можно располагать в плоскости действия сил как угодно, проведем ось 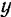
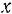
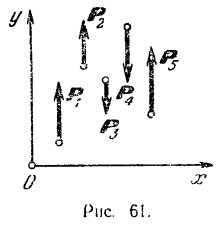
Проекция каждой из сил на ось 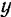
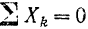
Так как все данные силы параллельны оси 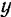
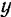
Для простоты будем в дальнейшем обозначать эту сумму просто
Таким образом, уравнения равновесия для плоской системы параллельных сил принимают вид
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю алгебраическая сумма всех сил и сумма алгебраических величин моментов всех сил относительно любой точки, лежащей в плоскости действия сил.
Вспоминая сказанное на стр. 83 о третьей возможной форме уравнении равновесия плоской системы сил (уравнения (28)), уравнениям равновесия плоской системы параллельных сил можно придать другую форму.
Направим ось 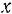
обращается о тождество и отпадает.
Остаются два уравнения
причем центры 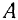
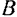
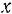
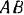
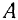
Для равновесия плоской системы параллельных сил необходимо и достаточно, чтобы порознь равнялись нулю суммы алгебраических величин моментов всех сил относительно каждой из двух произвольно выбранных, но не лежащих на прямой, параллельной данным силам, точек плоскости:
Пример задачи:
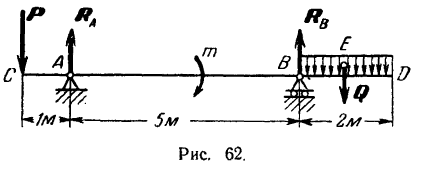
На двухконсольную горизонтальную балку действует пара сил с моментом 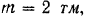
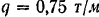
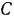
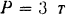
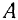
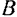
Решение:
Для определения реакций опор заменим распределенную нагрузку, действующую на участке балки длиной 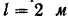
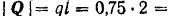
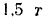
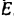
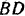
Реакция 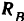
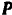
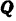
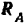
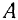
Составляем уравнения (30) равновесия балки. Так как (стр. 74) сумма алгебраических величии моментов сил пары относительно любого центра равна моменту пары и данная пара вращает плоскость чертежа по часовой стрелке, то
Полученный результат можно проверить. Так как балка находится в равновесии, то уравнение
должно обращаться при подстановке в него значений приложенных к балке сил в тождество. Действительно,
Силы пары в это уравнение мы не подставляем, так как алгебраическая сумма их всегда равна нулю.
Пример задачи:
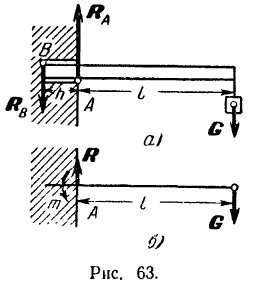
Балка заложена в стену на глубину 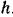
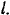
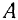
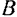
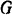
Решение:
Как видно из рис. 63, а, приложенная к балке сила 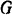
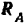
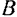
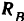
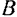
Составляя уравнения (30) равновесия для плоской системы параллельных сил, будем иметь:
Найденным реакциям стены в месте заделки можно придать и другую (рис. 63,6), часто применяемую форму, о которой было сказано выше (стр. 85). Так как
то реакцию 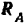
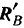
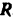
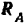
Силы 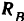
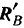
Этот момент, как видно из уравнения (II), равен но абсолютной величине моменту активной силы 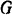
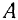
Он уравновешивает вращательный эффект приложенной к балке активной силы, т. е. препятствует вращению балки. Как видно из предыдущего равенства 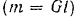
Реакция 
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Возможно вам будут полезны эти дополнительные темы:




















































Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
iSopromat.ru
Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:
Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.
Если система уравновешена, то получаем условия равновесия: R=0, MO=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:
Формы условий равновесия
Первая форма
Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:
причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.
Вторая форма
Уравнения равновесия могут быть записаны иначе:
Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.
Третья форма
Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.
Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.
Другие условия равновесия
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):
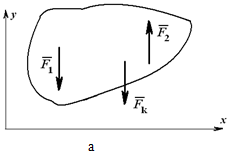
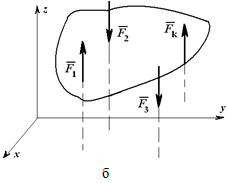
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:
Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:
и два уравнения для плоской системы:
В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Равновесие тела под действием пространственной системы сил
Содержание:
Для равновесия твердого тела, находящегося под действием произвольной пространственной системы сил,необходимо и достаточно, чтобы главный вектор этой системы сил и ее главный момент относительно произвольного центра О были равны нулю.
На странице -> решение задач по теоретической механике собраны решения задач и заданий с решёнными примерами по всем темам теоретической механики.
Условия равновесия тела, находящегося под действием пространственной системы произвольных сил
Поскольку любую пространственную систему произвольных сил можно свести к одной силе — главного вектора 



Причем, если 

Проекции главного вектора 
координат равны
Проекции главного момента на эти же оси координат равны
Далее, с учетом уравнений, выражение можно окончательно представить в виде уравнений равновесия тела под действием пространственной системы произвольных сил:
На основании этих уравнений состоят конкретные уравнения равновесия тела.
Таким образом, для равновесия тела, находящегося под действием пространственной
системы произвольных сил, необходимо и достаточно, чтобы алгебраические суммы
проекций всех сил на оси пространственной декартовой системы координат и
алгебраические суммы моментов всех сел относительно этих осей равны нулю.
Условия равновесия тела, находящегося под действием пространственной системы параллельных сил
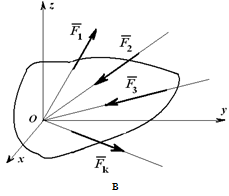
Если силы, приложенные к телу, расположенные в пространстве, но параллельны, то можно так выбрать систему координат, чтобы одна из осей (например, ось z) была параллельна данным силам (рис. 1.53). Тогда две другие оси (x, y) будут образовывать плоскость, которая будет перпендикулярной этим силам. Проекции заданных сил на оси x и y будут равны нулю. Как силы, параллельные оси, заданные силы не создают моментов относительно оси z.
Теперь, если принимать во внимание условия выше, то для пространственной системы параллельных сил три условия равновесия по данной системе выпадают, а остаются три другие. Итак, для равновесия пространственной системы параллельных сил имеем следующие уравнения равновесия:
Таким образом, для равновесия тела, находящегося под действием пространственной
системы параллельных сил, необходимо и достаточно, чтобы алгебраическая сумма
проекций всех сил на ось, которая параллельная силам, и алгебраические суммы
моментов относительно двух других осей равны нулю.
Теорема Вариньона о моменте равнодействующей силы относительно оси
Предположим, что есть тело, к которому приложена пространственная система
произвольных сил 




силу 

на одной прямой, но имеет противоположное направление.
В этом случае тело, которое находится под действием системы сил 




Найдем из этого выражения момент силы 
Поскольку модуль силы 





Такие условия можно составить в отношении двух других осей.
Таким образом, если пространственная система произвольных сил сводится к
равнодействующей, то момент равнодействующей силы относительно произвольной оси равен алгебраической сумме моментов составляющих сил относительно этой же оси.
Пример равновесия тела под действием пространственной системы произвольных сил
Есть горизонтальный вал трансмиссии (рис. 1.55), который несет два шкивы C и D ременной передачи и может вращаться в подшипниках A и B. Радиусы шкивов равны rC = 0,2 м, rD = 0,25 м. Натяжения ветвей ремня на шкиве C — горизонтальные 







Система находится в равновесии.
Определить натяжения 

Решение.
Рассмотрим равновесие вала AB со шкивами C и D. Освободим вал от связей, заменив их соответствующими реакциями. В подшипниках реакции расположены в плоскости, перпендикулярной оси вала AB. Таким образом, реакции подшипников A и B расположены соответственно в плоскости xAz и в плоскости, параллельной к ней и проходит через точку B. Неизвестный вектор каждой реакции подшипников в плоскости определяется двумя проекциями на оси x и z, как это показано на рис. 1.55. После сделанных
предположений, полученная пространственная система произвольных сил, находится в
состоянии равновесия.
Запишем на основании условий равновесия соответствующие уравнения равновесия пространственной системы произвольных сил.
Как видно из полученной системы уравнений равновесия, второе уравнение отсутствует, поскольку среди сил, приложенных к телу, нет таких, которые бы могли быть спроецированы на ось y (т. е. все силы лежат в плоскостях, перпендикулярных оси y). Однако, данная система является статически обозначенной, поскольку число неизвестных величин (t2, XA, ZA, XB, ZB) равно числу уравнений равновесия — 5.
Если подставить в данную систему уравнений числовые значения величин, заданные (учитывая, что по условию задачи 

Значения неизвестных величин XA и XB отрицательные, а это означает, что, фактически, эти реакции, которые показаны на рис. 1.55, имеют противоположное направление.
Для окончательного определения реакций подшипников в точках A и B необходимо добавить геометрически их составляющие. А именно
Услуги по теоретической механике:
Учебные лекции:
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
http://isopromat.ru/teormeh/obzornyj-kurs/uravnenia-ravnovesia-sistemy-sil
http://natalibrilenova.ru/ravnovesie-tela-pod-dejstviem-prostranstvennoj-sistemyi-sil/