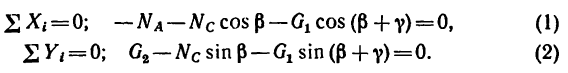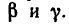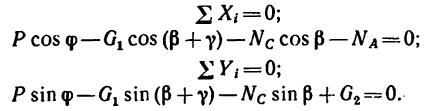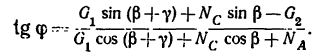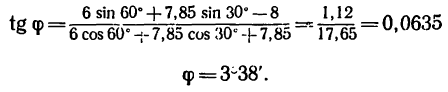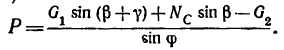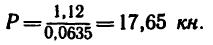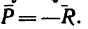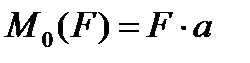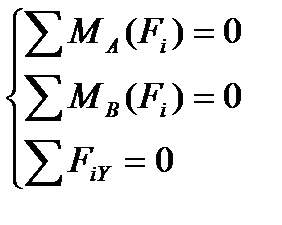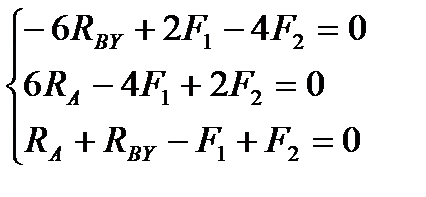Равновесие сходящихся сил в теоретической механике
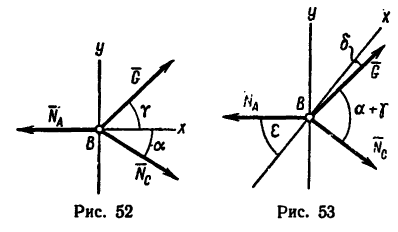
Равновесие сходящихся сил:
При определении равнодействующей системы пяти сил в задаче установлено, что
Из геометрического условия следует аналитическое условие равновесия, выражающееся двумя уравнениями:
Следует заметить, что все задачи, приведенные в § 6-2, можно решить с применением условия равновесия системы сходящихся сил. Причем при решении задач на равновесие системы сходящихся сил можно использовать те же три метода: графический, графо-аналитический и аналитический (метод проекций).
Необходимо учитывать, что если рассматривается равновесие плоской системы сходящихся сил, приложенных к одному телу, число неизвестных величин не должно превышать двух (условие статической определимости задачи с плоской системой сходящихся
сил):
- а) неизвестна одна сила, т. е. ее модуль и направление;
- б) неизвестны направления двух сил данной системы;
- в) неизвестны модуль одной из сил и направление второй;
- г) неизвестны модули двух сил.
При графическом методе решения во всех четырех случаях можно построить замкнутый силовой многоугольник и найти в нем неизвестные величины.
Графо-аналитический метод целесообразно применять в тех случаях, когда рассматривается равновесие трех сил. При этом по условию задачи в произвольном масштабе строится замкнутый треугольник, который затем решается на основе геометрических либо тригонометрических соотношений.
Метод проекций целесообразно применять для решения задач с числом сил больше трех.
При решении задач на равновесие плоской системы сходящихся сил рекомендуется придерживаться такой общей для всех систем схемы:
- а) выделить тело или точку, равновесие которых рассматривается в данной задаче, и изобразить их на рисунке;
- б) выяснить, какие нагрузки действуют на тело (точку) и также изобразить их на рисунке;
- в) освободить выделенное тело (точку) от связей и заменить их действие реакциями, которые надо изобразить на том же рисунке;
- г) на основе полученной схемы сил построить замкнутый силовой треугольник (если рассматривается равновесие трех сил) или составить уравнения равновесия; причем при составлении уравнений проекций оси целесообразно расположить так, чтобы их направления были параллельны или перпендикулярны к искомым силам (оси проекций также показываются на рисунке);
- д) после решения уравнений равновесия полученные результаты необходимо проверить либо при помощи неиспользованных уравнений или соотношений, либо путем решения задачи другим способом.
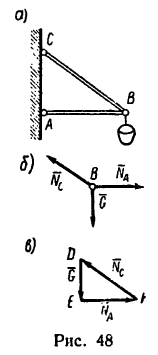
Задача №1
Фонарь весом 9 кГ подвешен на кронштейне АВС (рис. 48, а). Определить реакции горизонтального стержня АВ и наклонной тяги ВС, если АВ 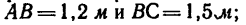
Решение —графо-аналитическим методом с применением геометрических соотношений.
1. В данном случае на шарнир В действуют три силы; вес фонаря G (рис. 48, 6) и реакции стержней 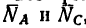
Заметим, что стержень АВ сжат, значит реакция 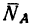
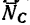
2. Так как шарнир В под действием этих трех сил находится в равновесии, силовой треугольник, составленный из них, должен быть замкнутым.
Выберем произвольную точку D (рис. 48, в) и отложим от нее отрезок DE, изображающий силу G. Из точек Е и D проведем прямые EF и DF, параллельные соответственно АВ и СВ. В полученном треугольнике DEF сторона EF изображает реакцию 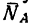
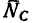
3. Так как в условии задачи даны линейные размеры кронштейна, величины сил 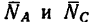
4. Неизвестную в задаче длину АС определяем по теореме Пифагора:
* Если все указанные в п. 2 построения выполнить в определенном масштабе, а затем измеренные длины FF и FD умножить на масштаб построения, то получим решение задачи графическим методом.
5. Окончательно
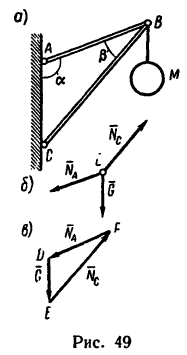
Задача №2
В точке В кронштейна АВС (рис. 49, а) подвешен груз М массой 816 кг. Определить реакции стержней кронштейна, если углы кронштейна 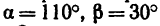
Решение 1— графоаналитическим методом с применением тригонометрических соотношений.
1. На точку В кронштейна действуют три силы: вес груза 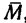
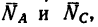
2. Так как эти три силы образуют уравновешенную систему, то составленный из них треугольник должен быть замкнутым (рис. 49, в — построение 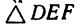
3. 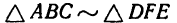
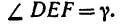
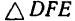
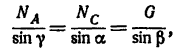
откуда
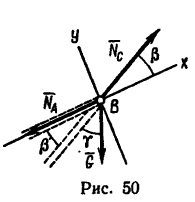
Решение 2—методом проекций при помощи уравнений равновесия.
1. Так как три силы 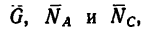
2. Выберем оси координат так, чтобы одна из осей совпадала с линией действия одной из неизвестных сил (см. рис. 50), и составим два уравнения проекций:
Как видно, ответ получается тот же.
После решения задач, аналогичных 39-8 и 40-8, можно сделать ошибочный вывод, что силовой треугольник и треугольник, образованный стержнями кронштейна, должны быть подобными. Но это совсем не обязательно. В этом легко убедиться, рассмотрев следующую задачу.
Задача №3
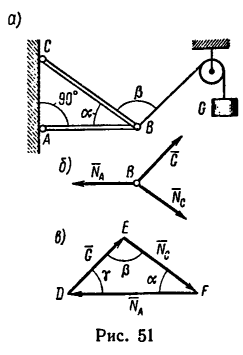
К шарниру В кронштейна АВС прикреплена веревка, перекинутая через блок, к другому концу которой прикреплен груз весом G= 1,5 кн (рис. 51. а).
Определить усилия в стержнях АВ и СВ кронштейна, если крепления в точках А и С шарнирные, а = 35° и 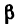
Решение 1-графо-аналитическим методом с применением тригонометрических соотношений.
1. На шарнир В в направлении к блоку действует натяжение веревки, равное весу груза G, и вызывает появление двух усилий, направленных вдоль стержней.
При этом стержень АВ растягивается, а стержень СВ сжимается.
Так как рассматривается равновесие шарнира В, то отбросим стержни, заменив их реакциями 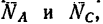
2. Силы G, 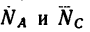
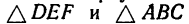
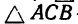
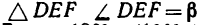
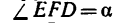
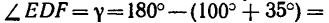
3. Применив к 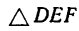
Решение 2—методом проекций.
1. Изобразив шарнир В вместе с действующими на него силами 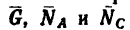
2. Из уравнения (2)
а из уравнения (1)
Как и следовало ожидать, оба решения дают одинаковый результат. Реакции стержней (их действия на шарнирный болт В) равны 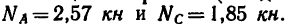
В связи с решением подобных задач методом проекций необходимо отметить следующее. Применяя метод проекций к определению равнодействующей любого числа сходящихся сил, наиболее удобно использовать обычную прямоугольную систему координатных осей. При этом найденные проекции равнодействующей и искомая равнодействующая образуют прямоугольный треугольник, решая который легко определить модуль и направление равнодействующей.
Применяя метод проекций к решению задач на равновесие сил, совсем не обязательно использовать взаимно перпендикулярные оси.
В тех случаях, когда определяются модули сил, направления которых заданы (как в задачах, каждую из осей целесообразно расположить перпендикулярно к направлению искомых сил. Тогда в каждое уравнение равновесия войдет только одно неизвестное.
Решим таким образом ту же задачу 41-8.
1. Изобразим шарнирный болт В с действующими на него силами (рис. 53).
Расположим ось х перпендикулярно 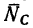
2. Замечая, что 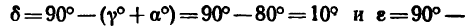
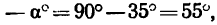
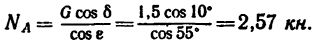
3. Расположим вторую ось (ось у) перпендикулярно к направлению силы 
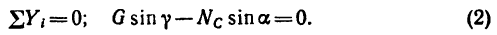
4. Из уравнения (2) 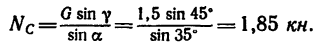
Возможность произвольного расположения осей проекций позволяет производить проверку решения задачи. Чтобы проверить правильность решения задачи, проведенного любым способом, следует выбрать расположение оси таким образом, чтобы на нее спроектировались обе найденные силы. При правильном решении сумма проекций на вновь выбранную ось получится равной нулю. Если же сумма не равна нулю, нужно искать допущенную в решении ошибку.
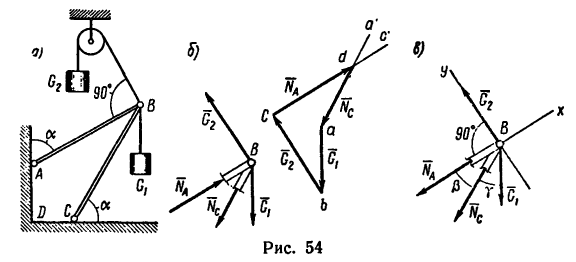
Задача №4
При помощи стержневого устройства АВС (в точках А, В и С соединения шарнирные) удерживаются в равновесии
два груза — первый весом 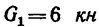
В этой задаче на шарнир В действуют уже не три, а четыре силы, поэтому решать задачу графо-аналитическим методом не имеет смысла — решение получится слишком длинным.
Когда на устройство, состоящее из двух стержней, действует одна нагрузка (как в задачах 38-8, 40-8 и 41-8), то можно легко определить, какой из стержней растянут и какой сжат.
В данной задаче это сразу определить нельзя, так как груз 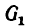
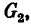
При решении задачи графическим методом направления усилий в стержнях определяют следующим образом.
Выбрав масштаб сил, из произвольной точки а построим отрезок ab, изображающий вектор 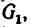
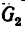
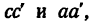
Получается замкнутый силовой четырехугольник abcd (рис. 54, б), в котором стороны cd и da изображают соответственно реакции 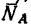
- 1) реакция
действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат;
- 2) реакция
действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.
При решении методом проекций нет необходимости заранее определять, в какую сторону направлены реакции вдоль стержней. Целесообразнее предположить, что под действием нагрузки все стержни растянуты (т. е. их реакции направлены от шарнира, равновесие которого рассматриваем, к стержням). Затем выбрать оси проекций, составить уравнения равновесия и решить их. У действительно растянутых стержней модули их реакций получатся положительными (предположительное направление реакций совпадает с действительным), а у сжатых стержней модули их реакций получатся отрицательными (предположительное направление реакций противоположно действительному).
Учитывая изложенное выше, приступим к решению задачи.
1. Изобразим шарнир В с действующими на него нагрузками 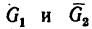
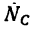
2. Совместим оси проекций с силами 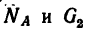
3. Прежде чем приступить к решению уравнений, нужно найти углы
Угол 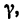
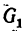
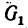
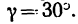
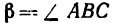
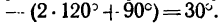
4. Из уравнения (2) 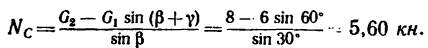
Таким образом, стержень ВС растянут силой 5,60 кн. Из уравнения (1)
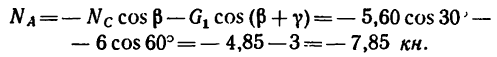
Следовательно, стержень АВ сжат силой 7,85 кн.
Задача №5
Каждую силу Р нужно дополнительно приложить к шарниру В стержневого устройства, описанного в задаче 42-8, чтобы оба стержня АВ и СВ были растянуты усилиями 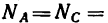
1. Используя рис. 54, айв, изобразим шарнир В с действующими на нем силами 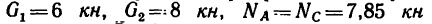
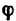
2. Составим уравнения равновесия:
3. В каждое из уравнений входят обе неизвестные величины — модуль силы 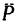
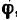
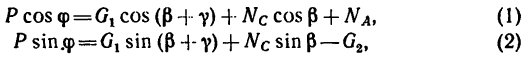
а потом уравнение (2) разделить на уравнение (1):
Отсюда
4. Подставив найденное значение угла 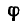
Из уравнения (2)
Так как числитель этого выражения определен в п. 3 и равен 1,12, а знаменатель 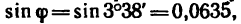
Таким образом, для того чтобы оба стержня были растянуты с одинаковыми усилиями по 7,85 кн, к шарниру В необходимо добавить силу 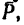
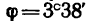
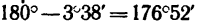
Задачу 43-8 можно было решить по примеру задач, приведенных в § 7-2. Для четырех заданных сил 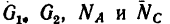
| Рекомендую подробно изучить предмет: |
|
| Ещё лекции с примерами решения и объяснением: |
- Равновесие трех непараллельных сил
- Сочлененные системы
- Равновесие пространственной системы сходящихся сил
- Определение положения центра тяжести тела
- Обобщенные координаты системы
- Сложение двух сил
- Разложение силы на две составляющие
- Определение равнодействующей сходящихся сил
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Техническая механика
Плоская система сходящихся сил
Геометрический способ определения равнодействующей плоской системы сходящихся сил
Система сил, линии действия которых лежат в одной плоскости и все пересекаются в одной точке, называется плоской системой сходящихся сил.
Теорема
Плоская система сходящихся сил в общем случае эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих.
Пусть дана плоская система трех сил F1 , F2 и F3 , линии действия которых сходятся в точке А (см. рисунок а) .

R = F1 + F2 .
Пользуясь той же аксиомой параллелограмма, сложим равнодействующую R с силой F3 :
где FΣ – равнодействующая данной системы трех сил.
Аналогичные рассуждения можно провести для любого количества сходящихся сил, в результате чего получим:
FΣ = F1 + F2 + F3 +…+ Fn .
Сокращенно это равенство можно записать так:
FΣ = ΣFi , где i – все целые числа от единицы до n .
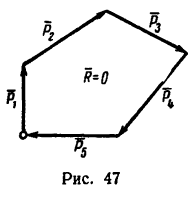
Очевидно, что построения, выполненные на рисунке a , можно заменить более простым, как показано на рисунке b . Многоугольник АВСD называют силовым многоугольником. Сторона AD , соединяющая начало первого с концом последнего вектора, называется замыкающей стороной.
Необходимо помнить, что стрелки векторов слагаемых сил образуют определенное направление обхода по контуру силового многоугольника, а замыкающая сторона, определяющая модуль и направление равнодействующей, имеет стрелку, направленную против обхода (см. рисунок b) .
Если определить равнодействующую из силового многоугольника с помощью геометрии и тригонометрии, то такой способ будет называться геометрическим.
Если сделать чертеж силового многоугольника в определенном масштабе, то равнодействующая определится простым измерением замыкающей стороны с последующим умножением на масштаб. Такой способ нахождения равнодействующей называется графическим.
Порядок сложения векторов при построении силового многоугольника на величину равнодействующей не влияет, так как векторная сумма от перемены мест слагаемых не меняется.
Геометрическое условие равновесия плоской системы сходящихся сил
При построении силового многоугольника возможен случай, когда конец последнего вектора совпадает с началом первого. В этом случае замыкающей стороны не будет, и такой силовой многоугольник называется замкнутым.
Очевидно, что равнодействующая FΣ системы сходящихся сил, образующих замкнутый силовой многоугольник, равна нулю, т. е. система сил находится в равновесии. Отсюда вытекает условие, при котором плоская система сходящихся сил будет находиться в равновесии. Это условие выражается равенством:
и формулируется так: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник был замкнут.
Условия равновесия, записанные в виде равенств, содержащих неизвестные величины, называются уравнениями равновесия.
Применяя геометрическое условие равновесия, удобно решать задачи, в которых на тело действуют три силы, так как в этом случае замкнутый силовой многоугольник представляет собой треугольник.
Решение большинства задач статики проводят в три этапа:
— выбирают тело, равновесие которого будет рассматриваться;
— отбрасывают связи, заменяя их реакциями, и устанавливают, какая система сил действует на тело;
— пользуясь условиями равновесия, находят неизвестные величины.
При решении задач статики следует строго соблюдать правило: размерности и единицы величин всех слагаемых и обеих частей равенства должны быть одинаковыми.
В сомнительных случаях целесообразно использовать это правило для проверки правильности хода решения задач, для чего следует подставить в слагаемые проверяемого равенства единицы всех входящих в них величин и, произведя возможные сокращения, сравнить полученные единицы правой и левой частей.
Пример решения задачи
В качестве примера решения задачи с использованием изложенных выше методов, определим натяжение веревки F и силу давления шара P на стену, если сила тяжести шара равна G .
Рассмотрим условие равновесия шара. Применив принцип освобождаемости, отбросим связи и заменим их реакциями. Реакция N гладкой стены перпендикулярна стене и проходит через центр шара (так как шар однородный, его геометрический центр совпадает с центром тяжести).
Реакция F веревки направлена вдоль линии натяжения веревки и тоже проходит через центр шара (согласно теореме о равновесии трех непараллельных сил). Применим к системе сил уравнение равновесия:
ΣFi = 0 , или G + N + R = 0.
Строим замкнутый силовой треугольник, начиная с изображения в произвольном масштабе вектора известной силы G (см. рисунок) . Направление обхода треугольника (т. е. направление стрелок) определяется направлением этой силы. Из построенного силового треугольника получим соотношения:
N = G tg α ; R = G/cos α
Искомая сила давления P шара на стену, согласно аксиоме взаимодействия, по модулю равна реакции N стены, но направлена в противоположную сторону.
Натяжение веревки F равно по модулю ее реакции R .
Эту же задачу можно решить, разложив силу тяжести шара G по реальным направлениям (направлениям реакций) на составляющие P (сила давления шара на стену) и F (натяжение веревки) , причем согласно аксиоме взаимодействия:
Из построенного параллелограмма (см. рисунок) легко определить искомые величины.
Такой метод решения задачи называют методом разложения силы.
Проекция силы на оси координат
В тех случаях, когда на тело действует более трех сил, а также когда неизвестны направления некоторых сил, удобнее при решении задач пользоваться не геометрическим, а аналитическим условием равновесия, которое основано на методе проекций сил на оси координат.
Проекцией силы на ось называют отрезок оси, заключенный между двумя перпендикулярами, опущенными на ось из начала и конца вектора силы.
На приведенном ниже рисунке видно, что проекции силы P на оси x и y можно определить при помощи тригонометрических функций:
Px = Pcos α, Py = Psin α .
Проекция силы на ось есть величина алгебраическая, которая может быть положительной или отрицательной, что устанавливается по направлению проекции — проекция, направленная в положительном направлении оси считается положительной, в противном случае — отрицательной.
Возможны два частных случая:
— если сила перпендикулярна оси, то ее проекция равна нулю (сила проецируется в точку) ;
— если сила параллельна оси, то она проецируется на ось в натуральную величину.
Зная проекции силы на координатные оси, можно определить ее величину (модуль) , используя теорему Пифагора, учитывая, что проекции являются катетами прямоугольного треугольника, а сама сила — гипотенузой.
Направляющий тангенс угла между вектором силы P и осью x можно определить из отношения:
tgα = Py/Px .
Отметим, что силу P можно представить, как равнодействующую двух составляющих сил Px и Py , параллельных осям координат, но эти составляющие не будут являться проекциями силы по определению, поскольку сила (в т. ч. и составляющая силы) есть величина векторная, а проекция — алгебраическая.
Аналитический способ определения равнодействующей плоской системы сил
Пусть дана плоская система сходящихся сил F1, F2, F3, F4. Fn .
Равнодействующая этой системы FΣ = ΣFi .
В плоскости действия данной системы сил выберем ось координат и спроецируем данные силы и их равнодействующую на эту ось. Из математики известно свойство проекции векторной суммы, на основании которого можно утверждать, что проекция равнодействующей на ось равна алгебраической сумме проекций составляющих сил на ту же ось, т. е. FΣx = ΣFix .
Правую часть этого равенства можно представить упрощенно: FΣx = ΣX .
Для того чтобы определить равнодействующую любой плоской системы сходящихся сил, спроецируем их на оси координат x и y , алгебраически сложим проекции всех сил и найдем таким образом проекции равнодействующей:
Зная проекции, определим модуль и направление равнодействующей:
Модуль равнодействующей:
FΣ = √(FΣx 2 + FΣy 2 ) (здесь и далее √ — знак корня);
Направляющий тангенс угла между вектором FΣ и осью x :
Линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Аналитические условия равновесия плоской системы сходящихся сил
Если данная плоская система сходящихся сил находится в равновесии, то равнодействующая такой системы, а значит и проекции равнодействующей на оси координат равны нулю.
Математически это выражение можно записать так:
Учитывая, что FΣx = ΣX; FΣy = ΣY , получаем равенства, выражающие аналитические условия равновесия плоской системы сходящихся сил:
Формулируется это условие следующим образом: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций этих сил на каждую из двух координатных осей равнялась нулю.
С помощью уравнений равновесия можно определить два неизвестных элемента данной системы сил, например модуль и направление одной силы или модули двух сил, направления которых известны и т. п.
Выведенные условия равновесия справедливы для любой системы координат, но для упрощения расчетов рекомендуется оси координат по возможности выбирать перпендикулярными неизвестным силам, чтобы каждое уравнение равновесия содержало одно неизвестное.
Когда направление искомой силы неизвестно, ее можно разложить на две составляющие по заданным направлениям, обычно по направлениям координатных осей; по найденным двум составляющим легко определяется неизвестная сила.
Если при решении задач аналитическим способом искомая реакция получается отрицательной, то это означает, что действительное ее направление противоположно направлению, принятому при расчетах.
Методика решения задач плоской системы сходящихся сил
1. Число неизвестных в данных задачах не превышает двух.
2. Рассматриваем точку, находящуюся в равновесии.
3. Определяем наличие активных сил.
4. Освобождаемся от связей и заменяем их реакциями.
5. Выбираем оси координат и располагаем в этих осях имеющиеся активные и реактивные силы.
6. Решаем уравнения равновесия относительно неизвестных.
7. Выполняем проверку.


Решение.
I. Аналитическое решение
1. Освобождаемся от связей, заменяя их реакциями. Получаем систему трех сходящихся в точке О сил.
2. Выбираем систему координат хОу и составляем таблицу, уравнения равновесия.
| силы |  =0 =0 |  =0 =0 |
| R1 |  |  |
| R2 |  |  |
| F1 |  |
3. Составляем систему уравнения и решаем.
Проверка: 


II. Графическое решение.
1. Выбираем масштаб 1:20 и из точки О откладываем вектор силы тяжести F1.
2. Полученная система сил находится в равновесии, поэтому силовой многоугольник должен быть замкнут, R1+R2+F1=0. Поэтому, из конца и начала вектора F проводим прямые параллельные векторам R1 и R2 до их пересечения.
3. Определяем реакции связей R1 и R2 , умножая полученные результате графического построения отрезки на масштаб.
4. Проверка: Заключается в сравнении значений векторов R1 и R2 , найденных аналитическим и графическим способами. r1 = (R1а — R1б)/ R1а; r1 = (R2а — R2б)/ R2а;
Задания для выполнения работы
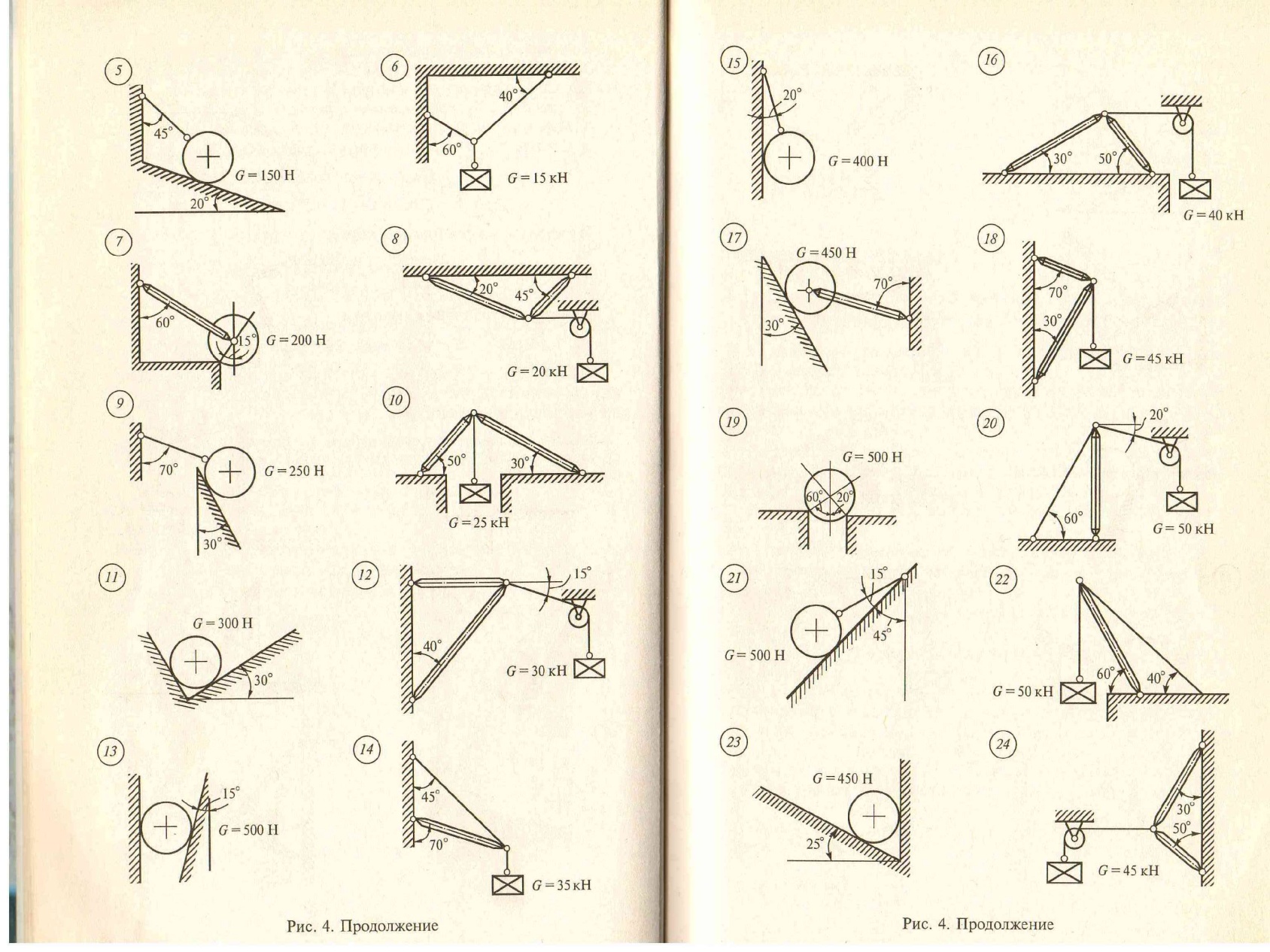
Груз, силой тяжести G удерживается в равновесии с помощью связей. Определить реакции связей, удерживающих груз аналитически и графически.
Контрольные вопросы:
1. В чем отличие между осью и проекцией?
2. Сколько уравнений равновесия Вы составляли при решении задачи?
3. Методика решения задач ПССС.
4. Дайте определение плоской системе сходящихся сил.
5. Какой величиной является проекция силы на координатную плоскость?
Литература:
1. Вереин Л.И. Техническая механика – М: Академия, 2006.
2. Мовнин М.С. Основы технической механики – СПБ: Политехника, 2003.
3. Молчанова Е.В., Шурыгина Г.Н. Статика и сопротивление материалов — Томск, 2008.
Практическая работа №3
Тема урока: Определение реакций в опорах с вертикальными нагрузками
Тип урока:закрепление полученных знаний.
Цель урока:Научиться определять реакции в опорах с вертикальными нагрузками
Обеспечивающие средства:
1. методическое руководство по выполнению работы;
3.тетрадь для практических работ;
4.карандаш, линейка, ластик, авторучка;
Технология работы:
1.Внимательно изучите методические указания, предложенный теоретический материал.
2.В соответствие с вариантом, выполнить задание по методике представленной ниже.
3.Сделайте выводы о проделанной работе.
4.Ответить на контрольные вопросы.
Теоретический материал


Момент –способность силы создавать вращение (М).
| Мо (F) = F * а |
Единица измерения М [ Н * м] 1кНм = 10 3 Нм, 1мНм = 10 6 Нм
Момент силы относительно точки равен произведению силы на перпендикуляр, опущенный из точки вращения на линию действия силы.
а – плечо, перпендикуляр или кратчайшее расстояние между точкой вращения и линией действия силы.


Момент силы относительно точки равен нулю, если линия действия силы проходит через точку вращения, т.к. плеча равно нулю, нет вращения.

Решение.
1. Определяем связи, заменяем их реакциями.
2. Определяем оси координат Х, У.
3. Составляем таблицу уравнения равновесия.

| Силы |  =0 =0 |  =0 =0 |  =0 =0  |
| RА | 6RA | RA | |
| RBY | -6RBY | RBY | |
| F1 | 2F1 | -4F1 | -F1 |
| F2 | -4F2 | 2F2 | F2 |
4. Составляем уравнение по II-ому виду
Из 1-го уравнения находим RBY
Из 2-го уравнения находим RA
5. Проверка: по 3-му уравнению 4,7+1,3-8+2=0
http://k-a-t.ru/tex_mex/11-statika_plosk_sily/
http://megalektsii.ru/s30619t3.html
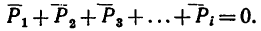
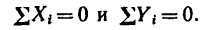
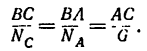
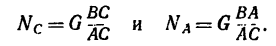
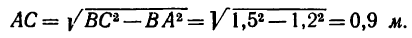
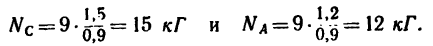

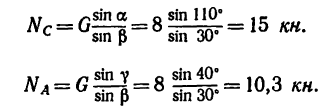
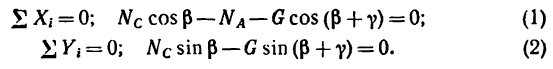
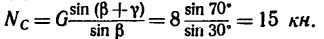
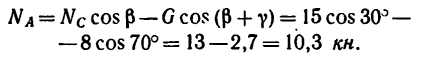
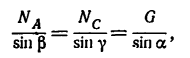
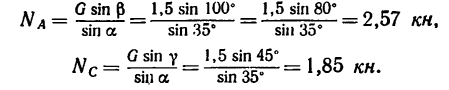
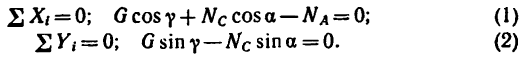
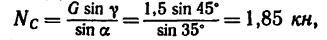
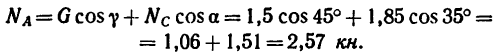
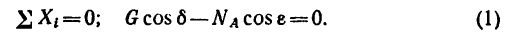
 действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат;
действует на шарнир в направлении от стержня к шарниру — значит стержень АВ сжат;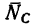 действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.
действует на шарнир в направлении от шарнира к стержню —значит стержень СВ растянут.