Уравнение равновесия пространственной произвольно расположенной сил

iSopromat.ru

Рассмотрим равновесие пространственной системы сил в аналитической и геометрической форме:

Произвольной пространственной системой сил называется система сил, линии действия которых не лежат в одной плоскости.

Согласно основной теореме статики (теореме Пуансо) любую произвольную систему сил, действующую на твердое тело, можно заменить эквивалентной системой, состоящей из силы (главного вектора системы) и пары сил (главного момента системы сил).

В геометрической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы главный вектор и главный момент системы равнялись нулю

В аналитической форме: для равновесия произвольной пространственной системы сил необходимо и достаточно, чтобы суммы проекций всех сил на три координатные оси и суммы моментов всех сил относительно этих осей были равны нулю

Условия равновесия могут быть использованы для решения задач на равновесие при определении неизвестных величин (реакций связей).

Чтобы задача была статически определимой, число неизвестных должно быть не более шести.

В частности, для системы параллельных сил условиями равновесия являются следующие равенства

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

Равновесие произвольной пространственной системы сил – решение задачи

Порядок решения задач на равновесие с произвольной пространственной системой сил

Чтобы решить задачу на равновесие твердого тела с произвольной пространственной системой сил, надо выбрать прямоугольную систему координат и, относительно нее, составить уравнения равновесия.

Уравнения равновесия, для произвольной системы сил, распределенных в трехмерном пространстве, представляют собой два векторных уравнения:
векторная сумма сил, действующих на тело, равна нулю
(1) ;
векторная сумма моментов сил, относительно начала координат, равна нулю
(2) .

Пусть Oxyz – выбранная нами система координат. Спроектировав уравнения (1) и (2) на оси этой системы, получим шесть уравнений:
суммы проекций сил на оси xyz равны нулю
(1.x) ;
(1.y) ;
(1.z) ;
суммы моментов сил относительно осей координат равны нулю
(2.x) ;
(2.y) ;
(2.z) .
Здесь мы считаем, что на тело действуют n сил, включая силы реакций опор.

Пусть произвольная сила , с компонентами , приложена к телу в точке . Тогда моменты этой силы относительно осей координат определяются по формулам:
(3.x) ;
(3.y) ;
(3.z) .

Таким образом, порядок решения задачи, на равновесие с произвольной пространственной системой сил, следующий.

1. Отбрасываем опоры и заменяем их силами реакций. Если опорой является стержень или нить, то сила реакции направлена вдоль стержня или нити.
2. Выбираем прямоугольную систему координат Oxyz .
3. Находим проекции векторов сил на оси координат, , и точек их приложения, . Точку приложения силы можно перемещать вдоль прямой, проведенной через вектор силы. От такого перемещения значения моментов не изменятся. Поэтому выбираем наиболее удобные для расчета точки приложения сил.
4. Составляем три уравнения равновесия для сил (1.x,y,z).
5. Для каждой силы, по формулам (3.x,y,z), находим проекции моментов силы на оси координат.
6. Составляем три уравнения равновесия для моментов сил (2.x,y,z).
7. Если число переменных больше числа уравнений, то задача статически неопределима. Методами статики ее решить нельзя. Нужно использовать методы сопротивления материалов.
8. Решаем полученные уравнения.

Упрощение расчетов

В некоторых случаях удается упростить вычисления, если вместо уравнения (2) использовать эквивалентное условие равновесия.
Сумма моментов сил относительно произвольной оси AA′ равна нулю:
(4) .

То есть можно выбрать несколько дополнительных осей, не совпадающих с осями координат. И относительно этих осей составить уравнения (4).

Далее приводится пример, в котором удается упростить вычисления за счет соответствующего выбора осей.

Пример решения задачи на равновесие произвольной пространственной системы сил

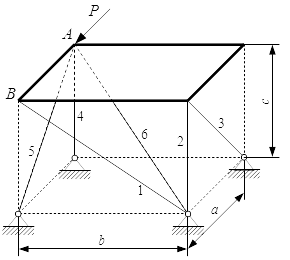
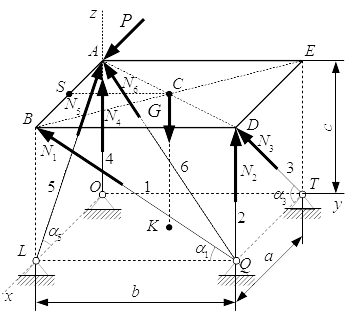
Найти реакции стержней, поддерживающих тонкую однородную горизонтальную плиту в трехмерном пространстве. Система крепления стержней показана на рисунке. На плиту действуют: сила тяжести G; и сила P, приложенная в точке A, направленная вдоль стороны AB.

Дано:
G = 28 kН ; P = 35 kН ; a = 7,5 м ; b = 6,0 м ; c = 3,5 м .

Решение задачи

Сначала мы решим эту задачу стандартным способом, применимым для произвольной пространственной системы сил. А затем получим более простое решение, основываясь на конкретной геометрии системы, за счет выбора осей при составлении уравнений равновесия.

Решение задачи стандартным способом

Этот метод хоть и приведет нас к довольно громоздким вычислениям, но он применим для произвольной пространственной системы сил, и может применяться в расчетах на ЭВМ.

Отбросим связи и заменим их силами реакций. Связями здесь являются стержни 1–6. Вводим вместо них силы , направленные вдоль стержней. Направления сил выбираем наугад. Если мы не угадаем с направлением какой-либо силы, то получим для нее отрицательное значение.

Проводим систему координат Oxyz с началом в точке O .

Находим проекции сил на оси координат.

Для силы имеем:
.
Здесь α ₁ – угол между LQ и BQ . Из прямоугольного треугольника LQB :
м ;
;
.

Силы , и параллельны оси z . Их компоненты:
;
;
.

Для силы находим:
.
Здесь α ₃ – угол между QT и DT . Из прямоугольного треугольника QTD :
м ;
;
.

Для силы :
.
Здесь α ₅ – угол между LO и LA . Из прямоугольного треугольника LOA :
м ;
;
.

Сила направлена по диагонали прямоугольного параллелепипеда. Она имеет следующие проекции на оси координат:
.
Здесь – направляющие косинусы диагонали AQ :
м ;
;
;
.

Выбираем точки приложения сил. Воспользуемся тем, что их можно перемещать вдоль линий, проведенных через векторы сил. Так, в качестве точки приложения силы можно взять любую точку на прямой TD . Возьмем точку T , поскольку для нее x и z — координаты равны нулю:
.
Аналогичным способом выбираем точки приложения остальных сил.

В результате получаем следующие значения компонентов сил и точек их приложений:
; (точка B );
; (точка Q );
; (точка T );
; (точка O );
; (точка A );
; (точка A );
; (точка A );
; (точка K ).

Составляем уравнения равновесия для сил. Суммы проекций сил на оси координат равны нулю.

;

;

.

Составляем уравнения равновесия для моментов сил. Суммы моментов сил относительно осей координат равны нулю.

;

;

;

В этой системе шесть уравнений и шесть неизвестных. Далее сюда можно подставить численные значения и получить решение системы, используя математическую программу вычисления системы линейных уравнений.

Но, для этой задачи, можно получить решение без использования средств вычислительной техники.

Эффективный способ решения задачи

Мы воспользуемся тем, что уравнения равновесия можно составлять не единственным способом. Можно произвольным образом выбирать систему координат и оси, относительно которых вычисляются моменты. Иногда, за счет выбора осей, можно получить уравнения, которые решаются более просто.

Воспользуемся тем, что, в равновесии, сумма моментов сил относительно любой оси равна нулю. Возьмем ось AD . Сумма моментов сил относительно этой оси равна нулю:
(П7) .
Далее заметим, что все силы, кроме пересекают эту ось. Поэтому их моменты равны нулю. Не пересекает ось AD только одна сила . Она также не параллельна этой оси. Поэтому, чтобы выполнялось уравнение (П7), сила N ₁ должна равняться нулю:
N ₁ = 0 .

Теперь возьмем ось AQ . Сумма моментов сил относительно нее равна нулю:
(П8) .
Эту ось пересекают все силы, кроме . Поскольку сила не параллельна этой оси, то для выполнения уравнения (П8) необходимо, чтобы
N ₃ = 0 .

Теперь возьмем ось AB . Сумма моментов сил относительно нее равна нулю:
(П9) .
Эту ось пересекают все силы, кроме , и . Но N ₃ = 0 . Поэтому
.
Момент от силы относительно оси равен произведению плеча силы на величину проекции силы на плоскость, перпендикулярную оси. Плечо равно минимальному расстоянию между осью и прямой, проведенной через вектор силы. Если закручивание происходит в положительном направлении, то момент положителен. Если в отрицательном – то отрицательный. Тогда
.
Отсюда
kН .

Остальные силы найдем из уравнений (П1), (П2) и (П3). Из уравнения (П2):
N ₆ = 0 .
Из уравнений (П1) и (П3):
kН ;
kН

Таким образом, решая задачу вторым способом, мы использовали следующие уравнения равновесия:
;
;
;
;
;
.
В результате мы избежали громоздких расчетов, связанных с вычислениями моментов сил относительно осей координат и получили линейную систему уравнений с диагональной матрицей коэффициентов, которая сразу разрешилась.

N ₁ = 0 ; N ₂ = 14,0 kН ; N ₃ = 0 ; N ₄ = -2,3 kН ; N ₅ = 38,6 kН ; N ₆ = 0 ;

Знак минус указывает на то, что сила N ₄ направлена в сторону, противоположную той, которая указана на рисунке.

Автор: Олег Одинцов . Опубликовано: 13-11-2017

Техническая механика

Пространственная система сил

Пространственная система сходящихся сил

Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .

Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.

Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.

Пусть дана пространственная система n сходящихся сил (F₁, F₂, F₃. F_n) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:

Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .

Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.

Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.

Разложение силы по трем осям координат

Пусть дана сила F (см. рисунок 1) .
Возьмем систему координат так, чтобы начало координат совпадало с началом вектора силы F (т. е. с точкой приложения силы). Из конца этого вектора опустим перпендикуляр на плоскость xy и разложим силу F на составляющие F_xy и F_z , а составляющую F_xy – на составляющие F_x и F_y . Тогда:

Достроим полученное изображение до параллелепипеда, у которого составляющие F_x , F_y и F_z являются ребрами, а сила F – диагональю.

Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .

Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие F_x , F_y и F_z равны по модулю проекциям силы F на эти оси.

Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:

модуль силы: F = √(F_x 2 + F_y 2 + F_z 2 ) (здесь и далее √ — знак корня) ;

направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .

Аналитический способ определения равнодействующей пространственной системы сходящихся сил

Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.

Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:

Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.

Аналитические условия равновесия пространственной системы сходящихся сил

Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:

ΣX = 0; ΣY = 0; ΣZ = 0 .

Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.

Момент силы относительно оси

Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.

Разложим силу F на три взаимно-перпендикулярные составляющие F₁ , F₂ и F₃ .
Составляющую F₁ назовем окружной силой , составляющую F₂ – осевой силой , а составляющую F₃ – радиальной силой .
Из рисунка видно, что составляющая F₁ вызывает вращательное действие, которое измеряется произведением силы F₁ на радиус колеса r ; составляющая F₂ стремится сдвинуть червячное колесо вдоль оси, а составляющая F₃ стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F₂ и F₃ относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F₁ , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).

Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.

Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:

Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.

Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.

Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):

• если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила F_Z) ;
• если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F₃ на рисунке 2) .

Аналитические условия равновесия пространственной системы произвольно расположенных сил

Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.

Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.

Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.

Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:

• ΣX = 0; ΣMx(Fi) = 0;
• ΣY = 0; ΣMy(Fi) = 0;
• ΣZ = 0; ΣMz(Fi) = 0.

Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.

Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.

Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.

Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)

Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .

Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил F_Σ (см. рисунок 4) :

Приложим к телу другую систему сил, равнодействующая которой F’_Σ по модулю равна F_Σ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:

Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например

Запишем это условие для обеих систем:

Так как правые части этих равенств равны, то будут равны и левые :

Сократив общее слагаемое M_x(F’_Σ) , получим: