Уравнение равновесия системы произвольно расположенных сил

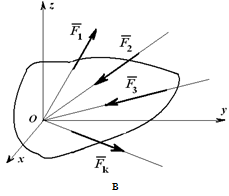
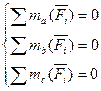ТЕМА 7.РАВНОВЕСИЕ СИСТЕМЫ ПРОИЗВОЛЬНО РАСПОЛОЖЕННЫХ СИЛ

Теорема Вариньона. О моменте равнодействующей.

Момент равнодействующей силы относительно любой точки на плоскости равен алгебраической сумме моментов сил составляющих относительно той же точки.

Например, требуется определить момент силы R относительно точки А (рис. 29).

Раскладываем силу на две составляющие F₁ и F₂ и на основании теоремы Вариньона

Аналогично эта теорема используется и в пространстве: момент равнодействующей силы, относительно любой оси равен алгебраической сумме момент составляющих сил относительно этой оси.

Условия равновесия плоской системы произвольно расположенных сил.

Для сил произвольно расположенных на плоскости условиями равновесия будут равенство нулю главного вектора и главного момента R*=O; М=O.

Эти условия выражаются в виде трех уравнений равновесия.

Это основные уравнения равновесия.

Существуют и другие системы уравнений равновесия:

При этом ось U не должна быть перпендикулярна прямой проходящей через точки А и В.

Точки А,В и С не должны находиться на одной прямой.

Условия равновесия пространственной системы произвольно расположенных сил.

Случаю равновесия сил, произвольно расположенных в пространстве, как и на плоскости соответствуют два условия равновесия:

Но в пространстве им соответствует шесть уравнений равновесия: три уравнения проекции сил на оси декартовых координат и три уравнения моментов сил относительно этих осей:

Существуют также другие системы

МОДУЛЬ 2

В кинематике изучается движение материальных объектов (точки, твердого тела, сплошной среды) без рассмотрения причин, вызывающих или изменяющих это движение. Такое изучение движения материальных объектов не требует учета материальных характеристик этих объектов — массы, моментов инерции и др. В кинематике рассматривают такие характеристики движе­ния, как скорость и ускорение точки, угловые скорость и ускорение твердого тела и др.

Движение материального объекта всегда следует рассматри­вать относительно какого-либо твердого тела — тела отсче­та, т.е. движение, является относительным. С телом отсчета скрепляют систему осей координат, например декарто­вых, принимая ее за систему отсчета, относительно которой рассматривается движение материального объекта.

Независимость времени от движения означает, что во всех системах отсчета, произвольно движущихся друг относительно друга, оно одно и то же, если за начало отсчета выбрано общее для них событие.

В курсе теоретической механики обычно изучаются движение точки и твердого тела. Соответственно кинематика делится на кинематику точки и кинематику твердого тела. В настоящем курсе дополнительно излагаются также основы кинематики сплошной среды.

ТЕМА 8.КИНЕМАТИКА ТОЧКИ

В кинематике точки рассматриваются характеристики движе­ния точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важ­ным в кинематике точки является понятие траектории. Траекторией точки называется геометрическое место ее последова­тельных положений в пространстве с течением времени относи­тельно рассматриваемой системы отсчета.

По виду траекторий движения точки делятся на прямо­линейные и криволинейные. Форма траектории зависит от выбранной системы отсчета. Одно и то же движение точки может быть прямолинейным относительно одной системы отсчета и криволинейным относительно другой. Например, если с летящего горизонтально Земле с постоянной скоростью самолета отцеплен груз, то, пренебрегая сопротивлением воздуха и учитывая только действие силы тяжести, получим в качестве траектории движения центра масс груза от­носительно самолета прямую линию, а относительно Земли — параболу.

Скорость точки

Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы коорди­нат (рис. 1).

Положение движущейся точки М относительно рассматри­ваемой системы отсчета определяется в момент времени t радиусом-вектором r, который соединяет неподвижную точку О с этой точкой. В другой момент времени t₁ =t +∆t движущаяся точка займет положение М₁ и ее радиус-вектором будет r_1. За время ∆t радиус-вектор движущейся точки изменится на ∆ r= r₁ — r₁

Средней скоростью V_ср точки за время ∆t называют отношение ∆r /∆t т. е. Введем скорость точки v в момент t, которая определяется V=dr/dt

Таким образом, скорость точки равна первой производной по времени от ее радиус-вектора. Она направлена по касательной к траектории в сторону движения точки. Размерность скорости в СИ: [v ] = длина/время = м/с.

Часто скорость выражают в км/ч; км/ч = 3,6 v м/с.

Ускорение точки

Пусть движущаяся точка М в момент времени t имеет скорость v. В момент времени t₁ = t + ∆t эта точка занимает положение М₁, имея скорость v₁ (рис.2, а). Чтобы изобразить приращение скорости ∆v за время ∆t, перенесем вектор скорости v₁ параллельно самому себе в точку М.

Средним ускорением точки а_ср за время ∆t называют отношение ∆v/∆t, т. е. a_cp = ∆v/∆t. Среднее ускорение точки параллельно приращению скорости ∆v. Как и средняя скорость, среднее ускорение не имеет на траектории конкретной точки приложения и изображено в точке М условно. В общем случае среднее ускорение зависит от времени ∆t.

Таким образом, ускорение точки равно первой производной по времени от скорости точки.

Приращение скорости ∆v и, следовательно, среднее ускоре­ние направлены внутрь вогнутости траектории. Так же направ­лены и их предельные значения при ∆t, стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории

Размерность ускорения в СИ получаем из (2): [а]= [v ] / [t ] = скорость/время = м/с 2 = м • с -2 .

iSopromat.ru

Рассмотрим условия равновесия произвольной плоской и пространственной систем сил, включая три основные формы и частные случаи равновесия для систем параллельных и сходящихся сил:

Из основной теоремы статики следует, что любая система сил и моментов, действующих на твердое тело, может быть приведена к выбранному центру и заменена в общем случае главным вектором и главным моментом.

Если система уравновешена, то получаем условия равновесия: R=0, M_O=0. Из этих условий для пространственной системы сил получается шесть уравнений равновесия, из которых могут быть определены шесть неизвестных:

Формы условий равновесия

Первая форма

Для плоской системы сил (например, в плоскости Oxy) из этих уравнений получаются только три:

причем оси и точка O, относительно которой пишется уравнение моментов, выбираются произвольно. Это первая форма уравнений равновесия.

Вторая форма

Уравнения равновесия могут быть записаны иначе:

Это вторая форма уравнений равновесия, причем ось Ox не должна быть перпендикулярна линии, проходящей через точки A и B.

Третья форма

Это третья форма уравнений равновесия, причем точки A, B и C не должны лежать на одной прямой.

Предпочтительность написания форм уравнений равновесия зависит от конкретных условий задачи и навыков решающего.

Другие условия равновесия

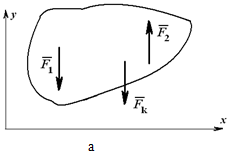
При действии на тело плоской системы параллельных сил одно из уравнений исчезает и остаются два уравнения (рисунок 1.26, а):

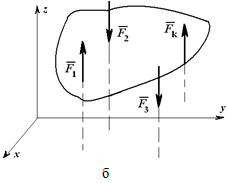
Для пространственной системы параллельных сил (рисунок 1.26, б) могут быть записаны три уравнения равновесия:

Для системы сходящихся сил (линии действия которых пересекаются в одной точке) можно написать три уравнения для пространственной системы:

и два уравнения для плоской системы:

В каждом из вышеприведенных случаев число неизвестных, находимых при решении уравнений, соответствует числу записанных уравнений равновесия.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

ПроСопромат.ру

Технический портал, посвященный Сопромату и истории его создания

Уравнения равновесия плоской системы сил

Всякая система произвольно расположенных в плоско­сти сил может быть приведена к главному вектору и глав­ному моменту (см. — здесь).

Для равновесия системы сил, произвольно рас­положенных в плоскости, необходимо и достаточно, чтобы главный вектор и главный момент этих сил относительно любого центра каждый в отдельности равнялся нулю.

Главный вектор представляет собой геометрическую сумму всех сил, составляющих систему и перенесенных в центр приведения. Величину главного вектора можно определить через проекции на координатные оси всех сил системы.

Для равновесия необходимо, чтобы главный вектор был равен нулю.

Кроме того, для равновесия необходимо, чтобы глав­ный момент также был равен нулю.

Таким образом, имеем уравнения:

ΣP_x = 0 (сумма проекций всех сил на ось X равна 0);

ΣP_y = 0 (сумма проекций всех сил на ось Y равна 0);

ΣM_o =0 (сумма моментов относительно любой точки равна 0)

Данные уравнения являются уравнениями равно­весия тела, находящегося под воздействием системы сил, произвольно расположенных в плоскости.