Уравнение регрессии без свободного члена

Особенности регрессии, проходящей через начало координат

Автор работы: Пользователь скрыл имя, 22 Декабря 2013 в 05:57, реферат

Краткое описание

Обнаружив взаимосвязь между двумя переменными, оценив интенсивность данной связи при помощи какого-нибудь коэффициента, исследователь пытается проинтерпретировать такую взаимосвязь по причинам и следствиям. Другими словами, конечным итогом измерений взаимосвязи между переменными считается подтверждение (либо опровержение) каких-нибудь содержательных предположений, которые касаются причинного механизма, рождающего выявленную взаимосвязь. Однако само по себе наличие связей между двумя переменными не доказывает, что данная связь может описываться моделью «причина — следствие».

Содержание

Введение………………………………………………………………………..…3
1 Особенности регрессии, проходящей через начало координат………………………………………………………………………. 4
Влияние на коэффициенты регрессии масштаба измерения переменных………………………………………………………………………..7
Заключение……………………………………………………………………….10
Список использованной литературы…………………………………………..12

Прикрепленные файлы: 1 файл

эконометрика.docx

1 Особенности регрессии, проходящей через начало координат……………………………………………………… ………………. 4

1. Влияние на коэффициенты регрессии масштаба измерения переменных…………………………………………………… …………………..7

Список использованной литературы…………………………………………..12

Обнаружив взаимосвязь между двумя переменными, оценив интенсивность данной связи при помощи какого-нибудь коэффициента, исследователь пытается проинтерпретировать такую взаимосвязь по причинам и следствиям. Другими словами, конечным итогом измерений взаимосвязи между переменными считается подтверждение (либо опровержение) каких-нибудь содержательных предположений, которые касаются причинного механизма, рождающего выявленную взаимосвязь. Однако само по себе наличие связей между двумя переменными не доказывает, что данная связь может описываться моделью «причина — следствие».

Термин «регрессия» впервые в статистике был использован Френсисом Гальтоном в 1886 из-за исследований вопросов наследований физическ их человеческих характеристик. В качестве одной из них был взят рост; при этом было выявлено, что в общем сыновья высоких отцов, оказались более высокими, в отличие от сыновей отцов с низким ростом. Более интересным стало то, что разброс роста сыновей был меньше, чем разброс роста отцов. Так проявлялась тенденция о возвращении роста сыновей к среднему росту (regression to mediocrity), или «регресс».

Регрессией в теории вероятностей, математической статистике, называется зависимость среднего значения какой-нибудь величины от некоторой иной величины либо от нескольких величин. В отличии от чисто функциональной зависимости y=f(x), когда для каждого значения независимой переменной x существует одно лишь определённое значение величин y, при регрессионной связи значению x могут соответствовать исходя из случая разные значения величины y.

1. Особенности регрессии, проходящей через начало координат

При помощи регрессионного анализа изучается эффект влияния одного признака на иной, зависимость этого признака от фактора и результативного признака от факториального. Основные результаты его следующие:

1. Построение таблицы с дисперсионным анализом, в которой показана сила, достоверность влияний на признак по изучаемому фактору либо другому признаку (таблица разложений общий варьирований результативного признака по компонентам и их соотнесение друг с другом).
2. Построение уравнения регрессии, которое выражает пропорциональность сопряженного изменения всех признаков, тенденции взаимосвязанной их изменчивости либо динамики.

3. Оценка значимости параметров в регрессионном уравнении.
Регрессионный анализ односторонне методически ориентирован на изучение зависимостей одного признака от другого (зависимость x от y или y от x), хоть и может применяться к тем случаям, когда имеется фактически взаимозависимость по двум переменным. Обобщенная зависимость, в свою очередь, исследуется при помощи «симметричного» метода – корреляционного анализа.

Говорить о том, как изменяется один показатель по мере изменений другого, помогает коэффициент регрессии (a), который показывает, на какую величину изменяется в среднем один признак (y), когда изменяется другой (x) на единицу измерения.

Форма — без свободного члена – может быть записана в следующем виде:

где Z — N´(n+1)-матрица, ее последний столбец состоит из единиц (равен 1_N);

a — (n+1)-это вектор-столбец, его последний элемент является свободным членом регрессии.

Оператор МНК-оцениваний для уравнения без свободного члена записывается более компактно так:

но — (n+1)´(n+1)-это матрица вторых начальных моментов [z, 1];

— (n+1)-это вектор-столбец вторых начальных моментов между x и [z,1] .

Если в этом операторе вернуться к обозначениям других форм уравнений регрессии, то получится выражение:

по которому видно, что

— обратная матрица ковариаций z (размерности N´N) аналогична соответствующему блоку обратной матрицы вторых начальных моментов (размерности (N+1)´(N+1));

— результаты от применений двух приведенных операторов оцениваний одинаковы.

Рассмотрим задачу по прямой без свободного члена, то есть прямой, которая проходит через начало координат и задается уравнением

Найдем оценку параметра при помощи метода наименьших квадратов, которая находится при решении экстремальной задачи

Критическая точка функции S определяется по условию

Следовательно, OLS-оценка коэффициента находится по формуле

Необходимо заметить, что прямая y = не всегда может проходить через точку (ẋ;ẏ), но она всегда проходит через точку начала координат.

Уравнение прямой без использования свободного члена применяется в некоторых прикладных задачах. К примеру, данная модель может использоваться при исследовании зависимостей прибыли от величины налога на прибыль.

Рассмотрим модель регрессии

где значения x считаются неслучайными или детерминированными величинами, y и ошибки случайными величинами. Относительно ошибок регрессии предполагается выполнение условий из парной регрессии с имеющейся константой. Тогда видно, что

Теорема (Гаусс – Марков). Зададим условие для модели регрессии выполнения условий на ошибки регрессии

Тогда OLS-оценка параметра считается BLUE оценкой, то есть среди линейных несмещенных оценок она имеет минимальную дисперсию, называемую эффективной оценкой.

Несмещенность в модели регрессии OLS-оценки коэффициента достаточно только при условии M = 0 на ошибку регрессии.

Далее рассмотрим статистические свойства оценки ^. Будем учитывать, что ошибки регрессии удовлетворяют условиям ошибки.

Обозначим через y^ = x^i предсказанные либо подогнанные (fitted) значения зависимой переменной. Тогда остатки регрессии определяются как

В парной модели регрессии без константы ∑ e не равна 0.

Обозначим RSS = ∑e∑ yy^ – это остаточная сумма квадратов в модели регрессии. Можно показать, что

Следовательно, статистика является несмещенной оценкой в дисперсии ошибок регрессии

Доверительный интервал с доверительной вероятностью ʏ имеет вид

P( ^ — s₁ * tкр 2 уже не имеет никакого смысла.

В качестве меры по «качеству подгонки» прямой, а также модели регрессии без константы может использоваться нецентрированный коэффициент R 2 , который определяется равенством

2 Влияние на коэффициенты регрессии масштаба измерения переменных

В реальной жизни социологи очень редко сталкивается с простыми моделями данных, линейными уравнениями с двумя переменными. Влияние каждого фактора может обычно объяснить только часть разброса по наблюдаемым значениям независимой переменной. При помощи метода частной корреляции можно проконтролировать эффекты от воздействий любых прочих контрольных переменных, которые можно измерить. Но еще более интересной задачей считается контроль за одновременным воздействием нескольких незави симых переменных на одну зависимую, также сравнение эффектов воздействий различных независимых переменных, предсказание влияния независимой переменной.

Уравнением множественной регрессии называется определенная модель в порождении данных. Очень важные допущения, которые принимаются в этой модели, касаются требования линейности, аддитивности в суммарном эффекте независимых переменных. Аддитивность означает, что воздействие разных независимых переменных суммируются, а не, к примеру, перемножаются (мультипликативный эффект, в отличии от аддитивного, имеет место лишь тогда, когда уровень воздействия одной независимой на зависимую переменную находится, в свою очередь, под влиянием иной независимой переменной, то есть между независимыми переменными происходит взаимодействие).

Регрессия происходит одновременно по двум и больше независимым переменным, и каждая из них вхожа в регрессионное уравнение по коэффициенту, позволяющему предсказать с минимальным количеством ошибок значения зависимой переменной (здесь критерием считается метод наименьших квадратов).

Коэффициент а может быть интерпретирован как показатель влияния каждой независимой на зависимую переменную при контроле в уравнении всех других независимых переменных. Коэффициенты регрессии обладают размерностью, показывая, на сколько единиц изменится зависимая при увеличении независимой переменной на одну единицу.

Регрессию также можно использовать и с целью предсказаний среднего группового значения, к примеру, среднего дохода по конкретной профессии. Как независимую переменную множественной регрессии можно использовать и дихотомические переменные, к которым приписываются значения 0, 1 (к примеру, пол).

При интерпретации результата регрессии стандартизованные коэффициенты, используют как показатели значимости и влияния соответствующих переменных. Данная трактовка верна только в определенных пределах. В случае нарушения некоторых условий сравнения абсолютных величин по стандартизованным коэффициентам может привести к неверным выводам. Это происходит потому, что коэффициенты регрессии очень подвержены влияниям случайных ошибок измерений. Использование ненадежного индикатора проводит сдвиг регрессионных коэффициентов к нулю. Другими словами, наиболее надежные индикаторы дают наиболее высокие оценки коэффициентов. Но нельзя также исключать и альтернативное объяснение, которое связывает более высокий коэффициент регрессии первой переменной с побочным эффектом методов измерений: их широта и пр.

Таким образом, для получений наиболее верного анализа данных в исследовании, масштаб измерений играет очень большую роль, так как при сильно отличающихся масштабах измерений результаты могут быть существенно различные.

Основы линейной регрессии

Что такое регрессия?

Разместим точки на двумерном графике рассеяния и скажем, что мы имеем линейное соотношение, если данные аппроксимируются прямой линией.

Если мы полагаем, что y зависит от x, причём изменения в y вызываются именно изменениями в x, мы можем определить линию регрессии (регрессия y на x), которая лучше всего описывает прямолинейное соотношение между этими двумя переменными.

Статистическое использование слова «регрессия» исходит из явления, известного как регрессия к среднему, приписываемого сэру Френсису Гальтону (1889).

Он показал, что, хотя высокие отцы имеют тенденцию иметь высоких сыновей, средний рост сыновей меньше, чем у их высоких отцов. Средний рост сыновей «регрессировал» и «двигался вспять» к среднему росту всех отцов в популяции. Таким образом, в среднем высокие отцы имеют более низких (но всё-таки высоких) сыновей, а низкие отцы имеют сыновей более высоких (но всё-таки довольно низких).

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

• a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).
• b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.
• a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Метод наименьших квадратов

Мы выполняем регрессионный анализ, используя выборку наблюдений, где a и b – выборочные оценки истинных (генеральных) параметров, α и β , которые определяют линию линейной регрессии в популяции (генеральной совокупности).

Наиболее простым методом определения коэффициентов a и b является метод наименьших квадратов (МНК).

Подгонка оценивается, рассматривая остатки (вертикальное расстояние каждой точки от линии, например, остаток = наблюдаемому y – предсказанный y, Рис. 2).

Линию лучшей подгонки выбирают так, чтобы сумма квадратов остатков была минимальной.

Рис. 2. Линия линейной регрессии с изображенными остатками (вертикальные пунктирные линии) для каждой точки.

Предположения линейной регрессии

Итак, для каждой наблюдаемой величины остаток равен разнице и соответствующего предсказанного Каждый остаток может быть положительным или отрицательным.

Можно использовать остатки для проверки следующих предположений, лежащих в основе линейной регрессии:

• Между и существует линейное соотношение: для любых пар данные должны аппроксимировать прямую линию. Если нанести на двумерный график остатки, то мы должны наблюдать случайное рассеяние точек, а не какую-либо систематическую картину.

• Остатки нормально распределены с нулевым средним значением;

• Остатки имеют одну и ту же вариабельность (постоянную дисперсию) для всех предсказанных величин Если нанести остатки против предсказанных величин от мы должны наблюдать случайное рассеяние точек. Если график рассеяния остатков увеличивается или уменьшается с увеличением то это допущение не выполняется;

Если допущения линейности, нормальности и/или постоянной дисперсии сомнительны, мы можем преобразовать или и рассчитать новую линию регрессии, для которой эти допущения удовлетворяются (например, использовать логарифмическое преобразование или др.).

Аномальные значения (выбросы) и точки влияния

«Влиятельное» наблюдение, если оно опущено, изменяет одну или больше оценок параметров модели (т.е. угловой коэффициент или свободный член).

Выброс (наблюдение, которое противоречит большинству значений в наборе данных) может быть «влиятельным» наблюдением и может хорошо обнаруживаться визуально, при осмотре двумерной диаграммы рассеяния или графика остатков.

И для выбросов, и для «влиятельных» наблюдений (точек) используют модели, как с их включением, так и без них, обращают внимание на изменение оценки (коэффициентов регрессии).

При проведении анализа не стоит отбрасывать выбросы или точки влияния автоматически, поскольку простое игнорирование может повлиять на полученные результаты. Всегда изучайте причины появления этих выбросов и анализируйте их.

Гипотеза линейной регрессии

При построении линейной регрессии проверяется нулевая гипотеза о том, что генеральный угловой коэффициент линии регрессии β равен нулю.

Если угловой коэффициент линии равен нулю, между и нет линейного соотношения: изменение не влияет на

Для тестирования нулевой гипотезы о том, что истинный угловой коэффициент равен нулю можно воспользоваться следующим алгоритмом:

Вычислить статистику критерия, равную отношению , которая подчиняется распределению с степенями свободы, где стандартная ошибка коэффициента

,

— оценка дисперсии остатков.

Обычно если достигнутый уровень значимости нулевая гипотеза отклоняется.

Можно рассчитать 95% доверительный интервал для генерального углового коэффициента :

где процентная точка распределения со степенями свободы что дает вероятность двустороннего критерия

Это тот интервал, который содержит генеральный угловой коэффициент с вероятностью 95%.

Для больших выборок, скажем, мы можем аппроксимировать значением 1,96 (то есть статистика критерия будет стремиться к нормальному распределению)

Оценка качества линейной регрессии: коэффициент детерминации R 2

Из-за линейного соотношения и мы ожидаем, что изменяется, по мере того как изменяется , и называем это вариацией, которая обусловлена или объясняется регрессией. Остаточная вариация должна быть как можно меньше.

Если это так, то большая часть вариации будет объясняться регрессией, а точки будут лежать близко к линии регрессии, т.е. линия хорошо соответствует данным.

Долю общей дисперсии , которая объясняется регрессией называют коэффициентом детерминации, обычно выражают через процентное соотношение и обозначают R 2 (в парной линейной регрессии это величина r 2 , квадрат коэффициента корреляции), позволяет субъективно оценить качество уравнения регрессии.

Разность представляет собой процент дисперсии который нельзя объяснить регрессией.

Нет формального теста для оценки мы вынуждены положиться на субъективное суждение, чтобы определить качество подгонки линии регрессии.

Применение линии регрессии для прогноза

Можно применять регрессионную линию для прогнозирования значения по значению в пределе наблюдаемого диапазона (никогда не экстраполируйте вне этих пределов).

Мы предсказываем среднюю величину для наблюдаемых, которые имеют определенное значение путем подстановки этого значения в уравнение линии регрессии.

Итак, если прогнозируем как Используем эту предсказанную величину и ее стандартную ошибку, чтобы оценить доверительный интервал для истинной средней величины в популяции.

Повторение этой процедуры для различных величин позволяет построить доверительные границы для этой линии. Это полоса или область, которая содержит истинную линию, например, с 95% доверительной вероятностью.

Подобным образом можно рассчитать более широкую область, внутри которой, как мы ожидаем, лежит наибольшее число (обычно 95%) наблюдений.

Простые регрессионные планы

Простые регрессионные планы содержат один непрерывный предиктор. Если существует 3 наблюдения со значениями предиктора P , например, 7, 4 и 9, а план включает эффект первого порядка P , то матрица плана X будет иметь вид

а регрессионное уравнение с использованием P для X1 выглядит как

Если простой регрессионный план содержит эффект высшего порядка для P , например квадратичный эффект, то значения в столбце X1 в матрице плана будут возведены во вторую степень:

а уравнение примет вид

Y = b 0 + b 1 P 2

Сигма -ограниченные и сверхпараметризованные методы кодирования не применяются по отношению к простым регрессионным планам и другим планам, содержащим только непрерывные предикторы (поскольку, просто не существует категориальных предикторов). Независимо от выбранного метода кодирования, значения непрерывных переменных увеличиваются в соответствующей степени и используются как значения для переменных X . При этом перекодировка не выполняется. Кроме того, при описании регрессионных планов можно опустить рассмотрение матрицы плана X , а работать только с регрессионным уравнением.

Пример: простой регрессионный анализ

Этот пример использует данные, представленные в таблице:

Рис. 3. Таблица исходных данных.

Данные составлены на основе сравнения переписей 1960 и 1970 в произвольно выбранных 30 округах. Названия округов представлены в виде имен наблюдений. Информация относительно каждой переменной представлена ниже:

Рис. 4. Таблица спецификаций переменных.

Задача исследования

Для этого примера будут анализироваться корреляция уровня бедности и степень, которая предсказывает процент семей, которые находятся за чертой бедности. Следовательно мы будем трактовать переменную 3 ( Pt_Poor ) как зависимую переменную.

Можно выдвинуть гипотезу: изменение численности населения и процент семей, которые находятся за чертой бедности, связаны между собой. Кажется разумным ожидать, что бедность ведет к оттоку населения, следовательно, здесь будет отрицательная корреляция между процентом людей за чертой бедности и изменением численности населения. Следовательно мы будем трактовать переменную 1 ( Pop_Chng ) как переменную-предиктор.

Просмотр результатов

Коэффициенты регрессии

Рис. 5. Коэффициенты регрессии Pt_Poor на Pop_Chng.

На пересечении строки Pop_Chng и столбца Парам. не стандартизованный коэффициент для регрессии Pt_Poor на Pop_Chng равен -0.40374 . Это означает, что для каждого уменьшения численности населения на единицу, имеется увеличение уровня бедности на .40374. Верхний и нижний (по умолчанию) 95% доверительные пределы для этого не стандартизованного коэффициента не включают ноль, так что коэффициент регрессии значим на уровне p . Обратите внимание на не стандартизованный коэффициент, который также является коэффициентом корреляции Пирсона для простых регрессионных планов, равен -.65, который означает, что для каждого уменьшения стандартного отклонения численности населения происходит увеличение стандартного отклонения уровня бедности на .65.

Распределение переменных

Коэффициенты корреляции могут стать существенно завышены или занижены, если в данных присутствуют большие выбросы. Изучим распределение зависимой переменной Pt_Poor по округам. Для этого построим гистограмму переменной Pt_Poor .

Рис. 6. Гистограмма переменной Pt_Poor.

Как вы можете заметить, распределение этой переменной заметно отличается от нормального распределения. Тем не менее, хотя даже два округа (два правых столбца) имеют высокий процент семей, которые находятся за чертой бедности, чем ожидалось в случае нормального распределения, кажется, что они находятся «внутри диапазона.»

Рис. 7. Гистограмма переменной Pt_Poor.

Это суждение в некоторой степени субъективно. Эмпирическое правило гласит, что выбросы необходимо учитывать, если наблюдение (или наблюдения) не попадают в интервал (среднее ± 3 умноженное на стандартное отклонение). В этом случае стоит повторить анализ с выбросами и без, чтобы убедиться, что они не оказывают серьезного эффекта на корреляцию между членами совокупности.

Диаграмма рассеяния

Если одна из гипотез априори о взаимосвязи между заданными переменными, то ее полезно проверить на графике соответствующей диаграммы рассеяния.

Рис. 8. Диаграмма рассеяния.

Диаграмма рассеяния показывает явную отрицательную корреляцию ( -.65 ) между двумя переменными. На ней также показан 95% доверительный интервал для линии регрессии, т.е., с 95% вероятностью линия регрессии проходит между двумя пунктирными кривыми.

Критерии значимости

Рис. 9. Таблица, содержащая критерии значимости.

Критерий для коэффициента регрессии Pop_Chng подтверждает, что Pop_Chng сильно связано с Pt_Poor , p .

На этом примере было показано, как проанализировать простой регрессионный план. Была также представлена интерпретация не стандартизованных и стандартизованных коэффициентов регрессии. Обсуждена важность изучения распределения откликов зависимой переменной, продемонстрирована техника определения направления и силы взаимосвязи между предиктором и зависимой переменной.

Опции программы MS EXCEL, предназначенные для регрессионного анализа

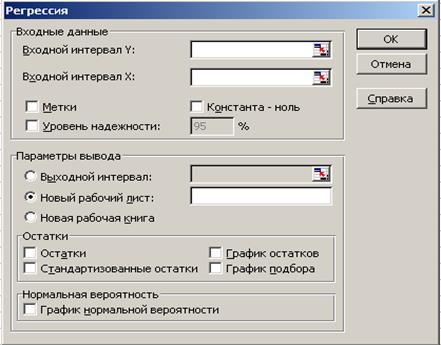
3.4.3.1 Использование инструмента анализа «Регрессия»

В пакете «Анализ данных» инструмент «Регрессия» (рис. 4.3) предлагает ли­нейный регрессионный анализ, который заключается в подборе графика для набора наблюдений с помощью метода наименьших квадратов. Регрессия используется для анализа воздействия на отдельную зависимую переменную значений одной или более (до 16) независимых переменных. То есть во «Входной интервал X» (рис. 4.3) можно вводить до 16 диапазонов. (Диапазоны обязательно должны быть представлены в столбцах.)Во«Входной интервал Y» вводят один диапазон, состоящий из одного столбца.

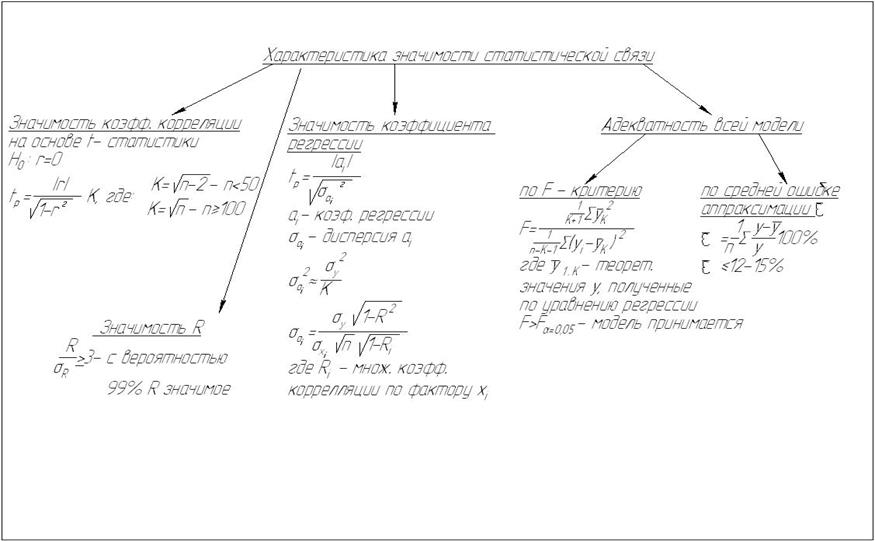
Рис. 4.2. Характеристики достоверности статистической связи

Рис. 4.3. Диалоговое окно инструмента анализа «Регрессия»

При желании получения уравнения регрессии без свободного члена (чтобы линия регрессии прошла через начало координат) следует в опцию «Константа — ноль» поставить «галочку». «Галочки» в опции «Остатки», «График остатков», «График подбора» или «Стандартизированные остатки» устанавливаются при необходимости исследования несоответствий между экспериментальными и теоретическими значениями Y, определяемыми уравнением регрессии. «Остаток» представляет собой разницу между фактическим и теоретическим значениями Y. «Стандартизированный остаток» представляет собой отношение «остатка» к «стандартной ошибке единичного наблюдения регрессионной статистики» (см. ниже). «График остатков» располагается в координатах x — величина остатка. По нему наглядно видны значения «остатка» для разных аргументов, что позволяет обнаружить «выбросы» — самые большие отклонения от теоретической модели, которые могут свидетельствовать о каком-то сбое, ошибке в получении результата. Процедура устранения таких «выбросов» называется «цензурированием».

На «графике подбора» в координатах x — Y показываются фактические и «предсказанные» данной регрессионной моделью значения Y.

Опция «График нормальной вероятности» позволяет в соответствии с появляющейся таблицей «ВЫВОД ВЕРОЯТНОСТИ» построить диаграмму в координатах «Персентиль выборки» — Y. То есть полученные значения Y в данном случае представлены в виде ранжированного вариационного ряда.

Результаты регрессионного анализа представляются как минимум (если не включены дополнительно отмеченные выше опции) в виде трёх таблиц.

1. Таблица «Регрессионная статистика» включает в себя рассчитанные значения следующих показателей:

— множественного коэффициента корреляции («Множественный R»);

— квадрата множественного коэффициента корреляции (коэффициента детерминации, «R-квадрат»);

— числа наблюдений n (число факторов обозначается k, см. ниже);

— нормированного коэффициента детерминации, объективно определяющего достоверность связи, так как, в отличие от обычного коэффициента детерминации, он не зависит от числа опытов (n) и числа факторов (k):

(4.1)

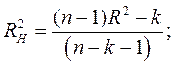
— стандартной ошибки единичного наблюдения:

(4.2)

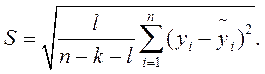
2. Таблица «Дисперсионный анализ» включает в себя обусловленные регрессией («Регрессия»), необусловленные регрессией («Остаток») и суммарные:

— число степеней свободы df;

— сумму квадратов разностей (дисперсии SS);

— оценки дисперсий, приходящихся на одну степень свободы (MS).

Кроме того, выводятся расчётное значение F-критерия Фишера ( 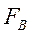) и «значимость F». Таким образом, в отличие от полного дисперсионного анализа (см. главу 4), табличное «критическое» значение F-критерия Фишера в данном случае не представлено. Поэтому вывод о существенности влияния рассматриваемых факторов в данном случае можно делать из сравнения величины «значимости F» с принятым уровнем доверительной вероятности α. При «значимость F»

3. Таблица результатов собственно регрессионного анализа(информация об уравнении регрессии) включает в себя:

— значение свободного члена уравнения 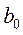(Y-пересечение);

— коэффициенты регрессии 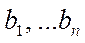для каждого фактора;

— «Стандартную ошибку» коэффициентов регрессии ;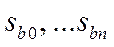

—«t-статистику» — расчётные значения коэффициентов Стьюдента для соответствующих коэффициентов регрессии ;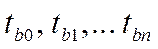

— «P-Значение» — вероятность значимости для соответствующих коэффициентов регрессии;

— нижние и верхние интервальные оценки (отклонения) для коэффициентов регрессии с 95-процентной и любой другой (заданной) доверительной вероятностью.

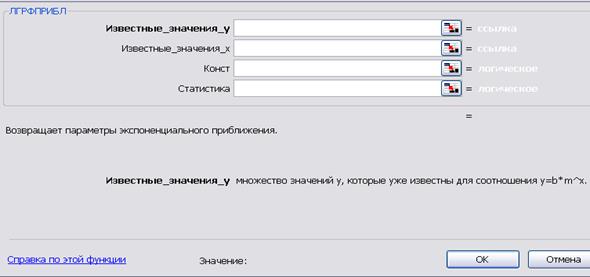
Поскольку «критические» (табличные) значения коэффициентов Стьюдента в этой таблице не приводятся, о достоверности рассчитанных коэффициентов регрессии можно судить по величине «P-Значения» в сравнении с принятым уровнем доверительной вероятности α. При «P-Значение» x 1 ) ×…×(m_n x n ), (4.5)

где значения m являются основанием, возводимым в степень x, а значения b постоянны.

Рис. 4.8. Аргументы функции ЛГРФПРИБЛ

«Конст» (рис. 4.8) — логическое значение, как и в функциях, описывающих линейную регрессию. Но в данном случае оно указывает, требуется ли, чтобы константа b была равна 1 (единице). Если «Конст» имеет значение ИСТИНА или отсутствует, то b вычисляется обычным образом. Если «Конст» имеет значение ЛОЖЬ, то значения m подбираются так, чтобы выполнялось b = 1.

При выведении полной статистики (опция «Статистика») её структура полностью соответствует структуре, выводимой в этом случае функцией ЛИНЕЙН, и включает коэффициенты регрессии, их стандартные отклонения, число степеней свободы, коэффициент детерминации и суммы квадратов остатков.

Функция РОСТ (рис. 4.9) также применяется для аппроксимации связи x- и y-значений экспоненциальной кривой, но по сравнению с функцией ЛГРФПРИБЛ решает более скромные задачи — рассчитывает значения y для новых значений x, не касаясь рассеяния и статистики.