Уравнение регрессии: Что это такое и как его использовать
Уравнение регрессии: Обзор
Уравнение регрессии используется в статистике для того, чтобы выяснить, какая связь, если таковая существует, существует между наборами данных. Например, если каждый год измерять рост ребенка, то можно обнаружить, что он растет примерно на 3 дюйма в год. Эта тенденция (которая растет на 3 дюйма в год) может быть смоделирована с помощью уравнения регрессии. Фактически, большинство вещей в реальном мире (от цен на газ до ураганов) можно смоделировать с помощью некоего уравнения, что позволяет нам предсказывать будущие события.
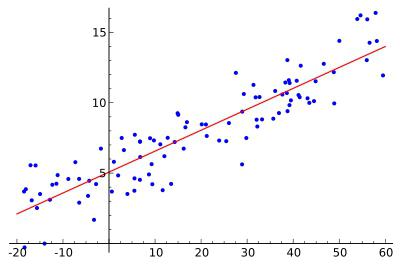
Линия регрессии – это “самая подходящая” линия для ваших данных. По сути, вы рисуете линию, которая наилучшим образом представляет точки данных. Она представляет собой среднее арифметическое того, где выравниваются все точки. В линейной регрессии линия регрессии является абсолютно прямой линией:
Линия регрессии представлена уравнением. В данном случае уравнение равно -2.2923x + 4624.4. Это означает, что если бы вы строили график уравнения -2.2923x + 4624.4, то линия была бы грубой аппроксимацией для ваших данных.
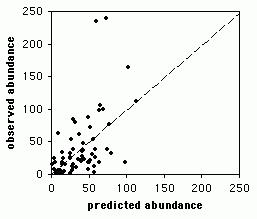
Не очень распространено, чтобы все точки данных действительно попадали на линию регрессии. На рисунке выше точки немного рассеяны вокруг линии. На следующем изображении точки падают на линию. Изогнутая форма этой линии является результатом полиномиальной регрессии, которая укладывает точки в уравнение полинома.
Уравнение регрессии: Что это такое и как его использовать
Статистические определения > Что такое уравнение регрессии?
Уравнение регрессии: Обзор
Уравнение регрессии используется в статистике для того, чтобы выяснить, какая связь, если таковая существует, существует между наборами данных. Например, если каждый год измерять рост ребенка, то можно обнаружить, что он растет примерно на 3 дюйма в год. Эта тенденция (которая растет на 3 дюйма в год) может быть смоделирована с помощью уравнения регрессии. Фактически, большинство вещей в реальном мире (от цен на газ до ураганов) можно смоделировать с помощью некоего уравнения, что позволяет нам предсказывать будущие события.
Линия регрессии – это “самая подходящая” линия для ваших данных. По сути, вы рисуете линию, которая наилучшим образом представляет точки данных. Она представляет собой среднее арифметическое того, где выравниваются все точки. В линейной регрессии линия регрессии является абсолютно прямой линией:
Линия линейной регрессии.
Линия регрессии представлена уравнением. В данном случае уравнение равно -2.2923x + 4624.4. Это означает, что если построить график уравнения -2.2923x + 4624.4, то линия будет представлять собой грубую аппроксимацию для Ваших данных.
Не очень распространено, чтобы все точки данных действительно попадали на линию регрессии. На рисунке выше точки немного рассеяны вокруг линии. На следующем изображении точки падают на линию. Изогнутая форма этой линии является результатом полиномиальной регрессии, которая укладывает точки в уравнение полинома.
В результате полиномиальной регрессии получается кривая линия.
Результатом полиномиальной регрессии является кривая линия.
Регрессия и линии прогнозирования
Регрессия полезна, так как позволяет делать прогнозы о данных. Первый график выше – с 1995 по 2015 год. Если вы хотите предсказать, что произойдет в 2020 году, вы можете поместить его в уравнение:
Отрицательное выпадение осадков не имеет особого смысла, но можно сказать, что до 2020 года осадки выпадут на 0 дюймов. Согласно этой конкретной линии регрессии, рано или поздно это произойдет в 2018 году:
Для чего нужно уравнение регрессии?
Уравнения регрессии могут помочь вам понять, подходят ли ваши данные для уравнения. Это чрезвычайно полезно, если вы хотите сделать прогноз на основе своих данных – как будущих прогнозов, так и указаний на прошлое поведение. Например, вы можете захотеть узнать, сколько ваших сбережений будет стоить в будущем. Или, возможно, вы захотите предсказать, сколько времени понадобится на выздоровление от болезни.
Существуют различные типы уравнений регрессии. К наиболее распространенным относятся экспоненциальная линейная регрессия и простая линейная регрессия (для адаптации данных к экспоненциальному уравнению или линейному уравнению). В элементарной статистике уравнение регрессии, с которым вы, скорее всего, столкнетесь, является линейной формой.
Расчет линейной регрессии
Есть несколько способов найти линию регрессии, даже вручную и с помощью технологий, таких как Excel (см. ниже). Поиск линии регрессии очень скучен вручную. Следующее видео иллюстрирует шаги:
Линию регрессии также можно найти в калькуляторах TI:
TI 83 Регрессия.
Как выполнять регрессию TI-89.
Уравнение линейной регрессии показано ниже.
Для того, чтобы данные вписались в уравнение, необходимо сначала понять, какая общая схема подходит для данных. Общие шаги для выполнения регрессии включают в себя составление дисперсионной диаграммы, а затем гипотезу о том, какой тип уравнения может быть наиболее подходящим. Затем можно выбрать наилучшее уравнение регрессии для задания.
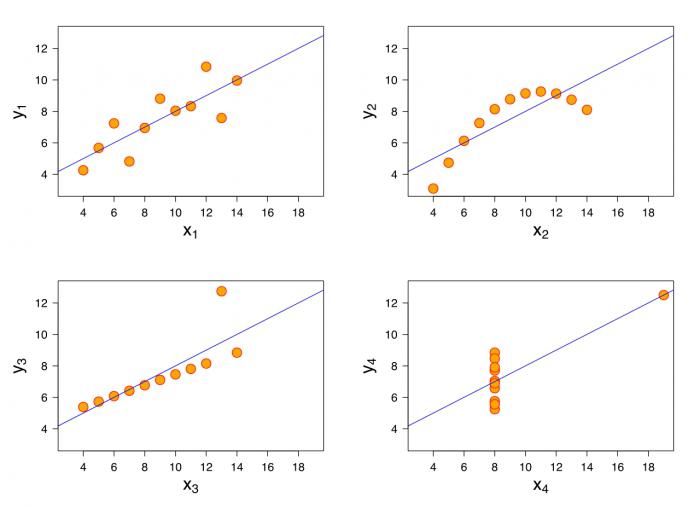
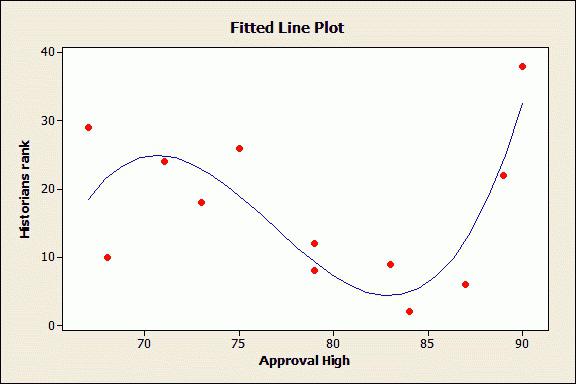
Однако, как видно на следующем рисунке, не всегда легко выбрать подходящее уравнение регрессии, особенно при работе с реальными данными. Иногда получаются “шумные” данные, которые, кажется, не подходят ни под одно уравнение. Если большинство данных, кажется, следуют шаблону, вы можете пропустить пропуски. На самом деле, если игнорировать промахи, данные, кажется, моделируются экспоненциальным уравнением.
Уравнение регрессии используется для построения
При наличии корреляционной связи между факторными и результативными признаками врачам нередко приходится устанавливать, на какую величину может измениться значение одного признака при изменении другого на общепринятую или установленную самим исследователем единицу измерения.
Например, как изменится масса тела школьников 1-го класса (девочек или мальчиков), если рост их увеличится на 1 см. В этих целях применяется метод регрессионного анализа.
Наиболее часто метод регрессионного анализа применяется для разработки нормативных шкал и стандартов физического развития.
- Определение регрессии. Регрессия — функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым.
С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период.
Определение коэффициента регрессии. Коэффициент регрессии — абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого связанного с ним признака на установленную единицу измерения.
Формула коэффициента регрессии. Rу/х = rху x (σу / σx)
где Rу/х — коэффициент регрессии;
rху — коэффициент корреляции между признаками х и у;
(σу и σx) — среднеквадратические отклонения признаков x и у.
В нашем примере [rху = — 0,96 коэффициент корреляции между изменениями среднемесячной температуры в осенне-зимний период (х) и средним числом инфекционно-простудных заболеваний (у)];
σх = 4,6 (среднеквадратическое отклонение температуры воздуха в осенне-зимний период;
σу = 8,65 (среднеквадратическое отклонение числа инфекционно-простудных заболеваний).
Таким образом, Rу/х — коэффициент регрессии.
Rу/х = -0,96 х (4,6 / 8,65) = 1,8, т.е. при снижении среднемесячной температуры воздуха (x) на 1 градус среднее число инфекционно-простудных заболеваний (у) в осенне-зимний период будет изменяться на 1,8 случаев.
Уравнение регрессии. у = Му + Ry/x (х — Мx)
где у — средняя величина признака, которую следует определять при изменении средней величины другого признака (х);
х — известная средняя величина другого признака;
Ry/x — коэффициент регрессии;
Мх, Му — известные средние величины признаков x и у.
Например, среднее число инфекционно-простудных заболеваний (у) можно определить без специальных измерений при любом среднем значении среднемесячной температуры воздуха (х). Так, если х = — 9°, Rу/х = 1,8 заболеваний, Мх = -7°, Му = 20 заболеваний, то у = 20 + 1,8 х (9-7) = 20 + 3,6 = 23,6 заболеваний.
Данное уравнение применяется в случае прямолинейной связи между двумя признаками (х и у).
Назначение уравнения регрессии. Уравнение регрессии используется для построения линии регрессии. Последняя позволяет без специальных измерений определить любую среднюю величину (у) одного признака, если меняется величина (х) другого признака. По этим данным строится график — линия регрессии, по которой можно определить среднее число простудных заболеваний при любом значении среднемесячной температуры в пределах между расчетными значениями числа простудных заболеваний.
Сигма регрессии (формула).
где σRу/х — сигма (среднеквадратическое отклонение) регрессии;
σу— среднеквадратическое отклонение признака у;
rху — коэффициент корреляции между признаками х и у.
Так, если σу — среднеквадратическое отклонение числа простудных заболеваний = 8,65; rху — коэффициент корреляции между числом простудных заболеваний (у) и среднемесячной температурой воздуха в осенне-зимний период (х) равен — 0,96, то
Назначение сигмы регрессии. Дает характеристику меры разнообразия результативного признака (у).
Например, характеризует разнообразие числа простудных заболеваний при определенном значении среднемесячной температуры воздуха в осеннне-зимний период. Так, среднее число простудных заболеваний при температуре воздуха х1 = -6° может колебаться в пределах от 15,78 заболеваний до 20,62 заболеваний.
При х2 = -9° среднее число простудных заболеваний может колебаться в пределах от 21,18 заболеваний до 26,02 заболеваний и т.д.
Сигма регрессии используется при построении шкалы регрессии, которая отражает отклонение величин результативного признака от среднего его значения, отложенного на линии регрессии.
- коэффициент регрессии — Rу/х;
- уравнение регрессии — у = Му + Rу/х (х-Мx);
- сигма регрессии — σRx/y
- определить коэффициент регрессии по формуле (см. п. 3). Например, следует определить, насколько в среднем будет меняться масса тела (в определенном возрасте в зависимости от пола), если средний рост изменится на 1 см.
- по формуле уравнения регрессии (см п. 4) определить, какой будет в среднем, например, масса тела (у, у2, у3. )* для определеного значения роста (х, х2, х3. ).
________________
* Величину «у» следует рассчитывать не менее чем для трех известных значений «х».
При этом средние значения массы тела и роста (Мх, и Му) для определенного возраста и пола известны
Для графического изображения шкалы регрессии на графике сначала отмечаются значения х, х2, х3 (ось ординат), т.е. строится линия регрессии, например зависимости массы тела (у) от роста (х).
Затем в соответствующих точках у1, y2, y3 отмечаются числовые значения сигмы регрессии, т.е. на графике находят наименьшее и наибольшее значения у1, y2, y3.
Практическое использование шкалы регрессии. Разрабатываются нормативные шкалы и стандарты, в частности по физическому развитию. По стандартной шкале можно дать индивидуальную оценку развития детей. При этом физическое развитие оценивается как гармоничное, если, например, при определенном росте масса тела ребенка находится в пределах одной сигмы регрессии к средней расчетной единице массы тела — (у) для данного роста (x) (у ± 1 σRy/x).
Физическое развитие считается дисгармоничным по массе тела, если масса тела ребенка для определенного роста находится в пределах второй сигмы регрессии: (у ± 2 σRy/x)
Физическое развитие будет резко дисгармоничным как за счет избыточной, так и за счет недостаточной массы тела, если масса тела для определенного роста находится в пределах третьей сигмы регрессии (у ± 3 σRy/x).
По результатам статистического исследования физического развития мальчиков 5 лет известно, что их средний рост (х) равен 109 см, а средняя масса тела (у) равна 19 кг. Коэффициент корреляции между ростом и массой тела составляет +0,9, средние квадратические отклонения представлены в таблице.
Требуется:
- рассчитать коэффициент регрессии;
- по уравнению регрессии определить, какой будет ожидаемая масса тела мальчиков 5 лет при росте, равном х1 = 100 см, х2 = 110 см, х3= 120 см;
- рассчитать сигму регрессии, построить шкалу регрессии, результаты ее решения представить графически;
- сделать соответствующие выводы.
Условие задачи и результаты ее решения представлены в сводной таблице.
| Условия задачи | Pезультаты решения задачи | ||||||||
| уравнение регрессии | сигма регрессии | шкала регрессии (ожидаемая масса тела (в кг)) | |||||||
| М | σ | rху | Rу/x | х | У | σ Rx/y | y — σRу/х | y + σRу/х | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| Рост (х) | 109 см | ± 4,4см | +0,9 | 0,16 | 100см | 17,56 кг | ± 0,35 кг | 17,21 кг | 17,91 кг |
| Масса тела (y) | 19 кг | ± 0,8 кг | 110 см | 19,16 кг | 18,81 кг | 19,51 кг | |||
| 120 см | 20,76 кг | 20,41 кг | 21,11 кг | ||||||
Решение.
- Коэффициент регрессии:
Rу/х = rху х (σу / σх) = +0,9 х (0,8 / 4,4) = 0,16 кг/см.
Таким образом, при увеличении роста мальчиков 5 лет на 1 см масса тела увеличивается на 0,16 кг.
| х1 = 100 см | у1 = 19 + 0,16 (100-109) = 17,56 кг |
| х2 = 110 см | у2 = 19 + 0,16 (110-109) = 19,16 кг |
| х3 = 120 см | У3 = 19 + 0,16 (120-109) = 20, 76 кг |
| Рост и его значения | Среднее значение массы тела | Наименьшее значение массы тела | Наибольшее значение массы тела |
| х | У | У — σRy/x | У — σRy/x |
| 100 см (1) | 17,56 кг | 17,21 кг | 17,91 кг |
| 110 см (2) | 19,16 кг | 18,81 кг | 19,51 кг |
| 120 см (3) | 20,76 кг | 20,41 кг | 21,11 кг |
Графическое изображение регрессии. Шкала регрессии массы тела по росту 5-летних мальчиков
Вывод. Таким образом, шкала регрессии в пределах расчетных величин массы тела позволяет определить ее при любом другом значении роста или оценить индивидуальное развитие ребенка. Для этого следует восстановить перпендикуляр к линии регрессии.
Применение методов статистического анализа для изучения общественного здоровья и здравоохранения. Под ред. чл.-корр. РАМН, проф. В.З.Кучеренко. М., «Гэотар-Медиа», 2007, учебное пособие для вузов
- Власов В.В. Эпидемиология. — М.: ГЭОТАР-МЕД, 2004. — 464 с.
- Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. — М.: ГЭОТАР-МЕД, 2007. — 512 с.
- Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. — М.: Медицина, 2003. — 368 с.
- Миняев В.А., Вишняков Н.И. и др. Социальная медицина и организация здравоохранения (Руководство в 2 томах). — СПб, 1998. -528 с.
- Кучеренко В.З., Агарков Н.М. и др.Социальная гигиена и организация здравоохранения (Учебное пособие) — Москва, 2000. — 432 с.
- С. Гланц. Медико-биологическая статистика. Пер с англ. — М., Практика, 1998. — 459 с.
Уравнение регрессии. Уравнение множественной регрессии
Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.
Определение понятия регрессии
В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).
Какие бывают типы связей между переменными
В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.
Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.
Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.
Виды регрессий
На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.
Гиперболическая, линейная и логарифмическая
Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.
Множественная и нелинейная
Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х1 , х2 . хс)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.
Обратные и парные виды регрессий
Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.
Понятие корреляции
Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.
Методы
Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.
Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.
В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.
Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).
Корреляция для множественной регрессии
Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.
Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.
Метод наименьших квадратов
Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.
Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.
Параметры уравнений
Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.
Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.
Сгруппированные данные
Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.
Множественное парное уравнение регрессии: оценка важности связи
Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x1,x2,…,xm)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.
Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.
Линейная функция изображается в форме такой взаимосвязи: у = а0 + a1х1 + а2х2,+ . + amxm. При этом а2, am, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.
Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах1 b1 х2 b2 . xm bm . В данном случае показатели b1, b2. bm – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.
Какие факторы необходимо учитывать при построении множественной регрессии
Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.
Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:
- Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
- Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
- В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.
Методы построения
Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:
- Способ исключения.
- Способ включения.
- Пошаговый анализ регрессии.
Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.
Методы многомерного анализа
Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.
http://bono-esse.ru/blizzard/Medstat/Statan/stat_ra.html
http://www.syl.ru/article/178055/new_uravnenie-regressii-uravnenie-mnojestvennoy-regressii