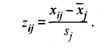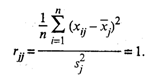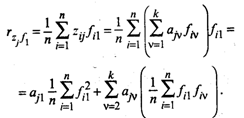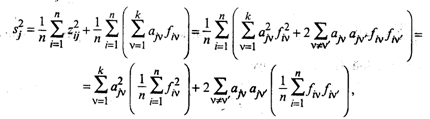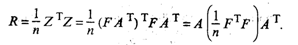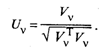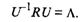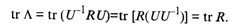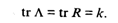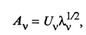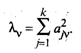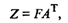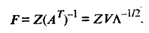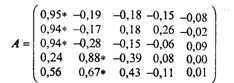Уравнение регрессии на главных компонентах

53.3. Компонентный анализ

Компонентный анализ предназначен для преобразования системы k исходных признаков в систему k новых показателей (главных компонент). Главные компоненты не коррелированы между собой и упорядочены по величине их дисперсий, причем первая главная компонента имеет наибольшую дисперсию, а последняя, k-я — наименьшую. При этом выявляются неявные, непосредственно не измеряемые, но объективно существующие закономерности, обусловленные действием как внутренних, так и внешних причин.

Компонентный анализ является одним из основных методов факторного анализа. В задачах снижения размерности и классификации обычно используются т первых компонент (т

размерности п х k, где х_ij.— значение j -го показателя у i -го наблюдения ( i = 1, 2, . n ; j = 1, 2, . k), вычисляют средние значения показателей 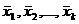а также s ₁, . s_k и матрицу нормированных значений

Рассчитывается матрица парных коэффициентов корреляции:

(53.24)

(53.25)

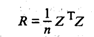
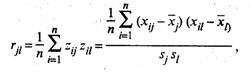
На главной диагонали матрицы R , т.е. при j = l , расположены элементы

Модель компонентного анализа имеет вид

(53.26)

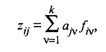
где a_iv — «вес», т.е. факторная нагрузка v-й главной компоненты на j -ю переменную;

f _iv — значение v-й главной компоненты для i -го наблюдения (объекта), где v = 1, 2, . k .

В матричной форме модель (53.26) имеет вид

(53.27)

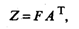
f _iv — значение v-й главной компоненты для i -го наблюдения (объекта);

a_iv — значение факторной нагрузки v-й главной компоненты на j -ю переменную.

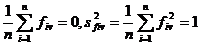
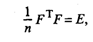
Матрица F описывает п наблюдений в пространстве k главных компонент. При этом элементы матрицы F нормированы, т.е. f_v = , a главные компоненты не коррелированы между собой. Из этого следует, что

(53.28)

Выражение (53.28) может быть представлено в виде

(53.29)

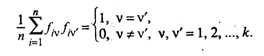
С целью интерпретации элементов матрицы А рассмотрим выражение для парного коэффициента корреляции между переменной z_j и, например, f ₁-й главной компонентой. Так как z _о и f ₁ нормированы, будем иметь с учетом (53.26):

Принимая во внимание (53.29), окончательно получим

Рассуждая аналогично, можно записать в общем виде

(53.30)

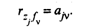
для всех j = 1, 2, . k и v = 1, 2, . k.

Таким образом, элемент a_jv матрицы факторных нагрузок А характеризует тесноту линейной связи между исходной переменной z_j и главной компонентой f_v , т.е. –1 ≤ a_jv ≤ +1.

Рассмотрим теперь выражение для дисперсии нормированной переменной z_j . С учетом (53.26) будем иметь

Учитывая (53.29), окончательно получим

(53.31)

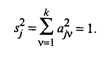
По условию, переменные z_j нормированы и s 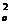= 1. Таким образом, дисперсия переменной z_j, согласно (53.31), представлена своими составляющими, определяющими долю вклада в нее всех k главных компонент.

Полный вклад v-й главной компоненты в дисперсию всех k исходных признаков вычисляется по формуле

(53.32)

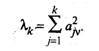
Одно из основополагающих условий метода главных компонент связано с представлением корреляционной матрицы R через матрицу факторных нагрузок А. Подставив для этого (53.27) в (53.24), будем иметь

Учитывая (53.28), окончательно получим

(53.33)

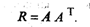
Перейдем теперь непосредственно к отысканию собственных значений и собственных векторов корреляционной матрицы R.

Из линейной алгебры известно, что для любой симметричной матрицы R всегда существует такая ортогональная матрица U , что выполняется условие

(53.34)

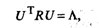
Так как матрица R положительно определена, т.е. ее главные миноры положительны, то все собственные значения λ _v > 0 для любых v =1, 2, . k .

В компонентном анализе элементы матрицы Λ ранжированы: λ₁ ≥ λ₂ ≥ . ≥ λ _v . ≥ λ _k ≥ 0. Как будет показано ниже, собственное значение λ _v характеризует вклад v-й главной компоненты в суммарную дисперсию исходного признакового пространства.

Таким образом, первая главная компонента вносит наибольший вклад в суммарную дисперсию, а последняя, k-я, — наименьший.

В ортогональной матрице U собственных векторов v-й столбец является собственным вектором, соответствующим λ _v -му значению.

Собственные значения λ₁ ≥ . ≥ λ _v . ≥ λ _k находятся как корни характеристического уравнения

(53.35)

Собственный вектор V_v, соответствующий собственному значению λ _v корреляционной матрицы R, определяется как отличное от нуля решение уравнения, которое следует из (53.34):

(53.36)

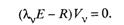
Нормированный собственный вектор U_v равен

Из условия ортогональности матрицы U следует, что U -1 = U T , но тогда, по определению, матрицы R и Λ подобны, так как они, согласно (53.34), удовлетворяют условию

Так как у подобных матриц суммы диагональных элементов равны, то

Учитывая, что сумма диагональных элементов матрицы R равна k , будем иметь

(53.37)

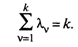
Представим матрицу факторных нагрузок А в виде

(53.38)

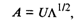
а v-й столбец матрицы А — как

где U_v — собственный вектор матрицы R, соответствующий собственному значению λ _v .

Найдем норму вектора А_v:

(53.39)

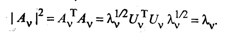
Здесь учитывалось, что вектор U_v — нормированный и U 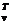U_v = 1. Таким образом,

Сравнив полученный результат с (53.32), можно сделать вывод, что собственное значение λ _v характеризует вклад v-й главной компоненты в суммарную дисперсию всех исходных признаков. Из (53.38) следует, что

(53.40)

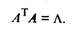
Согласно (53.37), общий вклад всех главных компонент в суммарную дисперсию равен k . Тогда удельный вклад v-й главной компоненты определяется по формуле .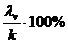

Суммарный вклад т первых главных компонент определяется из выражения .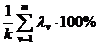

Обычно для анализа используют т первых главных компонент, вклад которых в суммарную дисперсию превышает 60—70%.

Матрица факторных нагрузок А используется для экономической интерпретации главных компонент, которые представляют собой линейные функции исходных признаков. Для экономической интерпретации f _v используются лишь те х_j, для которых | a_jv | > 0,5.

Значения главных компонент для каждого i -го объекта ( i = 1, 2, . n ) задаются матрицей F .

Матрицу значений главных компонент можно получить из формулы

Уравнение регрессии на главных компонентах строится по алгоритму пошагового регрессионного анализа, где в качестве аргументов используются главные компоненты, а не исходные показатели. К достоинству последней модели следует отнести тот факт, что главные компоненты не коррелированы. При построении уравнений регрессии следует учитывать все главные компоненты.

Пример. Построение регрессионного уравнения

По данным примера из § 53.2 провести компонентный анализ и построить уравнение регрессии урожайности Y на главных компонентах.

Решение. В примере из § 53.2 пошаговая процедура регрессионного анализа позволила исключить отрицательное значение мультиколлинеарности на качество регрессионной модели за счет значительной потери информации. Из пяти исходных показателей в окончательную модель вошли только два ( x ₁ и x₄). Более рациональным в условиях мультиколлинеарности можно считать построение уравнения регрессии на главных компонентах, которые являются линейными функциями всех исходных показателей и не коррелированы между собой.

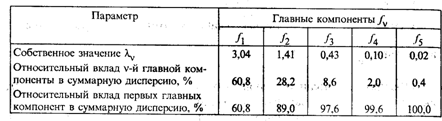
Воспользовавшись методом главных компонент, найдем собственные значения и на их основе — вклад главных компонент в суммарную дисперсию исходных показателей x ₁ , х₂, х₃, х₄, х₅ (табл. 53.2).

Собственные значения главных компонент

Ограничимся экономической интерпретацией двух первых главных компонент, общий вклад которых в суммарную дисперсию составляет 89,0%. В матрице факторных нагрузок

звездочкой указаны элементы а_jv = rx_jf_v , учитывающиеся при интерпретации главных компонент f_v , где j , v = 1, 2, . 5.

Из матрицы факторных нагрузок А следует, что первая главная компонента наиболее тесно связана со следующими показателями: x ₁ — число колесных тракторов на 100 га ( a ₁₁ = rx ₁ f ₁ = 0,95); х₂ — число зерноуборочных комбайнов на 100 га ( rx ₂ f ₁ = 0,97); х₃ — число орудий поверхностной обработки почвы на 100 га ( rx ₃ f ₁ = 0,94). В этой связи первая главная компонента — f ₁ — интерпретирована как уровень механизации работ.

Вторая главная компонента — f ₂ — тесно связана с количеством удобрений (х₄) и химических средств оздоровления растений ( x ₅ ), расходуемых на гектар, и интерпретирована как уровень химизации растениеводства.

Уравнение регрессии на главных компонентах строится по данным вектора значений результативного признака Y и матрицы F значений главных компонент.

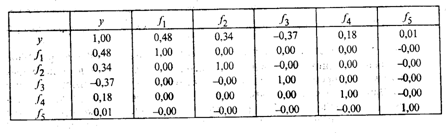
Некоррелированность главных компонент между собой и тесноту их связи с результативным признаком у показывает матрица парных коэффициентов корреляции (табл. 53.3).

Анализ матрицы парных коэффициентов корреляции свидетельствует о том, что результативный признак у наиболее тесно связан с первой (r_yf1 = 0,48), третьей ( r_{yf 3} = 0,37) и. второй (r_yf2 = 0,34) главными компонентами. Можно предположить, что только эти главные компоненты войдут в регрессионную модель у.

Матрица парных коэффициентов корреляции

Первоначально в модель у включают все главные компоненты (в скобках указаны расчетные значения t -критерия):

(53.41)

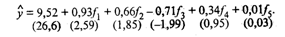
Качество модели характеризуют: множественный коэффициент детерминации r = 0,517, средняя относительная ошибка аппроксимации = 10,4%, остаточная дисперсия s 2 = 1,79 и F _набл = 121. Ввиду того что F _набл > F_кр =2,85 при α = 0,05, v₁ = 6, v ₂ = 14, уравнение регрессии значимо и хотя бы один из коэффициентов регрессии — β₁, β₂, β₃, β₄ — не равен нулю.

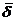
Если значимость уравнения регрессии (гипотеза Н₀: β₁ = β₂ = β₃ = β₄ = 0 проверялась при α = 0,05, то значимость коэффициентов регрессии, т.е. гипотезы H ₀ : β _j = 0 (j = 1, 2, 3, 4), следует проверять при уровне значимости, большем, чем 0,05, например при α = 0,1. Тогда при α = 0,1, v = 14 величина t _кр = 1,76, и значимыми, как следует из уравнения (53.41), являются коэффициенты регрессии β₁, β₂, β₃.

Учитывая, что главные компоненты не коррелированы между собой, можно сразу исключить из уравнения все незначимые коэффициенты, и уравнение примет вид

(53.42)

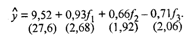
Сравнив уравнения (53.41) и (53.42), видим, что исключение незначимых главных компонент f ₄ и f ₅ , не отразилось на значениях коэффициентов уравнения b ₀ = 9,52, b ₁ = 0,93, b ₂ = 0,66 и соответствующих t_j ( j = 0, 1, 2, 3).

Это обусловлено некоррелированностью главных компонент. Здесь интересна параллель уравнений регрессии по исходным показателям (53.22), (53.23) и главным компонентам (53.41), (53.42).

Уравнение (53.42) значимо, поскольку F _набл = 194 > F_кр = 3,01, найденного при α = 0,05, v ₁ = 4, v ₂ = 16. Значимы и коэффициенты уравнения, так как t_j > t_кр. = 1,746, соответствующего α = 0,01, v = 16 для j = 0, 1, 2, 3. Коэффициент детерминации r = 0,486 свидетельствует о том, что 48,6% вариации у обусловлено влиянием трех первых главных компонент.

Уравнение (53.42) характеризуется средней относительной ошибкой аппроксимации 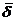= 9,99% и остаточной дисперсией s 2 = 1,91.

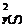
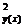
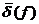
Уравнение регрессии на главных компонентах (53.42) обладает несколько лучшими аппроксимирующими свойствами по сравнению с регрессионной моделью (53.23) по исходным показателям: r = 0,486 > r = 0,469; = 9,99% (х) = 10,5% и s 2 ( f ) = 1,91 s 2 ( x ) = 1,97. Кроме того, в уравнении (53.42) главные компоненты являются линейными функциями всех исходных показателей, в то время как в уравнение (53.23) входят только две переменные ( x ₁ и х₄). В ряде случаев приходится учитывать, что модель (53.42) трудноинтерпретируема, так как в нее входит третья главная компонента f ₃ , которая нами не интерпретирована и вклад которой в суммарную дисперсию исходных показателей ( x ₁ , . х₅) составляет всего 8,6%. Однако исключение f ₃ из уравнения (53.42) значительно ухудшает аппроксимирующие свойства модели: r = 0,349; = 12,4% и s 2 (f ) = 2,41. Тогда в качестве регрессионной модели урожайности целесообразно выбрать уравнение (53.23).

Уравнение регрессии. Уравнение множественной регрессии

Во время учебы студенты очень часто сталкиваются с разнообразными уравнениями. Одно из них – уравнение регрессии — рассмотрено в данной статье. Такой тип уравнения применяется специально для описания характеристики связи между математическими параметрами. Данный вид равенств используют в статистике и эконометрике.

Определение понятия регрессии

В математике под регрессией подразумевается некая величина, описывающая зависимость среднего значения совокупности данных от значений другой величины. Уравнение регрессии показывает в качестве функции определенного признака среднее значение другого признака. Функция регрессии имеет вид простого уравнения у = х, в котором у выступает зависимой переменной, а х – независимой (признак-фактор). Фактически регрессия выражаться как у = f (x).

Какие бывают типы связей между переменными

В общем, выделяется два противоположных типа взаимосвязи: корреляционная и регрессионная.

Первая характеризуется равноправностью условных переменных. В данном случае достоверно не известно, какая переменная зависит от другой.

Если же между переменными не наблюдается равноправности и в условиях сказано, какая переменная объясняющая, а какая – зависимая, то можно говорить о наличии связи второго типа. Для того чтобы построить уравнение линейной регрессии, необходимо будет выяснить, какой тип связи наблюдается.

Виды регрессий

На сегодняшний день выделяют 7 разнообразных видов регрессии: гиперболическая, линейная, множественная, нелинейная, парная, обратная, логарифмически линейная.

Гиперболическая, линейная и логарифмическая

Уравнение линейной регрессии применяют в статистике для четкого объяснения параметров уравнения. Оно выглядит как у = с+т*х+Е. Гиперболическое уравнение имеет вид правильной гиперболы у = с + т / х + Е. Логарифмически линейное уравнение выражает взаимосвязь с помощью логарифмической функции: In у = In с + т* In x + In E.

Множественная и нелинейная

Два более сложных вида регрессии – это множественная и нелинейная. Уравнение множественной регрессии выражается функцией у = f(х₁ , х₂ . х_с)+E. В данной ситуации у выступает зависимой переменной, а х – объясняющей. Переменная Е — стохастическая, она включает влияние других факторов в уравнении. Нелинейное уравнение регрессии немного противоречиво. С одной стороны, относительно учтенных показателей оно не линейное, а с другой стороны, в роли оценки показателей оно линейное.

Обратные и парные виды регрессий

Обратная – это такой вид функции, который необходимо преобразовать в линейный вид. В самых традиционных прикладных программах она имеет вид функции у = 1/с + т*х+Е. Парное уравнение регрессии демонстрирует взаимосвязь между данными в качестве функции у = f (x) + Е. Точно так же, как и в других уравнениях, у зависит от х, а Е — стохастический параметр.

Понятие корреляции

Это показатель, демонстрирующий существование взаимосвязи двух явлений или процессов. Сила взаимосвязи выражается в качестве коэффициента корреляции. Его значение колеблется в рамках интервала [-1;+1]. Отрицательный показатель говорит о наличии обратной связи, положительный – о прямой. Если коэффициент принимает значение, равное 0, то взаимосвязи нет. Чем ближе значение к 1 – тем сильнее связь между параметрами, чем ближе к 0 – тем слабее.

Методы

Корреляционные параметрические методы могут оценить тесноту взаимосвязи. Их используют на базе оценки распределения для изучения параметров, подчиняющихся закону нормального распределения.

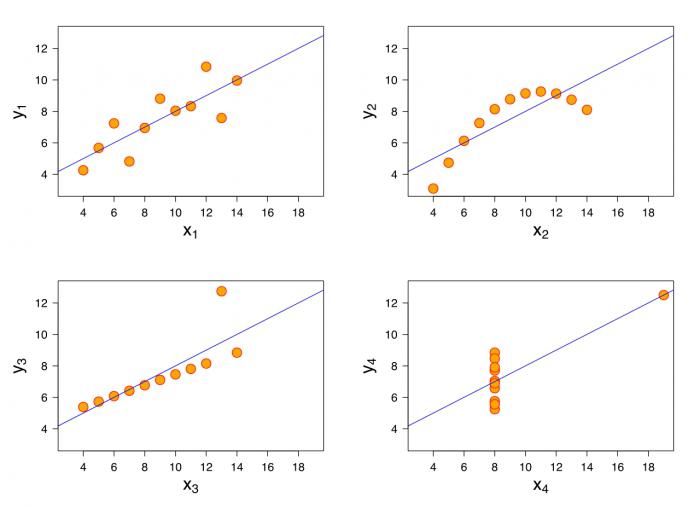
Параметры уравнения линейной регрессии необходимы для идентификации вида зависимости, функции регрессионного уравнения и оценивания показателей избранной формулы взаимосвязи. В качестве метода идентификации связи используется поле корреляции. Для этого все существующие данные необходимо изобразить графически. В прямоугольной двухмерной системе координат необходимо нанести все известные данные. Так образуется поле корреляции. Значение описывающего фактора отмечаются вдоль оси абсцисс, в то время как значения зависимого – вдоль оси ординат. Если между параметрами есть функциональная зависимость, они выстраиваются в форме линии.

В случае если коэффициент корреляции таких данных будет менее 30 %, можно говорить о практически полном отсутствии связи. Если он находится между 30 % и 70 %, то это говорит о наличии связей средней тесноты. 100 % показатель – свидетельство функциональной связи.

Нелинейное уравнение регрессии так же, как и линейное, необходимо дополнять индексом корреляции (R).

Корреляция для множественной регрессии

Коэффициент детерминации является показателем квадрата множественной корреляции. Он говорит о тесноте взаимосвязи представленного комплекса показателей с исследуемым признаком. Он также может говорить о характере влияния параметров на результат. Уравнение множественной регрессии оценивают с помощью этого показателя.

Для того чтобы вычислить показатель множественной корреляции, необходимо рассчитать его индекс.

Метод наименьших квадратов

Данный метод является способом оценивания факторов регрессии. Его суть заключается в минимизировании суммы отклонений в квадрате, полученных вследствие зависимости фактора от функции.

Парное линейное уравнение регрессии можно оценить с помощью такого метода. Этот тип уравнений используют в случае обнаружения между показателями парной линейной зависимости.

Параметры уравнений

Каждый параметр функции линейной регрессии несет определенный смысл. Парное линейное уравнение регрессии содержит два параметра: с и т. Параметр т демонстрирует среднее изменение конечного показателя функции у, при условии уменьшения (увеличения) переменной х на одну условную единицу. Если переменная х – нулевая, то функция равняется параметру с. Если же переменная х не нулевая, то фактор с не несет в себе экономический смысл. Единственное влияние на функцию оказывает знак перед фактором с. Если там минус, то можно сказать о замедленном изменении результата по сравнению с фактором. Если там плюс, то это свидетельствует об ускоренном изменении результата.

Каждый параметр, изменяющий значение уравнения регрессии, можно выразить через уравнение. Например, фактор с имеет вид с = y – тх.

Сгруппированные данные

Бывают такие условия задачи, в которых вся информация группируется по признаку x, но при этом для определенной группы указываются соответствующие средние значения зависимого показателя. В таком случае средние значения характеризуют, каким образом изменяется показатель, зависящий от х. Таким образом, сгруппированная информация помогает найти уравнение регрессии. Ее используют в качестве анализа взаимосвязей. Однако у такого метода есть свои недостатки. К сожалению, средние показатели достаточно часто подвергаются внешним колебаниям. Данные колебания не являются отображением закономерности взаимосвязи, они всего лишь маскируют ее «шум». Средние показатели демонстрируют закономерности взаимосвязи намного хуже, чем уравнение линейной регрессии. Однако их можно применять в виде базы для поиска уравнения. Перемножая численность отдельной совокупности на соответствующую среднюю можно получить сумму у в пределах группы. Далее необходимо подбить все полученные суммы и найти конечный показатель у. Чуть сложнее производить расчеты с показателем суммы ху. В том случае если интервалы малы, можно условно взять показатель х для всех единиц (в пределах группы) одинаковым. Следует перемножить его с суммой у, чтобы узнать сумму произведений x на у. Далее все суммы подбиваются вместе и получается общая сумма ху.

Множественное парное уравнение регрессии: оценка важности связи

Как рассматривалось ранее, множественная регрессия имеет функцию вида у = f (x₁,x₂,…,x_m)+E. Чаще всего такое уравнение используют для решения проблемы спроса и предложения на товар, процентного дохода по выкупленным акциям, изучения причин и вида функции издержек производства. Ее также активно применяют в самых разнообразным макроэкономических исследованиях и расчетах, а вот на уровне микроэкономики такое уравнение применяют немного реже.

Основной задачей множественной регрессии является построение модели данных, содержащих огромное количество информации, для того чтобы в дальнейшем определить, какое влияние имеет каждый из факторов по отдельности и в их общей совокупности на показатель, который необходимо смоделировать, и его коэффициенты. Уравнение регрессии может принимать самые разнообразные значения. При этом для оценки взаимосвязи обычно используется два типа функций: линейная и нелинейная.

Линейная функция изображается в форме такой взаимосвязи: у = а₀ + a₁х₁ + а₂х₂,+ . + a_mx_m. При этом _а2, a_m, считаются коэффициентами «чистой» регрессии. Они необходимы для характеристики среднего изменения параметра у с изменением (уменьшением или увеличением) каждого соответствующего параметра х на одну единицу, с условием стабильного значения других показателей.

Нелинейные уравнения имеют, к примеру, вид степенной функции у=ах₁ b1 х₂ b2 . x_m bm . В данном случае показатели b₁, b₂. b_m – называются коэффициентами эластичности, они демонстрируют, каким образом изменится результат (на сколько %) при увеличении (уменьшении) соответствующего показателя х на 1 % и при стабильном показателе остальных факторов.

Какие факторы необходимо учитывать при построении множественной регрессии

Для того чтобы правильно построить множественную регрессию, необходимо выяснить, на какие именно факторы следует обратить особое внимание.

Необходимо иметь определенное понимание природы взаимосвязей между экономическими факторами и моделируемым. Факторы, которые необходимо будет включать, обязаны отвечать следующим признакам:

• Должны быть подвластны количественному измерению. Для того чтобы использовать фактор, описывающий качество предмета, в любом случае следует придать ему количественную форму.
• Не должна присутствовать интеркорреляция факторов, или функциональная взаимосвязь. Такие действия чаще всего приводят к необратимым последствиям – система обыкновенных уравнений становится не обусловленной, а это влечет за собой ее ненадежность и нечеткость оценок.
• В случае существования огромного показателя корреляции не существует способа для выяснения изолированного влияния факторов на окончательный результат показателя, следовательно, коэффициенты становятся неинтерпретируемыми.

Методы построения

Существует огромное количество методов и способов, объясняющих, каким образом можно выбрать факторы для уравнения. Однако все эти методы строятся на отборе коэффициентов с помощью показателя корреляции. Среди них выделяют:

• Способ исключения.
• Способ включения.
• Пошаговый анализ регрессии.

Первый метод подразумевает отсев всех коэффициентов из совокупного набора. Второй метод включает введение множества дополнительных факторов. Ну а третий – отсев факторов, которые были ранее применены для уравнения. Каждый из этих методов имеет право на существование. У них есть свои плюсы и минусы, но они все по-своему могут решить вопрос отсева ненужных показателей. Как правило, результаты, полученные каждым отдельным методом, достаточно близки.

Методы многомерного анализа

Такие способы определения факторов базируются на рассмотрении отдельных сочетаний взаимосвязанных признаков. Они включают в себя дискриминантный анализ, распознание обликов, способ главных компонент и анализ кластеров. Кроме того, существует также факторный анализ, однако он появился вследствие развития способа компонент. Все они применяются в определенных обстоятельствах, при наличии определенных условий и факторов.

Уравнение регрессии на главных компонентах

Когда переменных немного или имеются некоторые априорные теоретические данные, выбор таких комбинаций может быть осуществлен из содержательных соображений в более общей ситуации один из возможных подходов основывается на использовании так называемых главных компонент (см. [14, п. 10.5.2]), что приводит к регрессии на главные компоненты [195, 201, 219]. [c.255]

Вернемся к регрессии на главные компоненты Z = (2 . [c.267]

Оценивание параметров уравнения регрессии в случае сильной мультиколлинеарности основано на различных методах регуляризации задачи — модификациях регрессии на главные компоненты, гребневых и редуцированных оценках. Со статистической точки зрения получаемые оценки являются, в отличие от мнк-оценок, смещенными. Однако они обладают рядом оптимальных свойств, в частности обеспечивают лучшие прогностические свойства оцененного уравнения регрессии на объектах, не вошедших в обучающую выборку. [c.297]

Свободный член уравнения, построенного на главных компонентах, характеризует среднее значение прибыли в анализируемой совокупности. В силу этого решение уравнения регрессии, построенного на главных компонентах, позволяет определить величину прибыли только за счет выделения главных компонент. Наличие в уравнении значения прибыли дает возможность проводить сравнительный анализ работы предприятия за несколько лет, установить динамику его рентабельности. [c.152]

Снова возникает задача оценки параметров уравнения множественной регрессии. Действительно, исходя из экономического смысла значения (/ = 1 >. 14) представляют собой агрегированные экономические показатели, которые находятся в тесной взаимосвязи и взаимозависимости. Изменение одного из них ведет к изменению всех остальных. Это выводит на проблему мультиколлинеарности, вызванную экономическим содержанием задачи. Для разрешения этой проблемы используется метод главных компонент. Суть метода — сократить число объясняющих переменных до наиболее существенно влияющих факторов. [c.314]

Другой метод выбора числа компонент основан на общепринятой методологии использования главных компонент. Задаемся некоторой величиной доли следа а, близкой к 1, и включаем в уравнение регрессии компоненты до тех пор, пока [c.258]

Однако процедуры отбора главных компонент, основанные на /-и F-статистиках, правильнее нацелены на решение сущности задачи, хотя при их использовании могут быть отброшены и некоторые главные компоненты, соответствующие большим значениям Kt (если они слабо коррелированы с переменной у). Правда, как правило, компоненты с малыми значениями собственных чисел оказываются одновременно и слабо коррелированными с у и также отбрасываются, так что отбор существенных главных компонент по этим критериям автоматически приводит и к регуляризации задачи. Зная включенные в уравнение компоненты и соответствующие им коэффициенты регрессии, легко найти коэффициенты регрессии относительно исходных переменных [c.258]

Отбор существенных переменных в пространстве главных компонент рассмотрен в п. 8.3. Как там показано, он приводит к следующим результатам с одной стороны, к некоторому увеличению наблюдаемого значения нормированной суммы квадратов отклонений Д , но одновременно к уменьшению средне-квадратического отклонения от соответствующих истинных значений параметров и к уменьшению средней ошибки прогноза для векторов X, не входящих в матрицу плана X (т. е. в обучающую выборку, см. п. 11.3). Последнего можно достичь и при отборе существенных переменных в исходном пространстве (опять-таки за счет увеличения нормированной суммы квадратов отклонений на обучающей выборке). Фактически отбор переменных означает, что исходное множество из р переменных делится на два подмножества X (р—q) и X (q), состоящих из таких р — q и q переменных, что коэффициенты регрессии при р — q переменных, входящих в первое подмножество, полагаются равными нулю, а коэффициенты при q переменных из второго подмножества оцениваются по мнк (по окончании процедуры отбора для оценки можно использовать и методы, изложенные в 8.2—8.5). [c.280]

Для устранения мультиколлинеарности может быть использован переход от исходных объясняющих переменных Х, А . Х , связанных между собой достаточно тесной корреляционной зависимостью, к новым переменным, представляющим линейные комбинации исходных. При этом новые переменные должны быть слабокоррелированными либо вообще некоррелированными. В качестве таких переменных берут, например, так называемые главные компоненты вектора исходных объясняющих переменных, изучаемые в компонентном анализе, и рассматривают регрессию на главных компонентах,. в которой последние выступают в качестве обобщенных объясняющих переменных, подлежащих в дальнейшем содержательной (экономической) интерпретации. [c.111]

Анализ долученных регрессионных моделей на основе фактсров-пре-юндентов до ка дой компоненте доказал, что их статистические оценки хуже, нежели исходных уравнений регрессии на главных компонентах (в статье не приводятся). В силу вышеизложенного мы исключили эти модели из дальнейшего анализа с альтернативными вариантами, [c.12]

VrikjvW (у = 9 р Тогда согласно формуле (8.30) оценка Джеймса — Стейна для параметров уравнения регрессии на главные компоненты будет иметь в точности вид (8.36). т. е. [c.264]

Регрессия на главные компоненты. Веса щ могут принимать одно из двух значений щ — 1, если выполняется какое-либо из условий информативности данной главной компоненты (см. п. 8.2), либо a,i = 0, если данная компонента удаляется. Заметим, что редуцированные оценки Джеймса — Стейна И [c.269]

Второй путь, позволяющий использовать главные компоненты, вну-дает меньше доверия и требует усилий, превосходящих ожидаемый эффект2. Он относится к случаю, когда проблема заключена не в чрезмерном количестве переменных X, а в наличии мультиколлинеарно-сти. Как хорошо известно, оценки наименьших квадратов для коэффициентов при переменных X выглядят очень убедительно. Кендалл предлагает вычислить главные компоненты на основе переменных X, от-эросить те из них, которые соответствуют низким значениям характеристических корней, найти регрессию Y на оставшиеся главные компоненты, а затем с помощью обратного преобразования вернуться от коэффициентов регрессии на главные компоненты к оценкам коэффициентов при переменных X. Предположим, например, что имеются пять переменных X, что мы вычислили главные компоненты и ограничи-пись только двумя из них [c.329]

Для регрессии у на главные компоненты и на исходные переменные оценки типа (8.40) лучше оценки Джеймса — Стейна и мнк-оценки по соответственно взвешенным критериям L и [c.265]

Оценка влияния кавдого из перечисленных факторов имеет ванное значение в процессе (экономического анализа формирования уровня производительности труда в буровых организациях объединения. С точки зреняя исследуемой обобщенной характеристики высокая степень концентрации производства достигается при дальнейшем (перспективном) росте фондовооруженности и производительного времени. Сопоставительный анализ приведенных зависимостей, полученных в результате исследования, показывает, что выражение ( I ) может рассматриваться в качестве экономико-математической модели процесса формирования производительности труда в условиях АСУ. Она характеризуется удовлетворительными коэффициентами регрессии при исследуемых факторах все направленные воздействия этих факторов соответствуют логике их влияния на процесс формирования производительности труда. С точка зрения количественных характеристик, оценки уровня дисперсии (95%) модель является удовлетворительной. Средняя относительная ошибка аппроксимации уравнения, полученного методом главных компонент, составляет [c.11]

Вопрос о выборе способа численного решения имеет смысл лишь в том случае, когда погрешность вычисления оценок коэффициентов регрессии на ЭВМ сравнима по величине с их статистическим разбросом, который определяется формулой (8.8). Необходимым для этого условием, как мы увидим далее, является наличие мультиколлинеарности. Но при выраженной мультиколлинеарности с точки зрения статистической устойчивости оценок лучше переходить к решению регуляризован-ных (тем или иным способом) систем уравнений (8.60), (8.60 ), (8.60″), (8.60″ ). Для систем нормальных уравнений методами регуляризации будут уже рассмотренные метод главных компонент (см. 8.2) и гребневая регрессия (см. 8.5). 8.6.2. Оценки величин возмущений для решений центрированной и соответствующей ей нормальной системы уравнений. Пусть А в = С некоторая система линейных уравнений, матрица А которой имеет размерность q X k (k не обязательно равно q), 6 — вектор размерности fe, правая часть С — вектор размерности q. [c.273]