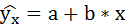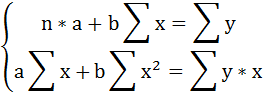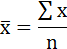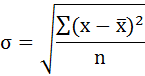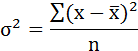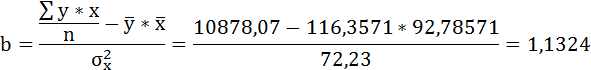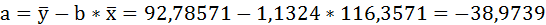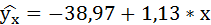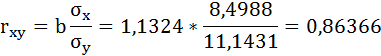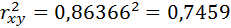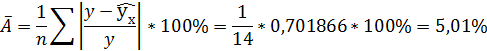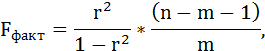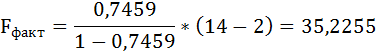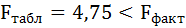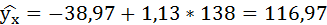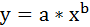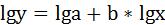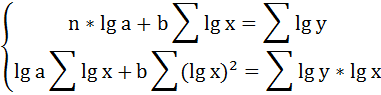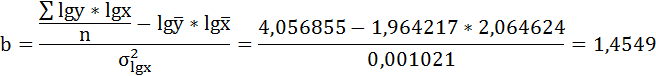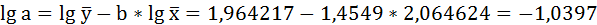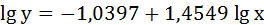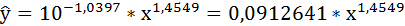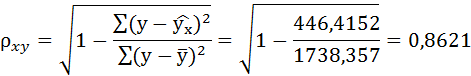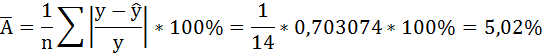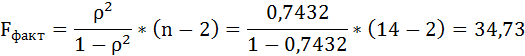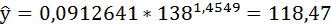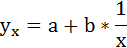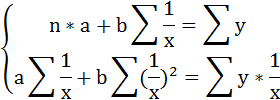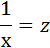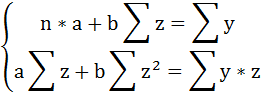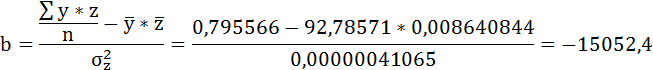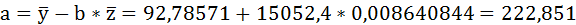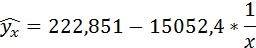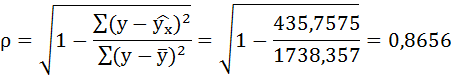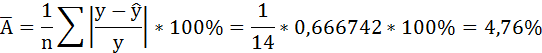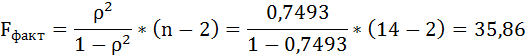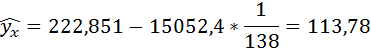Корреляция и регрессия
Линейное уравнение регрессии имеет вид y=bx+a+ε
Здесь ε — случайная ошибка (отклонение, возмущение).
Причины существования случайной ошибки:
1. Невключение в регрессионную модель значимых объясняющих переменных;
2. Агрегирование переменных. Например, функция суммарного потребления – это попытка общего выражения совокупности решений отдельных индивидов о расходах. Это лишь аппроксимация отдельных соотношений, которые имеют разные параметры.
3. Неправильное описание структуры модели;
4. Неправильная функциональная спецификация;
5. Ошибки измерения.
Так как отклонения εi для каждого конкретного наблюдения i – случайны и их значения в выборке неизвестны, то:
1) по наблюдениям xi и yi можно получить только оценки параметров α и β
2) Оценками параметров α и β регрессионной модели являются соответственно величины а и b, которые носят случайный характер, т.к. соответствуют случайной выборке;
Тогда оценочное уравнение регрессии (построенное по выборочным данным) будет иметь вид y = bx + a + ε, где ei – наблюдаемые значения (оценки) ошибок εi, а и b соответственно оценки параметров α и β регрессионной модели, которые следует найти.
Для оценки параметров α и β — используют МНК (метод наименьших квадратов).
Система нормальных уравнений.
Для наших данных система уравнений имеет вид:
10a + 356b = 49
356a + 2135b = 9485
Из первого уравнения выражаем а и подставим во второе уравнение
Получаем b = 68.16, a = 11.17
Уравнение регрессии:
y = 68.16 x — 11.17
1. Параметры уравнения регрессии.
Выборочные средние.
1.1. Коэффициент корреляции
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 Y фактором X весьма высокая и прямая.
1.2. Уравнение регрессии (оценка уравнения регрессии).
Линейное уравнение регрессии имеет вид y = 68.16 x -11.17
Коэффициентам уравнения линейной регрессии можно придать экономический смысл. Коэффициент уравнения регрессии показывает, на сколько ед. изменится результат при изменении фактора на 1 ед.
Коэффициент b = 68.16 показывает среднее изменение результативного показателя (в единицах измерения у ) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y повышается в среднем на 68.16.
Коэффициент a = -11.17 формально показывает прогнозируемый уровень у , но только в том случае, если х=0 находится близко с выборочными значениями.
Но если х=0 находится далеко от выборочных значений x , то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.
Подставив в уравнение регрессии соответствующие значения x , можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.
Связь между у и x определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе — обратная). В нашем примере связь прямая.
1.3. Коэффициент эластичности.
Коэффициенты регрессии (в примере b) нежелательно использовать для непосредственной оценки влияния факторов на результативный признак в том случае, если существует различие единиц измерения результативного показателя у и факторного признака х.
Для этих целей вычисляются коэффициенты эластичности и бета — коэффициенты. Коэффициент эластичности находится по формуле:
Он показывает, на сколько процентов в среднем изменяется результативный признак у при изменении факторного признака х на 1%. Он не учитывает степень колеблемости факторов.
В нашем примере коэффициент эластичности больше 1. Следовательно, при изменении Х на 1%, Y изменится более чем на 1%. Другими словами — Х существенно влияет на Y.
Бета – коэффициент показывает, на какую часть величины своего среднего квадратичного отклонения изменится в среднем значение результативного признака при изменении факторного признака на величину его среднеквадратического отклонения при фиксированном на постоянном уровне значении остальных независимых переменных:
Т.е. увеличение x на величину среднеквадратического отклонения этого показателя приведет к увеличению среднего Y на 0.9796 среднеквадратичного отклонения этого показателя.
1.4. Ошибка аппроксимации.
Оценим качество уравнения регрессии с помощью ошибки абсолютной аппроксимации.
Поскольку ошибка больше 15%, то данное уравнение не желательно использовать в качестве регрессии.
1.6. Коэффициент детерминации.
Квадрат (множественного) коэффициента корреляции называется коэффициентом детерминации, который показывает долю вариации результативного признака, объясненную вариацией факторного признака.
Чаще всего, давая интерпретацию коэффициента детерминации, его выражают в процентах.
R 2 = 0.98 2 = 0.9596, т.е. в 95.96 % случаев изменения x приводят к изменению у . Другими словами — точность подбора уравнения регрессии — высокая. Остальные 4.04 % изменения Y объясняются факторами, не учтенными в модели.
| x | y | x 2 | y 2 | x·y | y(x) | (yi— y ) 2 | (y-y(x)) 2 | (xi— x ) 2 | |y — yx|:y |
| 0.371 | 15.6 | 0.1376 | 243.36 | 5.79 | 14.11 | 780.89 | 2.21 | 0.1864 | 0.0953 |
| 0.399 | 19.9 | 0.1592 | 396.01 | 7.94 | 16.02 | 559.06 | 15.04 | 0.163 | 0.1949 |
| 0.502 | 22.7 | 0.252 | 515.29 | 11.4 | 23.04 | 434.49 | 0.1176 | 0.0905 | 0.0151 |
| 0.572 | 34.2 | 0.3272 | 1169.64 | 19.56 | 27.81 | 87.32 | 40.78 | 0.0533 | 0.1867 |
| 0.607 | 44.5 | .3684 | 1980.25 | 27.01 | 30.2 | 0.9131 | 204.49 | 0.0383 | 0.3214 |
| 0.655 | 26.8 | 0.429 | 718.24 | 17.55 | 33.47 | 280.38 | 44.51 | 0.0218 | 0.2489 |
| 0.763 | 35.7 | 0.5822 | 1274.49 | 27.24 | 40.83 | 61.54 | 26.35 | 0.0016 | 0.1438 |
| 0.873 | 30.6 | 0.7621 | 936.36 | 26.71 | 48.33 | 167.56 | 314.39 | 0.0049 | 0.5794 |
| 2.48 | 161.9 | 6.17 | 26211.61 | 402 | 158.07 | 14008.04 | 14.66 | 2.82 | 0.0236 |
| 7.23 | 391.9 | 9.18 | 33445.25 | 545.2 | 391.9 | 16380.18 | 662.54 | 3.38 | 1.81 |
2. Оценка параметров уравнения регрессии.
2.1. Значимость коэффициента корреляции.
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=7 находим tкрит:
tкрит = (7;0.05) = 1.895
где m = 1 — количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически — значим
В парной линейной регрессии t 2 r = t 2 b и тогда проверка гипотез о значимости коэффициентов регрессии и корреляции равносильна проверке гипотезы о существенности линейного уравнения регрессии.
2.3. Анализ точности определения оценок коэффициентов регрессии.
Несмещенной оценкой дисперсии возмущений является величина:
S 2 y = 94.6484 — необъясненная дисперсия (мера разброса зависимой переменной вокруг линии регрессии).
Sy = 9.7287 — стандартная ошибка оценки (стандартная ошибка регрессии).
S a — стандартное отклонение случайной величины a.
Sb — стандартное отклонение случайной величины b.
2.4. Доверительные интервалы для зависимой переменной.
Экономическое прогнозирование на основе построенной модели предполагает, что сохраняются ранее существовавшие взаимосвязи переменных и на период упреждения.
Для прогнозирования зависимой переменной результативного признака необходимо знать прогнозные значения всех входящих в модель факторов.
Прогнозные значения факторов подставляют в модель и получают точечные прогнозные оценки изучаемого показателя. (a + bxp ± ε) где
Рассчитаем границы интервала, в котором будет сосредоточено 95% возможных значений Y при неограниченно большом числе наблюдений и X p = 1 (-11.17 + 68.16*1 ± 6.4554)
(50.53;63.44)
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
Индивидуальные доверительные интервалы для Y при данном значении X.
(a + bx i ± ε)
где
| xi | y = -11.17 + 68.16xi | εi | ymin | ymax |
| 0.371 | 14.11 | 19.91 | -5.8 | 34.02 |
| 0.399 | 16.02 | 19.85 | -3.83 | 35.87 |
| 0.502 | 23.04 | 19.67 | 3.38 | 42.71 |
| 0.572 | 27.81 | 19.57 | 8.24 | 47.38 |
| 0.607 | 30.2 | 19.53 | 10.67 | 49.73 |
| 0.655 | 33.47 | 19.49 | 13.98 | 52.96 |
| 0.763 | 40.83 | 19.44 | 21.4 | 60.27 |
| 0.873 | 48.33 | 19.45 | 28.88 | 67.78 |
| 2.48 | 158.07 | 25.72 | 132.36 | 183.79 |
С вероятностью 95% можно гарантировать, что значения Y при неограниченно большом числе наблюдений не выйдет за пределы найденных интервалов.
2.5. Проверка гипотез относительно коэффициентов линейного уравнения регрессии.
1) t-статистика. Критерий Стьюдента.
Проверим гипотезу H0 о равенстве отдельных коэффициентов регрессии нулю (при альтернативе H1 не равно) на уровне значимости α=0.05.
tкрит = (7;0.05) = 1.895
Поскольку 12.8866 > 1.895, то статистическая значимость коэффициента регрессии b подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Поскольку 2.0914 > 1.895, то статистическая значимость коэффициента регрессии a подтверждается (отвергаем гипотезу о равенстве нулю этого коэффициента).
Доверительный интервал для коэффициентов уравнения регрессии.
Определим доверительные интервалы коэффициентов регрессии, которые с надежность 95% будут следующими:
(b — tкрит Sb; b + tкрит Sb)
(68.1618 — 1.895 • 5.2894; 68.1618 + 1.895 • 5.2894)
(58.1385;78.1852)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
(a — ta)
(-11.1744 — 1.895 • 5.3429; -11.1744 + 1.895 • 5.3429)
(-21.2992;-1.0496)
С вероятностью 95% можно утверждать, что значение данного параметра будут лежать в найденном интервале.
2) F-статистики. Критерий Фишера.
Проверка значимости модели регрессии проводится с использованием F-критерия Фишера, расчетное значение которого находится как отношение дисперсии исходного ряда наблюдений изучаемого показателя и несмещенной оценки дисперсии остаточной последовательности для данной модели.
Если расчетное значение с lang=EN-US>n-m-1) степенями свободы больше табличного при заданном уровне значимости, то модель считается значимой.
где m – число факторов в модели.
Оценка статистической значимости парной линейной регрессии производится по следующему алгоритму:
1. Выдвигается нулевая гипотеза о том, что уравнение в целом статистически незначимо: H0: R 2 =0 на уровне значимости α.
2. Далее определяют фактическое значение F-критерия:
где m=1 для парной регрессии.
3. Табличное значение определяется по таблицам распределения Фишера для заданного уровня значимости, принимая во внимание, что число степеней свободы для общей суммы квадратов (большей дисперсии) равно 1 и число степеней свободы остаточной суммы квадратов (меньшей дисперсии) при линейной регрессии равно n-2.
4. Если фактическое значение F-критерия меньше табличного, то говорят, что нет основания отклонять нулевую гипотезу.
В противном случае, нулевая гипотеза отклоняется и с вероятностью (1-α) принимается альтернативная гипотеза о статистической значимости уравнения в целом.
Табличное значение критерия со степенями свободы k1=1 и k2=7, Fkp = 5.59
Поскольку фактическое значение F > Fkp, то коэффициент детерминации статистически значим (Найденная оценка уравнения регрессии статистически надежна).
Проверка на наличие автокорреляции остатков.
Важной предпосылкой построения качественной регрессионной модели по МНК является независимость значений случайных отклонений от значений отклонений во всех других наблюдениях. Это гарантирует отсутствие коррелированности между любыми отклонениями и, в частности, между соседними отклонениями.
Автокорреляция (последовательная корреляция) определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или в пространстве (перекрестные ряды). Автокорреляция остатков (отклонений) обычно встречается в регрессионном анализе при использовании данных временных рядов и очень редко при использовании перекрестных данных.
В экономических задачах значительно чаще встречается положительная автокорреляция, нежели отрицательная автокорреляция. В большинстве случаев положительная автокорреляция вызывается направленным постоянным воздействием некоторых неучтенных в модели факторов.
Отрицательная автокорреляция фактически означает, что за положительным отклонением следует отрицательное и наоборот. Такая ситуация может иметь место, если ту же зависимость между спросом на прохладительные напитки и доходами рассматривать по сезонным данным (зима-лето).
Среди основных причин, вызывающих автокорреляцию, можно выделить следующие:
1. Ошибки спецификации. Неучет в модели какой-либо важной объясняющей переменной либо неправильный выбор формы зависимости обычно приводят к системным отклонениям точек наблюдения от линии регрессии, что может обусловить автокорреляцию.
2. Инерция. Многие экономические показатели (инфляция, безработица, ВНП и т.д.) обладают определенной цикличностью, связанной с волнообразностью деловой активности. Поэтому изменение показателей происходит не мгновенно, а обладает определенной инертностью.
3. Эффект паутины. Во многих производственных и других сферах экономические показатели реагируют на изменение экономических условий с запаздыванием (временным лагом).
4. Сглаживание данных. Зачастую данные по некоторому продолжительному временному периоду получают усреднением данных по составляющим его интервалам. Это может привести к определенному сглаживанию колебаний, которые имелись внутри рассматриваемого периода, что в свою очередь может служить причиной автокорреляции.
Последствия автокорреляции схожи с последствиями гетероскедастичности: выводы по t- и F-статистикам, определяющие значимость коэффициента регрессии и коэффициента детерминации, возможно, будут неверными.
Обнаружение автокорреляции
1. Графический метод
Есть ряд вариантов графического определения автокорреляции. Один из них увязывает отклонения ei с моментами их получения i. При этом по оси абсцисс откладывают либо время получения статистических данных, либо порядковый номер наблюдения, а по оси ординат – отклонения ei (либо оценки отклонений).
Естественно предположить, что если имеется определенная связь между отклонениями, то автокорреляция имеет место. Отсутствие зависимости скоре всего будет свидетельствовать об отсутствии автокорреляции.
Автокорреляция становится более наглядной, если построить график зависимости ei от ei-1.
Задача №1 Построение уравнения регрессии
Имеются следующие данные разных стран об индексе розничных цен на продукты питания (х) и об индексе промышленного производства (у).
| Индекс розничных цен на продукты питания (х) | Индекс промышленного производства (у) | |
|---|---|---|
| 1 | 100 | 70 |
| 2 | 105 | 79 |
| 3 | 108 | 85 |
| 4 | 113 | 84 |
| 5 | 118 | 85 |
| 6 | 118 | 85 |
| 7 | 110 | 96 |
| 8 | 115 | 99 |
| 9 | 119 | 100 |
| 10 | 118 | 98 |
| 11 | 120 | 99 |
| 12 | 124 | 102 |
| 13 | 129 | 105 |
| 14 | 132 | 112 |
Требуется:
1. Для характеристики зависимости у от х рассчитать параметры следующих функций:
В) равносторонней гиперболы.
2. Для каждой модели рассчитать показатели: тесноты связи и среднюю ошибку аппроксимации.
3. Оценить статистическую значимость параметров регрессии и корреляции.
4. Выполнить прогноз значения индекса промышленного производства у при прогнозном значении индекса розничных цен на продукты питания х=138.
Решение:
1. Для расчёта параметров линейной регрессии
Решаем систему нормальных уравнений относительно a и b:
Построим таблицу расчётных данных, как показано в таблице 1.
Таблица 1 Расчетные данные для оценки линейной регрессии
| № п/п | х | у | ху | x 2 | y 2 |  |  |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 7000 | 10000 | 4900 | 74,26340 | 0,060906 |
| 2 | 105 | 79 | 8295 | 11025 | 6241 | 79,92527 | 0,011712 |
| 3 | 108 | 85 | 9180 | 11664 | 7225 | 83,32238 | 0,019737 |
| 4 | 113 | 84 | 9492 | 12769 | 7056 | 88,98425 | 0,059336 |
| 5 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 6 | 118 | 85 | 10030 | 13924 | 7225 | 94,64611 | 0,113484 |
| 7 | 110 | 96 | 10560 | 12100 | 9216 | 85,58713 | 0,108467 |
| 8 | 115 | 99 | 11385 | 13225 | 9801 | 91,24900 | 0,078293 |
| 9 | 119 | 100 | 11900 | 14161 | 10000 | 95,77849 | 0,042215 |
| 10 | 118 | 98 | 11564 | 13924 | 9604 | 94,64611 | 0,034223 |
| 11 | 120 | 99 | 11880 | 14400 | 9801 | 96,91086 | 0,021102 |
| 12 | 124 | 102 | 12648 | 15376 | 10404 | 101,4404 | 0,005487 |
| 13 | 129 | 105 | 13545 | 16641 | 11025 | 107,1022 | 0,020021 |
| 14 | 132 | 112 | 14784 | 17424 | 12544 | 110,4993 | 0,013399 |
| Итого: | 1629 | 1299 | 152293 | 190557 | 122267 | 1299,001 | 0,701866 |
| Среднее значение: | 116,3571 | 92,78571 | 10878,07 | 13611,21 | 8733,357 | х | х |
 | 8,4988 | 11,1431 | х | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х | х |
Среднее значение определим по формуле:
Cреднее квадратическое отклонение рассчитаем по формуле:
и занесём полученный результат в таблицу 1.
Возведя в квадрат полученное значение получим дисперсию:
Параметры уравнения можно определить также и по формулам:
Таким образом, уравнение регрессии:
Следовательно, с увеличением индекса розничных цен на продукты питания на 1, индекс промышленного производства увеличивается в среднем на 1,13.
Рассчитаем линейный коэффициент парной корреляции:
Связь прямая, достаточно тесная.
Определим коэффициент детерминации:
Вариация результата на 74,59% объясняется вариацией фактора х.
Подставляя в уравнение регрессии фактические значения х, определим теоретические (расчётные) значения 
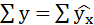
следовательно, параметры уравнения определены правильно.
Рассчитаем среднюю ошибку аппроксимации – среднее отклонение расчётных значений от фактических:
В среднем расчётные значения отклоняются от фактических на 5,01%.
Оценку качества уравнения регрессии проведём с помощью F-теста.
F-тест состоит в проверке гипотезы Н0 о статистической незначимости уравнения регрессии и показателя тесноты связи. Для этого выполняется сравнение фактического Fфакт и критического (табличного) Fтабл значений F-критерия Фишера.
Fфакт определяется по формуле:
где n – число единиц совокупности;
m – число параметров при переменных х.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза.
Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
2. Степенная регрессия имеет вид:
Для определения параметров производят логарифмирование степенной функции:
Для определения параметров логарифмической функции строят систему нормальных уравнений по способу наименьших квадратов:
Построим таблицу расчётных данных, как показано в таблице 2.
Таблица 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у | lg x | lg y | lg x*lg y | (lg x) 2 | (lg y) 2 |
|---|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 2,000000 | 1,845098 | 3,690196 | 4,000000 | 3,404387 |
| 2 | 105 | 79 | 2,021189 | 1,897627 | 3,835464 | 4,085206 | 3,600989 |
| 3 | 108 | 85 | 2,033424 | 1,929419 | 3,923326 | 4,134812 | 3,722657 |
| 4 | 113 | 84 | 2,053078 | 1,924279 | 3,950696 | 4,215131 | 3,702851 |
| 5 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 6 | 118 | 85 | 2,071882 | 1,929419 | 3,997528 | 4,292695 | 3,722657 |
| 7 | 110 | 96 | 2,041393 | 1,982271 | 4,046594 | 4,167284 | 3,929399 |
| 8 | 115 | 99 | 2,060698 | 1,995635 | 4,112401 | 4,246476 | 3,982560 |
| 9 | 119 | 100 | 2,075547 | 2,000000 | 4,151094 | 4,307895 | 4,000000 |
| 10 | 118 | 98 | 2,071882 | 1,991226 | 4,125585 | 4,292695 | 3,964981 |
| 11 | 120 | 99 | 2,079181 | 1,995635 | 4,149287 | 4,322995 | 3,982560 |
| 12 | 124 | 102 | 2,093422 | 2,008600 | 4,204847 | 4,382414 | 4,034475 |
| 13 | 129 | 105 | 2,110590 | 2,021189 | 4,265901 | 4,454589 | 4,085206 |
| 14 | 132 | 112 | 2,120574 | 2,049218 | 4,345518 | 4,496834 | 4,199295 |
| Итого | 1629 | 1299 | 28,90474 | 27,49904 | 56,79597 | 59,69172 | 54,05467 |
| Среднее значение | 116,3571 | 92,78571 | 2,064624 | 1,964217 | 4,056855 | 4,263694 | 3,861048 |
 | 8,4988 | 11,1431 | 0,031945 | 0,053853 | х | х | х |
 | 72,23 | 124,17 | 0,001021 | 0,0029 | х | х | х |
Продолжение таблицы 2 Расчетные данные для оценки степенной регрессии
| №п/п | х | у |  |  |  |  |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 74,16448 | 17,34292 | 0,059493 | 519,1886 |
| 2 | 105 | 79 | 79,62057 | 0,385112 | 0,007855 | 190,0458 |
| 3 | 108 | 85 | 82,95180 | 4,195133 | 0,024096 | 60,61728 |
| 4 | 113 | 84 | 88,59768 | 21,13866 | 0,054734 | 77,1887 |
| 5 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 6 | 118 | 85 | 94,35840 | 87,57961 | 0,110099 | 60,61728 |
| 7 | 110 | 96 | 85,19619 | 116,7223 | 0,11254 | 10,33166 |
| 8 | 115 | 99 | 90,88834 | 65,79901 | 0,081936 | 38,6174 |
| 9 | 119 | 100 | 95,52408 | 20,03384 | 0,044759 | 52,04598 |
| 10 | 118 | 98 | 94,35840 | 13,26127 | 0,037159 | 27,18882 |
| 11 | 120 | 99 | 96,69423 | 5,316563 | 0,023291 | 38,6174 |
| 12 | 124 | 102 | 101,4191 | 0,337467 | 0,005695 | 84,90314 |
| 13 | 129 | 105 | 107,4232 | 5,872099 | 0,023078 | 149,1889 |
| 14 | 132 | 112 | 111,0772 | 0,85163 | 0,00824 | 369,1889 |
| Итого | 1629 | 1299 | 1296,632 | 446,4152 | 0,703074 | 1738,357 |
| Среднее значение | 116,3571 | 92,78571 | х | х | х | х |
 | 8,4988 | 11,1431 | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х |
Решая систему нормальных уравнений, определяем параметры логарифмической функции.
Получим линейное уравнение:
Выполнив его потенцирование, получим:
Подставляя в данное уравнение фактические значения х, получаем теоретические значения результата 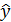
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 5,02%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
3. Уравнение равносторонней гиперболы
Для определения параметров этого уравнения используется система нормальных уравнений:
Произведем замену переменных
и получим следующую систему нормальных уравнений:
Решая систему нормальных уравнений, определяем параметры гиперболы.
Составим таблицу расчётных данных, как показано в таблице 3.
Таблица 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у | z | yz | 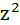 | 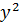 |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 0,010000000 | 0,700000 | 0,0001000 | 4900 |
| 2 | 105 | 79 | 0,009523810 | 0,752381 | 0,0000907 | 6241 |
| 3 | 108 | 85 | 0,009259259 | 0,787037 | 0,0000857 | 7225 |
| 4 | 113 | 84 | 0,008849558 | 0,743363 | 0,0000783 | 7056 |
| 5 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 6 | 118 | 85 | 0,008474576 | 0,720339 | 0,0000718 | 7225 |
| 7 | 110 | 96 | 0,009090909 | 0,872727 | 0,0000826 | 9216 |
| 8 | 115 | 99 | 0,008695652 | 0,860870 | 0,0000756 | 9801 |
| 9 | 119 | 100 | 0,008403361 | 0,840336 | 0,0000706 | 10000 |
| 10 | 118 | 98 | 0,008474576 | 0,830508 | 0,0000718 | 9604 |
| 11 | 120 | 99 | 0,008333333 | 0,825000 | 0,0000694 | 9801 |
| 12 | 124 | 102 | 0,008064516 | 0,822581 | 0,0000650 | 10404 |
| 13 | 129 | 105 | 0,007751938 | 0,813953 | 0,0000601 | 11025 |
| 14 | 132 | 112 | 0,007575758 | 0,848485 | 0,0000574 | 12544 |
| Итого: | 1629 | 1299 | 0,120971823 | 11,13792 | 0,0010510 | 122267 |
| Среднее значение: | 116,3571 | 92,78571 | 0,008640844 | 0,795566 | 0,0000751 | 8733,357 |
 | 8,4988 | 11,1431 | 0,000640820 | х | х | х |
 | 72,23 | 124,17 | 0,000000411 | х | х | х |
Продолжение таблицы 3 Расчетные данные для оценки гиперболической зависимости
| №п/п | х | у |  |  |  |  |
|---|---|---|---|---|---|---|
| 1 | 100 | 70 | 72,3262 | 0,033231 | 5,411206 | 519,1886 |
| 2 | 105 | 79 | 79,49405 | 0,006254 | 0,244083 | 190,0458 |
| 3 | 108 | 85 | 83,47619 | 0,017927 | 2,322012 | 60,61728 |
| 4 | 113 | 84 | 89,64321 | 0,067181 | 31,84585 | 77,1887 |
| 5 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 6 | 118 | 85 | 95,28761 | 0,121031 | 105,8349 | 60,61728 |
| 7 | 110 | 96 | 86,01027 | 0,10406 | 99,79465 | 10,33166 |
| 8 | 115 | 99 | 91,95987 | 0,071112 | 49,56344 | 38,6174 |
| 9 | 119 | 100 | 96,35957 | 0,036404 | 13,25272 | 52,04598 |
| 10 | 118 | 98 | 95,28761 | 0,027677 | 7,357059 | 27,18882 |
| 11 | 120 | 99 | 97,41367 | 0,016024 | 2,516453 | 38,6174 |
| 12 | 124 | 102 | 101,46 | 0,005294 | 0,291565 | 84,90314 |
| 13 | 129 | 105 | 106,1651 | 0,011096 | 1,357478 | 149,1889 |
| 14 | 132 | 112 | 108,8171 | 0,028419 | 10,1311 | 369,1889 |
| Итого: | 1629 | 1299 | 1298,988 | 0,666742 | 435,7575 | 1738,357 |
| Среднее значение: | 116,3571 | 92,78571 | х | х | х | х |
 | 8,4988 | 11,1431 | х | х | х | х |
 | 72,23 | 124,17 | х | х | х | х |
Значения параметров регрессии a и b составили:
Связь достаточно тесная.
В среднем расчётные значения отклоняются от фактических на 4,76%.
Таким образом, Н0 – гипотеза о случайной природе оцениваемых характеристик отклоняется и признаётся их статистическая значимость и надёжность.
Полученные оценки уравнения регрессии позволяют использовать его для прогноза. Если прогнозное значение индекса розничных цен на продукты питания х = 138, тогда прогнозное значение индекса промышленного производства составит:
По уравнению равносторонней гиперболы получена наибольшая оценка тесноты связи по сравнению с линейной и степенной регрессиями. Средняя ошибка аппроксимации остаётся на допустимом уровне.
Регрессионный анализ
Методы корреляционного анализа, позволяющего решать задачи определения тесноты и направления связи, существующей между изучаемыми величинами. Регрессионный анализ представляет собой следующий этап статистического анализа и позволяет предсказать значения случайной величины на основании значений одной или нескольких независимых случайных величин. Достижение этой цели оказывается возможным за счет определения вида аналитического выражения, описывающего связь зависимой случайной величины Y (которую в этом случае называют результативным признаком) с независимыми случайными величинами Х1 ,Х2 , . Хm (которые называют факторами).
Основной задачей регрессионного анализа является установление формы линии регрессии и изучение зависимости между переменными. Основной задачей корреляционного анализа — выявление связи между случайными переменными и оценка ее тесноты.
Форма связи результативного признака Y с факторами Х1 ,Х2 , . Хm называется уравнением регрессии. В зависимости от типа выбранного уравнения различают линейную и нелинейную регрессию (например, квадратичную, логарифмическую, экспоненциальную и т. д.).
Регрессия может быть парная (простая) и множественная, что определяется числом взаимосвязанных признаков. Если исследуется связь между двумя признаками (результативным и факторным), то регрессия называется парной (простой); к этому типу относится, например, исследование зависимости между продажами и затратами на рекламу. Если исследуется связь между тремя и более признаками, то регрессия называется множественной (многофакторной) — например, если исследуется связь между уровнем потребления, доходом, финансовым состоянием и размером семьи.
На этапе регрессионного анализа решаются следующие основные задачи.
1. Выбор общего вида уравнения регрессии и определение параметров регрессии.
2. Определение в регрессии степени взаимосвязи результативного признака и факторов, проверка общего качества уравнения регрессии.
3. Проверка статистической значимости каждого коэффициента уравнения регрессии и определение их доверительных интервалов.
Простая линейная регрессия
Выбор общего вида уравнения регрессии является важной задачей, поскольку форма связи выявляет механизм получения значений зависимой случайной переменной Y. Форма связи может быть линейной или нелинейной. Линейная связь описывается линейным уравнением. Уравнение простой линейной регрессии имеет вид:
График этой функции называется линией регрессии. Линия регрессии точнее всего отражает распределение экспериментальных значений на диаграмме рассеяния, а угол ее наклона характеризует степень зависимости между двумя переменными.
Параметры уравнения регрессии могут быть определены с помощью метода наименьших квадратов (именно этот метод и используется в Microsoft Excel). При определении параметров модели методом наименьших квадратов минимизируется сумма квадратов остатков.
Для нахождения оценок параметров b0 и b1 доставляющих минимум функции Qocm, вычисляются и приравниваются к нулю частные производные этой функции, откуда система нормальных уравнении принимает следующий вид:
После простых преобразований имеем:
Тогда коэффициент наклона прямой регрессии равен:
а свободный член регрессии:
Для свободного члена последнее равенство можно переписать следующим образом:
откуда 





Отсюда следует, что для определения линии регрессии достаточно знать лишь ее коэффициент наклона b1. Равенство для b1. можно упростить, если использовать найденное значение выборочного коэффициента корреляции г:
где 
Из последнего выражения для b1, ясно виден общий смысл коэффициента корреляции: чем меньше г, тем ближе линия регрессии к горизонтальному положению, т. е. тем ближе будут средние значения уi,- к состоянию неизменяемости.
Для анализа общего качества уравнения линейной регрессии используется обычно коэффициент детерминации R2, который получается посредством простого возведения в квадрат коэффициента корреляции. Коэффициент детерминации показывает, в какой мере изменчивость величины Y объясняется поведением величины X. Например, если коэффициент корреляции совокупных данных, относящихся к производственным затратам, равняется 0,8, то коэффициент детерминации R2 = 0,82 = 0,64 или 64%. Это значение говорит о том, что 64% вариации (изменчивости) недельных затрат объясняется количеством изделий, выпущенных за неделю. Остальная часть (36%) вариации общих затрат объясняется другими причинами.
Так как в большинстве случаев уравнение регрессии приходится строить на основе выборочных данных, то возникает вопрос об адекватности построения уравнения данным генеральной совокупности. Для этого проводится проверка статистической значимости коэффициента детерминации R2 на основе F-критерия Фишера:
где n — число наблюдений, a m — число факторов в уравнении регрессии.
В математической статистике доказывается, что если гипотеза Н0: R2 = 0 выполняется, то величина F имеет F-распределение с k = m и l=п-ш-1 степенями свободы, т. е.
Гипотеза Н0: R2 = 0 о незначимости коэффициента детерминации R2 отвергается, если FP > Fкр, а принимается альтернативная гипотеза — о значимости R2 .При значениях 
Возможна ситуация, когда часть вычисленных коэффициентов регрессии не обладает необходимой степенью значимости, т. е. значения данных коэффициентов будут меньше их стандартной ошибки. В этом случае такие коэффициенты должны быть исключены из уравнения регрессии. Поэтому проверка адекватности построенного уравнения регрессии наряду с проверкой значимости коэффициента детерминации R2 включает в себя также и проверку значимости каждого коэффициента регрессии.
Значимость коэффициентов регрессии проверяется с помощью t-критерия Стьюдента:

где 
В математической статистике доказывается, что если гипотеза 
1 степенями свободы, т. е.
Гипотеза Н0: Ь1 = 0 о незначимости коэффициента регрессии отвергается, если │tp│> │tкр│, а принимается альтернативная о значимости Ь1. Кроме того, зная значение tкр можно найти границы доверительных интервалов для коэффициентов регрессии.
Пусть имеется корреляционное поле производства пшеницы (обозначено точками на графике) для 50-ти сельхоз предприятий. Здесь Y-годовой сбор пшеницы, X-площади посевов.
Регрессионный анализ позволяет определить аналитическое выражение для уравнения линии регрессии оценить значимость коэффициентов этого уравнения.
Задача. На рис. 2 представлены данные о суточном объеме производства и количестве занятых работников для некоторой совокупности дней. По представленным данным необходимо определить параметры уравнения линейной регрессии и выполнить его анализ.
Для расчета параметров уравнения линейной регрессии и проверки его адекватности исследуемому процессу, Microsoft Excel располагает функцией Регрессия. Для вызова этой функций необходимо выбрать команду меню Сервис→Анализ данных (Tools→Data Analysis). На экране раскроется диалоговое окно Анализ данных (Data Analysis), в котором следует выбрать значение Regression, в результате чего на экране появится диалоговое окно Regression, представленное на рис. 1
В диалоговом окне Regression задаются следующие параметры.
1. В поле Input Y Range (Входные данные У) вводится диапазон ячеек, содержащих исходные данные по результативному признаку. Диапазон должен состоять из одного столбца.
2. В поле Input X Range (Входные данные X) вводится диапазон ячеек, содержащих исходные данные факторного признака. Максимальное число входных диапазонов (столбцов) равно 16.
3. Флажок опции Labels (Метки) устанавливается в том случае, если первая строка/столбец во входном диапазоне содержит заголовок. Если заголовок отсутствует, этот флажок следует сбросить. В последнем случае для данных выходного диапазона будут автоматически созданы стандартные названия.
4. Флажок опции Confidence Level (Уровень надежности) устанавливается в том случае, если в расположенное рядом с флажком поле необходимо ввести уровень надежности, отличный от уровня 95%, применяемого по умолчанию. Установленный в данном поле уровень надежности используется для проверки значимости коэффициента детерминации и коэффициентов регрессии. Если данный флажок опции сброшен, в таблице параметров уравнения регрессии генерируются две одинаковые пары столбцов для границ доверительных интервалов.
5. Флажок опции Константа — нуль (Constant is Zero) устанавливается в том случае, когда требуется, чтобы линия регрессии прошла через начало координат (т. е. Ь0 = 0).
6. Переключатель в группе Output options (Режимы вывода) может быть установлен в одно из трех положений, определяющих, где должны быть размещены результаты расчета: Output Range (Выходной интервал), New Worksheet Ply (Новый рабочий лист) или New Workbook (Новая рабочая книга).
7. Флажок опции Residuals (Остатки) устанавливается в том случае, если в диапазон ячеек с выходными данными требуется включить столбец остатков.
8. Флажок опции Standardized Residuals (Стандартизованные остатки) устанавливается в том случае, если в диапазон ячеек с выходными данными требуется включить столбец стандартизованных остатков.
9. Флажок опции Residual Plots (График остатков) должен быть установлен, если на рабочий лист требуется вывести точечные графики зависимости остатков от факторных признаков xt.
10. Флажок опции Line Fit Plots (График подбора) должен быть установлен, если на рабочий лист требуется вывести точечные графики зависимости теоретических результативных значений у от факторных признаков х.
11. Флажок опции Normal Probability Plots (График вероятности нормального распределения) должен быть установлен, если на рабочий лист требуется вывести точечный график зависимости наблюдаемых значений у от автоматически формируемых интервалов персентелей.
Результаты решения данной задачи с помощью функции Regression представлены на рисунках 3-7.
На рисунке 3 представлены результаты расчета регрессионной статистики. Эти результаты соответствуют следующим статистическим показателям:
• Множественный R — коэффициент корреляции R;
• R-квадрат — коэффициент детерминации R2 (квадрат коэффициента корреляции);
• Нормированный R — нормированное значение коэффициента корреляции; •Стандартная ошибка — стандартное отклонение для остатков;
• Наблюдения — это число исходных наблюдений.
На рисунке 4 представлены результаты дисперсионного анализа, которые используются для проверки значимости коэффициента детерминации R2.
Значения в столбцах на рисунке. 4 имеют следующую интерпретацию.
• Столбец df — это число степеней свободы. Для строки Регрессия число степеней свободы определяется количеством факторных признаков m, для строки Остаток — числом наблюдений n и количеством переменных в уравнении регрессии m+1: п -(m + 1), а для строки Итого — суммой степеней свободы для строк Регрессия и Остаток и, следовательно, равно п — 1.
• Столбец SS — это сумма квадратов отклонений. Для строки Регрессия значение определяется как сумма квадратов отклонений теоретических данных от среднего:
Для строки Остаток это сумма квадратов отклонений эмпирических данных от теоретических:
•Для строки Итого это сумма квадратов отклонений эмпирических данных от среднего:
• Столбец MS содержит значения дисперсии, которые рассчитываются по формуле:

Для строки Регрессия это факторная дисперсия
•Для строки Остаток это остаточная дисперсия
• Столбец F содержит расчетное значение F-критерия Фишера Fp вычисляемое по формуле:
• Столбец Значимость F содержит значение уровня значимости, соответствующее вычисленному значению Fр.
На рисунке 5 представлены полученные значения коэффициентов регрессии Ь1, и их статистические оценки.
Столбцы на рисунке 5 содержат следующие значения.
• Стандартная ошибка — стандартные ошибки коэффициентов Ь1 и и b0 .
Погрешность линейного коэффициента уравнения равная 7,44 и ошибка свободного члена равная 59,5 вполне приемлемы по отношению к величинам данных коэффициентов. уравнения 23 статистически велика, так как превосходит значение свободного члена. Поэтому ошибки не должны значительно влиять на эффективность описания входных данных полученным регрессионным уравнением.
• t-статистика — расчетные значения t-критерия, вычисляемые по формуле:

Чем больше отличается от нуля величина t-статистики, тем статистически лучше.
• Р-значение — значения уровней значимости, соответствующие вычисленным значениям tp . Оно характеризует насколько стандартную погрешность можно считать статистически значимой
• Нижние 95% и Верхние 95% — нижние и верхние границы доверительных интервалов для коэффициентов регрессии Ь1. и b0.
На рисунке 6 представлены теоретические значения 

Наконец, на рисунке 7 показаны вычисленные интервалы перцентилей и соответствующие им эмпирические значения у.

Перцентили — это характеристики набора данных, которые выражают ранги элементов в виде процентов от 0 до 100%, а не в виде чисел от 1 до n, таким образом, что наименьшему значению соответствует нулевой перцентиль, наибольшему — 100-й, медиане — 50-й и т. д.
Перцентили можно рассматривать как показатели, разбивающие наборы количественных и порядковых данных на определенные части. Например, 70-й перцентиль эффективности продаж может быть равен 60 
Под рангом (R) понимают номер (порядковое место) значения случайной величины в наборе данных
Переходя к анализу полученных расчетных данных, можно построить уравнение регрессии с вычисленными коэффициентами, которое будет выражать зависимость объема производства от количества работников.
Значение множественного коэффициента детерминации R2= 0,79 (рис. 10.3) показывает, что 79% общей вариации результативного признака объясняется вариацией факторного признака X. Значит, выбранный фактор существенно влияет на объем производства, что подтверждает правильность включения его в построенную модель.
Рассчитанный уровень значимости (показатель Значимость F на рисунке 4) 
Проверка значимости коэффициента детерминации R2 и коэффициентов регрессии Ь0 и b1, при факторном признаке подтверждает адекватность полученного уравнения.
http://ecson.ru/economics/econometrics/zadacha-1.postroenie-regressii-raschyot-korrelyatsii-oshibki-approximatsii-otsenka-znachimosti-i-prognoz.html
http://pandia.ru/text/78/208/79466.php