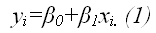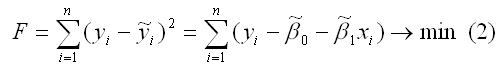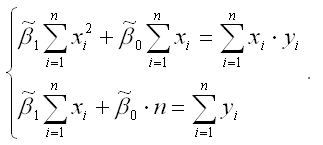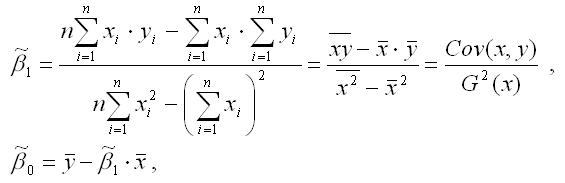Уравнение регрессии система нормальных уравнений

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 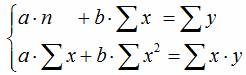. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

ML | Нормальное уравнение в линейной регрессии

Нормальное уравнение — это аналитический подход к линейной регрессии с функцией наименьших квадратов. Мы можем напрямую узнать значение θ без использования градиентного спуска . Следование этому подходу является эффективным и экономящим время вариантом при работе с набором данных с небольшими функциями.

Нормальное уравнение выглядит следующим образом:

В приведенном выше уравнении
θ: параметры гипотезы, которые определяют ее наилучшим образом.
X: введите значение функции каждого экземпляра.
Y: выходное значение каждого экземпляра.

Математика За уравнением —

Учитывая гипотезу функции

где,
N: нет. функций в наборе данных.
х ₀ : 1 (для векторного умножения)

Обратите внимание, что это скалярное произведение между значениями θ и x. Так что для удобства решения мы можем написать это как:

Мотивом в линейной регрессии является минимизация функции стоимости :

где,
x i : входное значение i ih учебного примера.
м: нет. учебных экземпляров
н: нет. функций набора данных
y i : ожидаемый результат i- го экземпляра

Представим функцию стоимости в векторной форме.

мы проигнорировали 1 / 2m здесь, поскольку это не будет иметь никакого значения в работе. Использовался для математического удобства при расчете градиентного спуска. Но это больше не нужно здесь.

х I _J: значение J функции Ih в я Ih примере обучения.

Это может быть дополнительно уменьшено до
Но каждая остаточная стоимость возводится в квадрат. Мы не можем просто возвести в квадрат вышеприведенное выражение. Так как квадрат вектора / матрицы не равен квадрату каждого из его значений. Таким образом, чтобы получить квадратное значение, умножьте вектор / матрицу на ее транспонирование. Итак, окончательное уравнение получено

Следовательно, функция стоимости

Итак, теперь получим значение θ, используя производную

Итак, это окончательно выведенное нормальное уравнение с θ, дающим минимальное значение стоимости.

Система нормальных уравнений и явный вид ее решения при оценивании методом наименьших квадратов линейной модели парной регрессии

Предположим, что в ходе регрессионного анализа была установлена линейная взаимосвязь между исследуемыми переменными х и у, которая описывается моделью регрессии вида:

В результате оценивания данной эконометрической модели определяются оценки неизвестных коэффициентов. Классический подход к оцениванию параметров линейной регрессии основан на методе наименьших квадратов (МНК).

Метод наименьших квадратов позволяет получить такие оценки параметров β₀и β₁, при которых сумма квадратов отклонений фактических значений результативного признака y от расчетных (теоретических) y˜ минимальна:

В процессе минимизации функции (1) неизвестными являются только значения коэффициентов β₀ и β₁, потому что значения результативной и факторной переменных известны из наблюдений. Для определения минимума функции двух переменных вычисляются частные производные этой функции по каждому из оцениваемых параметров и приравниваются к нулю. Результатом данной процедуры будет стационарная система уравнений для функции (2):

.

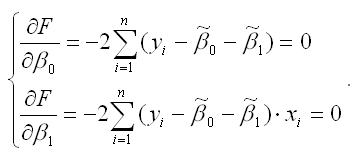
Если разделить обе части каждого уравнения системы на (-2), раскрыть скобки и привести подобные члены, то получим систему нормальных уравнений для функции регрессии вида yi=β₀+β₁xi:

Если решить данную систему нормальных уравнений, то мы получим искомые оценки неизвестных коэффициентов модели регрессии β₀ и β₁:

y – среднее значение зависимой переменной;

x – среднее значение независимой переменной;

xy – среднее арифметическое значение произведения зависимой и независимой переменных;

G 2 (x) – дисперсия независимой переменной;

Gcov (x, y) – ковариация между зависимой и независимой переменными.

Таким образом, явный вид решения системы нормальных уравнений может быть записан следующим образом: