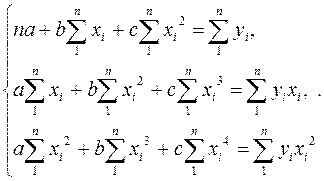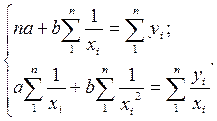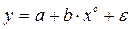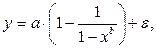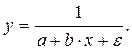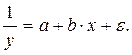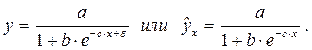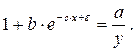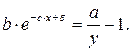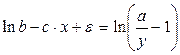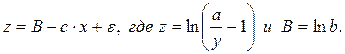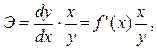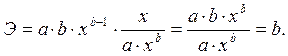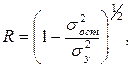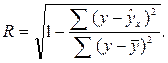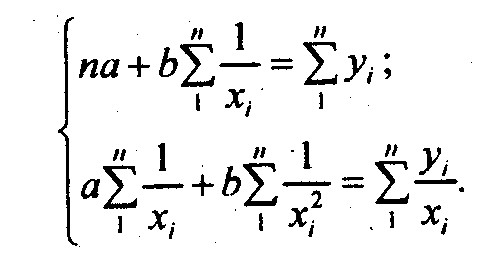Уравнение нелинейной регрессии
Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии
Виды нелинейной регрессии
| Вид | Класс нелинейных моделей |
| Нелинейные относительно включенных в анализ объясняющих переменных, но линейные по оцениваемым параметрам |
| Нелинейные по оцениваемым параметрам |
Здесь ε — случайная ошибка (отклонение, возмущение), отражающая влияние всех неучтенных факторов.
Уравнению регрессии первого порядка — это уравнение парной линейной регрессии.
Уравнение регрессии второго порядка это полиномальное уравнение регрессии второго порядка: y = a + bx + cx 2 .
Уравнение регрессии третьего порядка соответственно полиномальное уравнение регрессии третьего порядка: y = a + bx + cx 2 + dx 3 .
Чтобы привести нелинейные зависимости к линейной используют методы линеаризации (см. метод выравнивания):
- Замена переменных.
- Логарифмирование обеих частей уравнения.
- Комбинированный.
| y = f(x) | Преобразование | Метод линеаризации |
| y = b x a | Y = ln(y); X = ln(x) | Логарифмирование |
| y = b e ax | Y = ln(y); X = x | Комбинированный |
| y = 1/(ax+b) | Y = 1/y; X = x | Замена переменных |
| y = x/(ax+b) | Y = x/y; X = x | Замена переменных. Пример |
| y = aln(x)+b | Y = y; X = ln(x) | Комбинированный |
| y = a + bx + cx 2 | x1 = x; x2 = x 2 | Замена переменных |
| y = a + bx + cx 2 + dx 3 | x1 = x; x2 = x 2 ; x3 = x 3 | Замена переменных |
| y = a + b/x | x1 = 1/x | Замена переменных |
| y = a + sqrt(x)b | x1 = sqrt(x) | Замена переменных |
Пример . По данным, взятым из соответствующей таблицы, выполнить следующие действия:
- Построить поле корреляции и сформулировать гипотезу о форме связи.
- Рассчитать параметры уравнений линейной, степенной, экспоненциальной, полулогарифмической, обратной, гиперболической парной регрессии.
- Оценить тесноту связи с помощью показателей корреляции и детерминации.
- Дать с помощью среднего (общего) коэффициента эластичности сравнительную оценку силы связи фактора с результатом.
- Оценить с помощью средней ошибки аппроксимации качество уравнений.
- Оценить с помощью F-критерия Фишера статистическую надежность результатов регрессионного моделирования. По значениям характеристик, рассчитанных в пп. 4, 5 и данном пункте, выбрать лучшее уравнение регрессии и дать его обоснование.
- Рассчитать прогнозное значение результата, если прогнозное значение фактора увеличится на 15% от его среднего уровня. Определить доверительный интервал прогноза для уровня значимости α=0,05 .
- Оценить полученные результаты, выводы оформить в аналитической записке.
| Год | Фактическое конечное потребление домашних хозяйств (в текущих ценах), млрд. руб. (1995 г. — трлн. руб.), y | Среднедушевые денежные доходы населения (в месяц), руб. (1995 г. — тыс. руб.), х |
| 1995 | 872 | 515,9 |
| 2000 | 3813 | 2281,1 |
| 2001 | 5014 | 3062 |
| 2002 | 6400 | 3947,2 |
| 2003 | 7708 | 5170,4 |
| 2004 | 9848 | 6410,3 |
| 2005 | 12455 | 8111,9 |
| 2006 | 15284 | 10196 |
| 2007 | 18928 | 12602,7 |
| 2008 | 23695 | 14940,6 |
| 2009 | 25151 | 16856,9 |
Решение. В калькуляторе последовательно выбираем виды нелинейной регрессии. Получим таблицу следующего вида.
Экспоненциальное уравнение регрессии имеет вид y = a e bx
После линеаризации получим: ln(y) = ln(a) + bx
Получаем эмпирические коэффициенты регрессии: b = 0.000162, a = 7.8132
Уравнение регрессии: y = e 7.81321500 e 0.000162x = 2473.06858e 0.000162x
Степенное уравнение регрессии имеет вид y = a x b
После линеаризации получим: ln(y) = ln(a) + b ln(x)
Эмпирические коэффициенты регрессии: b = 0.9626, a = 0.7714
Уравнение регрессии: y = e 0.77143204 x 0.9626 = 2.16286x 0.9626
Гиперболическое уравнение регрессии имеет вид y = b/x + a + ε
После линеаризации получим: y=bx + a
Эмпирические коэффициенты регрессии: b = 21089190.1984, a = 4585.5706
Эмпирическое уравнение регрессии: y = 21089190.1984 / x + 4585.5706
Логарифмическое уравнение регрессии имеет вид y = b ln(x) + a + ε
Эмпирические коэффициенты регрессии: b = 7142.4505, a = -49694.9535
Уравнение регрессии: y = 7142.4505 ln(x) — 49694.9535
Особенности построения модели нелинейной регрессии. Индекс корреляции
Линейные связи являются основными. Однако встречаются и нелинейные связи, хорошо описываемые параболой, гиперболой, степенной функцией и т. д.
Уравнение регрессии в форме параболы 2-го порядка имеет следующий вид:
Если при линейной связи среднее изменение результативного признака на единицу фактора постоянно по всей области вариации фактора, то при параболической корреляции изменение признака х на единицу признака у меняется равномерно с изменением величины фактора. В результате связь может даже поменять знак на противоположный, из прямой превратится в обратную, из обратной в прямую. Такой характер связи объективно присущ многим системам.
Например, с увеличением дозы удобрений урожайность сельхозкультур сначала повышается, но если превысить оптимальную величину дозы, то при дальнейшем росте дозы удобрений растения угнетаются и урожайность снижается.
Нормальные уравнения метода наименьших квадратов для параболы 2-го порядка таковы:
Решая эту систему, получаем значения параметров a, b и с.
Уравнение регрессии в форме гиперболы имеет следующий вид:

Если величина b положительна, то при увеличении значений факторного признака х значения результативного признака уменьшаются, причем это уменьшение все время замедляется, и при х → ∞ средняя величина признака у будет равна а. Если же параметр b отрицателен, то значения результативного признака с ростом фактора возрастают, причем их рост замедляется, и в пределе при х → ∞ у=а. Таким образом, гиперболические зависимости характерны для связей, в которых результативный признак не может варьировать неограниченно, его вариация имеет односторонний предел. Например, при освоении нового оборудования его производительность возрастет, но рост замедлится по мере приближения к конструктивно-технологическому пределу производственной мощности агрегата. Совершенствуя двигатель, можно увеличивать его КПД, но тоже не выше предела, допускаемого данным видом преобразования энергии. Таков же характер связи между уровнем душевого дохода х в семье и долей семей, имеющих домашние кинотеатры, у; он приближен к пределу (100%) в наиболее обеспеченной группе семей.
Нормальные уравнения метода наименьших квадратов для гиперболы таковы:
Легко видеть, что эти уравнения, по существу, те же, что и для линейной связи. Линеаризация гиперболического уравнения достигается заменой 1/х на новую переменную, которую можно обозначить z. Тогда уравнение гиперболы примет вид у = а + b∙z.
По-другому обстоит дело с регрессией, нелинейной по оцениваемым параметрам. Данный класс нелинейных моделей подразделяется на два типа: нелинейные модели внутренне линейные и нелинейные модели внутренне нелинейные. Если нелинейная модель внутренне линейна, то она с помощью соответствующих преобразований может быть приведена к линейному виду. Если же нелинейная модель внутренне нелинейна, то она не может быть сведена к линейной функции. Например, в эконометрических исследованиях при изучении эластичности спроса от цен широко используется степенная функция:
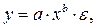
где у – спрашиваемое количество;
ε — случайная ошибка.
Данная модель нелинейна относительно оцениваемых параметров, т.к. включает параметры а и b неаддитивно. Но ее можно считать внутренне линейной, ибо путем логарифмирования данного уравнения по основанию е оно преобразовывается к линейному виду:
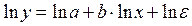
Соответственно оценки параметров а и b могут быть найдены МНК. В рассматриваемой степенной функции предполагается, что случайная ошибка ε мультипликативно связана с объясняющей переменной х. Если же модель представить в виде 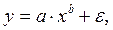
Внутренне нелинейной будет и модель вида
ибо эти уравнения не могут быть преобразованы в уравнения, линейные по коэффициентам.
В специальных исследованиях по регрессионному анализу часто к нелинейным относят модели, только внутренне нелинейные по оцениваемым параметрам, а все другие модели, которые внешне нелинейны, но путем преобразований параметров могут быть приведены к линейному виду, относятся к классу линейных моделей. В этом плане к линейным относят, например, экспоненциальную модель 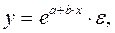
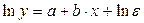
Если модель внутренне нелинейна по параметрам, то для оценки параметров используются итеративные процедуры, успешность которых зависит от вида уравнений и особенностей применяемого итеративного подхода. Модели внутренне нелинейные по параметрам могут иметь место в эконометрических исследованиях. Однако, гораздо большее распространение получили модели, приводимые к линейном виду. Решение такого типа моделей реализовано в стандартных пакетах прикладных программ. Среди них, в частности, можно назвать и обратную модель вида
Обращая обе части равенства, получим линейную форму модели для переменной 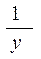
Приводима к линейному виду и логистическая функция
Обращая обе части равенства, получим:
Вычитая 1, имеем
Прологарифмировав обе части по натуральному основанию, получим уравнение линейной формы:
Среди нелинейных функций, которые могут быть приведены к линейному виду, в эконометрических исследованиях очень широко используется степенная функция 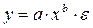
Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя под действием единичного относительного изменения экономического фактора, от которого он зависит при неизменных остальных влияющих на него факторах.
Эластичностью функции y=f(x) называется предел отношения относительных изменений переменных y и x:
где 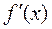
Для степенной функции она составит: 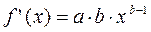
Это означает, что величина коэффициента b показывает, на сколько процентов изменится в среднем результат, если фактор изменится на 1%.
Коэффициент эластичности, естественно, можно определять и при наличии других форм связи, но только для степенной функции он представляет собой постоянную величину, равную параметру b. В других функциях коэффициент эластичности зависит от значений фактора х.
Уравнение нелинейной регрессии, так же как и в линейной зависимости, дополняется показателем корреляции, а именно индексом корреляции (R):
где 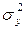
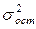
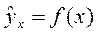
Так как 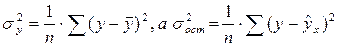
Величина данного показателя находится в границах: 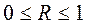
Поскольку в расчете индекса корреляции используется соотношение факторной и общей суммы квадратов отклонений, то R 2 имеет тот же смысл, что и коэффициент детерминации. В специальных исследованиях величину R 2 для нелинейных связей называют индексом детерминации.
Оценка существенности индекса корреляции проводится, так же как и оценка надежности коэффициента корреляции.
8.10. Гиперболическая корреляция
Уравнение регрессии в форме гиперболы имеет следующий вид :
Если величина Ъ положительна , то при увеличении значений факторного признака х значения результативного признака уменьшаются , причем это уменьшение все время замедляется , и при х -> оо средняя величина признака у будет равна а . Если же параметр Ь отрицателен , то значения результативного признака с ростом фактора возрастают , причем — их рост замедляется , и в пределе при х → ∞ у? = а . Таким образом , гиперболические зависимости характерны для связей , в которых результативный признак не может варьировать неограниченно , его вариация имеет односторонний предел . Например , при освоении нового оборудования его производительность возрастет , но рост замедлится по мере приближения к конструктивно — технологическому пределу производственной мощности агрегата . Совершенствуя двигатель , можно увеличивать его КПД , но тоже не выше предела , допускаемого данным видом преобразования энергии . Таков же характер связи между уровнем душевого дохода х в семье и долей семей , имеющих телевизоры , у ; он приближен к пределу (100%) в наиболее обеспеченной группе семей . Нормальные уравнения метода наименьших квадратов для гиперболы таковы :
Легко видеть , что эти уравнения , по существу , те же , что и для линейной связи . Линеаризация гиперболического уравнения достигается заменой 1/ х на новую переменную , которую можно обозначить z. Тогда уравнение (8.27) примет вид y ? = а + bz. Это и следует c делать , вычисляя гиперболу на компьютере , если программа для него не предусматривает автоматического вычисления гиперболических регрессий .
В качестве примера расчета уравнения гиперболической связи рассмотрим влияние среднесуточного прироста живой массы крупного рогатого скота на откорме на себестоимость прироста живой массы в совокупности предприятий области , занимавшихся откормом скота ( табл . 8.6).
где х в сотнях граммов
Гиперболическая связь себестоимости прироста со
скоростью прироста массы скота
Группы предприятий по среднесуточному приросту массы граммов на 1 голову х i
http://mydocx.ru/4-12749.html
http://www.stathelp.ru/ots/g8p10.html