Уравнение регрессии в квадратическом виде

Уравнение регрессии

Вместе с этим калькулятором также используют следующие:
Уравнение множественной регрессии

В сервисе для нахождения параметров регрессии используется МНК. Система нормальных уравнений для линейной регрессии: 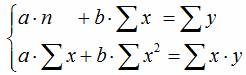. Также можно получить ответ, используя матричный метод. см. также Статистические функции в Excel

Уравнение парной регрессии относится к уравнению регрессии первого порядка. Если эконометрическая модель содержит только одну объясняющую переменную, то она имеет название парной регрессии. Уравнение регрессии второго порядка и уравнение регрессии третьего порядка относятся к нелинейным уравнениям регрессии.

Пример . Осуществите выбор зависимой (объясняемой) и объясняющей переменной для построения парной регрессионной модели. Дайте графическое изображение регрессионной зависимости. Определите теоретическое уравнение парной регрессии. Оцените адекватность построенной модели (интерпретируйте R-квадрат, показатели t-статистики, F-статистики).
Решение будем проводить на основе процесса эконометрического моделирования.
1-й этап (постановочный) – определение конечных целей моделирования, набора участвующих в модели факторов и показателей, их роли.
Спецификация модели — определение цели исследования и выбор экономических переменных модели.
Ситуационная (практическая) задача. По 10 предприятиям региона изучается зависимость выработки продукции на одного работника y (тыс. руб.) от удельного веса рабочих высокой квалификации в общей численности рабочих x (в %).
2-й этап (априорный) – предмодельный анализ экономической сущности изучаемого явления, формирование и формализация априорной информации и исходных допущений, в частности относящейся к природе и генезису исходных статистических данных и случайных остаточных составляющих в виде ряда гипотез.
Уже на этом этапе можно говорить о явной зависимости уровня квалификации рабочего и его выработкой, ведь чем опытней работник, тем выше его производительность. Но как эту зависимость оценить?
Парная регрессия представляет собой регрессию между двумя переменными – y и x , т. е. модель вида:

29. Линейная регрессия

Рассмотрим двумерную случайную величину (X, Y), где X и Y – зависимые случайные величины.

Представим приближенно одну случайную величину как функцию другой. Точное соответствие невозможно. Будем считать, что эта функция линейная.

Для определения этой функции остается только найти постоянные величины a и b.

Определение. Функция G(X) называется Наилучшим приближением случайной величины Y в смысле метода наименьших квадратов, если математическое ожидание

принимает наименьшее возможное значение. Также функция G(X) называется Среднеквадратической регрессией Y на X.

Теорема. Линейная средняя квадратическая регрессия Y На Х вычисляется по формуле:

В этой формуле Mx=M(X), My=M(Y), коэффициент корреляции величин Х И Y.

Величина называется Коэффициентом регрессии Y На Х.

Прямая, уравнение которой

,

Называется Прямой сренеквадратической регрессии Y На Х.

Величина называется Остаточной дисперсией Случайной величины Y относительно случайной величины Х. Эта величина характеризует величину ошибки, образующейся при замене случайной величины Y линейной функцией G(X)=aХ + B.

Видно, что если R=±1, то остаточная дисперсия равна нулю, и, следовательно, ошибка равна нулю и случайная величина Y точно представляется линейной функцией от случайной величины Х.

Прямая среднеквадратичной регрессии Х на Y определяется аналогично по формуле:

Прямые среднеквадратичной регрессии пересекаются в точке (Тх, ту), которую называют Центром совместного распределения Случайных величин Х И Y.

Статистика — Квадратичное уравнение регрессии

Квадратичная регрессия применяется для определения уравнения параболы, которое может наилучшим образом соответствовать заданному набору данных. Это имеет следующую форму:

y = a x 2 + b x + c w h e r e a n e 0

y = a x 2 + b x + c w h e r e a n e 0

Метод наименьших квадратов можно использовать для определения уравнения квадратичной регрессии. В этом методе мы находим значения a, b и c таким образом, чтобы квадрат вертикального расстояния между каждой данной точкой ( x i , y i ) и уравнением параболы ( y = a x 2 + b x + 2 ) минимально. Матричное уравнение для параболической кривой имеет вид:

Коэффициент корреляции, г

Коэффициент корреляции r определяет, насколько хорошо квадратное уравнение может соответствовать заданным данным. Если r близко к 1, то это хорошо подходит. r можно вычислить по следующей формуле.

r = 1 − f r a c S S E S S T г д е [ 7 p t ] S S E = s u m ( y i − a x i 2 − b x + i − c ) 2 [ 7 p t ] S S T = s u m ( y i − b a r y ) 2

r = 1 − f r a c S S E S S T г д е [ 7 p t ] S S E = s u m ( y i − a x i 2 − b x + i − c ) 2 [ 7 p t ] S S T = s u m ( y i − b a r y ) 2