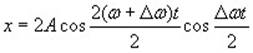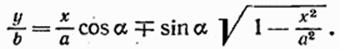Уравнение результирующего колебания при биениях

Амплитуда биения. Сложение взаимно перпендикулярных колебаний

Векторная диаграмма.

Векторная диаграмма — графическое изображение меняющихся по закону синуса (косинуса) величин и соотношений между ними при помощи направленных отрезков — векторов. Векторные диаграммы широко применяются в электротехнике, акустике, оптике, теории колебаний и так далее.

Гармоническое (то есть синусоидальное) колебание может быть представлено графически в виде проекции на некоторую ось (обычно берут ось координат Оx) вектора, вращающегося с постоянной угловой скоростью ω. Длина вектора соответствует амплитуде, угол поворота относительно оси (Ox) — фазе.

Сумма (или разность) двух и более колебаний на векторной диаграмме представлена при этом (геометрической) суммой [1] (или разностью) векторов этих колебаний. Мгновенное значение искомой величины определяется при этом проекцией вектора суммы на ось Оx, амплитуда — длиной этого вектора, а фаза — углом его поворота относительно Ox.

Сложение нескольких гармонических колебаний одного направления.

Сложение гармонических колебаний одного направления и одинаковой частоты. Биения

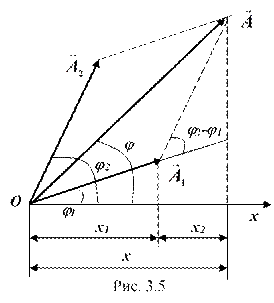
Пусть совершаются два гармонических колебания одного направления и одинаковой частоты

(4.1)

Уравнение результирующего колебания будет иметь вид

Убедимся в этом, сложив уравнения системы (4.1)

Применив теорему косинусов суммы и сделав алгебраические преобразования:

(4.2)

Можно найти такие величины А и φ0 , чтобы удовлетворялись уравнения

(4.3)

Рассматривая (4.3) как два уравнения с двумя неизвестными А и φ0, найдем, возведя их в квадрат и сложив, а затем разделив второе на первое:

Подставляя (4.3) в (4.2), получим:

Или окончательно, используя теорему косинусов суммы, имеем:

Тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ2-φ1) сгладываемых колебаний.

В зависимости от разности фаз (φ2-φ1):

1) (φ2-φ1) = ±2mπ (m=0, 1, 2, …), тогда A= А1+А2, т. е. амплитуда результирующего колебания А равна сумме амплитуд складываемых колебаний;

2) (φ2-φ1) = ±(2m+1)π (m=0, 1, 2, …), тогда A= |А1-А2|, т. е. амплитуда результирующего колебания равна разности амплитуд складываемых колебаний

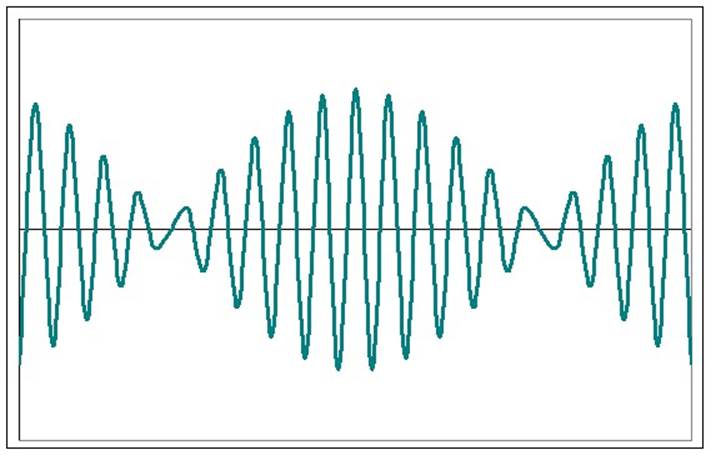
Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биением.

Пусть два колебания мало отличаются по частоте. Тогда амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω намного меньше ω. Начало отсчета выберем так, чтобы начальные фазы обоих колебаний были равны нулю:

Результирующее колебание можно рассматривать как гармоническое с частотой ω, амплитуда А, которого изменяется по следующему периодическому закону:

Частота изменения А в два раза больше частоты изменения косинуса. Частота биений равна разности частот складываемых колебаний: ωб = Δω

Биения, Период биения.

Бие́ния — явление, возникающее при наложении двух периодических колебаний, например, гармонических, близких по частоте, выражающееся в периодическом уменьшении и увеличении амплитуды суммарного сигнала.Частота изменения амплитуды суммарного сигнала равна разности частот исходных сигналов.

Период биений Т_б — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π.

Амплитуда биения. Сложение взаимно перпендикулярных колебаний.

Допустим, что материальная точка может совершать колебания как вдоль оси х, так и вдоль перпендикулярной к ней оси у. Если возбудить оба колебания, материальная точка будет двигаться по некоторой, вообще говоря, криволинейной траектории, форма которой зависит от разности фаз обоих колебаний.

Выберем начало отсчета времени так, чтобы начальная фаза первого колебания была равна нулю. Тогда уравнения колебаний запишутся следующим образом:

где — разность фаз обоих колебаний.

Выражения (57.1) представляют собой заданное в параметрической форме уравнение траектории, по которой движется тело, участвующее в обоих колебаниях. Чтобы получить уравнение траектории в обычном виде, нужно исключить из уравнений (57.1) параметр t. Из первого уравнения следует, что

Теперь развернем косинус во втором из уравнений (57.1) по формуле для косинуса суммы, подставляя при этом вместо их значения (57.2) и (57.3). В результате получим

Последнее уравнение после несложных преобразований можно привести к виду

Последнее уравнение есть, вообще говоря, уравнение эллипса, оси которого повернуты относительно координатных осей х и у. Ориентация эллипса и величина его полуосей зависят довольно сложным образом от амплитуд а и b и разности фаз

Определим форму траектории для некоторых частных случаев.

1. Разность фаз а равна нулю. В этом случае уравнение (57.4) принимает вид

откуда получается уравнение прямой

Результирующее движение является гармоническим колебанием вдоль этой прямой с частотой и амплитудой, равной (рис. 57.1).

2. Разность фаз а равна Уравнение (57.4) имеет вид

откуда получается, что результирующее движение представляет собой гармоническое колебание вдоль прямой (рис. 57.2)

3. При уравнение (57.4) переходит в

т. е. в уравнение эллипса, приведенного к координатным осям, причем полуоси эллипса равны соответствующим амплитудам колебаний.

При равенстве амплитуд а и эллипс вырождается в окружность.

Случаи отличаются направлением движения по эллипсу или по окружности. Если уравнения (57.1) можно записать следующим образом:

В момент тело находится в точке (рис. 57.3). В последующие моменты времени координата х уменьшается, а координата у становится отрицательной. Следовательно, движение совершается по часовой стрелке.

При уравнения колебаний имеют вид

Отсюда можно заключить, что движение происходит против часовой стрелки.

Из сказанного следует, что равномерное движение по окружности радиуса R с угловой скоростью со может быть представлено как сумма двух взаимно перпендикулярных колебаний:

(57.10)

(знак «+» в выражении для у соответствует движению против часовой стрелки, знак «—» — движению по часовой стрелке).

В случае, когда частоты взаимно перпендикулярных колебаний отличаются на очень малую величину их можно рассматривать как колебания одинаковой частоты, но с медленно изменяющейся разностью фаз. В самом деле, уравнения колебаний можно представить следующим образом:

и выражение рассматривать как разность фаз, медленно изменяющуюся со временем по линейному закону.

Результирующее движение в этом случае происходит по медленно видоизменяющейся кривой, которая будет последовательно принимать форму, отвечающую всем значениям разности фаз от до

Если частоты взаимно перпендикулярных колебаний не одинаковы, то траектория результирующего движения имеет вид довольно сложных кривых, называемых фигурами Лиссажу. На рис. 57.4 показана одна из простейших траекторий, получающаяся при отношении частот 1 : 2 и разности фаз Уравнения колебаний имеют вид

За то время, пока вдоль оси х точка успевает переместиться из одного крайнего положения в другое, вдоль оси у, выйдя из нулевого положения, она успевает достигнуть одного крайнего положения, затем другого и вернуться в нулевое положение.

При отношении частот 1:2 и разности фаз, равной нулю, траектория вырождается в незамкнутую кривую (рис. 57.5), по которой точка движется туда и обратно.

Чем ближе к единице рациональная дробь, выражающая отношение частот колебаний, тем сложнее оказывается фигура Лиссажу. На рис. 57.6 для примера показана кривая для отношения частот 3 : 4 и разности фаз .

Электронная библиотека

Колеблющееся тело может одновременно участвовать в нескольких колебательных процессах:

Сложение гармонических колебаний одного направления и одинаковой частоты производится методом вращающегося вектора амплитуды.

Векторные диаграммы этих колебаний изображены на рис. 3.5. Так как векторы и вращаются с одинаковой угловой скоростью w₀, то разность фаз (j_{1 –} j₂) между ними остается постоянной. Уравнение результирующего колебания будет иметь вид:

где амплитуда результирующего колебания определяется по формуле: ; начальная фаза результирующего колебания равна: .

Таким образом, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (j_{2 –} j₁) складываемых колебаний:

Для практики особый интерес представляет случай, когда два складываемых колебания одинакового направления мало отличаются по частоте.

В результате сложения этих колебаний получаются колебания с периодически изменяющейся амплиту дой – биения.

Уравнения двух колебаний с амплитудами А и близкими частотами w и w + Dw, причем Dw Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00

Частота биений, формула

Период биений

Период биений Т_б — это промежуток между соседними моментами времени, в которые амплитуда обращается в нуль, а фаза изменяется на π .

Поскольку при аргументе, равном π /2, 3 π /2 …, косинус обращается в нуль, имеем:

Решая это уравнение относительно частоты биений, получаем

Частота биений

Частота биений есть отношение числа минимумов амплитуды ко времени. Частота биений определяется как разность частот составляющих колебаний.

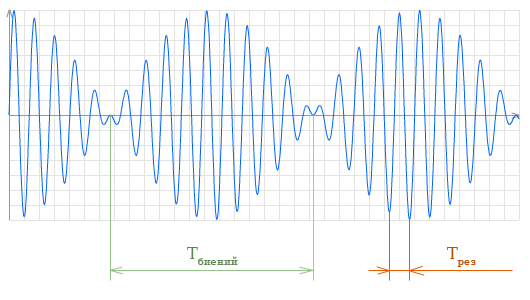
Частота результирующих колебаний получается из формулы результирующего отклонения биений [2]

Отсюда находим период результирующих колебаний Т_рез = 1/f_рез