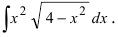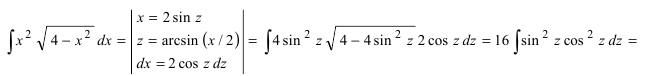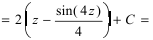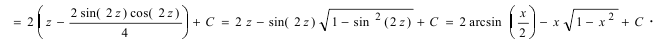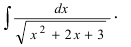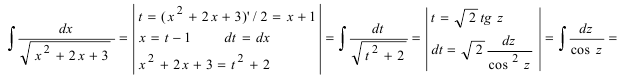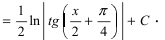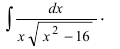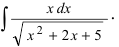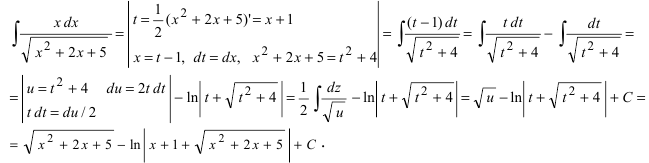Интегрирование иррациональных функций: способы и примеры решений
Будут и задачи для самостоятельного решения, к которым можно посмотреть ответы.
Рассмотрим интегралы от иррациональных функций, то есть функций, содержащих переменную (обычно икс) под корнем или, что то же самое — в дробной степени. Интегралы от таких функций с помощью подстановок приводятся к интегралам от рациональных функций и могут быть проинтегрированы окончательно.
В подынтегральном выражении — различные дробно-рациональные функции
Разберём интегралы, где в подынтегральном выражении переменная присутствует под корнем. В формально обобщённом виде речь идёт об интегралах вида

В примерах мы увидим, что переменная икс, присутствующая под корнем, присутствует там без степени. В примере 3 икс присутствует также в квадрате, но при этом — не по корнем. То есть корни отдельно, степени — отдельно.
В этом случае важное значение имеет наименьшее общее кратное чисел λ , . μ (или общий знаменатель, если эти числа дробные). Обозначим это наименьшее общее кратное (общий знаменатель) через n . Рассматриваемые интегралы от иррациональных функций можно найти, используя следующую подстановку:
Тогда каждая дробная степень «икса» выразится через целую степень «тэ» и подынтегральная функция преобразуется в рациональную функцию от «тэ».
Пример 1. Найти интеграл от иррациональной функции 
Решение. Преобразуем все корни икса в степени. Выписываем степени при иксе в подынтегральном выражении — все, которые там находим:

Находим наименьшее общее кратное знаменателей этих чисел: 4.
Поэтому используем следующую подстановку:
Подставляем и преобразуем:
Возвращаясь к переменной икс, окончательно находим:

Пример 2. Найти интеграл от иррациональной функции 
Решение. Используем следующую подстановку:
Подставляем и преобразуем:
Интегрируем и получаем:
Возвращаясь к переменной икс, окончательно находим:

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 3. Найти интеграл от иррациональной функции 
Пример 4. Найти интеграл от иррациональной функции

Корень из квадратного трёхчлена и подстановки Эйлера
Если дан интеграл иррациональной функции вида

то есть в подынтегральном выражении — корень из квадратного трёхлчена, то можно воспользоваться подстановками Эйлера.

В зависимости от характера корней квадратного уравнения используются следующие подстановки Эйлера.
1. Если x 1 , x 2 — действительные числа (не комплексные), то используется подстановка
(первая подстановка Эйлера).
2. Если x 1 , x 2 — комплексные числа и a > 0 , то используется подстановка
(вторая подстановка Эйлера).
3. Если x 1 , x 2 — комплексные числа и c > 0 , то используется подстановка
(третья подстановка Эйлера).
Пример 5. Найти интеграл от иррациональной функции 
Решение. Разложим квадратный трёхчлен на множители:
Используем первую подстановку Эйлера:
Интегрируем и получаем:
Возвращаясь к переменной икс, сначала долго занимаемся преобразованием выражений, а затем окончательно находим:
Пример 6. Найти интеграл от иррациональной функции 
Используем вторую подстановку Эйлера:
Интегрируем и получаем:

Возвращаясь к переменной икс, окончательно находим:

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 7. Найти интеграл от иррациональной функции 
(использовать третью подстановку Эйлера).
Интегралы от дифференциального бинома и подстановки Чебышева

где m, n, p — рациональные числа (целые или дробные), называются интегралами от дифференциального бинома. В примерах мы увидим, что в подынтегральных выражениях переменная икс присутствует не только под корнем: она под корнем, но ещё и в степени. В этом главное отличие рассматриваемых интегралов от тех, которые были рассмотрены в первом параграфе.
Чтобы найти такие интегралы, используются подстановки Чебышева.
1. Если p — целое число, то используется подстановка

где k — наименьшее общее кратное знаменателей m и n.
2. Если 

где s — знаменатель дроби p .
3. Если 

где s — знаменатель дроби p .
Русский математик П.Л. Чебышев доказал, что только в перечисленных трёх случаях интеграл от дифференциальных биномов с рациональными показателями степени выражается через элементарные функции.
Пример 8. Найти интеграл от иррациональной функции 
Преобразуем корни в степени и избавимся от дроби:
Здесь p = -1 (целое число). Чтобы избавиться от степени икса в скобках, сделаем промежуточную подстановку


Теперь сделаем следующую подстановку:
Подставляем и получаем:
Возвращаемся к переменной z :

Возвращаясь к переменной икс, окончательно находим:

Пример 9. Найти интеграл от иррациональной функции 
Преобразуем корни в степени и избавимся от дроби:

Здесь m = 3 , n = 2 , 

Cделаем промежуточную подстановку


Теперь, чтобы избавиться от дробной степени выражения в скобках, сделаем следующую подстановку:

Интегрируем и получаем:

Возвращаемся к переменной z :

Возвращаясь к переменной икс, окончательно находим:

Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 10. Найти интеграл от иррациональной функции 

Частный случай квадратичных иррациональностей
Рассмотрим интеграл от иррациональной функции вида

где в знаменателе — квадратный корень из квадратного трёхчлена.
Чтобы проинтегрировать любой интеграл такого вида, необходимо уметь находить интегралы 

Формула для нахождения первого из них:

Второй интеграл находится по формуле

Формулы (2 и (3) можно условно считать табличными интегралами. Если в подкоренном выражении интеграла (1) выделить полный квадрат, то при a > 0 это выражение примет вид
После подстановки t = x – m в первом случае интеграл (1) приводится к интегралу (3), во втором – к интегралу (2).
Пример 11. Найти интеграл от иррациональной функции
Решение. Выделим в подкоренном выражении полный квадрат:
Произведя теперь подстановку
причём при интегрировании воспользовались формулой (3). Возвращаясь к старой переменной, окончательно получим
Найти интеграл от иррациональной функции самостоятельно, а затем посмотреть решение
Пример 12. Найти интеграл от иррациональной функции
Уравнение с интегралами квадратными корнями
Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!
Контакты
 |
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Прямоугольная система координат на плоскости и ее применение
- Линии второго порядка
- Полярные координаты
- Непрерывность функции
- Формула Тейлора и ее применение
- Интегрирование рациональных дробей
- Интегрирование тригонометрических функций
- Интегрирование тригонометрических выражений
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
http://yukhym.com/ru/integrirovanie-funktsii/integraly-ot-funktsij-kvadratnoe-uravnenie-v-znamenatele.html
http://www.evkova.org/integrirovanie-irratsionalnyih-funktsij





























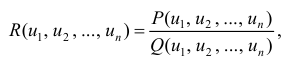
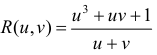 — рациональная функция переменных u и v, при этом:
— рациональная функция переменных u и v, при этом: 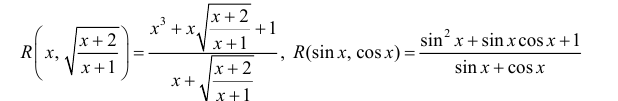

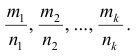 Тогда подстановка
Тогда подстановка 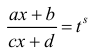
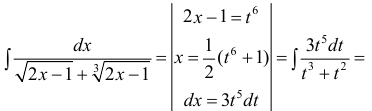
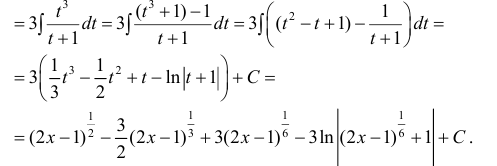
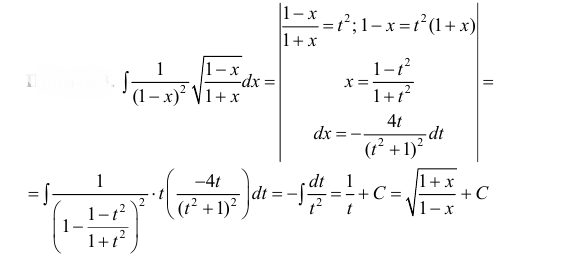
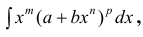
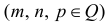 — интегралы от дифференциального бинома.
— интегралы от дифференциального бинома. 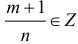 , тогда подстановка
, тогда подстановка 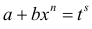 , где s – знаменатель р приводит интегральную функцию к рациональной.
, где s – знаменатель р приводит интегральную функцию к рациональной. 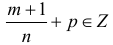 , тогда подстановка
, тогда подстановка 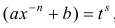 , где s – знаменатель р приводит интегральную функцию к рациональной.
, где s – знаменатель р приводит интегральную функцию к рациональной. 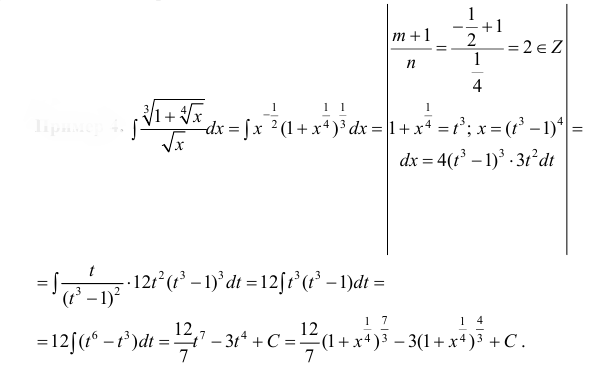
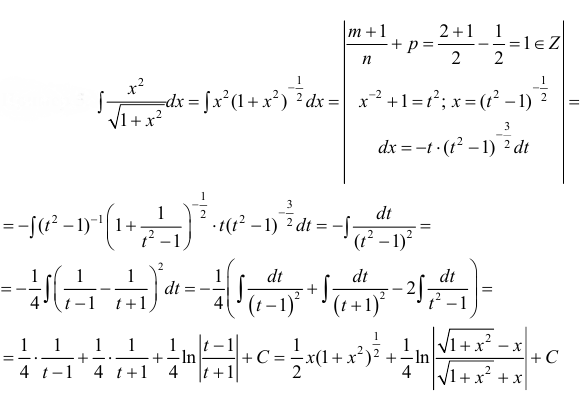
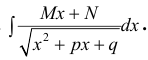 Вычисление интегралов проводится аналогично интегралам
Вычисление интегралов проводится аналогично интегралам 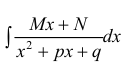 выделением полного квадрата в трехчлене
выделением полного квадрата в трехчлене 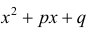 (см. § 21, примеры 1, 2).
(см. § 21, примеры 1, 2).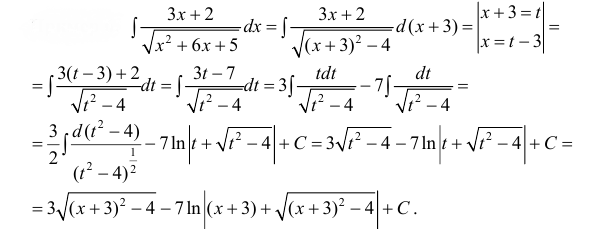
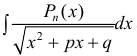 , где
, где 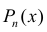 — многочлен степени n.
— многочлен степени n. 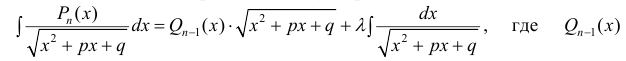 многочлен степени n−1 . Коэффициенты многочлена
многочлен степени n−1 . Коэффициенты многочлена 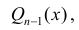 а также число λ находятся, если продифференцировать правую и левую часть равенства (2).
а также число λ находятся, если продифференцировать правую и левую часть равенства (2).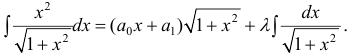 После взятия производной:
После взятия производной: 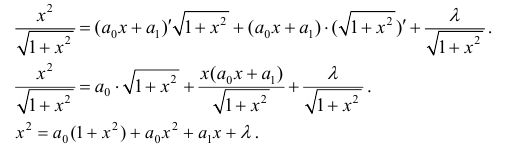

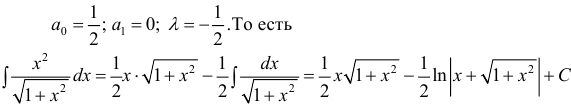
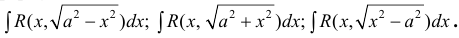
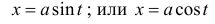 — для первого интеграла,
— для первого интеграла, 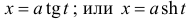 — для второго,
— для второго, 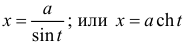 — для третьего (см. § 23).
— для третьего (см. § 23).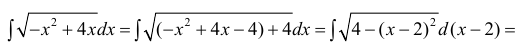
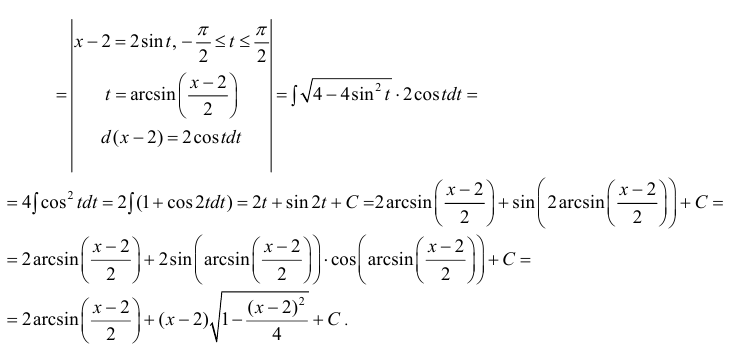

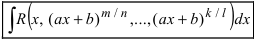 .
.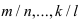 находят наименьший общий знаменатель, который обозначим через р;
находят наименьший общий знаменатель, который обозначим через р;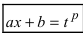 .
.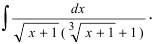
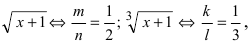 следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.
следовательно, наименьший общий знаменатель этих дробей равен 6. Таким образом.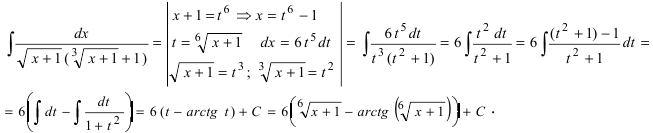
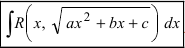 .
.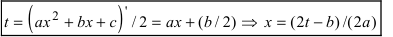 приводятся к одному из интегралов вида:
приводятся к одному из интегралов вида: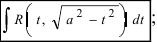 2.
2. 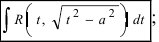 3.
3.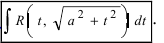
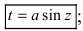 2.
2. 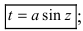 3.
3. 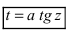 — которые позволяют избавиться от квадратного корня.
— которые позволяют избавиться от квадратного корня.