Графический метод при решении иррациональных уравнений
Продолжаем изучать методы решения иррациональных уравнений. Сейчас сосредоточимся на графическом методе. Сначала скажем, в каких ситуациях для решения иррациональных уравнений применяется графический метод. Дальше кратко напомним основные положения метода, его особенности и алгоритм. После этого подробно разберем решения наиболее характерных иррациональных уравнений.
Какие иррациональные уравнения решаются графически
Обычно, графическим методом решаются иррациональные уравнения, для которых выполняются два следующих условия:
- Не видно другого более простого метода решения.
- Функции, отвечающие частям уравнения, довольно простые в плане построения графиков.
Понятно, что в общем случае построение графиков функций – это дело непростое. Именно поэтому графическим методом решают лишь уравнения f(x)=g(x) , которые, во-первых, не решаются другим способом или решение другим способом сопряжено со значительными сложностями, и, во-вторых, для которых функции f и g либо основные элементарные, либо их графики могут быть получены из графиков основных элементарных функций при помощи геометрических преобразований.
Например, решать графическим методом иррациональное уравнение 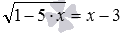
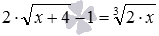
Краткое описание метода, его особенности и алгоритм
Подробное описание графического метода дано в статье «Графический метод решения уравнений». Здесь мы не будем повторяться, а лишь кратко и без пояснений напомним главные положения этого метода, его особенности и алгоритм.
Графический метод решения уравнений предполагает использование графиков функций, отвечающих частям уравнения, для нахождения решения уравнения. Корнями уравнения являются абсциссы точек пересечения графиков функций.
Без использования специализированных компьютерных программ сложно достичь высокой точности построения графиков функций. Поэтому, все результаты, полученные с использованием графиков, мы можем считать лишь приближенными, нуждающимися в проверке и обосновании (кроме, разве что, самых очевидных). Это главная особенность графического метода.
Наконец, алгоритм. Согласно графическому методу решения уравнений, нужно:
- Построить в одной прямоугольной системе координат графики функций, отвечающие левой и правой частям уравнения.
- По чертежу определить все точки пересечения графиков:
- если точек пересечения нет, то решаемое уравнение не имеет корней,
- если точки пересечения имеются, то переходим к следующему шагу алгоритма.
- По чертежу определить абсциссы всех точек пересечения графиков – это приближенные значения всех корней исходного уравнения.
- Если есть основания полагать, что некоторые или все определенные на предыдущем шаге значения являются точными значениями корней решаемого уравнения, то осуществить их проверку, например, подстановкой.
Решение характерных иррациональных уравнений
Практическую часть откроем иррациональным уравнением, для решения которого непросто предложить какой-либо аналитический метод. А вот графический метод позволяет показать, что уравнение не имеет корней.
Решите иррациональное уравнение
Иногда графический метод позволяет определить точные значения корней уравнения. Это обычно происходит, когда корнями являются целые числа. Но даже целые корни, найденные по графикам, полезно проверять при помощи подстановки в исходное уравнение. Продемонстрируем это при решении следующего иррационального уравнения графическим методом.
Решить уравнение
Часто при помощи графического метода невозможно получить точные значения корней. Более того, в некоторых случаях по графикам невозможно определить даже количество корней уравнения, не то что их значения. Это касается тех случаев, когда графики функций, отвечающие правой и левой части уравнения, очень близки на некоторых участках, почти совпадают. Выход из такой ситуации может состоять в построении графиков именно на этих участках в увеличенном масштабе при повышенной точности построения. Однако делать это без компьютера проблематично, и по понятным причинам предпочтительнее обратиться к какому-либо аналитическому методу решения, если, конечно, есть такая возможность.
Решить иррациональное уравнение
Мы подробно рассмотрели как графический метод применяется при решении иррациональных уравнений. Можно приступать к изучению следующего метода решения иррациональных уравнений — метода, базирующегося на свойствах возрастающих и убывающих функций.
Урок-практикум «Графическое решение уравнений, содержащих функцию y=√х (функцию квадратного корня)». 8-й класс
Разделы: Математика
Класс: 8
Базовый учебник: Алгебра 8 класс. Учебник для общеобразовательных учреждений/ А. Г. Мордкович.
Цель урока: применить алгоритм решения уравнений графически к функции у = 
Задачи:
- Обучающая: способствовать закреплению знаний свойств функции у =
, умение строить график этой функции, использовать алгоритм графического решения уравнений применительно к графику квадратного корня из неотрицательного числа.
- Развивающая: развитие умения правильно оперировать полученными знаниями, логически мыслить; развитие инициативы, умения принимать решения, не останавливаться на достигнутом; работа на интерактивной доске, познавательная активность.
- Воспитывающая: воспитание познавательного интереса к предмету; к самостоятельности при решении учебных задач; воспитание воли и упорства для достижения конечных результатов.
Тип урока: урок практикум.
Методы:
- словестные: фронтальная работа
- наглядные алгоритм, графики.
- практические: индивидуальная, парная и групповая работа, тренировочная самостоятельная работа.
Оборудование: учебник, рабочая тетрадь, раздаточный материал, школьная доска, интерактивная доска.
План урока.
1. Организационный момент. 1 мин
2. Проверка домашнего задания. 5 мин
3. Актуализация знаний. Устная работа с классом. 7 мин
4. Закрепление материала 20 мин
5. Тренировочная самостоятельная работа. 8 мин
6. Постановка домашнего задания. 3 мин
7. Рефлексия. 1 мин
8. Итог урока. 1мин
Ход урока
1. Организационный момент.
2. Проверка домашнего задания. (Учащиеся проверяют домашнюю работу, сверяясь с эталоном, оценивают правильность и полноту выполнения согласно критериям, ставят оценку).
Для №13.3 Сопоставьте график который получился у вас дома с одним из графиков. Слайд 2. Из данных утверждений (приложение 1 у каждого ученика) выберите те свойства, которые подходят для функции у = — 
С помощью графика найдите: Слайд 3
а) значения у при х = 1; 
б) значения х, если у = 0; -2; -4; (выборочно)
в) наименьшее и наибольшее значения функции на отрезке 
г) при каких значениях х график функции расположен выше прямой у = -2. Ниже прямой у = -2.
3. Актуализация знаний. Устная работа с классом.
1. Принадлежит ли графику функции у = 
А(2; 
2. Найдите наименьшее и наибольшее значение функции у = 
а) на отрезке 
б) на полуинтервале [4; 7);
в) на луче [0; 
3. Решите уравнение по заданному графику: х 2 = х +2. Слайд 6
Учащиеся вспоминают (7 класс) алгоритм решения уравнений данного типа, проговаривая, что является корнем уравнения. Как данное задание мы будем применять на уроке.
Ученики говорят тему урока(на доске записана), формулируют цель,
4. Закрепление материала
Задание 1. Итак, повторив алгоритм решения уравнений графически выполним задание № 13.9 (б).
(ученик у доски, остальные в тетради)

1) Рассмотрим две функции у = 
2) Построим график функции у = 
х 0 1 4 у 0 1 2
3) Построим график функции у = 6 – х,
х 0 2 у 6 4
4) По графику устанавливаем, что графики пересекаются в одной точке А(4; 2). Проверим принадлежность данной точки нашим функциям.
Ответ: х = 4. Слайд 7
Задание 2 Решить уравнение графически: два человека у доски остальные на местах выполняют соответственно свои варианты самостоятельно. Совместно устраняют в ходе проверки обнаруженные пробелы (на доске и на листах учеников готовая памятка с построенным графиком линейной функции). Построение графика квадратного корня 
Памятка 1 вариант
а) – 
| х | 0 | 1 |
| у | -2 | -1 |
Оцените себя, отметив уровень этого показателя. Понимание: – ______________+
Памятка 2 вариант
б) — 
| х | 0 | 1 |
| у | 2 | -1 |
Оцените себя, отметив уровень этого показателя. Понимание: – ______________+
Задание 3. Решить графически систему уравнений
(работа выполняется в парах используя приложение № 2)
После выполнения задания учащиеся проверяют свое решение, сравнивая с эталоном. Слайд 8
Встаньте те кто справился с данным заданием.
Физкультминутка для глаз. Слайд 9
Задание 4. Работа в группах(задания дифференцированы, приложение 3): Слайд 10
Задание 1 группе: Докажите, что графики функций у = 
Чтобы доказать, что графики функций y = 
Задание 2 группе: Сколько корней имеет данное уравнение 
а) Построим график функции y = 
Таким образом, очевидно, что уравнение 
Задание 3 группе: Сколько корней имеет данное уравнение 
Прямые вида y = –x + b – это параллельные прямые, которые образуют тупой угол с положительным направлением оси абсцисс.
Получаем, что уравнение 
Обсуждение решений каждой группы.( Для готовых графиков квадратного корня на интерактивной доске учащиеся показывают свои решения)
5. Тренировочная самостоятельная работа.
В а р и а н т 1
1 . По графику функции у = 
а) значение функции при х = 3, у =____
б) значение аргумента, которому соответствует значение y = 1,8; х = _____
2. Принадлежит ли графику функции y = 
а) А (36; 6); ______ б) В (–9; 3)_______?
3. Решите уравнение графически — 
На листочках с самостоятельной работой поставьте:
1 – если на уроке вам было интересно и понятно;
2 – интересно, но не понятно;
3 – не интересно, но понятно;
4 – не интересно, не понятно.
В а р и а н т 2
1. По графику функции y = 
а) значение функции при х = 5; у =
б) значение аргумента, которому соответствует значение у = 1,5; х =
2. Принадлежит ли графику функции y = — 
а) А (81; -9)______ б) В (–16; 4)_______
3. Решите уравнение графически 
На листочках с самостоятельной работой поставьте:
1 – если на уроке вам было интересно и понятно;
2 – интересно, но не понятно;
3 – не интересно, но понятно;
4 – не интересно, не понятно.
Проверяем работу с помощью эталона. Слайд 13 Выясняем проблемы по данной теме.
6. Постановка домашнего задания.
№ 13.9(г), № 13.11(г), № 13.16(рис 7 опишите свойства функции)
7. Рефлексия.
На листочках с самостоятельной работой поставьте:
1 – если на уроке вам было интересно и понятно;
2 – интересно, но не понятно;
3 – не интересно, но понятно;
4 – не интересно, не понятно.
8. Итог урока.
Урок я хочу закончить словами древнегреческого ученого Фалеса:
Что быстрее всего? – Ум
Что мудрее всего? – Время
Что приятнее всего? Достичь желаемого.
Я думаю, мы с вами достигли желаемого? Еще раз вспомнли функцию квадратного корня из неотрицательного числа и применили алгоритм решения уравнения графически к этой функции. Но ребята, кроме у = 



Так что перспектива развития ваших знаний велика. Дерзайте.
Приложение № 1
Для номера 13.3 Сопоставьте график который получился у вас дома с одним из графиков. Слайд 2
Из данных утверждений выберите те свойства, которые подходят для функции у = — 
- Область определения функции – луч [0; +
)
- Область определения функции – луч ( +
; 0]
- у = 0 при х = 0, у 0
- Функция убывает на луче [0; +
)
- Функция возрастает на луче [0; +
)
- унаиб = 0, унаим не существует
- Функция непрерывна на луче [0; +
)
- Область значения функции – луч [0; +
)
- Область значения функции – луч (-
; 0]
- Функция выпукла вниз.
- Функция выпукла вверх.
Приложение 2
Работа в парах Задание № 3
Решите графически систему уравнений:
Приложение 3
Работа в группах Задание № 4
Задание 1 группе: Докажите, что графики функций у = 
Задание 2 группе: Сколько корней имеет данное уравнение 
Задание 3 группе: Сколько корней имеет данное уравнение 
Графический способ отделения корней
Отделение корней
Постановка задачи
Решение уравнений с одной переменной
Рассмотрим уравнение вида F(x)=0, где F(x) – определенная и непрерывная на отрезке [a,b] функция.
Корнем уравнения F(x)=0 называется такое значение x * , которое обращает уравнение в верное равенство.
x * – корень уравнения F(x)=0 x * – нуль функции y=F(x).
Решить уравнение – значит установить, имеет ли оно корни, сколько корней, и найти их значения с заданной степенью точности.
Нахождение корней уравнения состоит из двух этапов:
I. Отделение корней – выделение промежутков, содержащих ровно 1 корень.
II. Уточнение корней – нахождение корней с заданной степенью точности.
Отделение корней может осуществляться графически или программным путем.
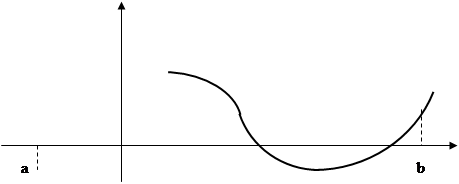
Искомые промежутки: [-1; 0] [1; 2].
б) Иногда проще рассмотреть вместо уравнения y=F(x) равносильное ему уравнение f1(x)=f2(x). В этом случае требуется указать отрезок, содержащий абсциссу точки пересечения графиков функций y=f1(x) и y=f2(x).
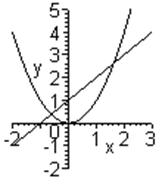
Искомые промежутки: [-2; 0] [1; 3].
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Студент – человек, постоянно откладывающий неизбежность. 10577 – 

78.85.5.224 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
 |
По этому методу производят построение и последующий визуальный анализ графиков y = P(x) и y = Q(x) или графика 



Точки пересечения графиков y = P(x) и y = Q(x) или графика 
Учет кратности корня имеет большое значение не только для определения общего числа корней уравнения, но и для последующего процесса уточнения корня. В частности, некоторые методы уточнения эффективны только для простых корней, а при уточнении корней четной кратности приходится решать вспомогательное уравнение 


После построения графиков функций P(x) и Q(x) или 
Аналитический метод отделения корней
Применяется для отделения корней нечетной кратности уравнения вида 




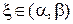

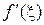
Процесс отделения корней начинается с установления знаков функции 

Затем определяются знаки функции 


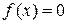

Наиболее просто отделение корней производится с помощью ЭВМ. Алгоритм отделения корня уравнения 

Алгоритм отделения наименьшего корня предполагает выполнение следующих этапов (рис. 3):
1. Задается шаг Δx отделения корня (блок 2).
2. Переменной x задается значение нижней границы отрезка [a, b], и вычисляется значение y1 функции 
3. Вычисляется значение переменной x в следующей точке, отстоящей от предыдущей точки на шаг Δx отделения корня. Определяется значение y2 функции 
4. Проверяется условие существования корня в текущем интервале длиной, равной шагу Δx отделения корня (блок 6).
5. Если знак функции 



6. Если знак функции 
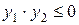
7. Если на исследуемом интервале [a, b] требуется отделить все корни уравнения 

Контрольные вопросы и упражнения для приобретения
Умений и навыков по теме 2
1. В каком виде могут быть записаны уравнения с одним неизвестным? На какие классы разделяются нелинейные уравнения с одним неизвестным?
2. Что значит термин «решить уравнение»? Что называют решением уравнения, а что – корнем уравнения?
3. Сколько корней имеет алгебраическое уравнение вида 
4. Привести к виду 

5. Что означает утверждение «корень вычислен с заданной степенью точности»?
6. Как определяется область существования корней алгебраического уравнения? Определите области существования положительных и отрицательных корней алгебраического уравнения 
7. Какова методика определения области корней трансцендентного уравнения? Определите область существования корней уравнения
8. Какие подзадачи содержит в себе общая задача нахождения приближенного значения корня уравнения? Что значит «отделить корни уравнения»? Какие методы применяют для отделения корней уравнения?
9. Используя два способа, т. е. записывая нижеприведенное уравнение в виде 


10. Какая теорема лежит в основе аналитического метода отделения корней уравнения? При каком условии отделенный на интервале (α, β) корень ξ является единственным?
11. Напишите в вербальной (словесной) форме последовательность отделения наибольшего корня уравнения 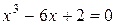
[1] Дробно-рациональная функция содержит выражение, где переменная x является делителем или входит в состав делителя.
[2] Выполнение условия 
Дата добавления: 2019-01-14 ; просмотров: 161 ; ЗАКАЗАТЬ РАБОТУ
Пусть дано уравнение вида (2.1), 
Процесс численного решения уравнения разбивается на два этапа: отделение корней и уточнение корней.
Определение 2.2. Говорят, что корень Е, уравнения вида (2.1) или (2.2) отделен на данном промежутке, если он содержится в этом промежутке и других корней на том же промежутке нет.
Определение 2.3. Произвести полное отделение всех корней уравнения — значит разбить всю область допустимых значений на промежутки, в каждом из которых содержится только один корень или не содержится ни одного корня.
Для проверки существования корня уравнения на данном интервале применяют некоторые теоремы о свойствах непрерывных функций. Приведем некоторые из них.
Теорема 2.3 (первая теорема Больцано — Коши). Если функция/(х) непрерывна на отрезке [а; Ь] и принимает на концах отрезка значения разных знаков, то внутри отрезка [а; Ъ] существует, по крайней мере, один корень уравнения Дх) = 0.
Рис. 2.5. К теореме 2.3
Заметим, что при выполнении условий теоремы 2.3 на отрезке [а; Ь] не следует, что на данном отрезке существует один или несколько корней (рис. 2.5). Важно иметь признак, по которому можно судить о наличии на отрезке [а; b] только одного корня. Этот признак выражается следующей теоремой (рис. 2.6).
Теорема 2.4. Если функция /(х) непрерывна и монотонна на отрезке [а; Ь] и принимает на концах отрезка значения разных знаков, то внутри отрезка [а; Ь] существует корень уравнения /(х) = 0, и притом единственный.
Рис. 2.6. К теореме 2.4
Вопрос о том, является ли функция монотонной, можно решить как элементарными методами, так и с помощью понятия производной, а именно: если функция Дх) непрерывна на отрезке [а; ?>] и имеет производную fix) внутри отрезка, то при fix) > 0 функция Дх) возрастает, а при/'(х) h(b), тогда внутри отрезка [а; Ь] существует корень уравнения g(x) = hix), и притом единственный.
Рис. 2.7. К теореме 2.6
Отделение корней лучше всего произвести графически. Для этого необходимо построить либо графики функций g(x) и h(x) для уравнения вида(2.1), либо график функцииДх) для уравнения вида (2.2). Построив соответствующие графики, можно сделать предположение о том, в каких интервалах находятся корни уравнения. Это предположение затем следует проверить аналитически, применяя одну из теорем 2.3—2.6.
Отделите корни уравнения х 3 – бх 2 + 20 = 0.
Построим график функцииу(х) = х 3 – бх 2 -I- 20 (рис. 2.8).
Рис. 2.8. Г рафик функции у(х) =х 3 – бх 2 + 20
На основе рис. 2.8 можно сделать предположение, что в каждом из отрезков [-2; -1], [2; 3], [5; 6] имеется по одному корню данного уравнения. Проверим это предположение для отрезка [2; 3]. На концах отрезка функция принимает значения
т.е. значения разных знаков. Производная
для всех х из интервала (2; 3), т.е. имеет постоянный знак. Следовательно, в силу теоремы 2.4 внутри отрезка [2; 3] уравнение х 3 – бх 2 + 20 = 0 имеет единственный корень.
Подобными рассуждениями можно доказать, что внутри каждого отрезка [-2; -1] и [5; 6] имеется по одному корню, в чем предлагаем убедиться читателю самостоятельно.
http://urok.1sept.ru/articles/659649
http://dudom.ru/kompjutery/graficheskij-sposob-otdelenija-kornej/
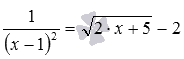
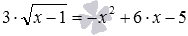









 )
)








