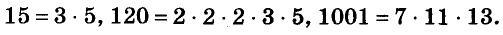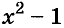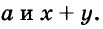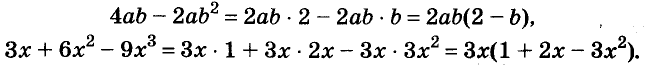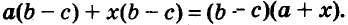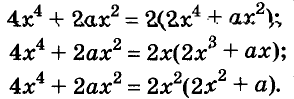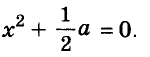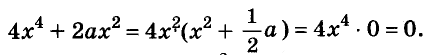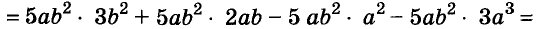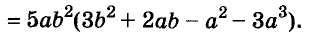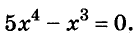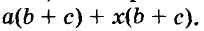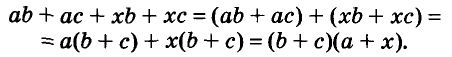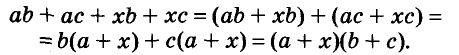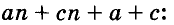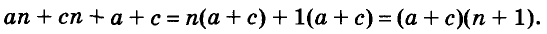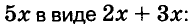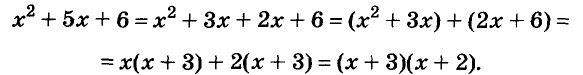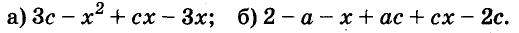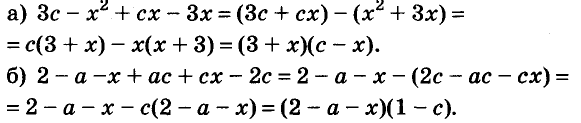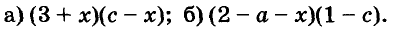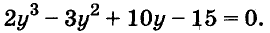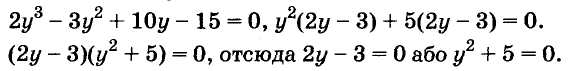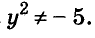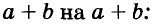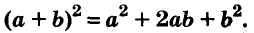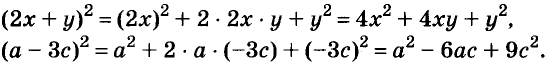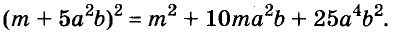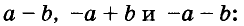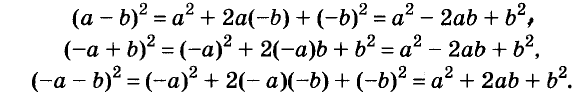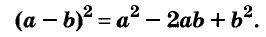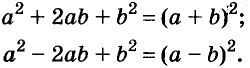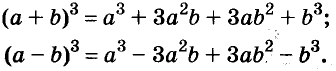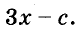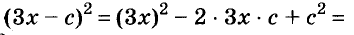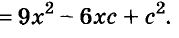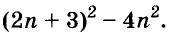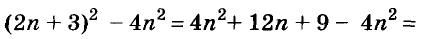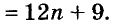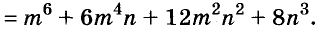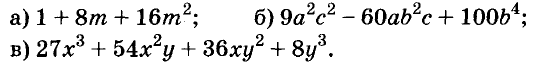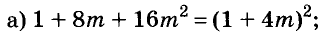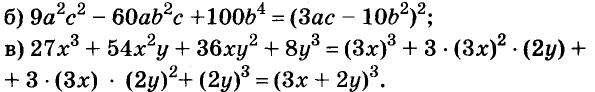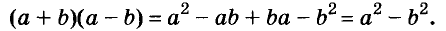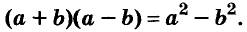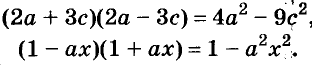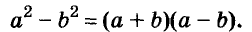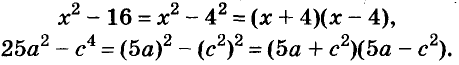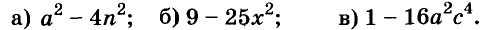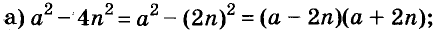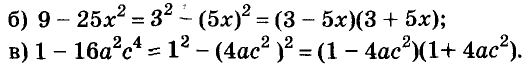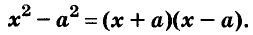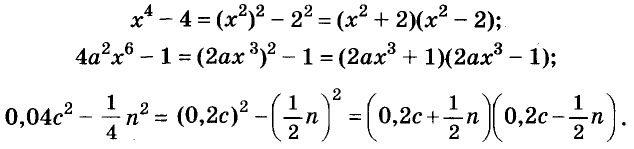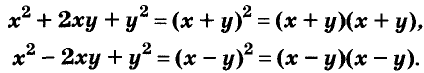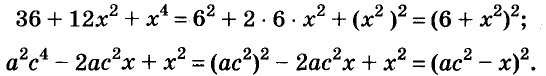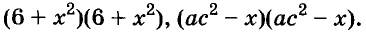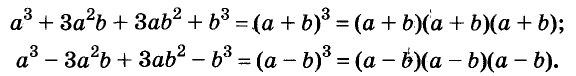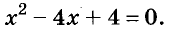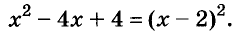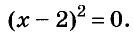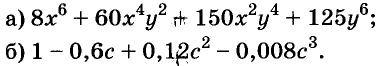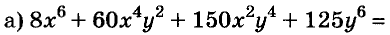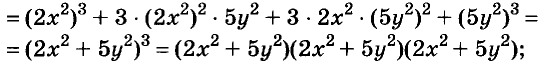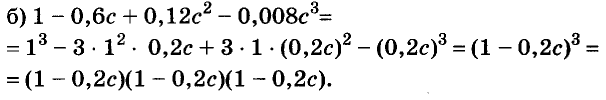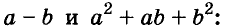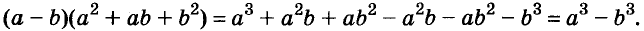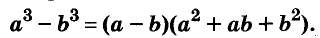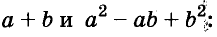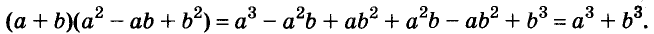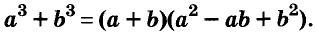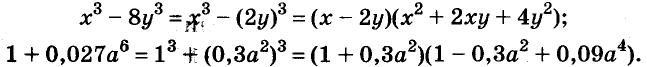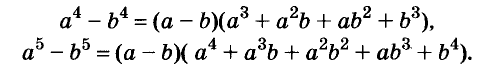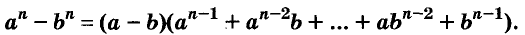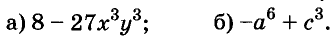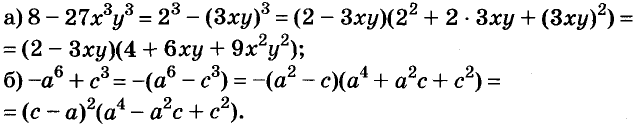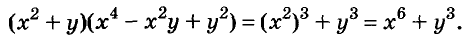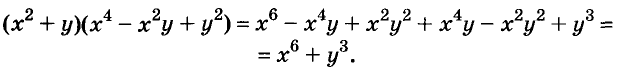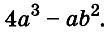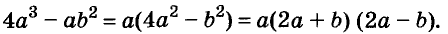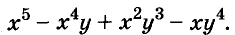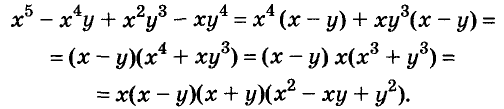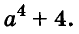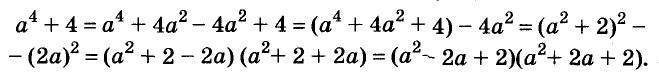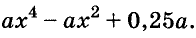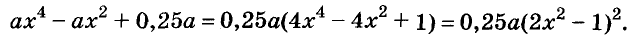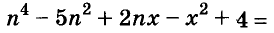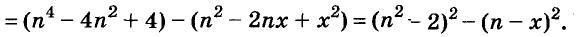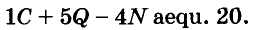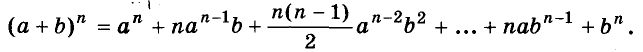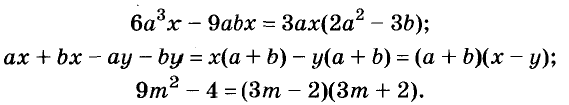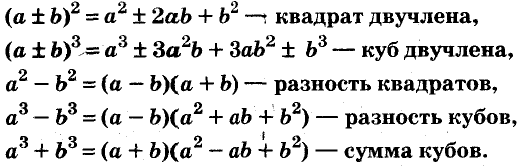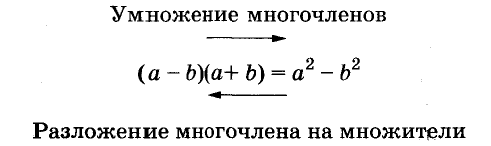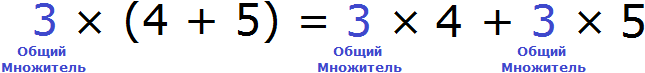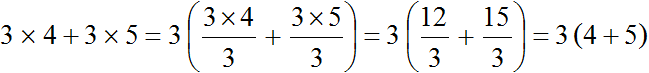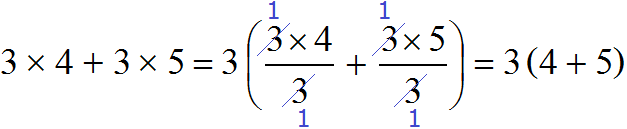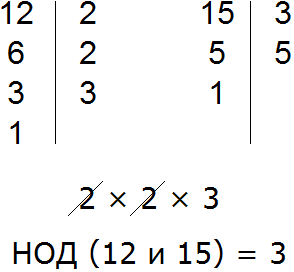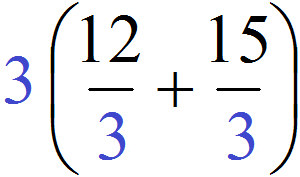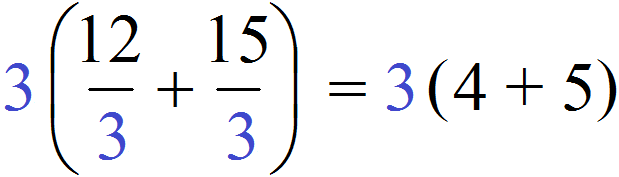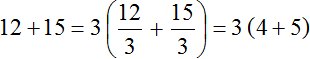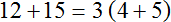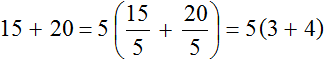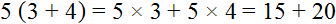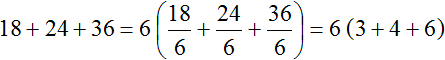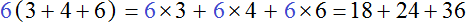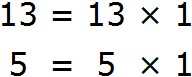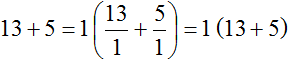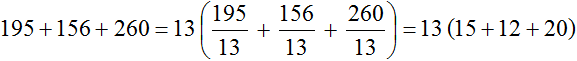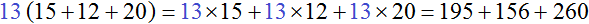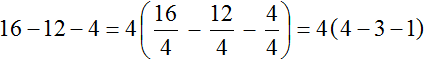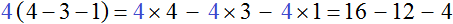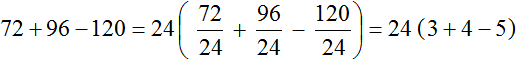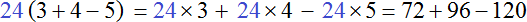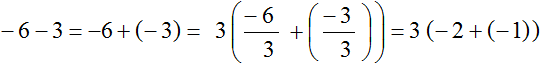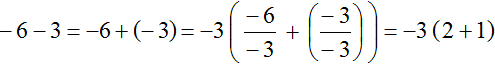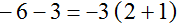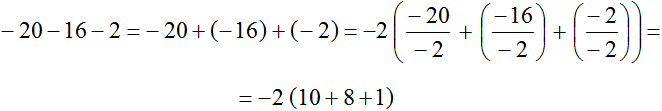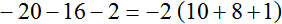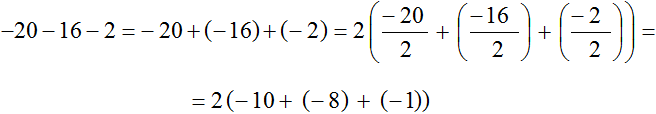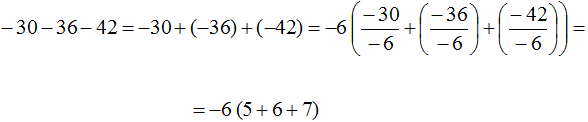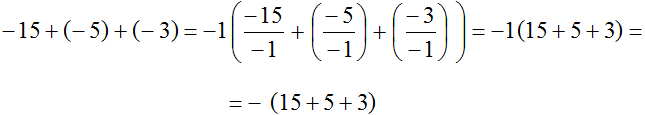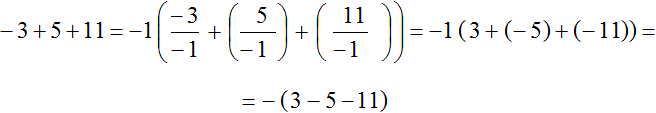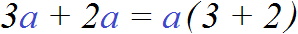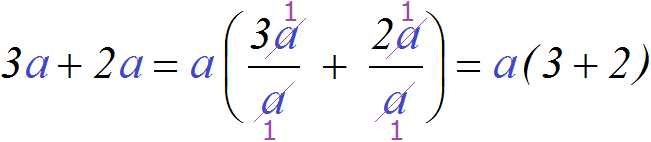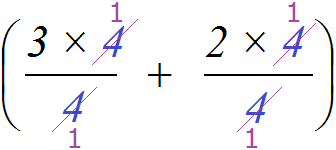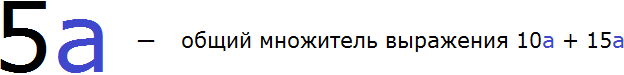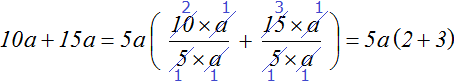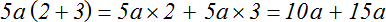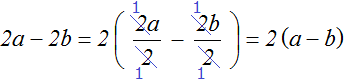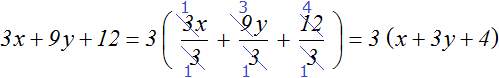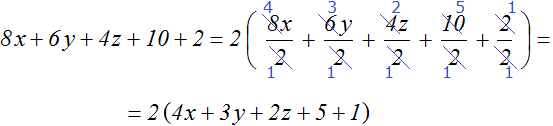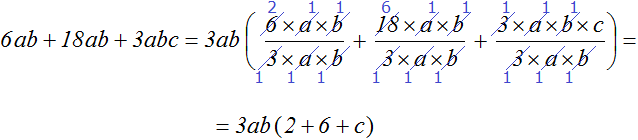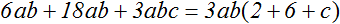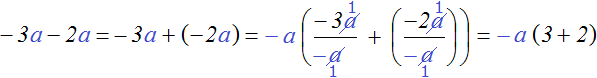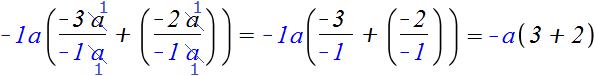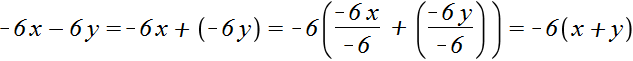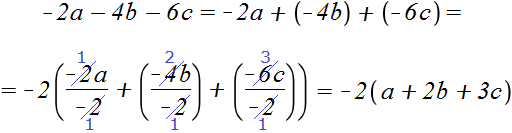Уравнение с множителями в скобках

Вынесение общего множителя за скобки

О чем эта статья:

5 класс, 6 класс, 7 класс

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).

Понятие вынесения множителя за скобки

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

Есть несколько способов разложения многочлена на множители. Один из них — вынесение общего множителя за скобки.

Вынести общий множитель за скобки можно в выражениях, которые представляют из себя суммы, в которых каждое слагаемое является произведением, причем в каждом произведении есть один одинаковый для всех множитель. Он так и называется — общий множитель.

Вынесение общего множителя за скобки — это преобразование многочлена в произведение с помощью распределительного свойства умножения. Только в случае вынесения множителя за скобки это свойство применяется справа налево.

Формула вынесения общего множителя за скобки:

Покажем метод вынесения общего множителя за скобки на примере с цифрами:

Определение общего множителя для всех членов многочлена производится пошагово:

1. Если у каждого члена есть коэффициент — находим число, на которое делится коэффициент каждого члена, и выносим его за скобки.
2. Находим переменные, которые встречаются в каждом члене. Переменные выносятся за скобки в наименьшей встречающейся степени.
3. Определяем многочлен, который должен остаться в скобках. При этом многочлен должен иметь столько же членов, сколько было в исходном многочлене.

Если нам дано произведение 6 * 2 и 6 * 5, то мы можем вынести за скобки общий множитель 5. В чем состоит данное преобразование? Мы представляем исходное выражение как произведение общего множителя и выражения в скобках, которое содержит сумму всех исходных слагаемых, кроме общего множителя.

Итак, вынесем общий множитель 5 в 6 * 2 и 6 * 5 и получим 6 * (2 + 5).

Итоговое выражение — это произведение общего множителя 6 на выражение в скобках, которое является суммой исходных слагаемых без 6.

Так и получается: 6 * 2 + 6 * 5 = 6 * (2 + 5).

Правило вынесения общего множителя за скобки

Основное правило вынесения общего множителя за скобки

Чтобы вынести за скобки общий множитель, нужно записать исходное выражение в виде произведения общего множителя и скобок, которые включают в себя исходную сумму без общего множителя.

Алгоритм вынесения общего множителя за скобки:

1. Найти наибольший общий делитель коэффициентов всех одночленов, которые входят в многочлен. Он и будет общим числовым множителем.
2. Найти общую буквенную часть для всех членов многочлена. При этом выбрать наименьший показатель степени.
3. Произведение коэффициента и общей буквенной части, которые мы нашли на первом и втором шагах, является общим множителем, который выносим за скобки.
4. Делим каждый член многочлена на вынесенный множитель и полученный результат записываем в скобках.

Важно! В скобках должно быть столько одночленов, сколько их было в многочлене.

Рассмотрим простой пример вынесения. Дано числовое выражение 4 * 7 + 4 * 3 — 4 * 5, которое является суммой трех слагаемых и общего множителя 4. Возьмем за основу выведенное правило и запишем произведение иначе: 4 * (7 + 3 — 5).

Это и есть итог нашего преобразования. Запись всего решения выглядит так:

4 * 7 + 4 * 3 — 4 * 5 = 4 * (7 + 3 — 5).

Определить сразу, какой множитель является общим, получается не всегда. Иногда выражение нужно предварительно преобразовать, заменив числа и выражения тождественно равными им произведениями.

Рассмотрим разложение многочлена на множители методом вынесения за скобки общего множителя на примере многочлена: 12m — 6m — 3m. Ход решения:

Курсы ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Вынесение минуса за скобки

Еще один случай, на котором следует обратить внимание — это вынесение за скобки минуса. Только мы выносим не сам знак, а минус единицу. Часто это помогает упростить выражение и сделать его проще.

Пример 1. Вынести минус за скобки в выражении: -10 + (-1) + (-3)

Чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые с противоположными знаками:

Найдем решение для каждого выражения:

-(10 + 1 + 3) = -(14) = -14

Поэтому между выражениями можно поставить знак равенства, потому что они равны одному и тому же значению:

-10 + (-1) + (-3) = -(10 + 1 + 3)

Пример 2. Вынести минус за скобки в выражении: -3 + 5 + 11

Ставим минус и рядом в скобках записываем выражение с противоположным знаком у каждого слагаемого:

-3 + 5 + 11 = -(3 — 5 — 11)

Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица.

Разложение многочленов на множители с примерами решения

Содержание:

Разложение многочленов на множители

Разложение многочленов на множители — операция, об-I ратная умножению многочленов. Как вы уже знаете, решая разные задачи, иногда умножают два или более чисел, а иногда — раскладывают данное число на множители. Подобные задачи возникают и при преобразовании целых алгебраических выражений. В этой главе вы узнаете о:

• вынесении общего множителя за скобки;
• способе группировки;
• формулах сокращённого умножения;
• применении разных способов разложения многочленов на множители.

Вынесение общего множителя за скобки

Вы уже умеете раскладывать на множители натуральные числа. Например,

На множители раскладывают и многочлены. Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену. Например, многочлен

Один из способов разложения многочленов на множители — вынесение общего множителя за скобки. Рассмотрим его.

Каждый член многочлена ах + ау имеет общий множитель а. На основании распределительного закона умножения 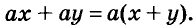Это означает, что данный многочлен ах + ау разложен на два множителя:

Чтобы убедиться, правильно ли разложен многочлен на множители, нужно выполнить умножение полученных множителей. Если всё верно, то в результате должен получиться данный многочлен.

Иногда приходится раскладывать на множители и выражения, имеющие общий многочленный множитель. Например, в выражении 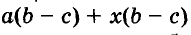общий множитель b — с. Его также можно выносить за скобки:

Один и тот же многочлен можно разложить на множители по-разному. Например,

Как правило, стараются вынести за скобки такой общий множитель, чтобы в скобках осталось простейшее выражение. Поэтому чаще всего в качестве коэффициента общего множителя берут наибольший общий делитель (НОД) коэффициентов всех членов данного многочлена или их модулей. Но не всегда. Все зависит от того, с какой целью раскладывают на множители многочлен.

Пусть, например, надо найти значение выражения 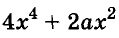при условии, когда

Чтобы использовать условие, это упражнение можно решить так:

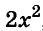
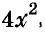
Здесь вынесено за скобки не , а тогда в скобках имеем выражение, значение которого известно из условия.

Пример:

Разложите на множители многочлен

Решение:

или

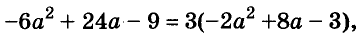
Пример:

Разложите на множители многочлен

Решение:

Пример:

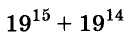
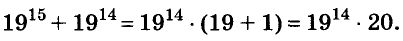
Докажите, что число делится на 20.

Последнее произведение делится на 20, поэтому делится на 20 и данная сумма.

Пример:

Решите уравнение

Решение:

поэтому данное уравнение равносильно уравнению Произведение двух чисел равно нулю тогда, когда хотя бы одно из них равно нулю.

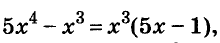
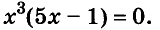
Значит, 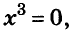отсюда х = 0, или 5х — 1 = 0, отсюда х = 0,2.

Ответ. Уравнение имеет два корня: 0 и 0,2.

Способ группировки

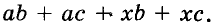
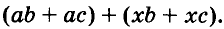
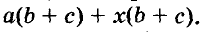
Разложим на множители многочлен Сгруппируем его члены так, чтобы слагаемые в каждой группе имели общий множитель Вынесем из первой группы за скобки общий множитель а, из второй — общий множитель х, получим выражение Слагаемые этого выражения имеют общий множитель b + с, вынесем его за скобки, получим выражение

Указанные преобразования можно записать цепочкой:

Такой способ разложения многочленов на множители называют способом группировки.

Замечание. Раскладывая на множители представленный выше многочлен, можно сгруппировать его члены иначе:

Получили такой же результат.

Разложим на множители многочлен

Записывать сумму а + с в виде 1 (а + с) необязательно, но сначала, чтобы не допускать ошибок, можно писать и так.

Чтобы воспользоваться способом группировки, иногда приходится один член данного многочлена представлять в виде суммы или разности одночленов. Чтобы разложить на множители трёхчлен 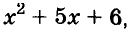• запишем одночлен

Подобные преобразования также можно выполнять, используя тождества.

Пример:

Разложите на множители многочлен:

Решение:

Ответ.

Пример:

Решите уравнение:

Решение:

Разложим левую часть уравнения на множители:

Корнем первого уравнения является у = 1,5, а второе уравнение корней не имеет, так как

Квадрат двучлена

Решая различные задачи, часто приходится умножать двучлены вида 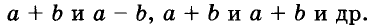Чтобы в таких случаях можно было сразу написать ответ, полезно запомнить тождества, которые называют формулами сокращённого умножения. Рассмотрим некоторые из них.

Умножим двучлен

Следовательно,

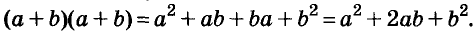
Квадрат двучлена равен квадрату первого его члена плюс удвоенное произведение первого на второй плюс квадрат второго члена.

Доказанное равенство — тождество, его называют формулой квадрата двучлена. Пользуясь ею, можно сразу записать:

Промежуточные преобразования желательно выполнять устно, тем самым сокращается запись:

По формуле квадрата двучлена можно возводить в квадрат любые двучлены, в том числе

Формулы квадрата двучлена используют и в «обратном направлении»:

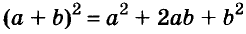
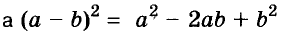
Формулу часто называют формулой квадрата суммы двух выражений, — квадрата разности двух выражений.

Для положительных чисел а и b формулу

можно доказать геометрически, как показано на рисунке 44. Так её доказывали ещё древние греки. Ведь площадь квадрата со стороной а + b равна сумме площадей квадратов а также прямоугольников ab и ab.

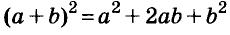
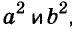
Существуют и другие формулы сокращённого умножения:

Пример:

Возведите в квадрат двучлен

Решение:

Пример:

Упростите выражение

Решение:

Пример:

Представьте в виде многочлена выражение:

Решение:

Пример:

Представьте выражение в виде степени двучлена:

Решение:

Разность квадратов

Умножим сумму переменных а и b на их разность.

Значит,

Это равенство — тождество. Словами его читают так:

Произведение суммы двух выражений и их разности равно разности квадратов этих выражений.

Пользуясь доказанной формулой, можно сразу записать:

Левую и правую части доказанной формулы можно поменять местами. Получим формулу разности квадратов двух выражений:

Разность квадратов двух выражений равна произведению их суммы и разности.

Пример:

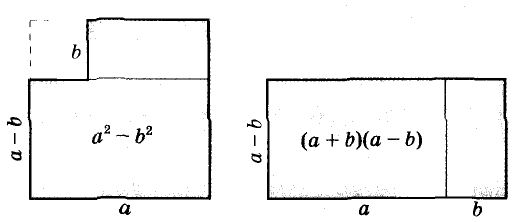
Формула разности квадратов очень удобна для разложения многочленов на множители.

Для положительных чисел а и b формулу 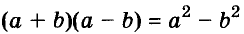можно проиллюстрировать геометрически (рис. 46). Но это тождество верно не только для положительных чисел, но и для любых других чисел и выражений.

Истинность формулы разности квадратов следует из правила умножения многочленов, а это правило — из законов действий сложения и умножения. Законы сложения и умножения чисел — это своеобразные аксиомы, следствиями которых являются алгебраические тождества.

Пример:

Напишите разность квадратов и квадрат разности выражений

Решение:

— разность квадратов; — квадрат разности данных выражений.

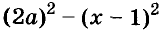
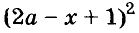
Пример:

Запишите в виде произведения двух двучленов выражение:

Решение:

Пример:

Представьте в виде двучлена выражение:

Решение:

.

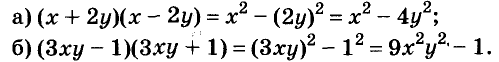
Используя формулу разности квадратов, промежуточные вычисления и преобразования можно выполнять устно, а записывать лишь конечный результат.

Использование формул сокращённого умножения

С помощью формул сокращённого умножения некоторые многочлены можно разложить на множители. Например, двучлен 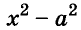можно представить в виде произведения по формуле разности квадратов:

Примеры:

Трёхчлены 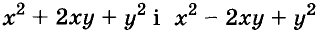раскладывают на множители по формуле квадрата двучлена:

Примеры:

Полученные, выражения можно разложить на множители и записать так:

Многочлен 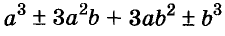можно разложить на множители по формуле куба двучлена:

Раскладывать на множители можно не только многочлены, но и некоторые другие целые выражения.

Например, 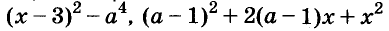— не многочлены, но и их можно представить в виде произведений многочленов:

Пример:

Разложите на множители многочлен:

Решение:

Пример:

Решите уравнение

Решение:

Значит, данное уравнение равносильно такому:

Квадрат числа равен нулю только тогда, когда это число равно 0. А х — 2 = 0, когда х = 2.

Пример:

Разложите на множители многочлен:

Решение:

Разность и сумма кубов

Выполним умножение многочленов

Следовательно, при любых значениях а и b

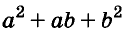
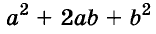
Трёхчлен называют неполным квадратом суммы выражений а и b (от он отличается только коэффициентом среднего члена). Поэтому доказанную формулу словами читают так:

разность кубов двух выражений равна произведению разности этих выражений и неполного квадрата их суммы.

Выполним умножение многочленов

Трёхчлен 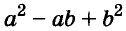называют неполным квадратом разности выражений а и b. Поэтому полученную формулу читаю так:

сумма кубов двух выражений равна произведению суммы этих выражений и неполного квадрата их разности.

С помощью доказанных формул можно раскладывать на множители многочлены, являющиеся разностями или суммами кубов.

Примеры:

Формулу «разность кубов» для положительных значений а и b можно проиллюстрировать геометрически, как показано на рисунке 49.

Если умножить на а — b выражения то получим формулы:

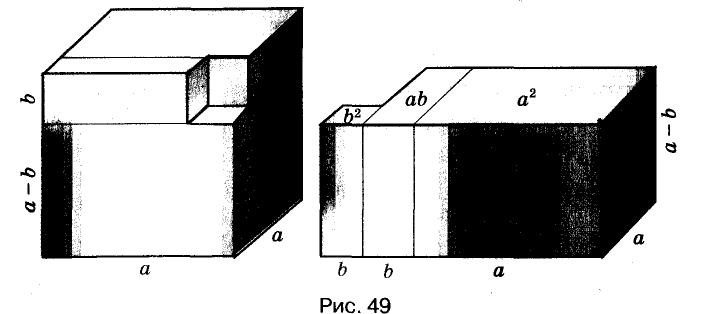
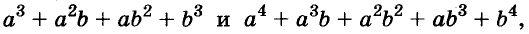
Можно доказать, что для каждого натурального значения n истинна формула:

Формулы «разность квадратов» и «разность кубов» — простейшие случаи этой общей формулы.

Пример:

Разложите на множители двучлен:

Решение:

Пример:

Найдите произведение многочленов: •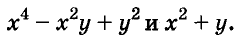

Решение:

Первый способ. По формуле суммы кубов:

Второй способ. По правилу умножения многочленов:

Применение разных способов разложения многочленов на множители

Чтобы разложить многочлен на множители, иногда приходится применять несколько способов.

Пример:

Разложите на множители многочлен

Решение:

Сначала за скобки вынесен общий множитель а, потом выражение в скобках разложено на множители по формуле разности квадратов.

Пример:

Разложите на множители выражение

Решение:

Здесь применены способ группировки, вынесение общего множителя за скобки и формула суммы кубов.

Чтобы разложить на множители более сложные многочлены, приходится применять несколько известных способов или искусственные приёмы.

В этом случае можно использовать такое правило-ориентир:

1. Вынести общий множитель (если он есть) за скобки.
2. Проверить, не является ли выражение в скобках разностью квадратов, разностью или суммой кубов.
3. Если это трёхчлен, то проверить, не является ли он квадратом двучлена.
4. Если многочлен содержит больше трёх членов, то надо попробовать группировать их и к каждой группе применить п. 1—3.

Иногда удаётся разложить многочлен на множители, прибавляя и вычитая из него одно и то же выражение.

Пример:

Разложите на множители двучлен

Решение:

Прибавим к данному двучлену выражение

Пример:

Разложите на множители выражение

Решение:

Пример:

Представьте многочлен 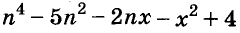в виде разности квадратов двух многочленов.

Решение:

Пример:

Докажите, что число 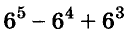делится на 31.

Последнее произведение делится на 31, поэтому делится на 31 и равное ему данное числовое выражение.

Исторические сведения:

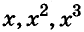
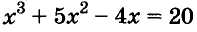
Наибольший вклад в развитие алгебраической символики внёс известный французский математик Ф. Виет, которого называли «отцом алгебры ». Он часто использовал буквенные обозначения. Вместо писал соответственно N,Q,C — первые буквы латинских слов Numerus (число), Quadratus (квадрат), Cubus (куб). Уравнение Ф. Виет записывал так:

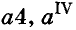
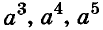
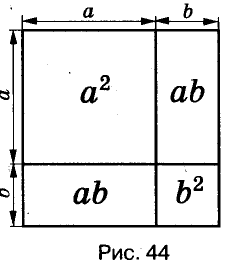
Степени чисел продолжительное время не имели специальных обозначений, четвёртую степень числа а записывали в виде произведения аааа. Позднее такое произведение начали записывать . Записи предложил Р. Декарт.

Формулы сокращённого умножения древним китайским и греческим математикам были известны за много веков до начала нашей эры. Записывали их тогда не с помощью букв, а словами и доказывали геометрически (только для положительных чисел). Пользуясь рисунком, объясняли, что для любых чисел а и b площадь квадрата со стороной а + b равна сумме площадей двух квадратов со сторонами а и b к двух прямоугольников со сторонами а, b. Итак, 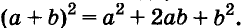Подобным способом обосновали и другие равенства, которые. мы теперь называем формулами сокращённого умножения.

В учебнике рассмотрены простейшие формулы сокращённого умножения.

Формулы квадрата и куба двучлена — простейшие случаи общей формулы бинома Ньютона:

Напомню:

Разложить многочлен на множители — это означает заменить его произведением нескольких многочленов, тождественным данному многочлену.

Простейшие способы разложения многочленов на множители:

• вынесение общего множителя за скобки;
• способ группировки;
• использование формул сокращённого умножения.

Примеры:

Формулы сокращённого умножения

Разложение многочленов на множители — это преобразование, обратное умножению многочленов. Схематично эти две операции можно изобразить, например, так.

• Системы линейных уравнений с двумя переменными
• Рациональные выражения
• Квадратные корни
• Квадратные уравнения
• Целые выражения
• Одночлены
• Многочлены
• Формулы сокращенного умножения

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Вынесение общего множителя за скобки

Продолжаем разбираться с основами алгебры. Сегодня мы поработаем с распределительным законом умножения, а именно рассмотрим такое действие как вынесение общего множителя за скобки .

Основной принцип

Распределительный закон умножения позволяет умножить число на сумму (или сумму на число). Например, чтобы найти значение выражения 3 × (4 + 5) можно умножить число 3 на каждое слагаемое в скобках и сложить полученные результаты:

3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15

Число 3 и выражение в скобках можно поменять местами (это следует из переместительного закона умножения). Тогда каждое слагаемое, которое в скобках, будет умножено на число 3

(4 + 5) × 3 = 4 × 3 + 5 × 3 = 12 + 15

Пока не будем вычислять конструкцию 3 × 4 + 3 × 5 и складывать полученные результаты 12 и 15 . Оставим выражение в виде 3 (4 + 5) = 3 × 4 + 3 × 5 . Ниже оно нам потребуется именно в таком виде, чтобы понять суть вынесения общего множителя за скобки.

Распределительный закон умножения иногда называют внесением множителя во внутрь скобок. В выражении 3 × (4 + 5) множитель 3 был за скобками. Умножив его на каждое слагаемое в скобках, мы по сути внесли его во внутрь скобок. Для наглядности можно так и записать, хоть и не принято так записывать:

3 (4 + 5) = ( 3 × 4 + 3 × 5)

Поскольку в выражении 3 × (4 + 5) число 3 умножается на каждое слагаемое в скобках, это число является общим множителем для слагаемых 4 и 5

Как говорилось ранее, умножив этот общий множитель на каждое слагаемое в скобках, мы вносим его во внутрь скобок. Но возможен и обратный процесс — общий множитель можно обратно вынести за скобки. В данном случае в выражении 3 × 4 + 3 × 5 общий множитель виден как на ладони — это множитель 3 . Его и нужно вынести за скобки. Для этого сначала записывается сам множитель 3

и рядом в скобках записывается выражение 3 × 4 + 3 × 5 но уже без общего множителя 3 , поскольку он вынесен за скобки

В результате вынесения общего множителя за скобки получается выражение 3 (4 + 5) . Это выражение тождественно равно предыдущему выражению 3 × 4 + 3 × 5

3 (4 + 5) = 3 × 4 + 3 × 5

Если вычислить обе части полученного равенства, то получим тождество:

3 (4 + 5) = 3 × 4 + 3 × 5

Как происходит вынесение общего множителя за скобки

Вынесение общего множителя за скобки по сути является обратной операцией внесению общего множителя во внутрь скобок.

Если при внесении общего множителя внутрь скобок, мы умножаем этот множитель на каждое слагаемое в скобках, то при вынесении этого множителя обратно за скобки, мы должны разделить каждое слагаемое в скобках на этот множитель.

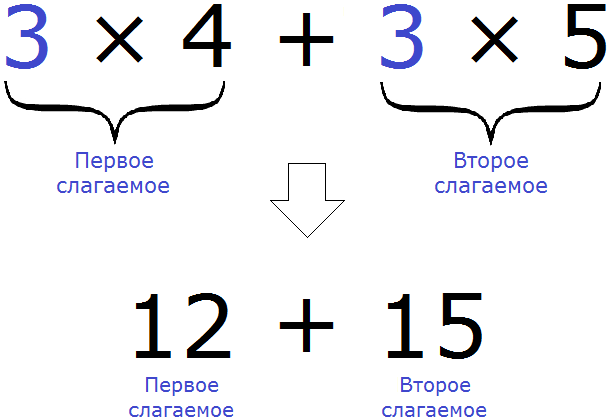
В выражении 3 × 4 + 3 × 5 , которое было рассмотрено выше, так и происходило. Каждое слагаемое было разделено на общий множитель 3 . Произведения 3 × 4 и 3 × 5 и являются слагаемыми, поскольку если их вычислить, мы получим сумму 12 + 15

Теперь мы можем детально увидеть, как происходит вынесение общего множителя за скобки:

Видно, что общий множитель 3 сначала вынесен за скобки, затем в скобках происходит деление каждого слагаемого на этот общий множитель.

Деление каждого слагаемого на общий множитель можно выполнять не только разделяя числитель на знаменатель, как это было показано выше, но и сокращая эти дроби. В обоих случаях получится один и тот же результат:

Мы рассмотрели простейший пример вынесения общего множителя за скобки, чтобы понять основной принцип.

Но не всё так просто, как кажется на первый взгляд. После того, как число умножено на каждое слагаемое в скобках, полученные результаты складывают, и общий множитель пропадает из виду.

Вернёмся к нашему примеру 3 (4 + 5) . Применим распределительный закон умножения, то есть умножим число 3 на каждое слагаемое в скобках и сложим полученные результаты:

3 × (4 + 5) = 3 × 4 + 3 × 5 = 12 + 15

После того, как вычислена конструкция 3 × 4 + 3 × 5 , мы получаем новое выражение 12 + 15 . Видим, что общий множитель 3 пропал из виду. Теперь в полученном выражении 12 + 15 попробуем обратно вынести общий множитель за скобки, но чтобы вынести этот общий множитель его сначала нужно найти.

Обычно при решении задач встречаются именно такие выражения, в которых общий множитель сначала нужно найти, прежде чем его выносить.

Чтобы в выражении 12 + 15 вынести общий множитель за скобки, нужно найти наибольший общий делитель (НОД) слагаемых 12 и 15. Найденный НОД и будет общим множителем.

Итак, найдём НОД слагаемых 12 и 15. Напомним, что для нахождения НОД необходимо разложить исходные числа на простые множители, затем выписать первое разложение и убрать из него множители, которые не входят в разложение второго числа. Оставшиеся множители нужно перемножить и получить искомый НОД. Если испытываете затруднения на этом моменте, обязательно повторите этот урок.

НОД слагаемых 12 и 15 это число 3. Данное число является общим множителем слагаемых 12 и 15. Его и нужно выносить за скобки. Для этого сначала записываем сам множитель 3 и рядом в скобках записываем новое выражение, в котором каждое слагаемое выражения 12 + 15 разделено на общий множитель 3

Ну и дальнейшее вычисление не составляет особого труда. Выражение в скобках легко вычисляется — двенадцать разделить на три будет четыре, а пятнадцать разделить на три будет пять:

Таким образом, при вынесении общего множителя за скобки в выражении 12 + 15 получается выражение 3(4 + 5) . Подробное решение выглядит следующим образом:

В коротком решении пропускают запись в которой показано, как каждое слагаемое разделено на общий множитель:

Пример 2. Вынести общий множитель за скобки в выражении 15 + 20

Наибольший общий делитель слагаемых 15 и 20 это число 5. Данное число является общим множителем слагаемых 15 и 20. Его и вынесем за скобки:

Получили выражение 5(3 + 4).

Получившееся выражение 5(3 + 4) можно проверить. Для этого достаточно умножить пятёрку на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 15 + 20

Пример 3. Вынести общий множитель за скобки в выражении 18 + 24 + 36

Найдём НОД слагаемых 18, 24 и 36. Чтобы найти НОД нескольких чисел, нужно разложить эти числа на простые множители, затем найти произведение общих множителей:

НОД слагаемых 18, 24 и 36 это число 6. Данное число является общим множителем слагаемых 18, 24 и 36. Его и вынесем за скобки:

Проверим получившееся выражение. Для этого умножим число 6 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 18 + 24 + 36

Пример 4. Вынести общий множитель за скобки в выражении 13 + 5

Слагаемые 13 и 5 являются простыми числами. Они раскладываются только на единицу и самих себя:

Это значит, что у слагаемых 13 и 5 нет общих множителей, кроме единицы. Соответственно, нет смысла выносить эту единицу за скобки, поскольку это ничего не даст. Покажем это:

Пример 5. Вынести общий множитель за скобки в выражении 195 + 156 + 260

Найдём НОД слагаемых 195, 156 и 260

НОД слагаемых 195, 156 и 260 это число 13. Данное число является общим множителем для слагаемых 195, 156 и 260. Его и вынесем за скобки:

Проверим получившееся выражение. Для этого умножим 13 на каждое слагаемое в скобках. Если мы всё сделали правильно, то должны получить выражение 195 + 156 + 260

Выражение, в котором требуется вынести общий множитель за скобки, может быть не только суммой чисел, но и разностью. Например, вынесем общий множитель за скобки в выражении 16 − 12 − 4. Наибольшим общим делителем чисел 16, 12 и 4 это число 4. Данное число и вынесем за скобки:

Проверим получившееся выражение. Для этого умножим четвёрку на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 16 − 12 − 4

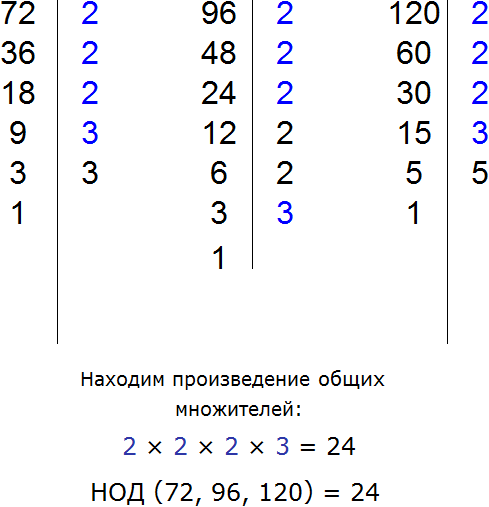
Пример 6. Вынести общий множитель за скобки в выражении 72 + 96 − 120

Найдём НОД чисел 72, 96 и 120

НОД для 72, 96 и 120 это число 24. Данное число является общим множителем слагаемых 195, 156 и 260. Его и вынесем за скобки:

Проверим получившееся выражение. Для этого умножим 24 на каждое число в скобках. Если мы всё сделали правильно, то должны получить выражение 72+96−120

Общий множитель, выносимый за скобки, может быть и отрицательным. Например, вынесем общий множитель за скобки в выражении −6 − 3. Вынести общий множитель за скобки в таком выражении можно двумя способами. Рассмотрим каждый из них.

Способ 1.

Заменим вычитание сложением:

Теперь находим общий множитель. Общим множителем данного выражения будет наибольший общий делитель модулей слагаемых −6 и −3.

Модуль первого слагаемого это 6. А модуль второго слагаемого это 3. НОД(6 и 3) равен 3. Данное число является общим множителем слагаемых 6 и 3. Его и вынесем за скобки:

Выражение полученное таким способом получилось не очень аккуратным. Много скобок и отрицательных чисел не придают выражению простоту. Поэтому можно воспользоваться вторым способом, суть которого заключается в том, чтобы вынести за скобки не 3, а −3.

Способ 2.

Как и в прошлый раз заменяем вычитание сложением

В этот раз мы вынесем за скобки не 3, а −3

Выражение полученное в этот раз выглядит намного проще. Запишем решение покороче, чтобы сделать его ещё проще:

Разрешать выносить отрицательный множитель за скобки связано с тем, что разложение чисел −6 и (−3) можно записать двумя видами: сначала сделать множимое отрицательным, а множитель положительным:

во втором случае множимое можно сделать положительным, а множитель отрицательным:

А значит мы вольны выносить за скобки тот сомножитель, который захотим.

Пример 8. Вынести общий множитель за скобки в выражении −20 − 16 − 2

Заменим вычитание сложением

−20 − 16 − 2 = −20 + (−16) + (−2)

Наибольшим общим делителем слагаемых −20, −16 и −2 является число 2. Это число является общим множителем этих слагаемых. Посмотрим, как это выглядит:

Но приведенные разложения можно заменить на тождественно равные разложения. Различие будет в том, что общим множителем будет не 2 , а −2

Поэтому для удобства за скобки можно вынести не 2 , а −2

Запишем приведенное решение покороче:

А если бы мы вынесли за скобки 2 , то получилось бы не совсем аккуратное выражение:

Пример 9. Вынести общий множитель за скобки в выражении −30 − 36 − 42

Заменим вычитание сложением:

Наибольшим общим делителем слагаемых −30, −36 и −42 это число 6. Данное число является общим множителем для этих слагаемых. Но за скобки мы вынесем не 6, а −6 поскольку числа −30, −36 и −42 можно представить так:

Вынесение минуса за скобки

При решении задач иногда может быть полезным вынесение минуса за скобки. Это позволяет упростить выражение и сделать его проще.

Рассмотрим следующий пример. Вынести минус за скобки в выражении −15 + (−5) + (−3)

Для наглядности заключим данное выражение в скобки, ведь речь идёт о том, чтобы вынести минус за эти скобки

Итак, чтобы вынести минус за скобки, нужно записать перед скобками минус и в скобках записать все слагаемые, но с противоположными знаками. Знаки операций (то есть плюсы) оставляем без изменений:

Мы вынесли минус за скобки в выражении −15 + (−5) + (−3) и получили −(15 + 5 + 3) . Оба выражения равны одному и тому же значению −23

−(15 + 5 + 3) = −(23) = −23

Поэтому между выражениями −15 + (−5) + (−3) и −(15 + 5 + 3) можно поставить знак равенства, потому что они равны одному и тому же значению:

−15 + (−5) + (−3) = −(15 + 5 + 3)

На самом деле при вынесении минуса за скобки опять же срабатывает распределительный закон умножения:

Если поменять местами левую и правую часть этого тождества, то получится, что сомножитель a вынесен за скобки

Тоже самое происходит, когда мы выносим общий множитель в других выражениях и когда выносим минус за скобки.

Очевидно, что при вынесении минуса за скобки, выносится не минус, а минус единица. Ранее мы говорили, что коэффициент 1 принято не записывать.

Поэтому и образуется перед скобками минус, а знаки слагаемых которые были в скобках меняют свой знак на противоположный, поскольку каждое слагаемое разделено на минус единицу.

Вернёмся к предыдущему примеру и детально увидим, как на самом деле выносился минус за скобки

Пример 2. Вынести минус за скобки в выражении −3 + 5 + 11

Ставим минус и рядом в скобках записываем выражение −3 + 5 + 11 с противоположным знаком у каждого слагаемого:

−3 + 5 + 11 = −(3 − 5 − 11)

Как и в прошлом примере, здесь за скобки вынесен не минус, а минус единица. Подробное решение выглядит следующим образом:

Сначала получилось выражение −1(3 + (−5) + (−11)) , но мы раскрыли в нём внутренние скобки и получили выражение −(3 − 5 − 11) . Раскрытие скобок это тема следующего урока, поэтому если данный пример вызывает у вас затруднения, можете пока пропустить его.

Вынесение общего множителя за скобки в буквенном выражении

Выносить общий множитель за скобки в буквенном выражении намного интереснее.

Для начала рассмотрим простейший пример. Пусть имеется выражение 3 a + 2 a . Вынесем общий множитель за скобки.

В данном случае, общий множитель виден невооруженным глазом — это множитель a . Его и вынесем за скобки. Для этого записываем сам множитель a и рядом в скобках записываем выражение 3 a + 2 a , но уже без множителя a поскольку он вынесен за скобки:

Как и в случае с числовым выражением, здесь происходит деление каждого слагаемого на вынесенный общий множитель. Выглядит это так:

В обеих дробях переменные a были сокращены на a . Вместо них в числителе и в знаменателе получились единицы. Единицы получились по причине того, что вместо переменной a может стоять любое число. Эта переменная располагалась и в числителе и в знаменателе. А если в числителе и в знаменателе располагаются одинаковые числа, то наибольший общий делитель для них будет само это число.

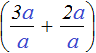
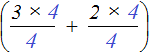
Например, если вместо переменной a подставить число 4, то конструкция примет следующий вид: . Тогда четвёрки в обеих дробях можно будет сократить на 4:

Получается то же самое, что и раньше, когда вместо четвёрок стояла переменная a .

Поэтому не следует пугаться при виде сокращения переменных. Переменная это полноправный множитель, пусть даже выраженный буквой. Такой множитель можно выносить за скобки, сокращать и выполнять другие действия, которые допустимы к обычным числам.

Буквенное выражение содержит не только числа, но и буквы (переменные). Поэтому общий множитель, который выносится за скобки часто бывает буквенным множителем, состоящим из числа и буквы (коэффициента и переменной). К примеру, следующие выражения являются буквенными множителями:

Прежде чем выносить такой множитель за скобки, нужно определиться, какое число будет в числовой части общего множителя и какая переменная будет в буквенной части общего множителя. Другими словами, нужно узнать какой коэффициент будет у общего множителя и какая переменная будет в него входить.

Рассмотрим выражение 10a + 15a . Попробуем вынести в нём общий множитель за скобки. Сначала определимся из чего будет состоять общий множитель, то есть узнаем его коэффициент и какая переменная будет в него входить.

Коэффициентом общего множителя должен быть наибольший общий делитель коэффициентов буквенного выражения 10a + 15a . Коэффициентами данного выражения являются числа 10 и 15 , а их наибольший общий делитель это число 5 . Значит число 5 будет коэффициентом общего множителя, выносимого за скобки.

Теперь определимся какая переменная будет входить в общий множитель. Для этого нужно посмотреть на выражение 10a + 15a и найти буквенный сомножитель, который входит во все слагаемые. В данном случае, это сомножитель a . Этот сомножитель входит в каждое слагаемое выражения 10a + 15a . Значит переменная a будет входить в буквенную часть общего множителя, выносимого за скобки:

Теперь осталось вынести общий множитель 5a за скобки. Для этого разделим каждое слагаемое выражения 10a + 15a на 5a . Для наглядности коэффициенты и числа будем отделять знаком умножения (×)

Проверим получившееся выражение. Для этого умножим 5a на каждое слагаемое в скобках. Если мы всё сделали правильно, то получим выражение 10a + 15a

Буквенный множитель не всегда можно вынести за скобки. Иногда общий множитель состоит только из числа, поскольку ничего подходящего для буквенной части в выражении не находится.

Например, вынесем общий множитель за скобки в выражении 2a − 2b . Здесь общим множителем будет только число 2, а среди буквенных сомножителей общих множителей в выражении нет. Поэтому в данном случае будет вынесен только множитель 2

Пример 2. Вынести общий множитель выражении 3x + 9y + 12

Коэффициентами данного выражения являются числа 3, 9 и 12, их НОД равен 3. Значит коэффициентом общего множителя, выносимого за скобки, будет число 3. А среди буквенных сомножителей (переменных) нет общего множителя. Поэтому окончательный общий множитель это 3

Пример 3. Вынести общий множитель за скобки в выражении 8x + 6y + 4z + 10 + 2

Коэффициентами данного выражения являются числа 8, 6, 4, 10 и 2, их НОД равен 2. Значит коэффициентом общего множителя, выносимого за скобки, будет число 2. А среди буквенных сомножителей нет общего множителя. Поэтому окончательный общий множитель это 2

Пример 4. Вынести общий множитель 6ab + 18ab + 3abc

Коэффициентами данного выражения являются числа 6, 18 и 3, их НОД равен 3. Значит коэффициентом общего множителя, выносимого за скобки, будет число 3. В буквенную часть общего множителя будут входить переменные a и b, поскольку в выражении 6ab + 18ab + 3abc эти две переменные входят в каждое слагаемое. Поэтому окончательный общий множитель это 3ab

При подробном решении выражение становится громоздким и даже непонятным. В данном примере это более чем заметно. Это связано с тем, что мы сокращаем множители в числителе и в знаменателе. Лучше всего делать это в уме и сразу записывать результаты деления. Тогда выражение станет коротким и аккуратным:

Как и в случае с числовым выражением в буквенном выражении общий множитель может быть и отрицательным.

Например, вынесем общий множитель за скобки в выражении −3 a − 2 a .

Для удобства заменим вычитание сложением

−3 a − 2 a = −3 a + (−2 a )

Общим множителем в данном выражении является множитель a . Но за скобки можно вынести не только a , но и −a . Его и вынесем за скобки:

Получилось аккуратное выражение −a (3+2). Не следует забывать, что множитель −a на самом деле выглядел как −1a и после сокращения в обеих дробях переменных a , в знаменателях остались минус единицы. Поэтому в итоге и получаются положительные ответы в скобках

Пример 6. Вынести общий множитель за скобки в выражении −6x − 6y

Заменим вычитание сложением

Вынесем за скобки −6

Запишем решение покороче:

Пример 7. Вынести общий множитель за скобки в выражении −2a − 4b − 6c

Заменим вычитание сложением

Вынесем за скобки −2

Запишем решение покороче:

−2a − 4b − 6c = −2(a + 2b + 3c)

Вынесение общего множителя за скобки это очень важная тема. В данном уроке рассмотрены только азы и простейшие примеры. Мы ещё вернемся к этой теме, когда будем изучать многочлены.

Обязательно изучите данный урок, поскольку при изучении многочленов потребуется выносить за скобки сложный множитель, состоящий из степеней.