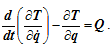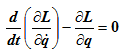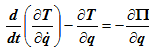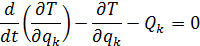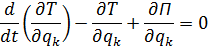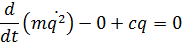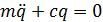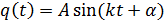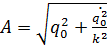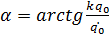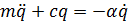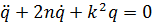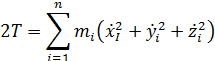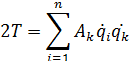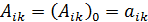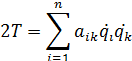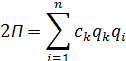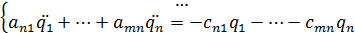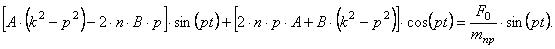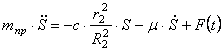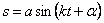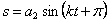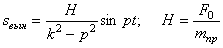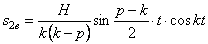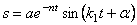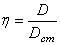iSopromat.ru
Рассмотрим уравнения Лагранжа второго рода для механической системы имеющей одну степень свободы:
В случае если механическая система имеет одну степень свободы ( s = 1), положение этой системы определяется одной обобщенной координатой q, которой соответствует обобщенная сила Q.
Уравнения Лагранжа второго рода для такой системы будут выглядеть так:
В случае, если система является консервативной (т.е. все активные силы, действующие на систему, являются потенциальными), уравнения Лагранжа второго рода для такой системы будут выглядеть так:
Для решения задач часто более удобна эквивалентная форма записи:
Чтобы составить уравнения Лагранжа второго рода для системы с одной степенью свободы, следует действовать в такой последовательности:
- сделать рисунок, обозначить на нем все активные силы, приложенные к системе;
- выбрать обобщенную координату q. При этом следует помнить, что от выбора обобщенной координаты зависит объем последующих вычислений. Если есть возможность, обобщенную координату следует выбрать так, чтобы она являлась циклической;
- определить, является ли рассматриваемая система консервативной;
- если система является консервативной, следует вычислить ее кинетическую T и потенциальную энергию Π, выразив их через обобщенную координату q и обобщенную скорость q’. Если система не является консервативной, следует вычислить только ее кинетическую энергию;
- вычислить производные, входящие в уравнения Лагранжа второго рода.
Если система не консервативная, это будут производные
Если система консервативная, к ним добавится производная ∂Π/∂q;
Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах
Уравнение Лагранжа. Свободные колебания системы с одной степенью свободы (начальные условия, уравнения, определения). Свободные колебания системы при сопротивлении
Для исследования колебательных систем с конечным числом степеней свободы используются уравнения Лагранжа в обобщенных координатах, составленные в предположении о том, что связи, наложенные на систему, идеальны; уравнения не содержат реакций связей; входящие в уравнения величины, определяющие движения системы, непосредственно связаны обобщенными силами.
Для консервативных систем уравнение Лагранжа записывается через потенциальную энергию:
В этом случае энергия характеризует полную механическую энергию системы.
Колебания системы с одной степенью свободы.
Система с одной СС – система, положение которой в пространстве однозначно определяется заданием одной обобщенной координаты. Например математический маятник движется по закону 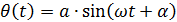
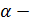
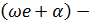
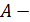
Уравнения малых свободных колебаний системы с одной СС.
Колебания называются свободными, если скорость изменения состояния системы определяется только состоянием самой системы. Такая система – линейный осциллятор.
Система консервативна, уравнение Лагранжа:
Сопротивление среды равно нулю, поэтому
Потенциальная энергия оценивается через жесткость 
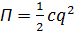
Общее решение: 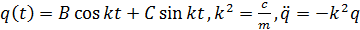
Подстановка для решения: 
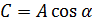
Начальные условия для решения: 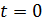
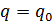

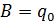
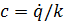
Свободные колебания при наличии сопротивления.
В этом случае на систему действует сила 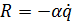
Введем отношение 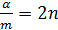
Колебания системы с конечным числом степеней свободы, приведенная система. Кинетическая и потенциальная энергия малых свободных колебаний. Уравнение малых колебаний системы около положения устойчивого равновесия.
Детали или механизмы системы на практике являются сложной упругой системой с бесконечным числом степеней свободы. Для определения положения точек при колебаниях в любой момент времени необходимо найти функцию времени и координат точек. При расчетах упругая система заменяется более простой системой с конечным числом степеней свободы – приведенная система.
Кинематическая энергия системы с 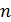
Если выполняется переход к обобщенным координатам:
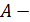
Для колебаний возле положения устойчивого равновесия разложение коэффициентов 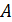

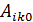
Потенциальная энергия системы может быть выражена через упругие коэффициенты:
Уравнения малых колебаний системы около положения устойчивого равновесия.
Подставляя в уравнение Лагранжа выражения для кинетической и потенциальной энергий b принимая, что: 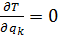
Общее решение данной системы уравнений определяет колебания механической системы.
Уравнение с одной степенью свободы
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ ПО ДИНАМИКЕ
Исследование колебаний механической системы с одной степенью свободы
Эти задачи следующие:
2. Построение расчетной схемы .
Ф ормулировка задачи — это условие ( текст) з адачи. Она осу ществляется руководител ем работ сов местно с испол нителе м.
Рас четная схема — эт о рисунок , на ко тор ом изображены :
а) ра циональ но выбранная система координат;
Математическая моде ль — э то система д иф фере нциальных уравн ений, алгебраических уравнений и на чальн ых условий, описывающих динамическое поведение механической системы.
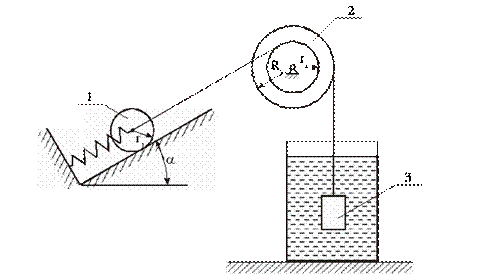
Дано: m1, m2, m3 — массы тел механической системы, с — жесткость упру гого элемента, r 1 — радиус одн ородн ого катка 1, r2, R2 — радиусы ст упеней блока 2, i2 — рад иус инерции блока 2 , 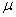
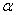
Определить: применяя основные теоремы динамики системы и аналитические методы теоретической механики, определить закон движения первого тела и реакции внешних и внутренних связей. Провести численный анализ полученного решения с использованием ЭВМ.
Порядок выполнения работы:
3) Сформулировать начальные услови я движения.
4) Найти решение дифференциального уравнения движения.
6) По дставив на йденные постоянны е интегрирования в решение дифференциального уравнения, записать закон движ ен ия объ ект а .
8) Построить алгоритм вычис лени й для реализации н а ЭВМ.
9) Произ вес ти вычисления в дисплейном классе.
10) Произв ес ти графическую обработк у результатов вычис лений.
1. Применение основных теорем динамики механической системы
1.1. Постановка второй основной задачи динамики механической системы
Расчетная схема представлена на рис.2
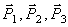
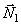
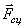
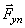
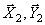
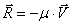
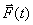
Рассматриваемая механическая система имеет одну степень свободы (нити нерастяжимые, качение катка 1 происходит без скольжения). Будем определять ее положение с помощью координаты S. Начало отсчета координаты совместим с положением статического равновесия центра масс груза 3.
Для пост роения дифферен циального уравнения движен ия с истемы используем теорему об изменении к инетической энергии механической системы в форме:
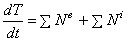
где Т — кинетическая энергия системы,
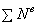
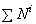
Теорема (1.1) формулируется так: «Производная по времени от кинетической энергии механической системы равн а алгебраической сумме мощностей внеш них и внутренних сил, д ейс твующих на точки механической системы».
Вычислим ки нетическую энергию сис темы как сумму кинетических эн ергий тел 1-3:
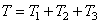
Каток 1 совершает плоскопараллельное движение, поэто му его кинетическая энергия опре деляется по теореме Кенига:
где VC1 – скорость центра масс катка;
JC1 – момент инерции относительно центральной оси катка;
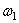
Блок 2 совершает вращ ательное движение около неподвижной оси. Его кинетическая энергия
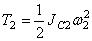
где JC2 – момент инерции относительно центральной оси блока;
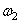
Груз 3 совершает поступательное движение. Его кинетическая энергия равна:
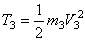
Кинетическая энергия всего механизма будет равна:
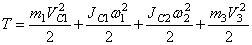
Выразим VC1, 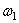
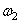
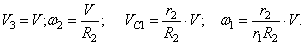
Подставляя (1.3), (1.4), (1.5) в (1.6) с учетом (1.7), получаем:
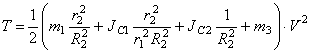
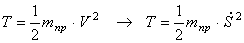
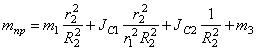
Величину 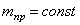
Найдем производную от кинетической энергии по времени
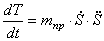
Теперь вычислим правую часть уравнения (1.1) — сумму мощностей внешних и внутренних сил.
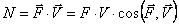
Рассматриваемая нами механическая система является неизменяемой, т.е. тела, входящие в систему, недеформируемы и скорости их точек относительно друг друга равны нулю. Поэтому сумма мощностей всех внутренних сил будет равняться нулю:
Будут равняться нулю и мощности некоторых внешних сил, приложенных в точках, скорости которых равны нулю. Как видно из расчетной схемы, таковыми являются силы
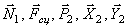
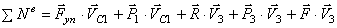
или, раскрывая скалярные произведения,
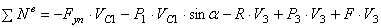
С учетом кинематических соотношений (1.7) сумму мощностей внешних сил преобразуем к виду:
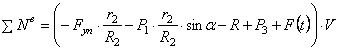
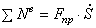
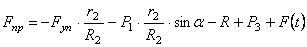
Величину F пр будем называть приведенной силой.
Преобразуем выражение (1.18). Упругую силу считаем пропорциональной удлинению пружины. Полное удлинение пружины f равно сумме статического f ст и динамического SC1 удлинений
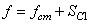
причем из выражения (1.7) для VС1 следует, что 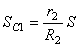
Тогда упругая сила будет равна:
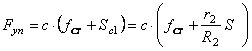
Сила вязкого сопротивления 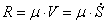
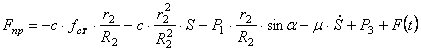
В состоянии покоя приведенная сила равна нулю. Полагая в (1.20) 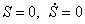
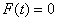
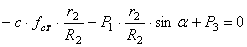
Из уравнения (1.21) определяется статическое удлинение пружины
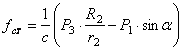
Учитывая (1.22) в (1.20), получаем окончательное выражение для приведенной силы:
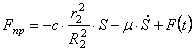
Подставим выражения для производной от кинетической энергии (1.11) и сумму мощностей всех сил (1.17) с учетом (1.23) в уравнение (1.1). Тогда, получаем дифференциальное уравнение движения системы:
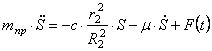
Запишем последнее уравнение в виде:
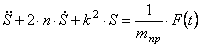
где введены коэффициенты, имеющие определенный физический смысл:
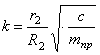
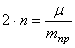
Запишем начальные условия движения:
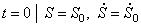
В ыражения (1.25) и (1.26) совместно представляют математическую модель для решения второй задачи динамики.
1.2. Определение закона движения системы.
Проинтегрируем дифференциальное уравнение (1.25). Пусть возмущающая сила изменяется по гармоническому закону:
где 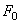
р — циклическая частота возмущения.
Общее решение S неоднородного дифференциального уравнения (1.25) складывается из общего решения однородного уравнения 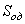
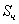
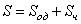
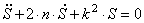
Решение этого уравнения ищем в виде функции
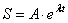
где А и 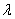
Подставляя (2.3) в (2.2), получаем:
Так как мы ищем нетривиальное решение, то 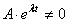
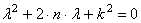
Уравнение (2.4) называется характеристическим уравнением дифференциального уравнения (2.2). Это уравнение имеет два корня:
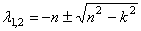
В зависимости от знака подкоренного выражения, корни характеристического уравнения могут быть комплексно-сопряженными или действительными. Возможны три случая:
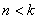
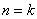
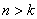
В первом случае ( 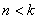
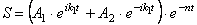
где А 1 , А2 – постоянные интегрирования,
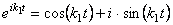
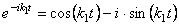
нетрудно представить в виде:
где a , 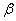
Во втором случае ( 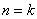
В третьем случае ( 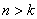
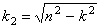
Далее предполагается, что в рассматриваемом примере имеет место случай 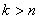
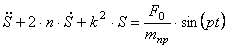
Частное решение ищем в виде правой части
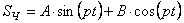
Сравнивая коэффициенты при соответствующих тригонометрических функциях справа и слева, получаем систему алгебраических уравнений для определения постоянных А и В:
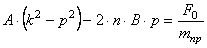
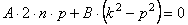
Решая эту систему, получаем следующие выражения для коэффициентов А и В:
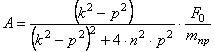
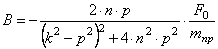
Таким образом, решение (2.12) определено. Складывая (2.8) и (2.12), получаем общее решение неоднородного уравнения (2.11)
Константы а и 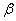
Подчинив (2.14) и (2.15) начальным условиям, получим систему уравнений относительно искомых констант
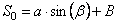
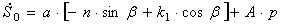
Решая эту систему, получаем:
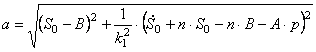
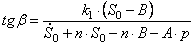
Подставляя (2.16) в (2.14), получаем закон движения механизма.
1.3. Определение реакций внешних и внутренних связей.
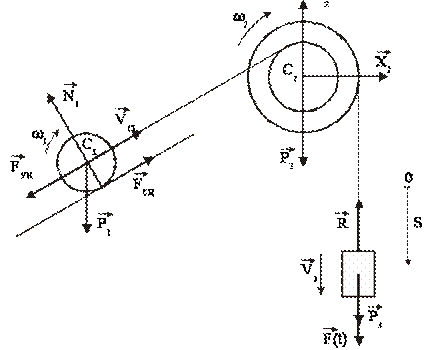
Для решения этой задачи расчленяем механизм на отдельные части и изображаем расчетные схемы отдельно для каждого тела (рис.3).
Определение реакций связей проведем с помощью теоремы об изменении количества движения
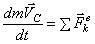
и теоремы об изменении кинетического момента относительно центра масс
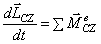
В соответствии с расчетными схемами (рис. 3) записываем уравнения (3.1) и (З.2) в проекциях на оси координат
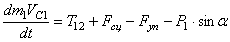
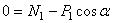
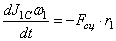
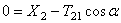
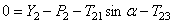
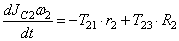
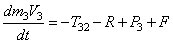
С учетом кинематических соотношений (1.7) систему уравнений (3.3) -(3.9) преобразуем к виду:
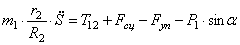
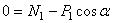
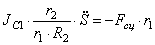
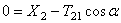
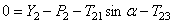
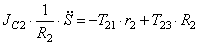
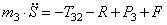
Уравнения (3.10) составляют систему алгебраических уравнений относительно функций
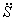
Решая эту систему, получаем и дифференциальное уравнение движения системы, и выражения для определения реакций.
2.1. Составлени е дифференциального уравнения движения механизма с помощью принципа Даламбера-Лагранжа.
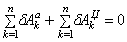
Здесь 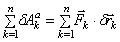
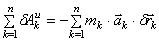
Изобразим на рисунке активные силы и силы инерции (рис.4). Реакции идеальных связей 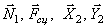
Сообщим системе возможное перемещение. Возможная работа активных сил определяется как сумма следующих элементарных работ:
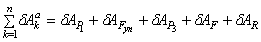
Вычисляя последовательно элементарные работы активных сил и суммируя их, получаем после несложных преобразований
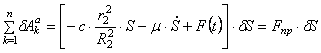
Аналогичное выражение для приведенной силы F пр получено ранее [см. (1.23)].
Найдем возможную работу сил инерции:
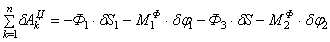
Для величин главных векторов и главных моментов сил инерции имеем следующие выражения:
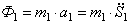
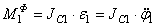
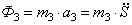
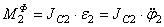
Используя кинематические соотношения (1.7), можно записать
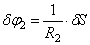
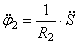
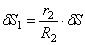
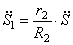
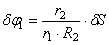
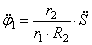
Тогда возможную работу сил инерции можно преобразовать к виду
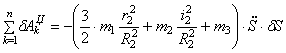
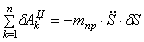
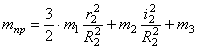
Аналогичное выражение для приведенной массы системы было получено ранее [см.(1.10)]. Подставляя выражения (4.3) и (4.8) в общее уравнение динамики (4.1), получаем
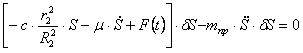
Поделив (4.10) на 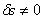
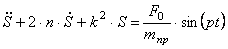
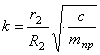
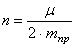
Дифференциальное уравнение (4.11) полностью совпадает с полученным ранее уравнением (1.25).
2.2. Составление дифференциального уравнения движения механизма с помощью уравнений Лагранжа 2— го рода.
Составим теперь уравнения Лагранжа 2-го рода. Для механической системы с одной степенью свободы дифференциальное уравнение движения в обобщенных координатах имеет вид:
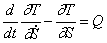
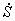
Выражение для кинетической энергии системы было найдено ранее (1.8):
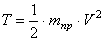
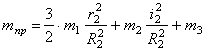
Учитывая, что 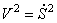
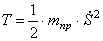
Производные от кинетической энергии
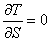
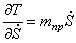
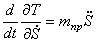
Для определения обобщенной силы Q сообщим системе возможное перемещение 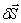
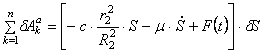
С другой стороны для системы с одной степенью свободы
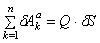
Сравнивая два последних соотношения, получаем
Подставляя производные от кинетической энергии (4.15) и обобщенную силу (4.16) в уравнение Лагранжа, получаем
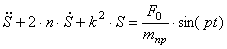
Полученное уравнение (4.18) совпадает с уравнениями (1.25) и (4.11).
3. Анализ колебаний механической системы с одной степенью свободы
3.1. Колебания механической системы при отсутствии сил сопротивления среды
В дифференциальном уравнении движения системы, полученном ранее (1.25), полагаем 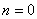
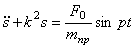
Начальные условия: при 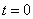
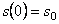
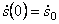
3.1.1. Свободные колебания
Если внешнее возмущение отсутствует (т.е. 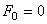
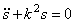
и называется дифференциальным уравнением свободных колебаний, т.е. таких движений системы, которые происходят под действием так называемых восстанавливающих сил. Восстанавливающие силы – это такие силы, каждая из которых стремится вернуть систему в состояние статического равновесия (силы тяжести, упругие силы).
Решение уравнения (5.2) с учетом начальных условий имеет вид:
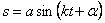
где 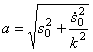
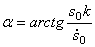
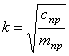
Анализируя решение (5.3) можно сделать следующие выводы:
1. Свободные колебания (рис.5.1) системы с одной степенью свободы представляют собой гармонические колебания.
2. Амплитуда 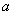
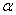
3. Циклическая частота 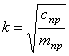
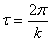
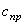
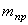
4. Отношения амплитуд колебаний различных точек системы не зависят от начальных условий, так как начальные условия влияют на амплитуды только через множитель 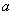
5. Все точки системы всегда находятся в одной фазе, т.е. они одновременно проходят через свои равновесные положения; координаты всех точек одновременно достигают своих максимальных значений.
3.1.2. Вынужденные колебания
При воздействии возмущающей силы 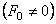
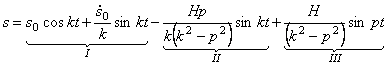
где 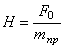
Первые два слагаемых правой части уравнения (5.5):
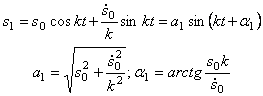
соответствуют свободным колебаниям с частотой 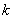
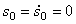
Третье слагаемое в (5.5)
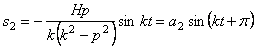
— гармоническое колебание, происходящее с собственной частотой 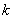
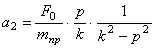
Эти колебания также относятся к свободным колебаниям. Они всегда сопровождают вынужденные колебания при любых начальных условиях, от которых они вообще не зависят.
Их называют сопровождающими колебаниями (рис. 5.2).
Четвертое слагаемое в выражении (4.5):
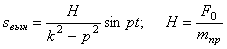
представляет собой вынужденные колебания системы (рис. 5.3).
Таким образом, колебания линейного осциллятора в рассмотренном случае представляют собой линейное наложение трех гармонических колебаний: свободных, сопровождающих и вынужденных (рис. 5.4).
Отметим следующие свойства вынужденных колебаний:
1. Вынужденные колебания происходят с частотой возмущающей силы.
2. Вынужденные колебания не зависят от начальных условий, поэтому для изменения, например, амплитуды (при заданной возмущающей силе) вынужденных колебаний необходимы существенные изменения параметров конструкции: ее жесткости, распределения масс, тогда как в свободных колебаниях для этого достаточно изменить начальные условия.
3. Если 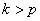
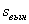
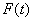
Если 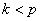
Переписав для этого случая выражение (5.9) в виде:
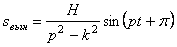
убеждаемся, что при 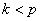
4. Если 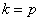
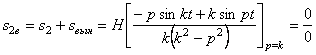
т.е. получим неопределенность, которую можно раскрыть по правилу Лопиталя , заменив дробь в (5.11) пределом
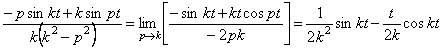
Таким образом, в этом случае общий интеграл (5.5) будет иметь вид:
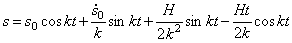
И здесь, как в (5.5) движение осциллятора представляет собой линейное наложение трех колебательных движений, но с одним существенным отличием от (5.5): вынужденные колебания представлены непериодическим слагаемым:
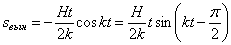
в коэффициенты которого входит время t .
С течением времени он растет по абсолютной величине безгранично, причем вынужденные колебания происходят с возрастающей по линейному закону амплитудой.
Такая ситуация при колебаниях называется резонансом.
5. Если частота вынужденных колебаний не равна частоте свободных колебаний, но близка к ней, то, записав выражение (5.11) в виде:
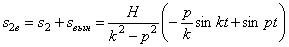
полагаем 
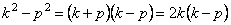
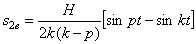
Используя тригонометрическое выражение:
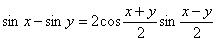

т.е. 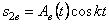
где 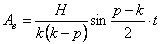
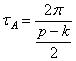
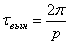
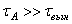
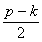
Подобная рассмотренному случаю ситуация представляет собой биение (рис. 5.5).
Таким образом, когда частота вынужденных колебаний весьма близка к частоте свободных (или собственных) колебаний системы, но не равна ей, в колебательной системе возникает биение.
3.2. Колебания механической системы в вязкой среде
Дифференциальное уравнение движения имеет вид (1.25):
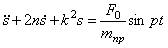
Начальные условия: 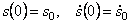
3.2.1. Свободные колебания
Полагая в (5.17) 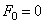
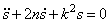
Ограничимся случаем малых сопротивлений и примем 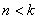
Тогда общее решение однородного уравнения (5.19) с учетом начальных условий можно представить в виде (рис. 5.6):
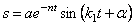
где 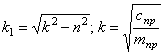
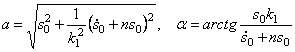
Из закона движения системы (5.20) видно, что в сопротивляющейся среде:
1) свободные колебания являются затухающими;
2) частота затухающих колебаний 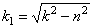
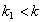
3) амплитуда затухающих колебаний 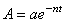
4) период затухающих колебаний 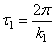
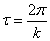
5) отношение любых двух соседних амплитуд: 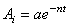
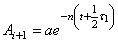
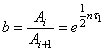
Это отношение называется декрементом затухания. Логарифм этого коэффициента
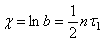
называется логарифмическим декрементом.
Декремент или логарифмический декремент используются для оценки быстроты убывания амплитуды затухающих колебаний.
3.2.2. Вынужденные колебания в сопротивляющейся среде
Дифференциальное уравнение движения в этом случае является неоднородным:
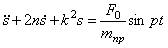
его общее решение имеет вид:
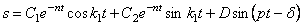
При начальных условиях 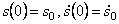
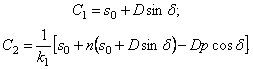
После подстановки постоянных интегрирования (5.27) в общее решение (5.26) получим закон движения механической системы:
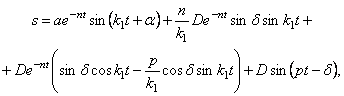
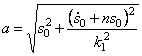
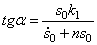
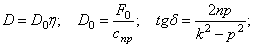
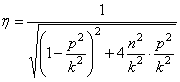
В выражении (5.28) первое слагаемое представляет собой собственные затухающие колебания (рис. 5.6):
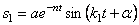
Второе и третье слагаемые в совокупности представляют собой сопровождающие колебания (рис. 5.7):
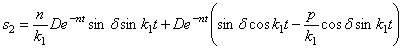
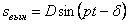
— вынужденные колебания с частотой возмущающей силы (рис. 5.8).
Таким образом, амплитуда вынужденных колебаний при резонансе достигает значительной величины при малых сопротивлениях.
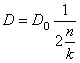
Если 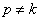
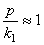
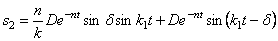
Рассматривая (5.33) и (5.35) совместно и, добавив выражение
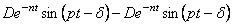
равное нулю, получим закон движения механической системы в виде:
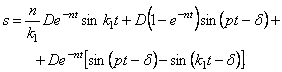
Но выражение в квадратных скобках можно представить так (5.15):
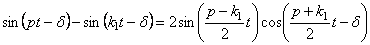
Тогда получим, положив 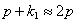

Последнее слагаемое в (5.38) представляет собой колебания биений с затухающей амплитудой
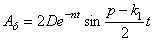
т.е. 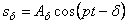
Второе слагаемое в (5.38) – это незатухающие вынужденные колебания
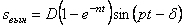
Первое слагаемое в (5.38) – это затухающие сопровождающие колебания
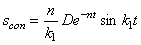
Таким образом, в реальных условиях 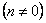
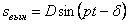
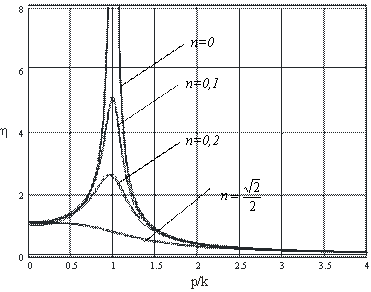
3.3. Коэффициент динамичности
Как было отмечено выше (5.31), коэффициентом динамичности называется отношение максимального динамического отклонения механической системы от положения устойчивого равновесия к статическому отклонению под воздействием силы, равной амплитуде возмущающей силы (рис. 5.10).
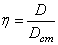
где 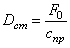
т.е. согласно выражению (5.31):

Максимальное значение 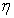
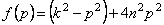
Найдем, при каком значении р функция (5.44) минимальная.
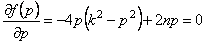
Из (5.45) следует, что
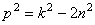
Это возможно, если
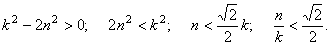
Подставляя (5.46) в (5.43), получаем

При малом значении сопротивления 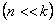
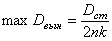
При резонансе 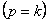
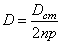
т.е. максимальное значение амплитуды и ее значение при резонансе весьма близки друг к другу (практически одинаковы).
В области, достаточно удаленной от резонанса, при установившемся движении и малом коэффициенте затухания, силами сопротивления можно пренебрегать.
Графические иллюстрации видов колебаний
Рис. 5.1. Собственные колебания
Рис.5.2 Сопровождающие колебания
Рис.5.3 Вынужденные колебания
Рис. 5.4 Результирующие колебания
Рис. 5.5 Биения – результирующие колебания
Колебания в вязкой среде
Рис.5.6. Собственные колебания в вязкой среде
Рис.5.7 Сопровождающие колебания в вязкой среде
Рис. 5.8. Вынужденные колебания
Рис. 5.9 Результирующие колебания в вязкой среде
Рис. 5.10 Коэффициент динамичности
Рис. 5.11. Резонанс ( 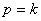
Адрес: Россия, 450071, г.Уфа, почтовый ящик 21
http://mydocx.ru/4-88721.html
http://www.teoretmeh.ru/primerdinamika2.htm