Уравнение с параметром с корнем 11 класс

Задачи с параметрами по теме: Иррациональные уравнения и неравенства.

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

«Актуальность создания школьных служб примирения/медиации в образовательных организациях»

Свидетельство и скидка на обучение каждому участнику

МАОУ ЛИЦЕЙ №44 г. Липецка

Учитель математики: Скорикова Людмила Алексеевна.

Уроки математики в 11 классе

Задачи с параметрами

по теме: Иррациональные уравнения и неравенства.

Углубить знания учащихся по теме иррациональные уравнения и неравенства.

Показать как одна из линий курса математики средней школы “Уравнения и неравенства с параметрами” реализуются в содержании ЕГЭ.

Развивать практические навыки в решении иррациональных неравенств с параметрами.

Развивать логическое мышление, математическую речь, навыки самостоятельной работы, самоконтроля.

Воспитывать познавательный интерес, творческие способности, ответственное отношение. Повысить уровень подготовленности учащихся к сдаче ЕГЭ по математике.

Задачи с параметрами представляют для учащихся наибольшую сложность. Большинство учащихся либо не справляются с такими задачами, либо приводят громоздкое решение без всякой логической стройности. Многие же задачи можно решать различными способами. Решению задач с параметрами в школе уделяется мало внимания. Устранить этот пробел можно на внеклассных занятиях.

Предлагаю занятие по теме: «Иррациональные уравнения и неравенства с параметрами», которое расширит и углубит базовую основу общеобразовательной программы по математике и поможет повысить уровень подготовленности учащихся к сдаче ЕГЭ.

Универсальных указаний по решению задач с параметрами дать нельзя. При решении задач с параметрами приходится рассматривать различные случаи, в зависимости от значений параметров, и методы решения задач различны. Но знание некоторых правил и алгоритмов решения необходимо.

Взяты эти задания из различных источников. Большинство из этих заданий предлагалось на вступительных экзаменах в ВУЗах.

Используются аналитические и графические способы решения уравнений и неравенств.

В конце рассматриваемой темы даются задания для самостоятельной работы.

Данный материал может быть полезным учителям математики, абитуриентам, школьникам.

Иррациональные уравнения и неравенства.

При решении иррациональных уравнений с параметрами пользуются общими формулами. Пусть f и q – некоторые функции, , тогда:

1). , f ≥ 0; q ≥ 0.

2). , f ≥ 0; q > 0.

3). , q ≥ 0.

4). , , q ≠ 0.

5). , fq ≥0.

Применяя эти формулы нужно иметь в виду, что ОДЗ левой и правой частей каждой из них могут быть различными. Для каждой формулы ОДЗ правой части может быть шире ОДЗ левой.

Отсюда следует, что преобразования уравнения с формальным использованием формул «слева-направо» приводят к уравнению, являющемуся следствием исходного. В этом случае могут появиться посторонние корни уравнения.

Преобразование уравнений с формальным использованием данных формул «справа-налево» недопустимы, т.к. возможно сужение ОДЗ исходного уравнения, а следовательно, и потеря корней.

Уравнение вида , равносильно системе:

Решить уравнение .

Заданное уравнение равносильно системе:

=> =>

Находим значения а, при которых

Ответ:

Решить уравнение .

Заданное уравнение равносильно системе:

=>

,

х ₁ , х ₂ являются действительными числами при а ≤ 9/16. При значениях а > 9/16 решений нет.

Удовлетворим неравенства х ≥ а и х ≥ ½.

а) ≥ ½

≥ а

Если а ≤ 9/16, то 8а-5 справедливо при всех допустимых а.

б).

а ≥ ½ (а ≤ 9/16)

Следовательно, х ₂ является решением исходного уравнения при ½ ≤ а ≤ 9/16

Ответ: , если а , если ½ ≤ а ≤ 9/16; нет решений, если а>9/16.

Решить уравнение

ОДЗ: х – а ≥ 0, х ≥ а

Если а = 1, то х ₁ = х ₁ = 1.

Если а ₁ = 1 удовлетворяет условию ОДЗ х ≥ а, т.е. является корнем уравнения.

Если а > 1, то х ₁ = 1 не удовлетворяет условию х ≥ а, т.е. является посторонним корнем.

Ответ: 1) если а ₁ = 1; х ₂ = а; 2) если а ≥ 1, то х = а.

При каких а уравнение имеет один корень?

Корень будет единственным, если а=4; если одно из двух значений (4 и а) является посторонним корнем, а именно х = а. Это произойдет при условии, что х = а не входит в область определения уравнения х ≥ 0, т.е. при а

Ответ: а = 4 или а

Найти минимальное целое положительное значение параметра а, при котором уравнение имеет различные положительные корни.

ах -8 ≥ 0, х ≥ 8/а, х > 0, а > 0

D =

, . А = 17 – минимальное целое число.

Найти все значения параметра а, при которых корни уравнения принадлежат отрезку [2;17].

Пусть

, t ≥ 0, х — 1 = t 2

,

,

1) => => =>

2) => =>

3) => => =>

Ответ: .

Решить уравнение .

х ≥ 2

(х + 1)(х — 2) = а; х 2 – х – 2 = а, х 2 – х – 2 – а = 0.

, .

Множеству х ≥ 2 принадлежит только корень х ₂ .

Ответ: при а ≥ 0 .

Решить уравнение .

. Так как , то m > 0. Пусть у = , тогда х = у 2 + 3, и исходное уравнение равносильно системе уравнений:

т.е. ,

, , .

Ответ: при m m >3 решений нет, при .

Решить уравнение .

Пусть , тогда ,

, , а т.к. t > 0, то ,

, , . ( а > ¼)

х = .

Ответ: х = при а > ¼.

Найти все значения параметра а, при которых уравнение имеет решение.

Если изобразить графики функций и , то очевидно, что они пересекаются (и исходное уравнение имеет решение) при .

При каких значениях а решением неравенства является промежуток [2;18)?

х 2 , т.к. , то

а = 7 – не подходит в ОДЗ.

Решить неравенство , где а – параметр.

При любом значении а, если правая часть х + а – 1

При х ≥ 1 – а равносильная система имеет вид :

=> (*)

Рассмотрим возможные случаи:

Если а > 1, то 1 – а ≤ х . Объединяя с множеством х .

Если а = 1, то х ≥ 1 – решение системы (*). Объединяя с множеством х

Ответ: , если а > 1; , если а ≤ 1.

Решить уравнение

Из данного уравнения следует:

1 – х 2 = х 2 + 2ах + а 2 ,

2х 2 + 2ах + а 2 — 1 = 0.

D /4 = 2 – а 2 . D > 0 при |a| .

Затем если изобразить графики функций и , то видно как меняется количество решений в зависимости от значений а.

Ответ: при нет решений; при и одно решение; при два решения.

1). Решить уравнение .

Ответ: .

2). Найти левый и правый края области значений параметра а, в которой уравнение имеет различные положительные корни.

, х > 0, а ≥ 0.

D = 49 – 4 a 2 > 0

а = -3, 5 не входит в ОДЗ.

3). Решить уравнение .

Данное уравнение равносильно системе:

=>

При а = 2 второе уравнение имеет вид , т.е. .

При а ≠ 2 .

Выясним, при каких значениях а найденное значение х удовлетворяет неравенству х ≥ -1.

.

Ответ: при а ≤ 1/3 и а > 2 ; при 1/3

4). Найти все значения параметра а, при которых корни уравнения принадлежит отрезку [-4;44].

Ответ: .

5). При всех а решить неравенство .

ОДЗ:

а). Если а ≤ 0, то данное неравенство справедливо при всех .

б). Если а > 0, то данное неравенство равносильно системе неравенств.

=> .

Ответ: при ; при .

Уравнения с параметрами
план-конспект урока по алгебре (11 класс) по теме

Урок по теме: «Уравнения с параметрами»

1. Знать, что такое уравнение с параметрами, что значит решить такое уравнение.

2. Уметь решать простейшие уравнения с параметрами.

3. Развивать интерес к заданиям исследовательского характера.

1. Организационная часть.

2. Повторение пройденных тем.

3. Изучение нового материала.

4. Закрепление изученного.

5. Домашнее задание.

Скачать:

Предварительный просмотр:

Урок по теме: «Уравнения с параметрами»

1. Знать, что такое уравнение с параметрами, что значит решить такое уравнение.
2. Уметь решать простейшие уравнения с параметрами.
3. Развивать интерес к заданиям исследовательского характера.

1. Организационная часть.
2. Повторение пройденных тем.
3. Изучение нового материала.
4. Закрепление изученного.
5. Домашнее задание .

1. Организация урока.

Урок начинается с приветствия. Объявляется тема урока и задачи. Нацелить учащихся на важность изучаемого материала не только для подготовки к экзаменам в школе, но и при подготовке к поступлению в вузы.

1) Определите тип уравнения. Сколько корней у него может быть? Решите его.

а) 3х – 6 = 0, 0х = 5, 0х = 0.

ах = в — линейное

а 0 х = — один корень,

а = о, в 0 — нет корней,

а = 0, в = 0 — х – любое число.

б) 2х 2 – 3х + 6 = 0

Измените условие так, чтобы полученное уравнение имело два корня.

ах 2 + вх + с = 0 , а 0 — квадратное

1. Если Д > 0, то 2 корня,

2. Если Д = 0, то 1 корень,

Измените условие так, чтобы полученное уравнение не имело корней.

Измените условие так, чтобы полученное уравнение не имело корней.

х при х > 0,
— х при х

2) Чем отличаются уравнения а х = в и 3х = 6, а х 2 + в х + с = 0 и 2х 2 –3х+6 = 0?

(Ответ учащихся: в первом и третьем уравнениях не числовые коэффициенты).

Учитель: Действительно, в уравнениях а х = в и а х 2 + в х + с = 0 не числовые коэффициенты, а буквенные. Именно такие уравнения и станут предметом нашего изучения на уроке

3. Изучение нового материала.

1) Определение . Уравнение, в котором помимо переменной содержится буквенное выражение, называется уравнением с параметрами.

Примеры: а x + в = 0 (x – переменная, а и в – параметры),

а x 2 + в x + с = 0 (x – переменная, а, в и с – параметры).

2) Чаще всего встречаются две постановки задач.

Первая: для каждого значения параметра найти все решения заданного уравнения.

Вторая: найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.

Пример: ( а – 2)х 2 + 3х – 4 = 0

Первая постановка задачи: решите уравнение. Это значит, что для каждого значения параметра а , необходимо найти решения.

Вторая постановка задачи: при каких значениях параметра а уравнение имеет два различных корня.

Определение. Решить уравнение с параметром – значит, для любого допустимого значения параметра найти множество всех корней заданного уравнения.

1). Простые уравнения без ветвлений:

а) x – а = 0 Ответ: при а ( — , + ) х = а .

б) 5x = а Ответ: при а ( — , + ) х = .

в) x : 2 = а Ответ: при а (- , + ) х = 2 а .

г) [x] = [ а ] Ответ: при а (- , + ) х = ± а .

д) x 3 = а Ответ: при а (- , + ) х = .

2). Простые уравнения с ветвлениями:

а) а x = 10 Ответ: при а 0 х = , при а = 0 решений нет.

б) 0x = а Ответ: при а 0 корней нет, при а = 0 х – любое число.

в) [х] = а Ответ: при а а = 0 х = 0, при а > о х = а.

г) ( а 2 – 4)x = а 2 + а – 6

Решение г). Если а 2 – 4 0, т.е. а ± 2, то х = .

При а = -2 уравнение имеет вид: 0х = -4, т.е. не имеет корней.

При а = 2 исходное уравнение принимает вид: 0х = 0, т.е. х – любое число.

Ответ: при а ± 2 х = ,

при а = — 2 корней нет,

при а = 2 х – любое число.

(Обратить внимание учащихся на тот факт, что при решении данного уравнения получили исключение для параметра. В таких случаях необходимо делать проверку (испытание) для каждого исключения: подставить значение параметра в исходное уравнение и решить его).

Решение: х 2, тогда а = х – 2 или х = а + 2.

Найдем а , при котором х = 2

Итак, при а = 0 х = 2, но это посторонний корень.

Ответ: при а = 0 корней нет, при а 0 х = а + 2.

2) ( а – 2)х 2 + 3х – 4 = 0.

(Обратить внимание учащихся на то, что в ходе решения уравнения 1) появилось исключение для х. В таком случае необходимо найти значение параметра, при котором есть исключение для переменной).

Повторить основные этапы решения уравнений с параметрами.

Домашнее задание: опорный конспект и решение уравнений (примерный набор заданий – карточки).

11 класс. Задачи с параметром.

» Всякая задача кажется очень простой, после того, как Вам ее растолкуют.»

Просмотр содержимого документа
«11 класс. Задачи с параметром.»

Разработка уроков-консультаций в 11 классе.

«Задачи с параметром».

Подготовила Л.И. Гоптарь.

Знать, что такое уравнение с параметрами, что значит решить такое уравнение.

Уметь решать простейшие уравнения с параметрами.

Развивать интерес к заданиям исследовательского характера.

1) Определите тип уравнения. Сколько корней у него может быть? Решите его.

а) 2х – 6 = 0, 0х = 6, 0х = 0.

Повторим основные сведения:

ах = в — линейное

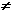
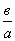
а 0 х = — один корень,

а = о, в 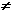0 — нет корней,

а = 0, в = 0 — х – любое число.

б) Определите количество корней 2х 2 – 3х + 8 = 0 (т.к. Д

Измените условие так, чтобы полученное уравнение имело два корня.

Повторим основные сведения:

ах 2 + вх + с = 0 , а 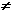0 — квадратное

1. Если Д 0, то 2 корня,

2. Если Д = 0, то 1 корень,

в) 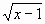= 5

Измените условие так, чтобы полученное уравнение не имело корней.

Измените условие так, чтобы полученное уравнение не имело корней.

2) Чем отличаются уравнения ах = 6 и 3х = 6, ах 2 + 7х + с = 0 и 2х 2 –3х+6 = 0?

(Ответ учащихся: в первом и третьем уравнениях не числовые коэффициенты).

Действительно, в уравнениях ах = 6 и ах 2 + 7х + с = 0 не числовые коэффициенты, а буквенные. Именно такие уравнения и станут предметом нашего изучения на уроке.

3. Изучение нового материала.

1) Определение. Уравнение, в котором помимо переменной содержится буквенное выражение, называется уравнением с параметрами.

Примеры: аx + в = 0 (x – переменная, а и в – параметры),

аx 2 + вx + с = 0 (x – переменная, а, в и с – параметры).

2) Чаще всего встречаются две постановки задач.

Первая: для каждого значения параметра найти все решения заданного уравнения.

Вторая: найти все значения параметра, при каждом из которых решения уравнения удовлетворяют заданным условиям.

Определение. Решить уравнение с параметром – значит, для любого допустимого значения параметра найти множество всех корней заданного уравнения.

Решение уравнений. (Учащиеся привлекаются к поиску ответов).

1). Простые уравнения без ветвлений:

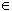
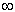
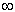
а) x – а = 0 Ответ: приа ( — , + ) х = а.

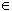
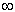
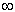
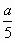
б) 5x = а Ответ: при а ( — , + ) х = .

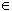
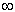
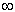
в) x : 8 = а Ответ: при а (- , + ) х = 8а.

2). Простые уравнения с ветвлениями:

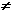
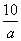
а) аx = 10 Ответ: при а 0 х = , при а = 0 решений нет.

б) 0x = а Ответ: при а 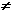0 корней нет, при а = 0, х – любое число.

в) [х] = а Ответ: приаа = 0 х = 0, при а 0, х = а.

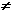
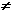
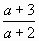
Решение г). Если а 2 – 4 0, т.е. а ± 2, то х = .

Приа = -2 уравнение имеет вид: 0х = -4, т.е. не имеет корней.

Приа = 2 исходное уравнение принимает вид: 0х = 0, т.е. х – любое число.

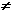
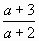
Ответ: приа ± 2 х = ,

приа = — 2 корней нет,

приа = 2 х – любое число.

4. Закрепление. (Коллективный поиск решения, оформление решения в тетрадях учащихся).

1) Решить уравнение а (а – 1) = а – 1.

Решение. Перед нами линейное уравнение, имеющее смысл при всех допустимых значениях а. Будем решать его «как обычно»: делим обе части уравнения на коэффициент при неизвестном. Но всегда ли возможно деление?(Нет.Делить на ноль нельзя.)

Придется рассмотреть отдельно случай, когда коэффициент при неизвестном равен 0. Получим:

а = 1, тогда уравнение примет вид 0·х = 0, где х – любое число;

а = 0, тогда 0∙х = — 1 – уравнение корней не имеет;

а 0, а 1, тогда а (а – 1)·х = а – 1 х = .

Ответ: 1) если а 0, а 1, то х = ;

2) если а = 1, то х – любое число;

3) если а = 0, то корней нет.

2) Решить уравнение (а – 1)х 2 + 2 (2а – 1)х + 4 а + 3 = 0.

Решение. Рассмотрим два случая:

а = 1 – получим линейное уравнение 2х + 7 = 0, откуда х = — 3,5;

а 1 – получим квадратное уравнение.

Рассмотрим дискриминант: D = (2а – 1) 2 – (а – 1)(4а + 3) = — 3а + 4.

Далее, если а , то D

Если же а , то х_1,2 = .

Ответ: 1) если а , то корней нет;

2) если а = 1, то х = — 3,5;

3) если а и а 1, то х_1,2 = .

3)При каких значениях а уравнение sin 2x – asinx=0 имеет решения для каждого а, указать их?

2sin x cos x – a sin x = 0;

sin x (2 cos x-a) = 0

Sin x = 0 или 2cos x – a = 0

x=πn при любом значении а

cosx = a/2, есть решения, если |а|/2≤1, -2≤а≤2

x = ± arccosa/2 + 2πm, m € Z

Итак, при а € (-∞;+ ∞), х = πn, n € Z

при а € [-2;2], х = ± arcosa/2 + 2πm, m € Z

Ответ: а € (-∞;+ ∞), х = πn, n € Z

а € [-2;2], х = ± arcos a/2 + 2πm, m € Z

5.Примеры заданий на исследование уравнений.

Особенно часто встречаются задачи на расположение корней квадратного уравнения. При их решении хорошо «работают» графические иллюстрации. Расположение корней относительно заданных точек плоскостью определяется направлением ветвей соответствующей параболы, координатами вершины, а также значениями в заданных точках.

1) При каких значениях параметра а уравнение (а 2 + а + 1)х 2 + (2а – 3)х + а – 5 = 0 имеет два корня, один из которых больше 1, а другой меньше 1?

Решение. Пусть f(х) = (а 2 + а + 1)х 2 + (2а – 3)х + а – 5. Так как а 2 + а + 1 0, то для квадратичной функции f(х) условие задачи может выполняться только при условии f (1)

Решая неравенство f(1) = а 2 + 4а – 7 .

2) При каких значениях параметра m корни уравнения (m – 1)х 2 – 2mх + m + 3 = 0 положительны?

Решение. Пусть f(х) = (m-1)х 2 — 2 mх + m + 3 тогда:

1) если, m = 1,то -2х + 4=0, х= 2- корень положителен;

2) если m 1, то с помощью рисунка можно получить следующие соотношения:

Рассмотрим 2 случая:

2) если m -1 0,( рис. б)), тогда из 2 и 3 неравенств последней системы получим, что m 1, т.е. окончательно 1,5 m 1;

6.Рассмотрим задачи на установления числа корней уравнения.

При каких значениях а уравнение имеет единственный корень?

Решение. В силу свойств показательной функции данное показательное уравнение равносильно уравнению

т.е. исходное уравнение имеет единственный корень тогда и только тогда, когда уравнение

(а-1)х² +2(а+3)х + а +2 = 0; имеет единственный корень.

При а ≠ 1 квадратное уравнение имеет один корень если Д=0. Д= 5а + 11 ; а=-2.2

Итак, исходное показательное уравнение имеет один корень только при а = 1 и

Пример 1. При каких значениях параметра, а уравнение 2 cos 2 x – (2а + 9)cosx + 9а = 0 не имеет корней.

Решение. Пусть у = cosх, тогда исходное уравнение примет вид 2у 2 – (2 а + 9)у + 9а = 0, корни которого у₁ = а, у₂ = 4,5.

Уравнение cosх = 4,5 корней не имеет, а уравнение cosх = а не имеет корней, если 1.

Задачи на нахождение общего корня двух уравнений.

Пример 1. При каких значениях параметра а уравнение х 2 + 3х + 7а -21 =0 и х 2 +6х +5а -6 =0 имеют общий корень?

Решение. Исключим параметр а из полученной системы.

Для этого первое уравнение умножим на (-5), второе умножим на7, а результаты сложим.

Подставим корни в одно из уравнений и найдем значение параметра а.

Пример 2. При каких значениях параметра а уравнение х 2 – ах + 2 = 0 и 3х 2 + (а — 9)х+ 3=0 равносильны?

Решение. Как известно уравнения равносильны, если множество их корней совпадают. Рассмотрим 2 случая.

1) Уравнения не имеют корней (множество корней пусто). Тогда их дискриминанты отрицательны:

Система неравенств решений не имеет.

2) Уравнения имеют общие корни. Тогда

Следовательно, данные уравнения могут иметь общие корни только приа = 3 или а = .

7.Задачи с применением геометрической интерпретации.

Решение задач с параметрами может существенно облегчить использование графиков.

Пример 1. Укажите количество корней в зависимости от параметра а: .

Построим график функции а = .
Количество корней можно увидеть на рисунке:

Ответ: 1) еслиа , то корней нет;

2) еслиа = 0,а 4, то 2 корня

4) еслиа = 4, то 3 корня

8.Рефлексия. Итог урока. Оценки.

Самостоятельную работу можно предложить учащимся в классе, как и в качестве дополнительной работы по теме на последующих уроках…