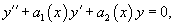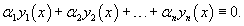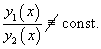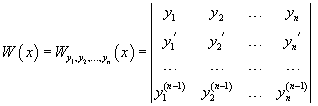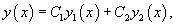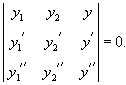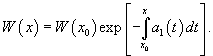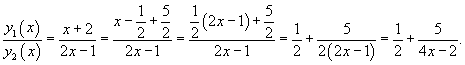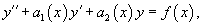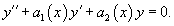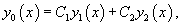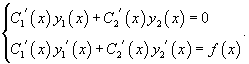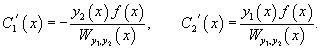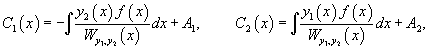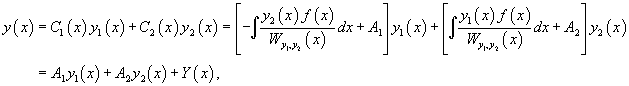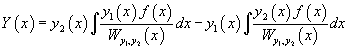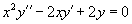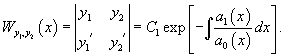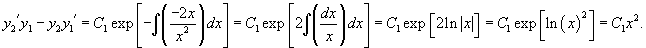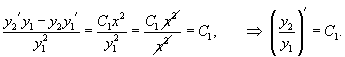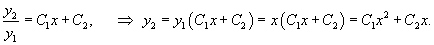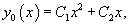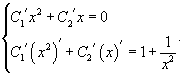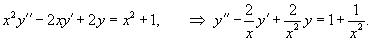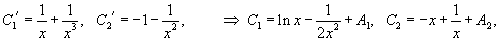Уравнение с переменными коэффициентами на постоянные

Уравнение с переменными коэффициентами на постоянные

Если же это тождество выполняется лишь при , то указанные функции , , . называются линейно независимыми на отрезке .

Для случая двух функций критерий линейной независимости можно записать в более простом виде: Функции , будут линейно независимыми на отрезке , если их отношение на данном отрезке тождественно не равно постоянной:

В противном случае, при 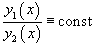, эти функции будут линейно зависимыми .

Пусть n функций , , . имеют производные порядка. Определитель

называется определителем Вронского или вронскианом для указанной системы функций.

Теорема . Если система функций , , . линейна зависима на отрезке , то ее определитель Вронского тождественно равен нулю на этом отрезке.

Отсюда следует, что если определитель отличен от нуля хотя бы в одной точке отрезка , то функции , , . будут линейно независимыми. Это свойство определителя Вронского позволяет выяснить, являются ли найденные решения однородного дифференциального уравнения линейно независимыми.

Совокупность двух линейно независимых частных решений линейного однородного дифференциального уравнения второго порядка образует его фундаментальную систему решений .

Если , − фундаментальная система решений, то общее решение уравнения второго порядка представляется в виде

где , − произвольные постоянные.

Заметим, что по заданной фундаментальной системе решений , можно построить соответствующее однородное дифференциальное уравнение. Для случая второго порядка такое уравнение выражается через определитель в виде:

Итак, как указано выше, общее решение однородного дифференциального уравнения второго порядка является линейной комбинацией двух линейно независимых частных решений , этого уравнения.

Очевидно, что частные решения зависят от коэффициентов дифференциального уравнения. Формула Лиувилля-Остроградского устанавливает связь между вронскианом , построенном на базе частных решений , , и коэффициентом в дифференциальном уравнении.

Пусть − определитель Вронского решений , линейного однородного дифференциального уравнения 2-го порядка

К сожалению, общего метода отыскания частного решения не существует. Обычно это можно сделать путем подбора.

Если известно частное решение линейного однородного уравнения второго порядка, то его можно преобразовать к линейному уравнению первого порядка с помощью подстановки и последующей замены .

Другой способ понижения порядка основан на использовании формулы Лиувилля-Остроградского. Здесь также одно частное решение должно быть известно. Соответствующие примеры разобраны ниже.

где , и − непрерывные функции на отрезке .

Соответствующее однородное уравнение записывается в виде

Метод вариации постоянных (или метод Лагранжа) используется для построения общего решения неоднородного уравнения, когда известно общее решение ассоциированного с ним однородного уравнения.

Пусть общее решение однородного уравнения 2-го порядка выражается через фундаментальную систему решений и :

где C₁, C₂ − произвольные постоянные. Идея данного метода состоит в том, что вместо постоянных C₁ и C₂рассматриваются функции и , которые подбираются таким образом, чтобы решение удовлетворяло неоднородному уравнению.

Производные неизвестных функций и можно определить из системы уравнений

Применяя метод вариации параметров, важно помнить, что функция должна соответствовать дифференциальному уравнению, приведенному к стандартному виду, т.е. коэффициент перед старшей производной должен быть равен 1.

Далее, зная производные и , можно найти и сами функции и :

Тогда общее решение исходного неоднородного уравнения будет выражаться формулой

Теперь воспользуемся методом вариации постоянных и построим общее решение неоднородного уравнения. Будем рассматривать параметры C₁ и C₂ как функции от переменной x. Производные этих функций определяются из системы уравнений

В результате получаем общее решение неоднородного уравнения в виде

ЛДУ с переменными коэффициентами. Метод Лагранжа

Линейные дифференциальные уравнения с переменные коэффициентами

Если известно частное решение уравнения

то его порядок можно понизить на единицу (не нарушая линейности уравнения), полагая , где — новая неизвестная функция, а затем делая замену (можно непосредственно делать замену ).

Если известно частных линейно независимых решений уравнения (32), то порядок уравнения может быть понижен на единиц.

Общее решение уравнения

есть сумма какого-нибудь его частного решения и общего решения соответствующего однородного уравнения (32).

Если известна фундаментальная система соответствующего однородного уравнения (32), то общее решение неоднородного уравнения (33) может быть найдено методом вариации постоянных ( метод Лагранжа ).

Общее решение уравнения (32) имеет вид

где — произвольные постоянные.

Будем искать решение уравнения (33) в виде

где — некоторые пока неизвестные функции от . Для их определения получаем систему

Разрешая эту систему относительно , получаем

где — произвольные постоянные. Внося найденные значения в (34), получаем общее решения уравнения (33).

В частности, для уравнения второго порядка

Решая (36) относительно и , получаем

где и — постоянные интегрирования.

Замечание. Для уравнения , где , система (36) будет выглядеть так:

Пример 1. Найти общее решение уравнения , если есть его частное решение.

Решение. Положим , где — новая неизвестная функция от , тогда

Подставляя в данное уравнение, получаем

Но так как есть частное решение данного уравнения, то , поэтому имеем

Но , а значит , и уравнение (37) примет вид

Перепишем его в виде . Отсюда имеем , откуда

Интегрируя это уравнение, найдем и, следовательно, общее решение данного уравнения будет

Пример 2. Найти общее решение уравнения .

Решение. Общее решение соответствующего однородного уравнения имеет вид (см. пример 1)

и следовательно, его фундаментальная система решений будет

Будем искать общее решение данного уравнения методом вариации произвольных постоянных:

где — постоянные неизвестные функции от , подлежащие определению. Для их нахождения составим следующую систему:

Отсюда находим: . Интегрируя, получаем

Подставляя эти значения и в выражение для , найдем общее решение данного уравнения

Пример 3. Решить уравнение .

Решение. Соответствующее однородное уравнение будет . Его характеристическое уравнение имеет мнимые корни , и общее решение однородного уравнения имеет вид

Общее решение исходного уравнения ищем в виде

где и — неизвестные функции от . Для их нахождения составим систему

Разрешаем эту систему относительно и :

Подставляя выражения и в (38), получаем общее решение данного уравнения

Здесь есть частное решение исходного неоднородного уравнения.

Пример 4. Зная фундаментальную систему решений соответствующего однородного уравнения, найти частное решение уравнения

Решение. Применяя метод вариации постоянных, находим общее решение уравнения (39):

При первые два слагаемых правой части (40) стремятся к бесконечности, причем при любых , неравных нулю одновременно, функция есть бесконечно большая функция при . Третье слагаемое правой части (40) имеет пределом ноль при , что легко установить с помощью правила Лопиталя. Таким образом, функция , которая получается из (40) при и , будет решением уравнения (39), удовлетворяющим условию .

Составление дифференциального уравнения по заданной фундаментальной системе решений

Рассмотрим линейно независимую на отрезке систему функций

имеющих все производные до n-го порядка включительно. Тогда уравнение

где — неизвестная функция, будет линейным дифференциальным уравнением, для которого, как нетрудно видеть, функции составляют фундаментальную систему решений. Коэффициент при в (42) есть определитель Вронского системы (41). Те точки, в которых этот определитель обращается в ноль, будут особыми точками построенного уравнения — в этих точках обращается в ноль коэффициент при старшей производной .

Пример 1. Составить дифференциальное уравнение, для которого образуют фундаментальную систему решений.

Решение. Применяя формулу (42), получаем

Раскрывая определитель в левой части (43) по элементам третьего столбца, будем иметь . Это и есть искомое дифференциальное уравнение.

Пример 2. Составить дифференциальное уравнение, для которого функции фундаментальную систему решений образуют функции .

Решение. Составим уравнение вида (42):

Раскрывая последний определитель по элементам 3-го столбца, будем иметь

В этом примере определитель Вронского обращается в ноль при . Это не противоречит общей теории, в силу которой определитель Вронского фундаментальной системы решений линейного однородного дифференциального уравнения

с непрерывными на отрезке коэффициентами не обращается в ноль ни в одной точке отрезка . Записав уравнение (44) в виде

видим, что коэффициент при терпит разрыв при , так что в точке непрерывность коэффициентов уравнения (45) нарушается.

Разные задачи

Пусть — фундаментальная система линейного однородного уравнения

Тогда имеет место формула Остроградского–Лиувилля

где — определитель Вронского, а — любое значение из отрезка , на котором непрерывны коэффициенты уравнения.

Пример 1. Показать, что линейное дифференциальное уравнение имеет решение вида , где — некоторый многочлен. Показать, что второе решение этого уравнения имеет вид , где — также многочлен.

Решение. Будем искать решение в виде многочлена, например, первой степени: . Подставляя в уравнение, найдем, что . Пусть , тогда ;. таким образом, многочлен будет решением данного уравнения. Перепишем данное уравнение в виде

Пусть — второе частное решение данного уравнения, линейно независимое с первым. Находим определитель Вронского системы решений

здесь . Применяя формулу Остроградского–Лиувилля, будем иметь

где — любое значение , причем , или ; здесь . Для нахождения получили линейное дифференциальное уравнение первого порядка. Деля обе части этого уравнения на , приведем его к виду

Виды дифференциальных уравнений

Существует целый ряд задач, в которых установить прямую связь между величинами, применяемыми для описания процесса, не получается. Единственное, что можно сделать, это получить равенство, запись которого включает производные исследуемых функций, и решить его. Решение дифференциального уравнения позволяет установить непосредственную связь между величинами.

В этом разделе мы займемся разбором решений дифференциальных уравнений, неизвестная функция в которых является функцией одной переменной. Мы построили теоретическую часть таким образом, чтобы даже человек с нулевым представлением о дифференциальных уравнениях мог без труда получить необходимые знания и справиться с приведенными задачами.

Если какие-то термины окажутся для вас новыми, обратитесь к разделу «Определения и понятия теории дифференциальных уравнений». А тем временем перейдем к рассмотрению вопроса о видах дифференциальных уравнений.

Для каждого из видов дифференциальных уравнений применяется свой метод решения. В этом разделе мы рассмотрим все эти методы, приведем примеры с подробными разборами решения. После ознакомления с темой вам необходимо будет определять вид дифференциального уравнения и выбирать наиболее подходящий из методов решения поставленной задачи.

Возможно, прежде чем приступить к решению дифференциальных уравнений, вам придется освежить в памяти такие темы как «Методы интегрирования» и «Неопределенные интегралы».

Начнем ознакомление с темой мы с видов обыкновенных дифференциальных уравнений 1 -го порядка. Эти уравнения могут быть разрешены относительно производной. Затем перейдем в ОДУ 2 -го и высших порядков. Также мы уделим внимание системам дифференциальных уравнений.

Напомним, что y ‘ = d x d y , если y является функцией аргумента x .

Дифференциальные уравнения первого порядка

Простейшие дифференциальные уравнения первого порядка вида y ‘ = f ( x )

Начнем с примеров таких уравнений.

y ‘ = 0 , y ‘ = x + e x — 1 , y ‘ = 2 x x 2 — 7 3

Оптимальным для решения дифференциальных уравнений f ( x ) · y ‘ = g ( x ) является метод деления обеих частей на f ( x ) . Решение относительно производной позволяет нам прийти к уравнению вида y ‘ = g ( x ) f ( x ) . Оно является эквивалентом исходного уравнения при f ( x ) ≠ 0 .

Приведем примеры подобных дифференциальных уравнений:

e x · y ‘ = 2 x + 1 , ( x + 2 ) · y ‘ = 1

Мы можем получить ряд дополнительных решений в тех случаях, когда существуют значения аргумента х , при которых функции f ( x ) и g ( x ) одновременно обращаются в 0 . В качестве дополнительного решения в уравнениях f ( x ) · y ‘ = g ( x ) при заданных значениях аргумента может выступать любая функция, определенная для заданного значения х .

Наличие дополнительных решений возможно для дифференциальных уравнений x · y ‘ = sin x , ( x 2 — x ) · y ‘ = ln ( 2 x 2 — 1 )

Ознакомиться с теоретической частью и примерами решения задач таких уравнений вы можете в разделе «Простейшие дифференциальные уравнения 1 -го порядка».

Дифференциальные уравнения с разделяющимися переменными вида f 1 ( y ) · g 1 ( x ) d y = f 2 ( y ) · g 2 ( x ) d x или f 1 ( y ) · g 1 ( x ) · y ‘ = f 2 ( y ) · g 2 ( x )

Поговорим теперь об уравнениях с разделенными переменными, которые имеют вид f ( y ) d y = g ( x ) d x . Как следует из названия, к данному виду дифференциальных уравнений относятся выражения, которые содержат переменные х и у , разделенные знаком равенства. Переменные находятся в разных частях уравнения, по обе стороны от знака равенства.

Решить уравнения с разделенными переменными можно путем интегрирования обеих его частей: ∫ f ( y ) d y = ∫ f ( x ) d x

К числу дифференциальных уравнений с разделенными переменными можно отнести следующие из них:

y 2 3 d y = sin x d x , e y d y = ( x + sin 2 x ) d x

Для того, чтобы прийти от ДУ с разделяющимися переменными к ДУ с разделенными переменными, необходимо разделить обе части уравнения на произведение f 2 ( y ) ⋅ g 1 ( x ) . Так мы придем к уравнению f 1 ( y ) f 2 ( y ) d y = g 2 ( x ) g 1 ( x ) d x . Преобразование можно будет считать эквивалентным в том случае, если одновременно f 2 ( y ) ≠ 0 и g 1 ( x ) ≠ 0 . Если хоть одно из условий не будет соблюдаться, мы можем потерять часть решений.

В качестве примеров дифференциальных уравнений с разделяющимися переменными можно привести следующие из них: d y d x = y · ( x 2 + e x ) , ( y 2 + a r c cos y ) · sin x · y ‘ = cos x y .

К уравнениям с разделяющимися переменными мы можем прийти от ряда дифференциальных уравнений других видов путем замены переменных. Например, мы можем подставить в исходное уравнение z = a x + b y . Это позволит нам перейти к дифференциальному уравнению с разделяющимися переменными от дифференциального уравнения вида y ‘ = f ( a x + b y ) , a , b ∈ R .

Подставив z = 2 x + 3 y в уравнение y ‘ = 1 e 2 x + 3 y получаем d z d x = 3 + 2 e z e z .

Заменив z = x y или z = y x в выражениях y ‘ = f x y или y ‘ = f y x , мы переходим к уравнениям с разделяющимися переменными.

Если произвести замену z = y x в исходном уравнении y ‘ = y x · ln y x + 1 , получаем x · d z d x = z · ln z .

В ряде случаев прежде, чем производить замену, необходимо произвести преобразования исходного уравнения.

Предположим, что в условии задачи нам дано уравнение y ‘ = y 2 — x 2 2 x y . Нам необходимо привести его к виду y ‘ = f x y или y ‘ = f y x . Для этого нам нужно разделить числитель и знаменатель правой части исходного выражения на x 2 или y 2 .

Нам дано уравнение y ‘ = f a 1 x + b 1 y + c 1 a 2 x + b 2 y + c 2 , a 1 , b 1 , c 1 , a 2 , b 2 , c 2 ∈ R .

Для того, чтобы привести исходное уравнение к виду y ‘ = f x y или y ‘ = f y x , нам необходимо ввести новые переменные u = x — x 1 v = y — y 1 , где ( x 1 ; y 1 ) является решением системы уравнений a 1 x + b 1 y + c 1 = 0 a 2 x + b 2 y + c 2 = 0

Введение новых переменных u = x — 1 v = y — 2 в исходное уравнение y ‘ = 5 x — y — 3 3 x + 2 y — 7 позволяет нам получить уравнение вида d v d u = 5 u — v 3 u + 2 v .

Теперь выполним деление числителя и знаменателя правой части уравнения на u . Также примем, что z = u v . Получаем дифференциальное уравнение с разделяющимися переменными u · d z d u = 5 — 4 z — 2 z 2 3 + 2 z .

Подробный разбор теории и алгоритмов решения задач мы привели в разделе «Дифференциальные уравнения с разделяющимися переменными».

Линейные неоднородные дифференциальные уравнения первого порядка y ‘ + P ( x ) · y = Q ( x )

Приведем примеры таких уравнений.

К числу линейных неоднородных дифференциальных уравнений 1 -го порядка относятся:

y ‘ — 2 x y 1 + x 2 = 1 + x 2 ; y ‘ — x y = — ( 1 + x ) e — x

Для решения уравнений этого вида применяется метод вариации произвольной постоянной. Также мы можем представить искомую функцию у в виде произведения y ( x ) = u ( x ) v ( x ) . Алгоритмы применения обоих методов мы привели в разделе «Линейные неоднородные дифференциальные уравнения первого порядка».

Дифференциальное уравнение Бернулли y ‘ + P ( x ) y = Q ( x ) y a

Приведем примеры подобных уравнений.

К числу дифференциальных уравнений Бернулли можно отнести:

y ‘ + x y = ( 1 + x ) e — x y 2 3 ; y ‘ + y x 2 + 1 = a r c t g x x 2 + 1 · y 2

Для решения уравнений этого вида можно применить метод подстановки z = y 1 — a , которая выполняется для того, чтобы свести исходное уравнение к линейному дифференциальному уравнению 1 -го порядка. Также применим метод представления функции у в качестве y ( x ) = u ( x ) v ( x ) .

Алгоритм применения обоих методов приведен в разделе «Дифференциальное уравнение Бернулли». Там же можно найти подробный разбор решения примеров по теме.

Уравнения в полных дифференциалах P ( x , y ) d x + Q ( x , y ) d y = 0

Если для любых значений x и y выполняется ∂ P ( x , y ) ∂ y = ∂ Q ( x , y ) ∂ x , то этого условия необходимо и достаточно, чтобы выражение P ( x , y ) d x + Q ( x , y ) d y представляло собой полный дифференциал некоторой функции U ( x , y ) = 0 , то есть, d U ( x , y ) = P ( x , y ) d x + Q ( x , y ) d y . Таким образом, задача сводится к восстановлению функции U ( x , y ) = 0 по ее полному дифференциалу.

Выражение, расположенное в левой части записи уравнения ( x 2 — y 2 ) d x — 2 x y d y = 0 представляет собой полный дифференциал функции x 3 3 — x y 2 + C = 0

Для более подробного ознакомления с теорией и алгоритмами решения примеров можно обратиться к разделу «Уравнения в полных дифференциалах».

Дифференциальные уравнения второго порядка

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = 0 , p , q ∈ R

Линейное однородное дифференциальное уравнение с постоянными коэффициентами обычно решается достаточно просто. Нам необходимо найти корни характеристического уравнения k 2 + p k + q = 0 . Здесь возможны три варианта в зависимости от различных p и q :

• действительные и различающиеся корни характеристического уравнения k 1 ≠ k 2 , k 1 , k 2 ∈ R ;
• действительные и совпадающие k 1 = k 2 = k , k ∈ R ;
• комплексно сопряженные k 1 = α + i · β , k 2 = α — i · β .

Значения корней характеристического уравнения определяет, как будет записано общее решение дифференциального уравнения. Возможные варианты:

• y = C 1 e k 1 x + C 2 e k 2 x ;
• y = C 1 e k x + C 2 x e k x ;
• y = e a · x · ( C 1 cos β x + C 2 sin β x ) .

Пример 13

Предположим, что у нас есть линейное однородное дифференциальное уравнение 2 -го порядка с постоянными коэффициентами y ‘ ‘ + 3 y ‘ = 0 . Найдем корни характеристического уравнения k 2 + 3 k = 0 . Это действительные и различные k 1 = — 3 и k 2 = 0 . Это значит, что общее решение исходного уравнения будет иметь вид:

y = C 1 e k 1 x + C 2 e k 2 x ⇔ y = C 1 e — 3 x + C 2 e 0 x ⇔ y = C 1 e — 3 x + C 2

Восполнить пробелы в теоретической части и посмотреть подробный разбор примеров по теме можно в статье «Линейные однородные дифференциальные уравнения 2 -го порядка с постоянными коэффициентами».

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами y ‘ ‘ + p y ‘ + q y = f ( x ) , p , q ∈ R

Основным способом решение уравнений данного вида является нахождение суммы общего решения y 0 , которое соответствует линейному однородному дифференциальному уравнению y ‘ ‘ + p y ‘ + q y = 0 , и частного решения y

исходного уравнения. Получаем: y = y 0 + y

Способ нахождения y 0 мы рассмотрели в предыдущем пункте. Найти частное решение y

мы можем методом неопределенных коэффициентов при определенном виде функции f ( x ) , которая расположена в правой части записи исходного выражения. Также применим метод вариации произвольных постоянных.

К числу линейных неоднородных дифференциальных уравнений 2 -го порядка с постоянными коэффициентами относятся:

y ‘ ‘ — 2 y ‘ = ( x 2 + 1 ) e x ; y ‘ ‘ + 36 y = 24 sin ( 6 x ) — 12 cos ( 6 x ) + 36 e 6 x

Теоретические выкладки и подробный разбор примеров по теме можно найти в разделе «ЛНДУ 2 -го порядка с постоянными коэффициентами».

Линейные однородные дифференциальные уравнения (ЛОДУ) y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 и линейные неоднородные дифференциальные уравнения (ЛНДУ) второго порядка y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x )

Линейные однородные и неоднородные дифференциальные уравнения и постоянными коэффициентами являются частными случаями дифференциальных уравнений этого вида.

На некотором отрезке [ a ; b ] общее решение линейного однородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = 0 представлено линейной комбинацией двух линейно независимых частных решений y 1 и y 2 этого уравнения, то есть, y = C 1 y 1 + C 2 y 2 .

Частные решения мы можем выбрать из систем независимых функций:

1 ) 1 , x , x 2 , . . . , x n 2 ) e k 1 x , e k 2 x , . . . , e k n x 3 ) e k 1 x , x · e k 1 x , . . . , x n 1 · e k 1 x , e k 2 x , x · e k 2 x , . . . , x n 2 · e k 2 x , . . . e k p x , x · e k p x , . . . , x n p · e k p x 4 ) 1 , c h x , s h x

Однако существуют примеру уравнений, для которых частные решения не могут быть представлены в таком виде.

Возьмем для примера линейное однородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = 0 .

Общее решение линейного неоднородного дифференциального уравнения y ‘ ‘ + p ( x ) · y ‘ + q ( x ) · y = f ( x ) мы можем найти в виде суммы y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

частное решение исходного дифференциального уравнения. Найти y 0 можно описанным выше способом. Определить y

нам поможет метод вариации произвольных постоянных.

Возьмем для примера линейное неоднородное дифференциальное уравнение x y ‘ ‘ — x y ‘ + y = x 2 + 1 .

Более подробно этот раздел освещен на странице «Линейные дифференциальные уравнения второго порядка».

Дифференциальные уравнения высших порядков

Дифференциальные уравнения, допускающие понижение порядка

Мы можем провести замену y ( k ) = p ( x ) для того, чтобы понизить порядок исходного дифференциального уравнения F ( x , y ( k ) , y ( k + 1 ) , . . . , y ( n ) ) = 0 , которое не содержит искомой функции и ее производных до k — 1 порядка.

В этом случае y ( k + 1 ) = p ‘ ( x ) , y ( k + 2 ) = p ‘ ‘ ( x ) , . . . , y ( n ) = p ( n — k ) ( x ) , и исходное дифференциальное уравнение сведется к F 1 ( x , p , p ‘ , . . . , p ( n — k ) ) = 0 . После нахождения его решения p ( x ) останется вернуться к замене y ( k ) = p ( x ) и определить неизвестную функцию y .

Дифференциальное уравнение y ‘ ‘ ‘ x ln ( x ) = y ‘ ‘ после замены y ‘ ‘ = p ( x ) станет уравнением с разделяющимися переменными y ‘ ‘ = p ( x ) , и его порядок с третьего понизится до первого.

В уравнении, которое не содержит аргумента х и имеет вид F ( y , y ‘ , y ‘ ‘ , . . . , y ( n ) ) = 0 , порядок может быть заменен на единицу следующим образом: необходимо провести замену d y d x = p ( y ) , где p ( y ( x ) ) будет сложной функцией. Применив правило дифференцирования, получаем:

d 2 y d x 2 = d p d y d y d x = d p d y p ( y ) d 3 y d x 3 = d d p d y p ( y ) d x = d 2 p d y 2 d y d x p ( y ) + d p d y d p d y d y d x = = d 2 p d y 2 p 2 ( y ) + d p d y 2 p ( y )
Полученный результаты подставляем в исходное выражение. При этом мы получим дифференциальное уравнение, порядок которого на единицу меньше, чем у исходного.

Рассмотрим решение уравнения 4 y 3 y ‘ ‘ = y 4 — 1 . Путем замены d y d x = p ( y ) приведем исходное выражение к уравнению с разделяющимися переменными 4 y 3 p d p d y = y 4 — 1 .

Более подробно решения задач по теме рассмотрены в разделе «Дифференциальные уравнения, допускающие понижение порядка».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = 0 и y ( n ) + f n — 1 · y ( n — 1 ) + . . . + f 1 · y ‘ + f 0 · y = f ( x )

Решение уравнений данного вида предполагает выполнение следующих простых шагов:

• находим корни характеристического уравнения k n + f n — 1 · k n — 1 + . . . + f 1 · k + f 0 = 0 ;
• записываем общее решение ЛОДУ y 0 в стандартной форме, а общее решение ЛНДУ представляем суммой y = y 0 + y

— частное решение неоднородного дифференциального уравнения.

Нахождение корней характеристического уравнения подробно описано в разделе «Решение уравнений высших степеней». Для нахождения y

целесообразно использовать метод вариации произвольных постоянных.

Линейному неоднородному ДУ с постоянными коэффициентами y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = x cos x + sin x соответствует линейное однородное ДУ y ( 4 ) + y ( 3 ) — 5 y ‘ ‘ + y ‘ — 6 y = 0 .

Более детальный разбор теории и примеров по теме вы можете найти на странице « Линейные однородные и неоднородные дифференциальные уравнения высших порядков с постоянными коэффициентами».

Линейные однородные и неоднородные дифференциальные уравнения высших порядков y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 и y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = f ( x )

Найти решение ЛНДУ высших порядков можно благодаря сумме y = y 0 + y

, где y 0 — общее решение соответствующего ЛОДУ, а y

— частное решение неоднородного дифференциального уравнения.

y 0 представляет собой линейную комбинацию линейно независимых функций y 1 , y 2 , . . . , y n , каждая из которых является частным решением ЛОДУ, то есть, обращает равенство y ( n ) + f n — 1 ( x ) · y ( n — 1 ) + . . . + f 1 ( x ) · y ‘ + f 0 ( x ) · y = 0 в тождество. Частные решения y 1 , y 2 , . . . , y n обычно подбираются из известных систем линейно независимых функций. Подобрать их далеко не всегда просто и возможно, в этом и заключается основная проблема.

После того, как мы найдем общее решение ЛОДУ, найти частное решение соответствующего ЛНДУ можно благодаря методу вариации произвольных постоянных. Итак, y = y 0 + y

Получить более подробную информацию по теме можно в разделе «Дифференциальные уравнения высших порядков».

Системы дифференциальных уравнений вида d x d t = a 1 x + b 1 y + c 1 d y d t = a 2 x + b 2 y + c 2

Данная тема подробно разобрана на странице «Системы дифференциальных уравнений». Там же приведены примеры задач с подробных разбором.