Уравнение сферы через четыре точки

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

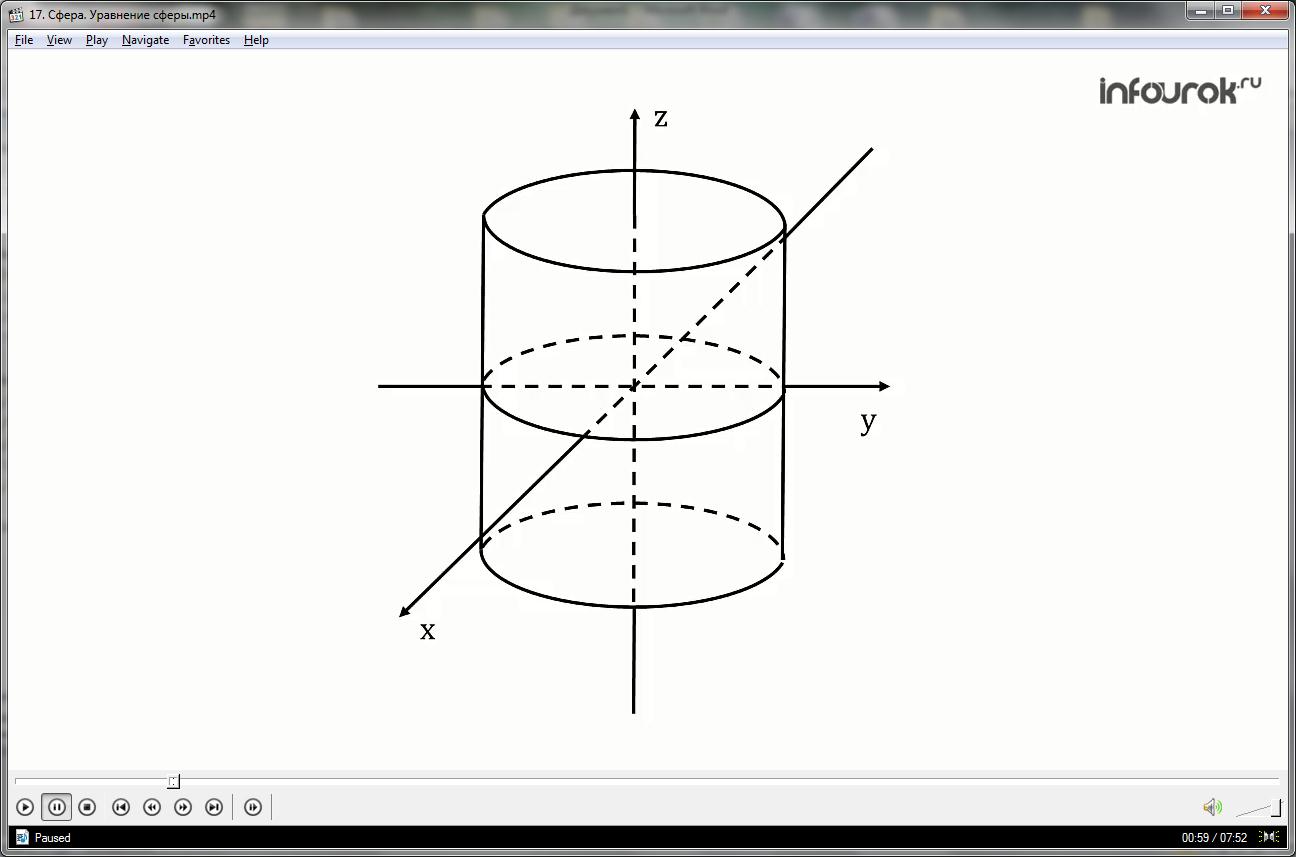
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

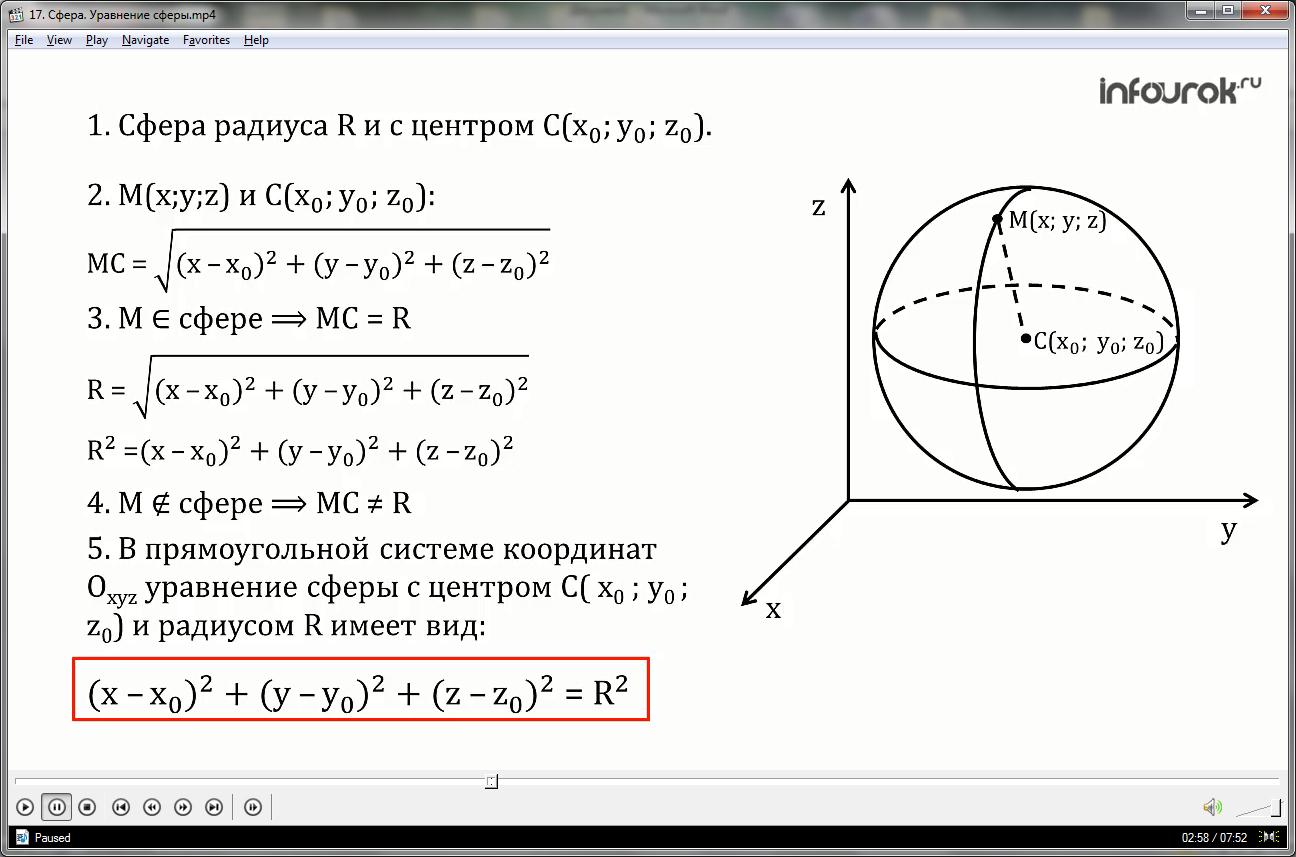
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

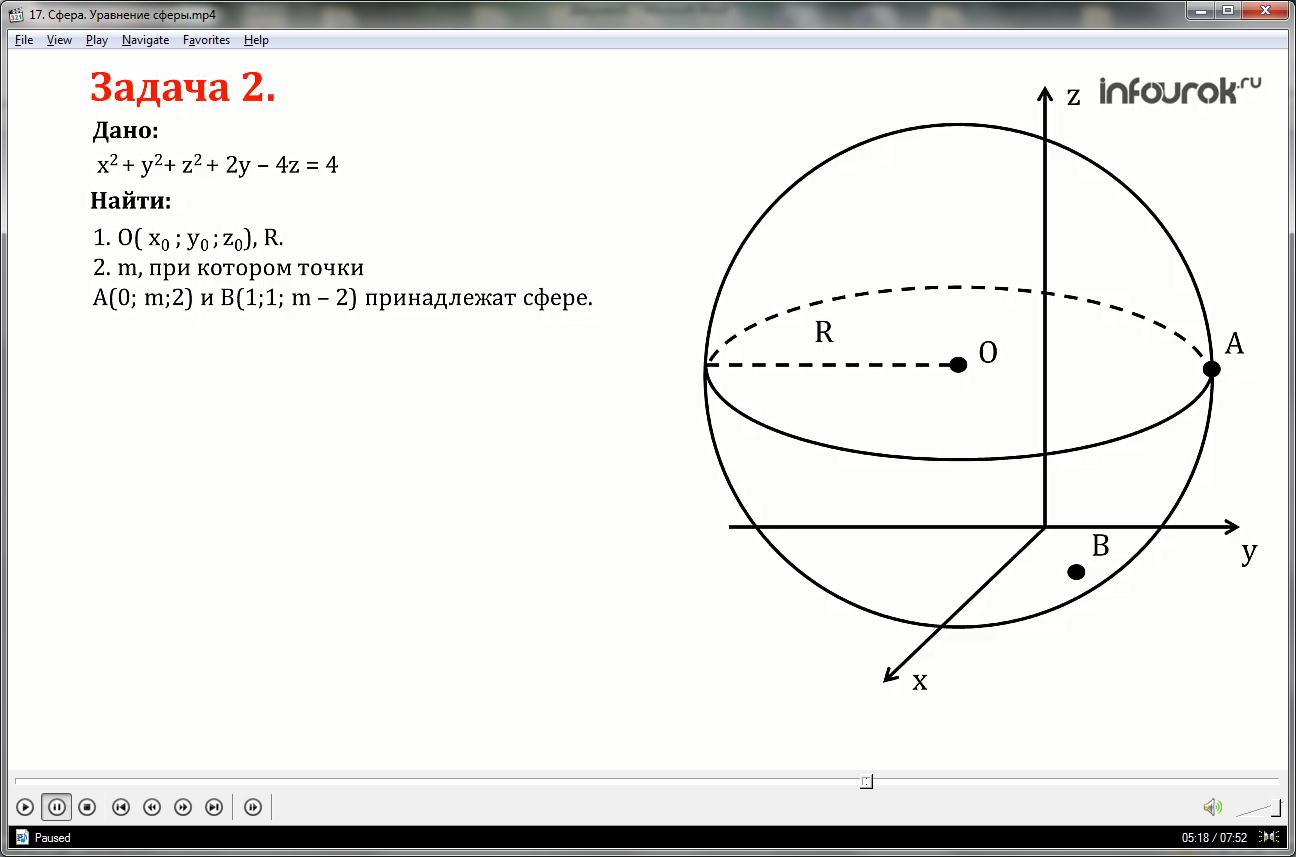
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

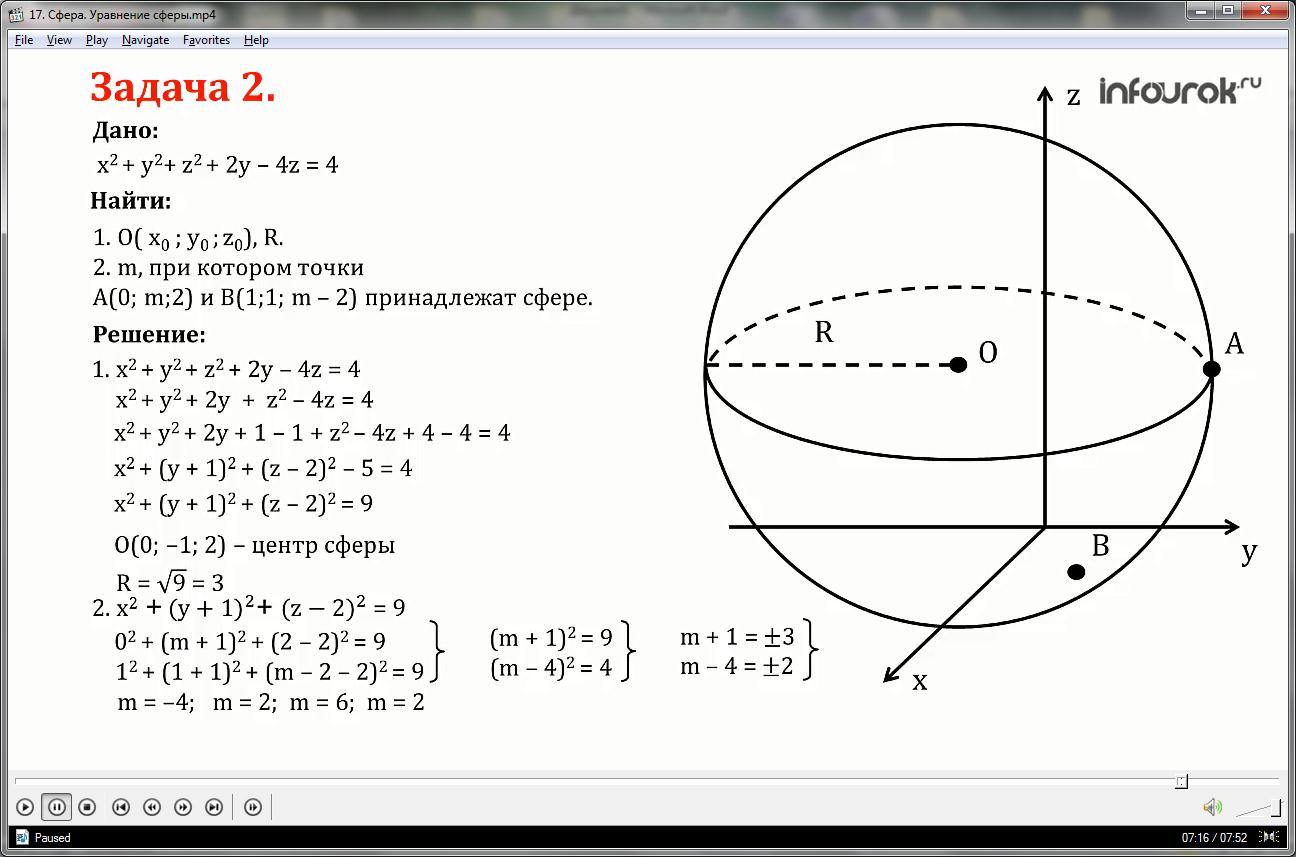
1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

51815

1003

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Уравнение сферы через четыре точки

Построим сферу, проходящую через четыре несовпадающие точки, расположенные в трехмерном пространстве. Идея алгоритма состоит в следующем: все точки сферы одинаково удалены от ее центра. Возьмем первую и вторую точки, задающие сферу и найдем то множество точек, которые равноудалены от них. Понятно, что такие точки будут находиться на плоскости, проходящей через центр отрезка, соединяющего первую и вторую точку, причем эта плоскость будет перпендикулярна этому отрезку.

Аналогичные рассуждения можно провести в отношении первой и третьей, а также первой и четвертой точек. Таким образом, будет образовано три несовпадающие плоскости, определенные на парах обозначенных выше точек. Как известно, три несовпадающие плоскости пересекаются в единственной точке. Понятно, что эта точка будет удалена на равные расстояния от всех четырех точек, задающих сферу. Она и будет являться центром искомой сферы. Для определения радиуса сферы необходимо измерить длину отрезка между центром сферы и любой из задающей ее точек.

Задача сводится к решению следующих подзадач:

— нахождение середин отрезков, соединяющих первую точку с остальными точками;
— построение плоскостей, проходящих через середины отрезков и перпендикулярных этим отрезкам;
— нахождение точки пересечения трех плоскостей;
— определение длины отрезка, соединяющего центр сферы и одну из определяющих ее точек;
— построение сферы по центру и радиусу.

Приступим к реализации алгоритма решения задачи.

Для решения поставленной задачи нам потребуется использовать алгоритм пересечения двух плоскостей. Такой алгоритм уже был разработан в проекте под названием «Пересечение плоскостей«. Для того чтобы не создавать его заново, воспользуемся примером из этого проекта, загрузим его в систему Симплекс и скопируем алгоритм пересечения плоскостей в буфер Clipboard. Для этого перейдем в окно алгоритма Прямая пересечения двух плоскостей, вызовем контекстное меню этого окна щелчком правой кнопки мыши и выберем в нем пункт Алгоритм... В появившемся окне следует перейти в Список алгоритмов проекта, выделить в нем алгоритм alg1 и, вызвав контекстное меню, выбрать пункт Копировать «alg1». В результате этого действия алгоритм и описание всех его параметров будут занесены в буфер Clipboard. Впоследствии мы вставим эту информацию в наш новый проект, реализующий задачу построения сферы по четырем точкам.

Теперь можно закрыть окно Список алгоритмов и вызвать команду создания нового проекта Ctrl+N.

Разместим курсор над открывшимся окном алгоритма Главный и, вызвав контекстное меню щелчком правой кнопки мыши, выберем пункт Вставить. В ответ на это действие система задаст вопрос о том, каким образом согласовать имена объектов алгоритма, хранящихся в буфере Clipboard, с именами объектов в алгоритме, в который производится вставка. Потенциально в алгоритмах могут быть объекты с одинаковыми именами, что может привести к конфликту состава отношений алгоритма. Но, поскольку, алгоритм Главный пуст, никаких конфликтов не возникнет и мы сможем произвести обыкновенную вставку, не выполняющую операцию замены имен вставляемого алгоритма на новые, неиспользуемые в алгоритме-приемнике.

Выполненная вставка не приводит к каким-либо видимым изменениям в проекте. Проверить то, что изменения все-же произошли, можно, вызвав из контекстного меню пункт Алгоритм, и убедиться в том, что в состав алгоритма включен алгоритм alg1 (Прямая пересечения двух плоскостей).

В настоящий момент имеет смысл выполнить команду сохранения проекта в файле на носителе информации, обратившись к пункту главного меню Файл/Сохранить как.

Для решения задачи потребуется еще один алгоритм, отвечающий за построение плоскости, проходящей через точку и перпендикулярной к заданному отрезку. Пользуясь командой проведения Свободной прямой, построим две произвольные линии o1 и o2, являющиеся проекциями некоторой прямой, расположенной в трехмерном пространстве. Изменим атрибут линии o2 на пунктирное начертание, для того чтобы визуально соотносить эту линию с объектами горизонтального поля проекций

2Разместим курсор где-нибудь над прямой o1 и выполним щелчок левой кнопкой мыши при нажатой клавише Ctrl, чтобы сгенерировать точку, принадлежащую прямой o1.

3Проведем через точку p1 вертикальную линию связи, предварительно выделив эту точку и нажав на клавиатуре кнопку с латинским символом v. Добавим к полученной и выделенной в данный момент линии o3 линию o2, удерживая при этом нажатой клавишу Shift, и нажмем на клавиатуре клавишу с латинским символом p, для того чтобы найти точку p2 пересечения двух прямых линий o2 и o3.

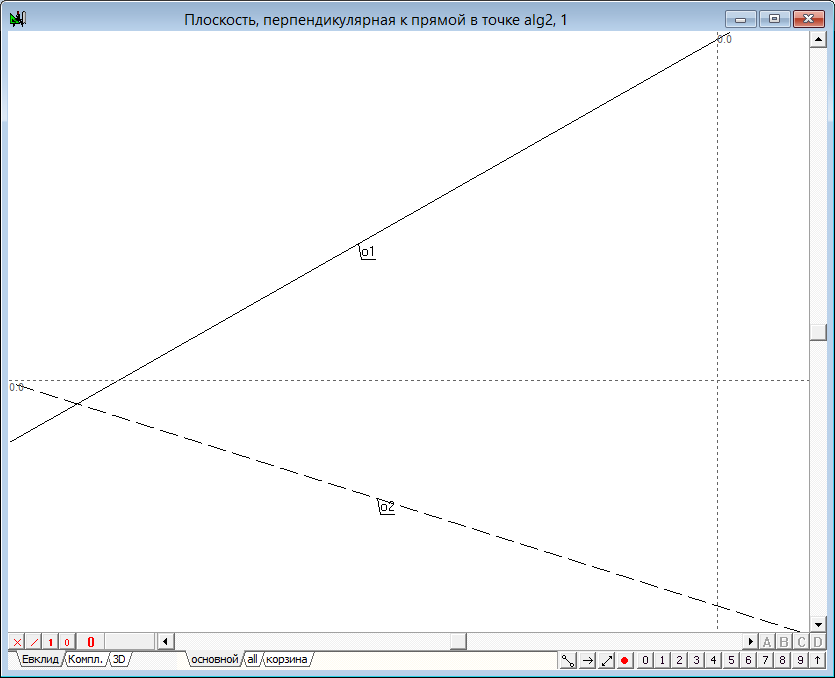
Прямые линии, задающие искомую плоскость, строятся следующим образом:

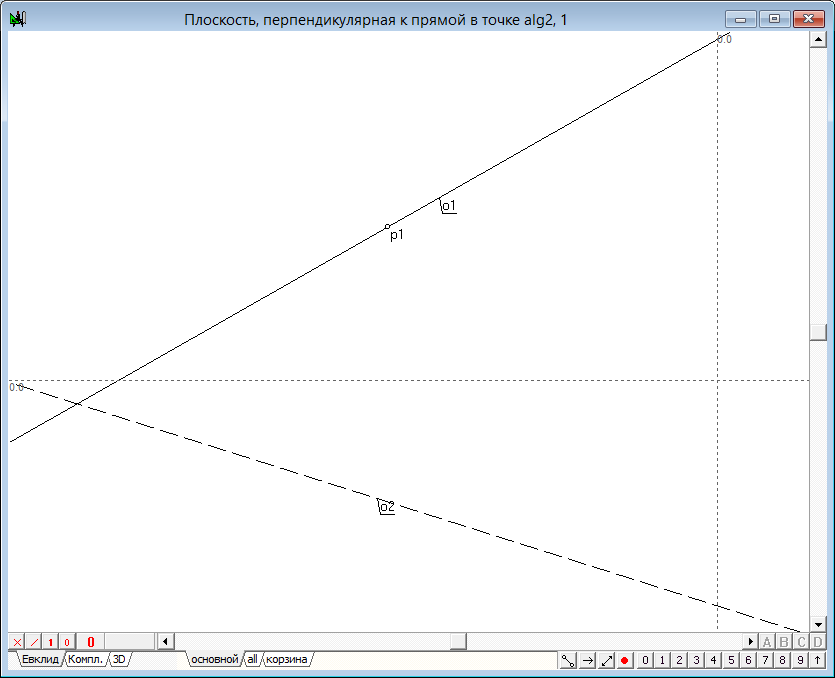
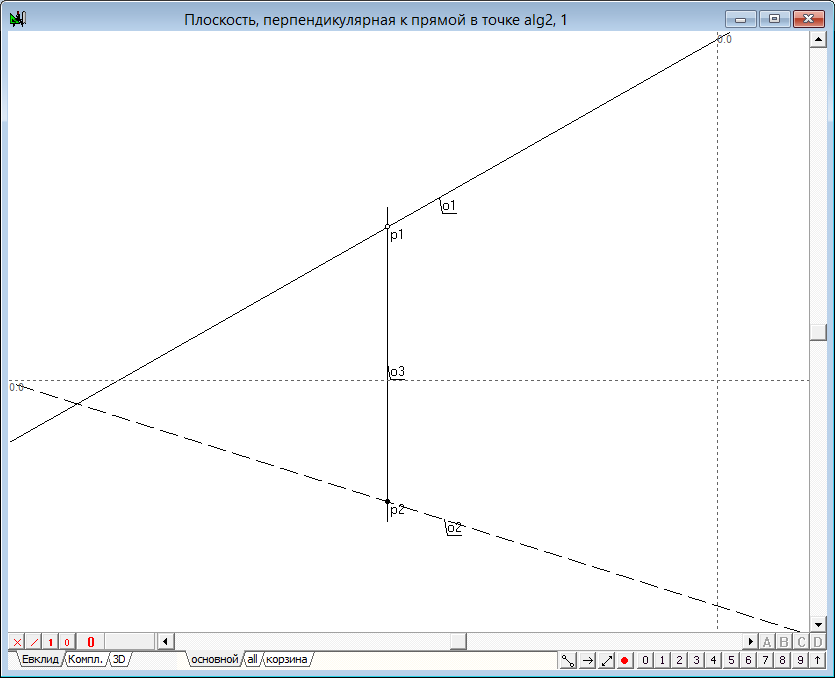
— фронтальная проекция прямой прямой плоскости, перпендикулярной к линии, заданной проекциями o1—o2 должна пройти через точку p1 горизонтально. Для ее построения выделяем точку p1, нажимаем на клавиатуре клавишу с латинским символом h, изменяем атрибут цвета на красный и атрибут начертания на укороченный (клавиша с цифрой 9).

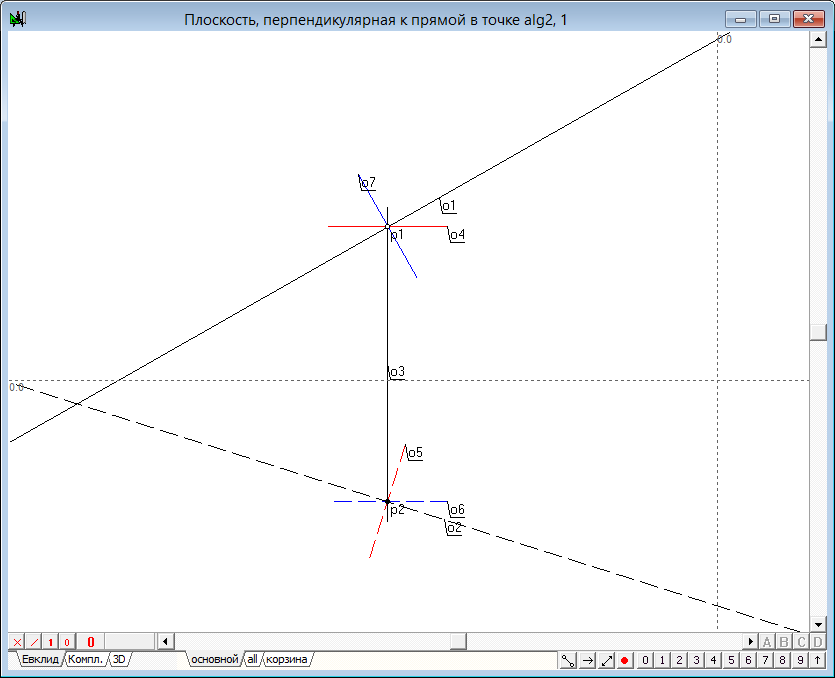
— горизонтальная проекция первой прямой плоскости o5 должна пройти перпендикулярно горизонтальной проекции исходной прямой через точку p2. Для ее построения выделим два объекта — точку p2 и прямую o2 и нажмем на клавиатуре клавишу с латинским символом o. Изменим атрибуты отображения этой прямой.

Проекции второй прямой плоскости строятся по аналогичному правилу лишь с той разницей, что теперь проекция прямой на горизонтальную плоскость должна проходить через точку p2 и быть строго горизонтальной, в то время как фронтальная проекция должна быть перпендикулярной фронтальной проекции исходной прямой и проходить через точку p1.

Реализация алгоритма выполнена. Теперь необходимо определить интерфейс взаимодействия с алгоритмом. Выделим последовательно объекты o4, o5, o7, o6 и, вызвав контекстное меню, назначим их выходными параметрами алгоритма. Вход алгоритма определим следующим образом: Выделим объекты p1, p2, o1, o2 и назначим их входными параметрами алгоритма. Укажем имя алгоритма (Плоскость, перпендикулярная к прямой в точке) и названия входных и выходных параметров.

p1 — 1-я проекция точки;
p2 — 2-я проекция точки;
o1 — 1-я проекция прямой;
o2 — 2-я проекция прямой.

o4 — 1-я проекция 1-ой прямой плоскости;
o5 — 2-я проекция 1-ой прямой плоскости;
o7 — 1-я проекция 2-ой прямой плоскости;
o6 — 2-я проекция 2-ой прямой плоскости.

Приступим к решению основной задачи.

Перейдем в окно алгоритма Главный и разместим в поле чертежа модели четырех точек, расположенных в трехмерном пространстве. Для этого, перемещая курсор по полю чертежа, будем нажимать на клавишу с латинским символом V (верхний регистр). Следует обратить внимание на то, что перед вводом каждой очередной команды необходимо снимать выделение, переводя курсос в поле, свободное от изображений объектов чертежа, и щелкая левой кнопкой мыши.

Уравнение сферы, проходящей через 4 точки

Напишите его уравнение сферы, которая проходит через точки $$ а (-5,4,1), б (3,4, -5), с (0,0,4), д (0,0,0) $$ Я попытался использовать четыре точки, чтобы нарисовать геометрическую форму, а затем вычислить центр этой формы на основе круга, проходящего по четырем точкам. Но мне это не удалось

Вот ответ книги $$ х ^ 2 + у ^ 2 + г ^ 2 + 54x-58y + 4z = 0 $$

$$\left | \begin x^2 + y^2 + z^2 & x & y & z & 1 \\ x_1^2 + y_1^2 + z_1^2 & x_1 & y_1 & z_1 & 1 \\ x^2_2 + y_2^2 + z_2^2 & x_2 & y_2 & z_2 & 1 \\ x_3^2 + y_3^2 + z_3^2 & x_3 & y_3 & z_3 & 1 \\ x_4^2 + y_4^2 + z_4^2 & x_4 & y_4 & z_4 & 1 \end \right | = 0 $$

т. е. $ -128 (x ^ 2 + y ^ 2 + z ^ 2-4x- \ frac <29> <2>y-4z) = 0 $

Используя уравнение для точек на сферах:

$ \ Qquad (х-а) ^ 2 + (у-б) ^ 2 + (г-с) ^ 2 = R ^ 2 $

Используя координаты четырех предоставленных точек, мы имеем четыре одновременных уравнения для решения для $ a, b, c, d $. \ BEGIN <случаи>(-5-a) ^ 2 + (4-b) ^ 2 + (1-c) ^ 2 = r ^ 2 \\ (3-a) ^ 2 + (4-b) ^ 2 + (-5-c) ^ 2 = r ^ 2 \\ (0-a) ^ 2 + (0-b) ^ 2 + (4-c) ^ 2 = r ^ 2 \\ (0-а) ^ 2 + (0-б) ^ 2 + (0-с) ^ 2 = R ^ 2 \ конец <случаи>(Выделение третьего и четвертого уравнений дает $ c $, а первые два дают $ a $, затем $ b $, тогда у вас есть $ r $, легко решаемая на бумаге)

и получить неотрицательное решение: \ BEGIN <случаи>a = 2 \\ b = \ frac <29> <4>\\ c = 2 \\ г = \ гидроразрыва <\ SQRT <969>> <4>\ конец <случаи>(просто решил, возможно, вы можете проверить ответы: D)

уравнение сферы задается формулой $$ (x-x_M) ^ 2 + (y-y_M) ^ 2 + (z-z_M) ^ 2 = R ^ 2 $$ вставляя данные координаты, вы получите $$ (- 5-x_M) ^ 2 + (4-y_M) ^ 2 + (1-z_M) ^ 2 = R ^ 2 $$ (I) $$ (3-x_M) ^ 2 + (4-y_M) ^ 2 + (- 5-z_M) ^ 2 = R ^ 2 $$ (II) $$ x_M ^ 2 + y_M ^ 2 + (4-z_M) ^ 2 = R ^ 2 $$ (III) $$ x_M ^ 2 + y_M ^ 2 + z_M ^ 2 = R ^ 2 $$ (IV) решить эту систему для $ x_M, y_M, z_M $ и $ R $ и теперь вычесть (I) — (II), например

Техника здесь проста.

Сначала возьмем общее уравнение сферы:

$$ (х-а) ^ 2 + (у-б) ^ 2 + (г-с) ^ 2 = R ^ 2 $$

Если это проходит через точки $ (x_1, y_1, z_1) $ и $ (x_2, y_2, z_2) $, то у вас есть два уравнения:

$$ (x_1-а) ^ 2 + (y_1-б) ^ 2 + (z_1-с) ^ 2 = R ^ 2 $$$$ (x_2-а) ^ 2 + (y_2-б) ^ 2 + ( z_2-с) ^ 2 = R ^ 2 $$

Теперь вычтем второй из первого $$ x_1 ^ 2-x_2 ^ 2 + 2a (x_2-x_1) + y_1 ^ 2-y_2 ^ 2 + 2b (y_2-y_1) + z_1 ^ 2-z_2 ^ 2 + 2c (z_2 -z_1) = 0 $$

Теперь у вас есть линейное уравнение в трех неизвестных, $ a, b, c $ — неудобные квадратные члены все отменяют. У вас достаточно данных для получения трех независимых уравнений, которые вы должны решить. Здесь вы можете сделать несколько лучше, выбрав точку $ (0,0,0) $ в качестве второй точки в каждом случае, которая дает $$ 2ax_1 + 2by_1 + 2cz_1 = x_1 ^ 2 + y_1 ^ 2 + z_1 ^ 2 $$ и дает вам более простую арифметику.

Уравнение сферы с центром в $ (x_0, y_0, z_0) $ и радиусом $ r $ равно $ (x-x_0) ^ 2 + (yy ^ 0) ^ 2 + (z-z_0) ^ 2 = R ^ 2 $. Для нас неизвестными являются $ x_0, y_0, z_0, r $.

Подключите следующие четыре точки:

$$ \ begin (- 5-x_0) ^ 2 + (4-y_0) ^ 2 + (1-z_0) ^ 2 = r ^ 2 \\ (3-x_0) ^ 2 + (4-y_0) ^ 2 + (- 5-z_0) ^ 2 = r ^ 2 \\ (-x_0) ^ 2 + (- y_0) ^ 2 + (4-z_0) ^ 2 = r ^ 2 \\ (-x_0) ^ 2 + (- y_0) ^ 2 + (- z_0) ^ 2 = r ^ 2 \ end $$

или (после небольшого преобразования):

$$ \ begin 42 + 10x_0-8y_0-2z_0 + x_0 ^ 2 + y_0 ^ 2 + z_0 ^ 2 = r ^ 2 \\ 50-6x_0-8y_0 + 10z_0 + x_0 ^ 2 + y_0 ^ 2 + z_0 ^ 2 = r ^ 2 \\ 16-8z_0 + x_0 ^ 2 + y_0 ^ 2 + z_0 ^ 2 = r ^ 2 \\ x_0 ^ 2 + y_0 ^ 2 + z_0 ^ 2 = r ^ 2 \ end $$

Теперь отнимите одно из уравнений от остальных (в этом случае последнее самое простое):

$$ \ begin 42 + 10x_0-8y_0-2z_0 = 0 \\ 50-6x_0-8y_0 + 10z_0 = 0 \\ 16-8z_0 = 0 \\ x_0 ^ 2 + y_0 ^ 2 + z_0 ^ 2 = r ^ 2 \ end $$

Решите систему первых трех (линейных) уравнений, чтобы получить: $ x_0 = 2, y_0 = \ frac <29><4>, z_0 = 2 $. Подключите это к четвертому, чтобы получить $ r = \ sqrt <2 ^ 2 + \ left (\ frac <29> <4>\ right) ^ 2 + 2 ^ 2> = \ frac <\ sqrt <969>> <4 >$.

Таким образом, окончательное уравнение:

$$ (x-2) ^ 2 + (y- \ frac <29><4>) ^ 2+ (z-2) ^ 2 = \ frac <969> <16>$$

или, после преобразования:

$$ x ^ 2 + y ^ 2 + z ^ 2-4x- \ frac <29> <2>y-4z = 0 $$

поскольку все постоянные члены будут отменять друг друга.