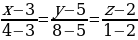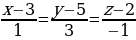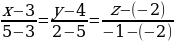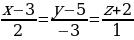Уравнение сферы плоскости и прямой лекция

Уравнение прямой, плоскости и сферы

306 гр. Математика. Дистанционное обучение. Тема 1-3.

Просмотр содержимого документа
«Уравнение прямой, плоскости и сферы»

Тема 1: Уравнение прямой в пространстве.

З адание: записать конспект и выполнить самостоятельную работу.

Пример 1. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Подставив в уравнение прямой соответствующие координаты, получим:

Упростим:

Ответ: 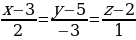Самостоятельная работа

Пример 1. Составить уравнение прямой, проходящей через две точки:

Пример 2. Составить уравнение прямой, проходящей через две точки:

Пример 3. Составить уравнение прямой, проходящей через две точки:

Тема 2: Уравнение плоскости в пространстве

Задание: записать конспект и выполнить самостоятельную работу

П 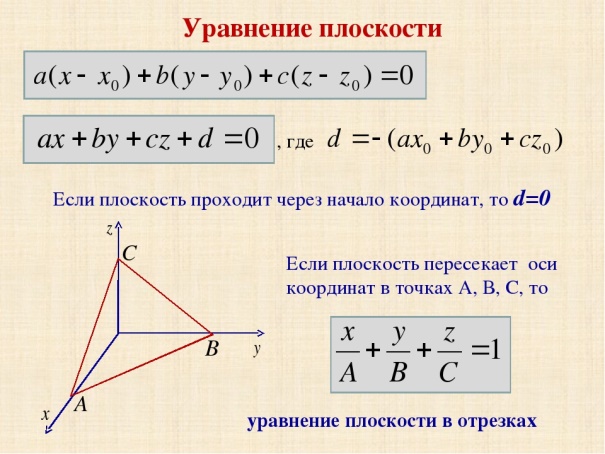ример 1: Принадлежит, ли точка В (-1; 2; 7) плоскости, заданной уравнением 2х+3у-z+3=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство.

Ответ: точка В (-1; 2; 7) принадлежит плоскости.

Пример 2: Принадлежит, ли точка Е(0; 4; -6) плоскости, заданной уравнением х-5у-4z+2=0

Решение: Подставим координаты точки в уравнение и проверим верно ли равенство. х-5у-4z+2=0

0-5·4-4·(-6)+2=0-20+24+2=6≠0 не верно

Ответ: точка Е(0; 4; -6) не принадлежит плоскости.

Пример 3: При каком D точка А(1; 5;-2) принадлежит плоскости -3х+2у-z+D=0

Решение: Подставим координаты точки в уравнение и найдем D.

Пример 1: Принадлежит, ли точка В (-2; 3; 8) плоскости, заданной уравнением

Пример 2: Принадлежит, ли точка Е(3; 4; -2) плоскости, заданной уравнением

Пример 3: При каком D точка А(2; 4;-1) принадлежит плоскости -2х+5у-z+D=0

Решить задания №1, №2

О пределение. Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии R от данной точки О.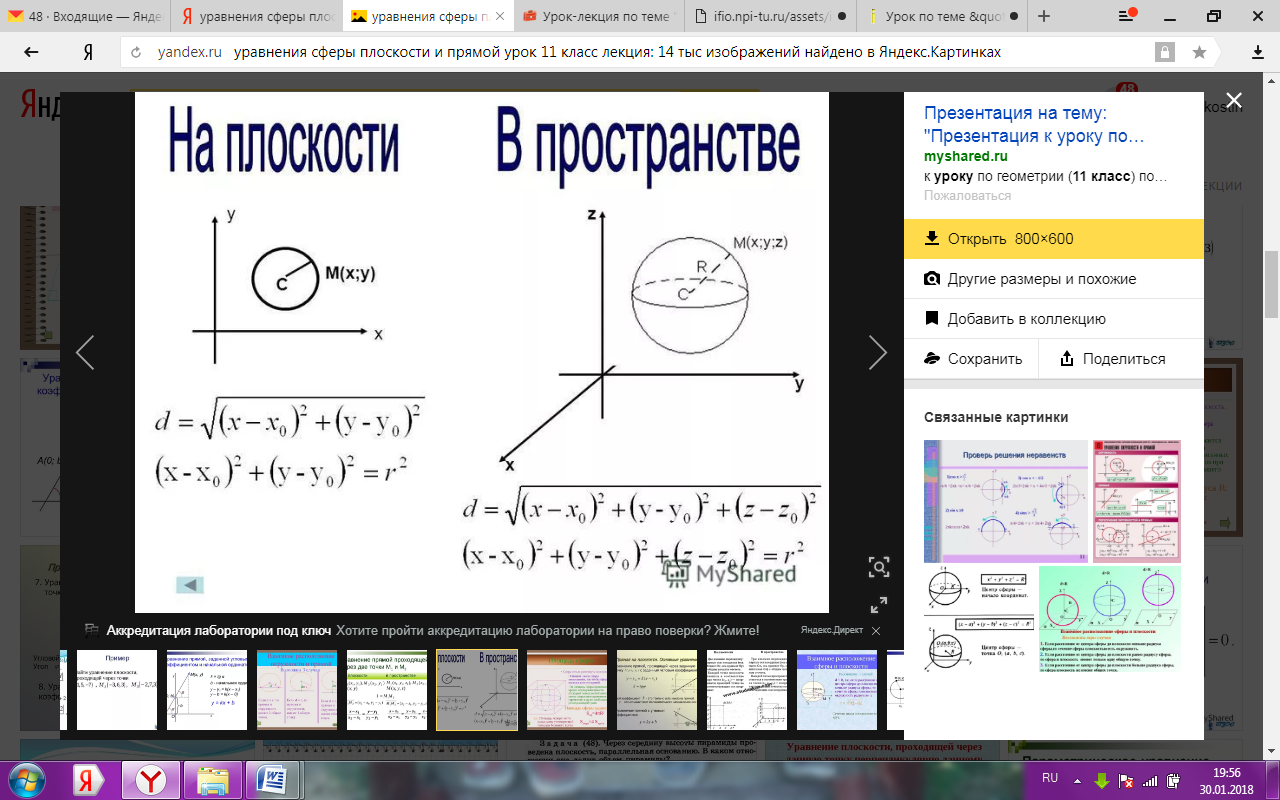

R – радиус сферы, т. О – центр сферы.

Написать уравнение сферы с центром в точке О(1; 2; -5) и радиусом R=3.

Подставим в уравнение сферы: (х-1) 2 +(у-2) 2 +(z-(-5)) 2 =3 2 .

Упростим: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Ответ: (х-1) 2 +(у-2) 2 +(z+5) 2 =9.

Пример 2. Дано уравнение сферы: (х-6) 2 +(у+3) 2 +(z-4) 2 =64. Найти координаты центра и радиус сферы.

1)найдем координаты центра: (х-6) 2 +(у-(-3)) 2 +(z-4) 2 =64

2)найдем радиус: R 2 =64, R=√64=8,

Ответ: О(6, -3, 4), R = 8.

Задание 1. Написать уравнение сферы с центром в точке О(5; -2; 3) и радиусом R= 6

Задание 2. Дано уравнение сферы (х-3) 2 +(у+7) 2 +(z-8) 2 =25. Найти координаты центра и радиус сферы.

Составление уравнений сферы, плоскости, прямой.
план-конспект занятия по геометрии (10, 11 класс)

Составление уравнений сферы, плоскости, прямой.

Скачать:

Предварительный просмотр:

Составление уравнений сферы, плоскости, прямой.

Цели: формировать умение обучающихся решать задачи на данную тему; развивать логическое мышление, пространственное воображение; умение сравнивать, проводить аналогию, воспитание трудолюбия, усердия в достижении цели, формировать общие компетенции ОК.2, ОК.3, ОК.4, ОК.5, ОК.6.

Справочный материал и примеры.

Теоретический материал для самостоятельного изучения:

Общее уравнение прямой имеет вид: Ax + By + C , где А, В, С – некоторые числа. При этом коэффициенты одновременно не равны нулю, так как уравнение теряет смысл.

Вектор нормали — это вектор, перпендикулярный искомой прямой. Вектор нормали чаще всего записывается так: ( n 1; n 2 ) Координаты точки ( х 0 ; у 0 ) .

Уравнение прямой по точке и направляющему вектору: Если известна некоторая точка, принадлежащая прямой, и направляющий вектор этой прямой, то уравнение данной прямой можно составить по формуле: n 1 (x-х 0 )+n 2 (y-у 0 )=0

Общее уравнение плоскости:

Общее уравнение плоскости имеет вид Ax +By+Cz+D=0 , где коэффициенты A, B, C, D одновременно не равны нулю.

Уравнение плоскости по точке и направляющему вектору: Если известна некоторая точка, принадлежащая плоскости, и вектор n, перпендикулярный этой плоскости (который называют вектором нормали к плоскости), то уравнение данной плоскости можно составить по формуле:

A(x-х 0 )+B(y-у 0 )+C(z-z 0 )=0

Уравнение поверхности сферы:

Сфера радиуса R с центром в начале координат представлена уравнением второй степени. x 2 +y 2 +z 2 =R 2 (R – радиус сферы)

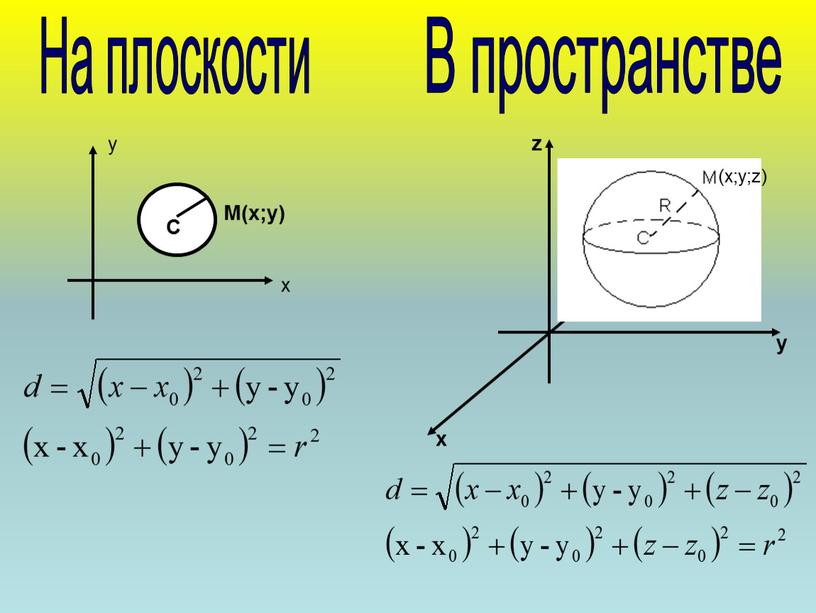
Сфера радиуса R центр которой не совпадает с началом координат представлена другим уравнением второй степени.

(x−a) 2 +(y−b) 2 +(z−c) 2 =R 2 (R — радиус сферы; a, b, c — смещение центра сферы относительно центра координат)

Задания для практической работы:

1. Составить уравнение сферы радиуса R = 5 с центром в начале координат.
2. Найти центр и радиус сферы (х+ 4) 2 + (y —3) 2 + z 2 =100.
3. Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.
4. Составить уравнение прямой по точке и направляющему вектору М (4, -2), n (3,2)
5. Составить уравнение плоскости по точке Р (4, -2; -1) и вектору нормали, n (-5;3,-2)
6. Доказать, что уравнение х 2 + у 2 + z 2 —2х+ 4у—6z+ 5 = 0, является уравнением сферы.
7. Найти уравнение прямой, проходящей через две точки: (-1, 2) и (2, 1).
8. Составить уравнение плоскости, проходящей через точку А и перпендикулярной вектору ВС, если А(-4; 2; -1), В(1; 2;-1), С(-2; 0; 1).

1. Какой вид имеет общее уравнение плоскости?
2. Какой вид имеет уравнение плоскости по точке и вектору нормали?
3. Какой вид имеет уравнение прямой по точке и направляющему вектору?
4. Какой вид имеет общее уравнение прямой?
5. Какой вид имеет уравнение сферы?

Уравнение сферы, плоскости, прямой

Понятие сферы и её элементов Уравнение сферы в заданной системе координат

Понятие сферы и её элементов
Уравнение сферы в заданной системе координат

Тело вращения — сфера

Тело вращения — сфера

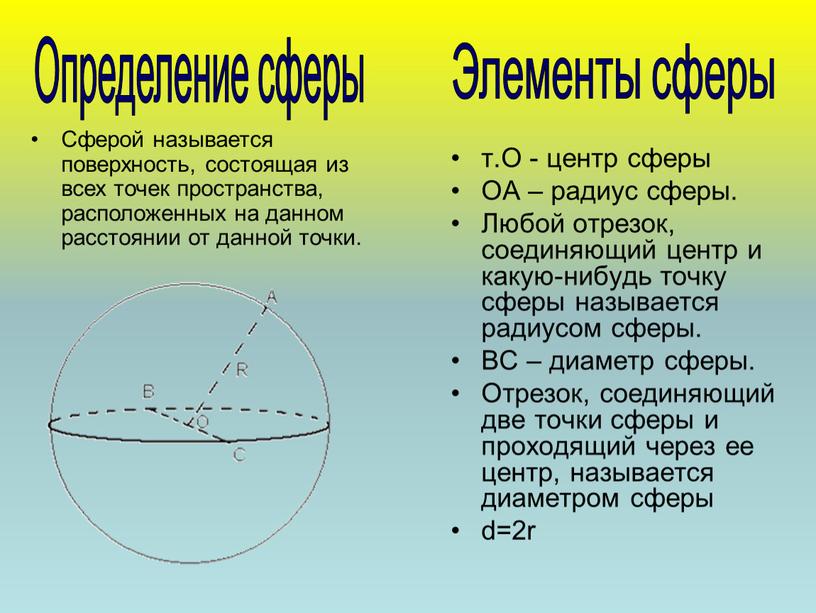
Определение сферы Элементы сферы

Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

т.О — центр сферы
ОА – радиус сферы.
Любой отрезок, соединяющий центр и какую-нибудь точку сферы называется радиусом сферы.
ВС – диаметр сферы.
Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы
d=2r

На плоскости В пространстве Уравнение с двумя переменными х и у называется уравнением линии

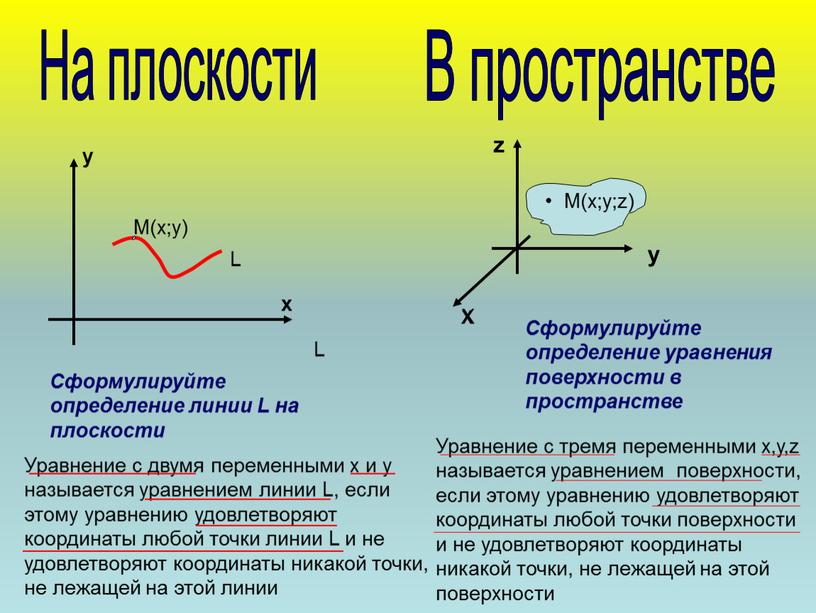
Уравнение с двумя переменными х и у называется уравнением линии L, если этому уравнению удовлетворяют координаты любой точки линии L и не удовлетворяют координаты никакой точки, не лежащей на этой линии

Уравнение с тремя переменными х,у,z называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки поверхности и не удовлетворяют координаты никакой точки, не лежащей на этой поверхности

На плоскости В пространстве М(х;у) х у х у z (х;у;z)

Уравнение плоскости и прямой

Уравнение плоскости и прямой

Общее уравнение плоскости Ax+By+Cz+D=0 где

Общее уравнение плоскости

где А, В, С, D – числовые коэффициенты

Особые случаи уравнения: D = 0 

Особые случаи уравнения:

D = 0  Ax+By+Cz = 0
плоскость проходит через начало координат.
А = 0  Ву + Cz +D = 0
плоскость параллельна оси Ох.
В = 0  Ах + Cz +D = 0
плоскость параллельна оси Оу.
C = 0  Ax+By+D = 0
плоскость параллельна оси Oz.

Особые случаи уравнения: А = В = 0 

Особые случаи уравнения:

А = В = 0  Сz + D = 0
плоскость параллельна плоскости Оху.
А = С = 0  Ву + D = 0
плоскость параллельна плоскости Охz.
В = C= 0  Ах+D = 0
плоскость параллельна плоскости Оуz.

Особые случаи уравнения: A = D = 0 

Особые случаи уравнения:

A = D = 0  By+Cz = 0
плоскость проходит через ось Ox.
B = D = 0  Ax + Cz = 0
плоскость параллельна оси Оy.
C = D = 0  Ах + By = 0
плоскость параллельна оси Оz.

Уравнения координатных плоскостей x = 0, плоскость

Уравнения координатных плоскостей

x = 0, плоскость Оyz
y = 0, плоскость Оxz
z = 0, плоскость Оxy

Две плоскости в пространстве: параллельны, если существует такое число k, что

совпадают, если существует такое число k, что

Две плоскости в пространстве:

параллельны, если существует такое число k, что

В остальных случаях плоскости пересекаются.

Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

Итак, пусть  произвольная плоскость в пространстве. Всякий перпендикулярный ей ненулевой вектор называется вектором нормали к этой плоскости.

Если известна какая-нибудь точка плоскости

Если известна какая-нибудь точка плоскости M0 и какой-нибудь вектор нормали к ней, то через заданную точку можно провести единственную плоскость, перпендикулярную данному вектору. Общее уравнение плоскости будет иметь вид:

Алгоритм составления уравнения плоскости, проходящей через точку перпендикулярно данному вектору

Чтобы получить уравнение плоскости , имеющее приведённый вид, возьмём на плоскости произвольную точку

Чтобы получить уравнение плоскости, имеющее приведённый вид, возьмём на плоскости произвольную точку M(x;y;z). Эта точка принадлежит плоскости только в том случае, когда вектор перпендикулярен вектору (рис), а для этого, необходимо и достаточно, чтобы скалярное произведение этих векторов было равно нулю, т.е.

Вектор задан по условию. Координаты вектора найдём по формуле :

Теперь, используя формулу скалярного произведения векторов , выразим скалярное произведение в координатной форме:

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору

Пример 1. Составить уравнение плоскости, проходящей через точку и перпендикулярной вектору .

Используем формулу
A(x-x0)+B(y-y0)+C(z-z0)=0

Решение:

Ответ: 5x + y — 4z — 3=0

Уравнение прямой в пространстве

Уравнение прямой в пространстве

Поскольку прямую в пространстве можно рассматривать как линию пересечения двух плоскостей, то одним из способов аналитического задания прямой в пространстве является задание с помощью системы из двух уравнений задающих пару пересекающихся плоскостей.

Уравнение прямой в пространстве

Уравнение прямой в пространстве

Прямую, проходящую через точку A0(x0,y0,z0) с направляющим вектором (a,b,c) можно задавать параметрическими уравнениями

В случае, если прямая в пространстве задается двумя точками A1(x1,y1,z1), A2(x2,y2,z2), то, выбирая в качестве направляющего векто­ра вектор (x2-x1,y2-y1,z2-z1) и в качестве точки А0 точку А1, получим следующие уравнения