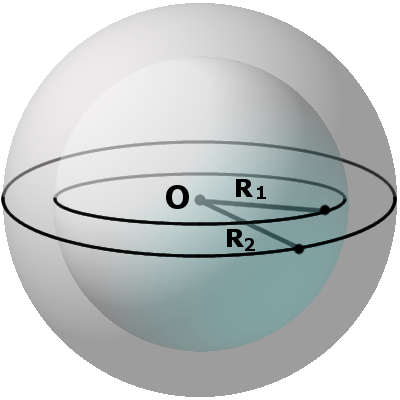
ПОСТРОЕНИЕ СФЕРЫ ПО ТОЧКАМ
English version
 | Гирш Антон Георгиевич | (Universität Kassel) |
Аннотация
Приводятся конструкции построения сферы по двум парам комплексно сопряжённых точек по аналогии с задачей построения сферы по четырём действительным точкам. Как необходимая поддержка построения сферы приводятся унифицированные конструктивные блоки (Бл.) по построению окружностей по комплексным точкам.
Ключевые слова: мнимые сопряжённые точки; носитель мнимых точек; касательные прямые; изотропные прямые; скрещивающиеся прямые; действительная окружность; мнимая окружность; круг Фалеса; линия центров; радикальная ось; параллельные плоскости; действительная сфера; мнимая сфера.
Введение
В статье предлагается построение сферы по четырём точкам. Точки могут все быть действительными, все быть мнимыми, пара быть действительными и пара мнимыми сопряжёнными. В статье предлагаются конструкции построения сферы, опирающиеся на конструктивные примитивы – блоки решений (Бл.) по построению точек пересечения прямой с окружностью и построению окружности по её точкам [1, 3, 4].
Условия задач
1. Построение сферы
Задача 1.1. Построить сферу Θ по четырём действительным точкам A, B, C, D в пространстве R.
Задача 1.2. Построить сферу Θ по двум парам мнимых сопряжённых точек A1, A2 и B1, B2 в пространстве C.
Задача 1.3. Построить сферу Θ по паре действительных точек A, B и паре мнимых сопряжённых точек C1, C2 в пространстве C.
2. Вычисление параметров сферы
Задача 2.1. Определить координаты центра и величину радиуса сферы Θ(C, R), заданной двумя парами мнимых точек с комплексными координатами A12(± 2i; 0; 0) и B12(3 ± i; ± 3.5 i; 2).
Задача 2.2. Определить координаты центра и величину радиуса сферы Θ(C, R), заданной двумя парами мнимых точек с комплексными координатами A12(± 4i; 0; 0) и B12(3 ± i; 2 ± 3.5 i; √7).
Задача 2.3. Определить координаты центра и величину радиуса сферы Θ(C, R), заданной двумя парами мнимых точек с комплексными координатами и A12(± 4i; 0; 0) и B1(2 + 2i; 4 — 3.5 i; 4), B2 (2 — 2i; 4 + 3.5 i; 4).
3. Содержание конструктивных блоков решений
Задача Бл.1. Определение главных точек M1, M2 в инволюционном ряду точек на прямой g.
Задача Бл.2. Построить точки пересечения прямой линии g с окружностью (C, R).
Задача Бл.3. Построить окружность по данному центру C и паре комплексно сопряжённых точек M1, M2.
Задача Бл.4. Построить окружность (C, R) по двум парам комплексно сопряжённых точек M1, M2 и N1, N2.
Задача Бл.5. Построить окружность (C, R) по паре действительных точек D1, D2 и паре комплексно сопряжённых точек M1, M2.
Построение сферы
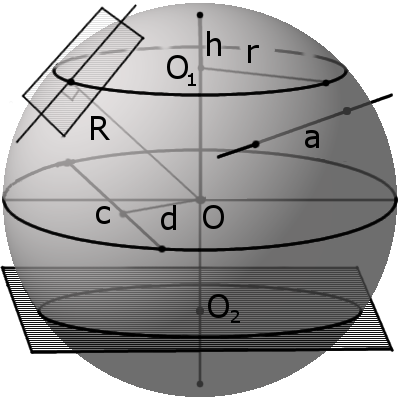
Конструктивные посылки: Четыре точки пространства определяют две прямые, которые в общем случае не параллельны, не пересекаются, а скрещиваются. Через две скрещивающиеся прямые всегда можно провести параллельные плоскости. Две параллельные плоскости всегда можно привести в положение уровня (плоскость уровня параллельна плоскости проекций), тогда на смежной проекции они будут изображаться двумя параллельными прямыми уровня. Исходя из этих посылок исходные точки принимаются лежащими попарно на прямых в плоскостях уровня, например, g1(A, B) – в плоскости Г1, g2(C, D) – в плоскости Г2.
На поле проекций П1 строят срединные перпендикуляры отрезков A1A2 и B1, B2, которые пересекаются в точке O’ – проекции центра искомой сферы Θ. С точкой O’ совпадает и проекция вертикальной ось вращения v сферы. Центр O’ лежит вне окружности (A1A2) – окружность, заданную центром и парой мнимых точек, строят по Бл.3, рис.2b – окружность (O’, R1) действительная. Далее, центр O’ лежит внутри окружности (B1B2) – окружность, заданную центром и парой мнимых точек, строят по Бл.3, рис.2c – окружность (O’, R2) мнимая. Обе окружности (O’, R1) и (O’, R2) рассекаются меридиональной плоскостью, первая по точкам D1 и D2, вторая по точкам M1 и M2, лежащих на проекции меридиана m. По линиям проекционной связи точки переносят на поле проекций П2 – точки D1 и D2 на линию Г1 – точки M1 и M2 на линию Г2. Построение проекции O» центра сферы выполняется по Бл.5а для разнородных пар точек. На фрагменте рис.1 А приведено построение центра и радиуса окружности, заданной двумя разнородными парами точек D1, D2 и M1, M2. Это пример того, как в унифицированном конструктивном блоке учитываются актуальные параметры задачи. Искомая окружность действительная, радиус равен длине отрезка от точки O до одной из действительных точек D1 или D2. Построенная окружность (O», r) является фронтальным очерком искомой сферы Θ(O, r). Вычисление параметров сферы Общее уравнение сферы имеет вид:
(x — x0)2 + (y — y0)2 + (z — z0)2 = r2.
В уравнение сферы последовательно подставляют координаты данных четырёх точек. В результате получится система четырёх уравнений с четырьмя неизвестными x0, y0, z0, r. Решение системы уравнение позволяет получить значения координат центра C(x0, y0, z0) и величину радиуса r искомой сферы Θ(C, r).
Решение системы уравнений по условиям задачи 2.1 даёт параметры сферы Θ(C, r): C(0; 2.8; — 0.7), r = 2. Условия задачи определяют действительную сферу.
Решение системы уравнений по условиям задачи 2.2 даёт параметры сферы Θ(C, r): C(0; 3; √7), r = 0. Условия задачи определяют сферу, выродившуюся в точку.
Решение системы уравнений по условиям задачи 2.3 даёт параметры сферы Θ(C, r): C(0; 2.666; 2.2), r = 2i, где i2 = -1. Условия задачи определяют мнимую сферу.
Конструктивные блоки решений задач
Две разделяющиеся пары действительных точек A1, A2 и B1, B2 на действительной прямой g образуют инволюционный ряд. Такой инволюционный ряд называют эллиптическим, он имеет пару мнимых двойных точек M1, M2. Полуокружности (A1A2) и (B1B2) пересекаются в точке L – точке Лагерра, с основанием в точке P – центре инволюционного ряда точек. Мнимые точки M1, M2 лежат на носителе на g. Центр C окружности, проходящей через мнимые точки M1, M2, будет лежать на прямой LP и её радиус будет меньше отрезка LP, рис.2а.
Прямая g не накладывается на действительную окружность (C, R) точки пересечения M1, M2 будут мнимыми, рис.2b. Строят круг Фалеса – окружность (CP), и отмечают точки пересечения R. Окружность (P, R) пересекает прямую g в точках M1, M2, рис.2b. Положение прямой g относительно мнимой окружности (C, R) безразлично. Через точку C параллельно прямой g проводят прямую p и отмечают точки R пересечения с окружностью (C). Окружность (P, R) пересекает прямую g в искомых точках M1, M2, рис.2с.
Данный центр C лежит вне окружности (M1M2), искомая окружность будет действительной. Строят круг Фалеса (CP) и отмечают точки R пересечения с окружностью (M1M2). Окружность (C, R) искомая. Данный центр C лежит внутри окружности (M1M2), искомая окружность будет мнимой. Через точку C параллельно прямой g проводят прямую p и отмечают точки R пересечения с окружностью(M1M2) . Окружность (C, R) искомая.
Прямые g1 и g2 параллельны, окружности (M1M2) и (N1N2) не пересекаются, искомая окружность будет действительной. Каждой окружности (M1M2) и (N1N2) придают некоторое касательное приращение δ, чтобы окружности пересеклись. Через точки пересечения вспомогательных окружностей проходит радикальная ось p.o. окружностей. Радикальная ось пересекает линию центров v данных окружностей в центре C искомой окружности. Радиус CR искомой окружности равен длине касательной из точки C к одной из окружностей (M1M2) или (N1N2), рис.3а. Прямые g1 и g2 параллельны, окружности (M1M2) и (N1N2) пересекаются, искомая окружность будет мнимой. На общей хорде окружностей как на диаметре строят окружность (C, R), являющейся носителем мнимой окружности. Мнимая окружность проходит через данные точки своими гиперболическими ветвями, на рис.3b ветви мнимой окружности не показаны.
Прямые g1 и g2 параллельны, точки D1 и D2 лежат вне окружности (M1M2), искомая окружность будет действительной. Строят радикальную ось разнородных окружностей. Для этого окружности (M1M2) придают некоторое касательное приращение δ, а окружности (D1D2) придают приращение равнобедренным треугольником с основанием D1D2 и сторонами δ. Через точки пересечения вспомогательных окружностей проходит радикальная ось p.o. окружностей. Радиус CR искомой окружности равен длине касательной из точки C к окружностей (M1M2). Окружность (C, R) проходит через действительные точки D1 и D2 и через точки M1 и M2 одной своей гиперболической ветвью, рис.4а – гиперболическая ветвь не показана. Прямые g1 и g2 параллельны, точки D1 и D2 лежат внутри окружности (M1M2). Задача имеет два решения, искомые окружности будет мнимыми. Носители мнимых окружностей проходят через точки D1, D2, через точки M1, M2 мнимые окружности проходят своими гиперболическими ветвями, рис.4 b.
Конструкция по рис.4 b имеет и чисто планиметрический интерес как решение задачи:
Даны окружность (M1M2) и внутренняя точка D. Построить окружность, проходящую через точку D, имеющую своим диаметром хорду окружности (M1M2), параллельную диаметру M1M2.
Автор имеет для этой задачи как точное решение [4, с.67], так и приближённое. Кроме чисто абстрактного упражнения, построение может служить конструктивным блоком для пространственных задач, например, построении сферы в этой статье. Изначально задача появилась как конструкция окружности псевдоэллиптического пучка с базисными точками M1, M2 по одной наперёд заданной точке D.
Заключение
Мы исходим из того, что построение сфер по четырём действительным точкам пространства, задача 1.1, известно [2]. Нами приведено построение сферы по двум парам мнимых сопряжённых точек. Построения сферы по двум парам разнородных точек, задача 1.3, укладывается в схему приведённой конструкции решения задачи 1.2. Кроме того, в работе приведены решения пяти вспомогательных задач на построение окружности по различным условиям образующих точек, встречающиеся в конструкциях сферы. Эти задачи обозначены как конструктивные блоки.
Задачи и упражнения по графическим построениям с включением мнимых элементов имеют целью укрепить уверенность исследователей в доступности восприятия мнимых образов как геометрических объектов и в возможности конструктивных построений с участием мнимых объектов – точек, прямых, окружностей, наравне с действительными объектами.
Список литературы
- Аргунов Б.И., Балк М.Б. Геометрические построения на плоскости. – М.: Просвещение, 1957. – 267 с.
- Курс начертательной геометрии. Четверухин Н.Ф. и др. – М.: ВШ, 1963. – 420 с.
- Гирш А.Г. Наглядная мнимая геометрия. – М.: ООО «ИПЦ «Маска»», 2008. – 213 с.
- Гирш А.Г. Комплексная геометрия – евклидова и псевдоевклидова: ООО «ИПЦ «Маска»», 2013. – 216 с.
- Гирш А.Г. Построение сферы по четырём мнимым элементам.// Электронный журнал по прикладной геометрии http:// www.mai.ru/
apg /Volume 10 №21 htm, 2008, cтр.48-56.
Рисунки к докладу
Построение сферы Θ(O, r) по двум парам мнимых точек A1, A2 и B1, B2
а) Бл.1 – определение мнимых точек M1, M2 в инволюционном ряду на g; b,
b) Бл.2 – построение мнимых точек M1, M2 пересечения прямой с окружностью; b,
с) Бл.3 – построение окружности по паре мнимых точек M1, M2 и центру C
Бл.4 – определение окружности (C, R) по двум парам мнимых точек M1, M2 и N1, N2
Бл.5 – определение окружности (C, R) по паре мнимых точек M1, M2 и паре действительных точек D1, D2
Вопросы и комментарии к выступлению:
 Головнин Алексей Алексеевич (22 февраля 2015 г. 2:51) | Здравствуйте уважаемый Антон Георгиевич! Любая комбинация из трех точек задает плоскость, которая пересекает искомую сферу по окружности. Остается провести перпендикуляр из центра окружности, проведенной через эти три точки. Повторим эту процедуру с другой комбинацией из трех точек и в точке пересечения перпендикуляров получим центр сферы. Но решение приведенной задачи по конструктивным посылкам, приведенным Вами, на мой взгляд, являет пример, когда знание начертательной геометрии (метод замены плоскостей проекций) приводит к более изящному решению, чем решение «в лоб» (встречал в литературе, что еще это называется путем грубой силы). Чаще начертательная геометрия применяется в учебных задачах, условие которых дано на эпюре Монжа, что само по себе сразу подразумевает, что задача должна решаться методами начертательной геометрии. 1. Может ли приведенная Вами задача служить примером, когда задача может быть решена аналитическими методами, но знание метода замены плоскостей проекций дает подсказку, какие математические выкладки использовать более рационально? 2. Находят ли мнимые окружности, построенные по комплексным точкам, применение в технике и если находят, то где, или Ваше исследование является развитием математической науки? С уважением Головнин А.А. | |||||||||||||
 Гирш Антон Георгиевич (22 февраля 2015 г. 15:52) | ||||||||||||||
| Принцев Николай Владимирович (27 февраля 2015 г. 19:54) | ||||||||||||||
 Гирш Антон Георгиевич (27 февраля 2015 г. 21:36) | ||||||||||||||
 Хейфец Александр Львович (22 марта 2015 г. 18:51) |
| V = | 4 | π R 3 = | 1 | π D 3 |
| 3 | 6 |
S = 4 π R 2 = π D 2
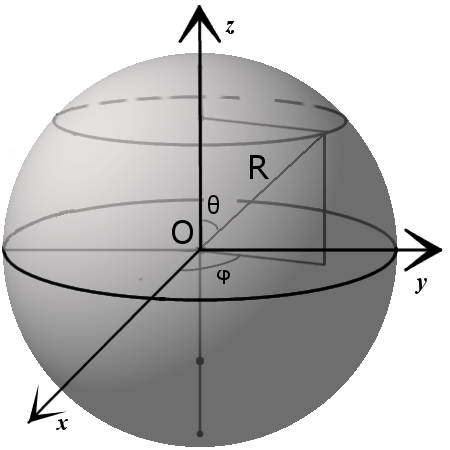
Уравнение сферы
x 2 + y 2 + z 2 = R 2
( x — x 0) 2 + ( y — y 0) 2 + ( z — z 0) 2 = R 2
Основные свойства сферы и шара
Секущая, хорда, секущая плоскость сферы и их свойства
d m между секущей плоскостью и центром сферы всегда меньше радиуса R:
m r такого круга можно найти по формуле:
где R — радиус сферы (шара), m — расстояние от центра шара до секущей плоскости.
Касательная, касательная плоскость к сфере и их свойства
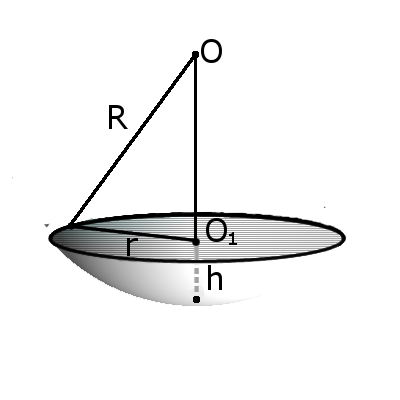
Формула. Объём сегмента сферы с высотой h через радиус сферы R:
| V = | h 2 π | (3R — h ) |
| 3 |
S = π R(2 h + √ 2 h R — h 2 )
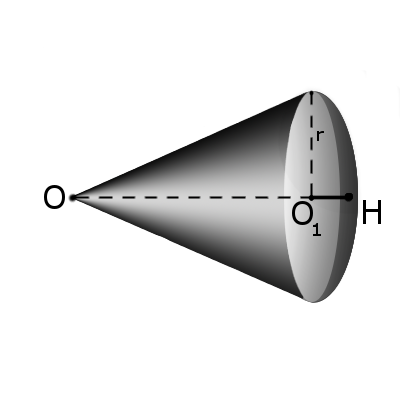
Формула. Объём сектора V с высотой O1H (h) через радиус шара OH (R):
| V = | 2 π R 2 h |
| 3 |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Уравнение сферы по 4 точкам
Построим сферу, проходящую через четыре несовпадающие точки, расположенные в трехмерном пространстве. Идея алгоритма состоит в следующем: все точки сферы одинаково удалены от ее центра. Возьмем первую и вторую точки, задающие сферу и найдем то множество точек, которые равноудалены от них. Понятно, что такие точки будут находиться на плоскости, проходящей через центр отрезка, соединяющего первую и вторую точку, причем эта плоскость будет перпендикулярна этому отрезку.
Аналогичные рассуждения можно провести в отношении первой и третьей, а также первой и четвертой точек. Таким образом, будет образовано три несовпадающие плоскости, определенные на парах обозначенных выше точек. Как известно, три несовпадающие плоскости пересекаются в единственной точке. Понятно, что эта точка будет удалена на равные расстояния от всех четырех точек, задающих сферу. Она и будет являться центром искомой сферы. Для определения радиуса сферы необходимо измерить длину отрезка между центром сферы и любой из задающей ее точек.
Задача сводится к решению следующих подзадач:
— нахождение середин отрезков, соединяющих первую точку с остальными точками;
— построение плоскостей, проходящих через середины отрезков и перпендикулярных этим отрезкам;
— нахождение точки пересечения трех плоскостей;
— определение длины отрезка, соединяющего центр сферы и одну из определяющих ее точек;
— построение сферы по центру и радиусу.
Приступим к реализации алгоритма решения задачи.
Для решения поставленной задачи нам потребуется использовать алгоритм пересечения двух плоскостей. Такой алгоритм уже был разработан в проекте под названием «Пересечение плоскостей«. Для того чтобы не создавать его заново, воспользуемся примером из этого проекта, загрузим его в систему Симплекс и скопируем алгоритм пересечения плоскостей в буфер Clipboard. Для этого перейдем в окно алгоритма Прямая пересечения двух плоскостей, вызовем контекстное меню этого окна щелчком правой кнопки мыши и выберем в нем пункт Алгоритм... В появившемся окне следует перейти в Список алгоритмов проекта, выделить в нем алгоритм alg1 и, вызвав контекстное меню, выбрать пункт Копировать «alg1». В результате этого действия алгоритм и описание всех его параметров будут занесены в буфер Clipboard. Впоследствии мы вставим эту информацию в наш новый проект, реализующий задачу построения сферы по четырем точкам.
Теперь можно закрыть окно Список алгоритмов и вызвать команду создания нового проекта Ctrl+N.
Выполненная вставка не приводит к каким-либо видимым изменениям в проекте. Проверить то, что изменения все-же произошли, можно, вызвав из контекстного меню пункт Алгоритм, и убедиться в том, что в состав алгоритма включен алгоритм alg1 (Прямая пересечения двух плоскостей).
В настоящий момент имеет смысл выполнить команду сохранения проекта в файле на носителе информации, обратившись к пункту главного меню Файл/Сохранить как.
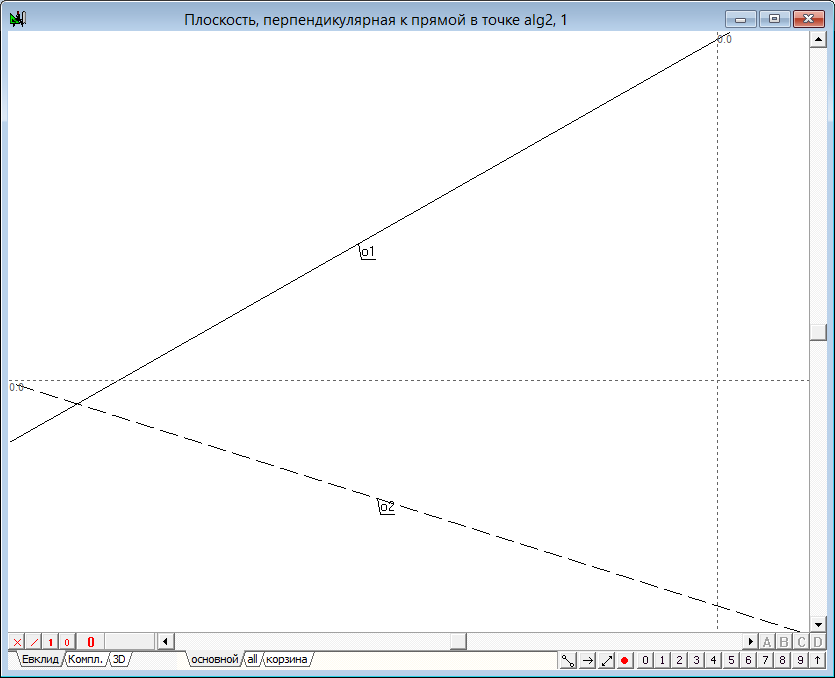
Прямые линии, задающие искомую плоскость, строятся следующим образом:
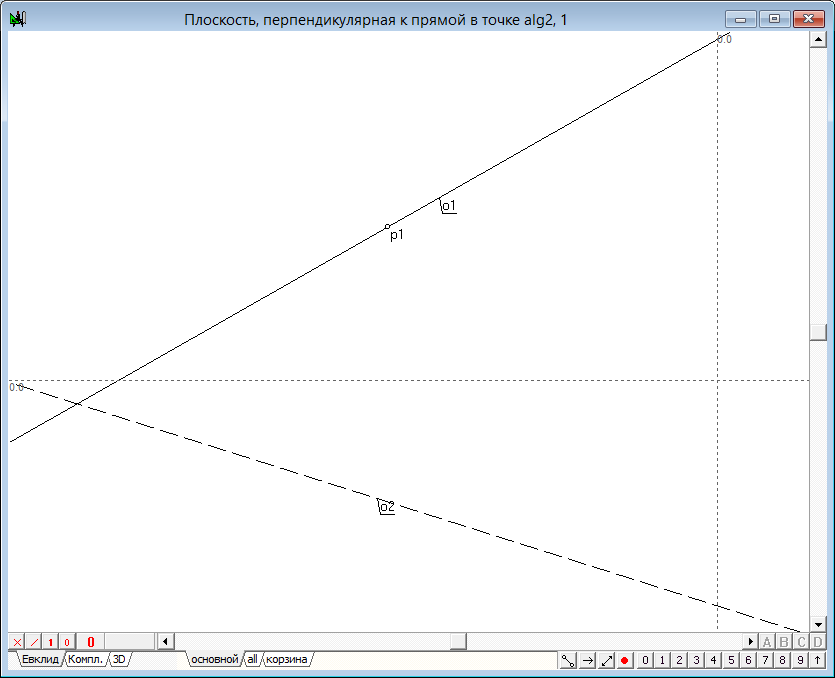
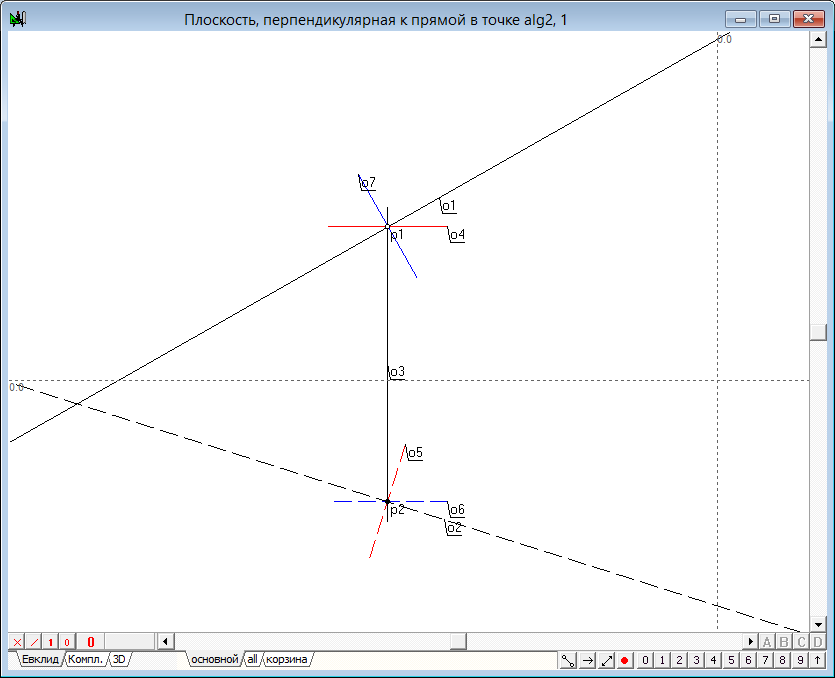
— фронтальная проекция прямой прямой плоскости, перпендикулярной к линии, заданной проекциями o1—o2 должна пройти через точку p1 горизонтально. Для ее построения выделяем точку p1, нажимаем на клавиатуре клавишу с латинским символом h, изменяем атрибут цвета на красный и атрибут начертания на укороченный (клавиша с цифрой 9).
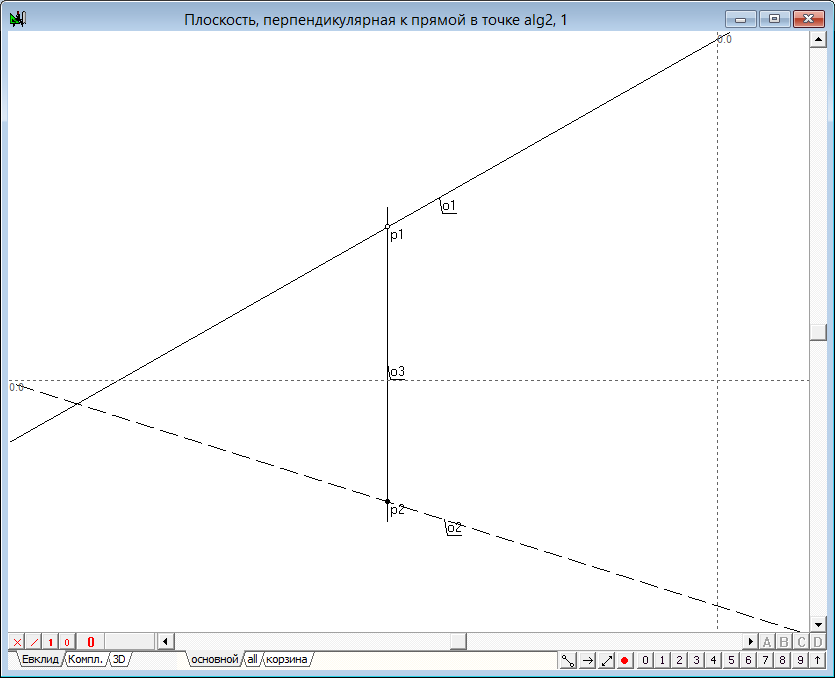
— горизонтальная проекция первой прямой плоскости o5 должна пройти перпендикулярно горизонтальной проекции исходной прямой через точку p2. Для ее построения выделим два объекта — точку p2 и прямую o2 и нажмем на клавиатуре клавишу с латинским символом o. Изменим атрибуты отображения этой прямой.
Проекции второй прямой плоскости строятся по аналогичному правилу лишь с той разницей, что теперь проекция прямой на горизонтальную плоскость должна проходить через точку p2 и быть строго горизонтальной, в то время как фронтальная проекция должна быть перпендикулярной фронтальной проекции исходной прямой и проходить через точку p1.
Реализация алгоритма выполнена. Теперь необходимо определить интерфейс взаимодействия с алгоритмом. Выделим последовательно объекты o4, o5, o7, o6 и, вызвав контекстное меню, назначим их выходными параметрами алгоритма. Вход алгоритма определим следующим образом: Выделим объекты p1, p2, o1, o2 и назначим их входными параметрами алгоритма. Укажем имя алгоритма (Плоскость, перпендикулярная к прямой в точке) и названия входных и выходных параметров.
p1 — 1-я проекция точки;
p2 — 2-я проекция точки;
o1 — 1-я проекция прямой;
o2 — 2-я проекция прямой.
o4 — 1-я проекция 1-ой прямой плоскости;
o5 — 2-я проекция 1-ой прямой плоскости;
o7 — 1-я проекция 2-ой прямой плоскости;
o6 — 2-я проекция 2-ой прямой плоскости.
Приступим к решению основной задачи.
Перейдем в окно алгоритма Главный и разместим в поле чертежа модели четырех точек, расположенных в трехмерном пространстве. Для этого, перемещая курсор по полю чертежа, будем нажимать на клавишу с латинским символом V (верхний регистр). Следует обратить внимание на то, что перед вводом каждой очередной команды необходимо снимать выделение, переводя курсос в поле, свободное от изображений объектов чертежа, и щелкая левой кнопкой мыши.
http://ru.onlinemschool.com/math/formula/sphere/
http://voloshinov.ru/simplex/examples/EX4/index.htm