Уравнение сферы примеры решения задач

Урок «Сфера. Уравнение сферы»

Краткое описание документа:

ТЕКСТОВАЯ РАСШИФРОВКА УРОКА:

Продолжаем изучение сферы.

На прошлых занятиях вы познакомились с определением сферы и шара.

Вспомним, что сферой называется поверхность, состоящая из всех точек пространства, расположенных на заданном расстоянии от данной точки.

Данная точка — центр сферы.

Заданное расстояние — радиус сферы.

Прежде чем вывести уравнение сферы, познакомимся с понятием уравнения поверхности в пространстве.

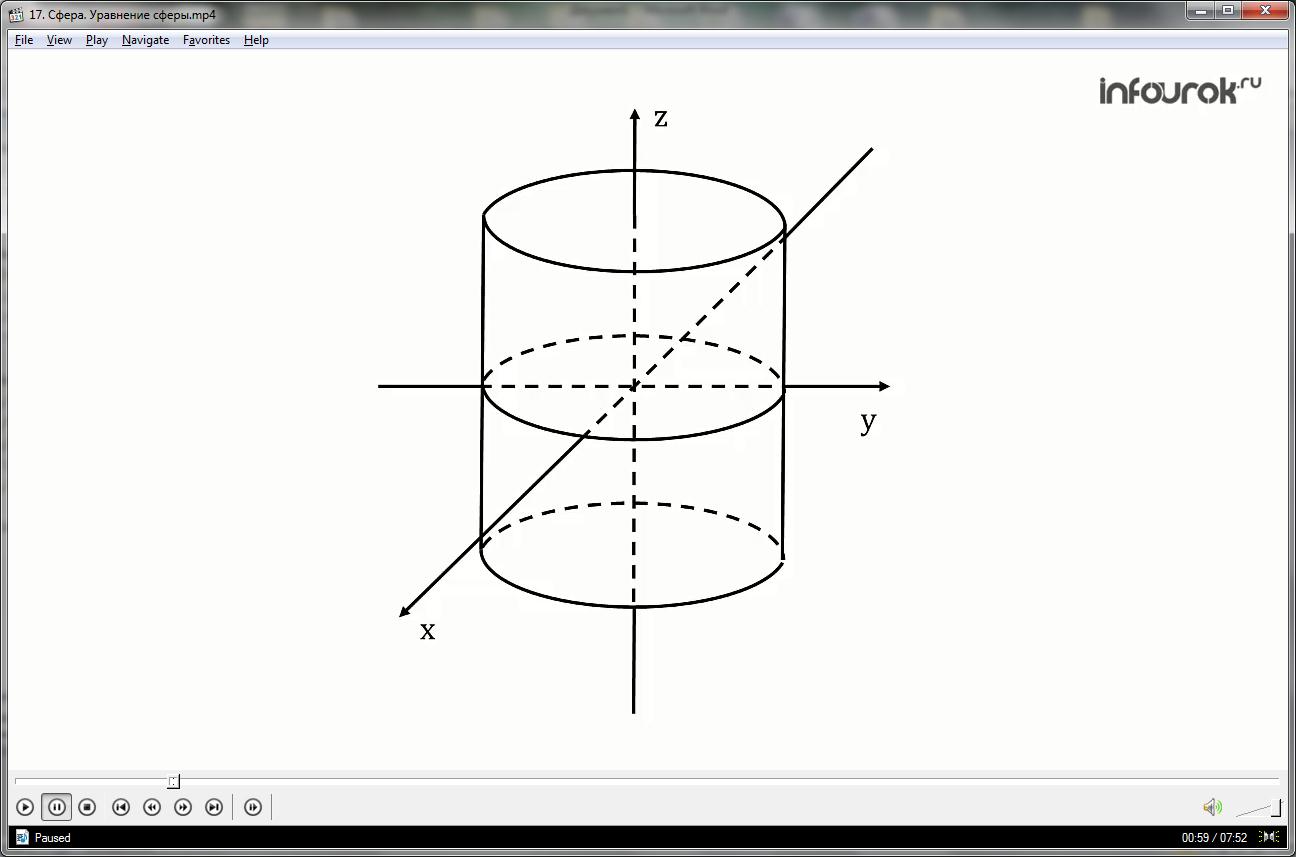
Зададим прямоугольную систему координат Оxyz и некоторую поверхность F.

Уравнением поверхности F называется уравнение с тремя переменными x, y, z, если этому уравнению удовлетворяют координаты всех точек поверхности F и не удовлетворяют координаты точки, не принадлежащей этой поверхности.

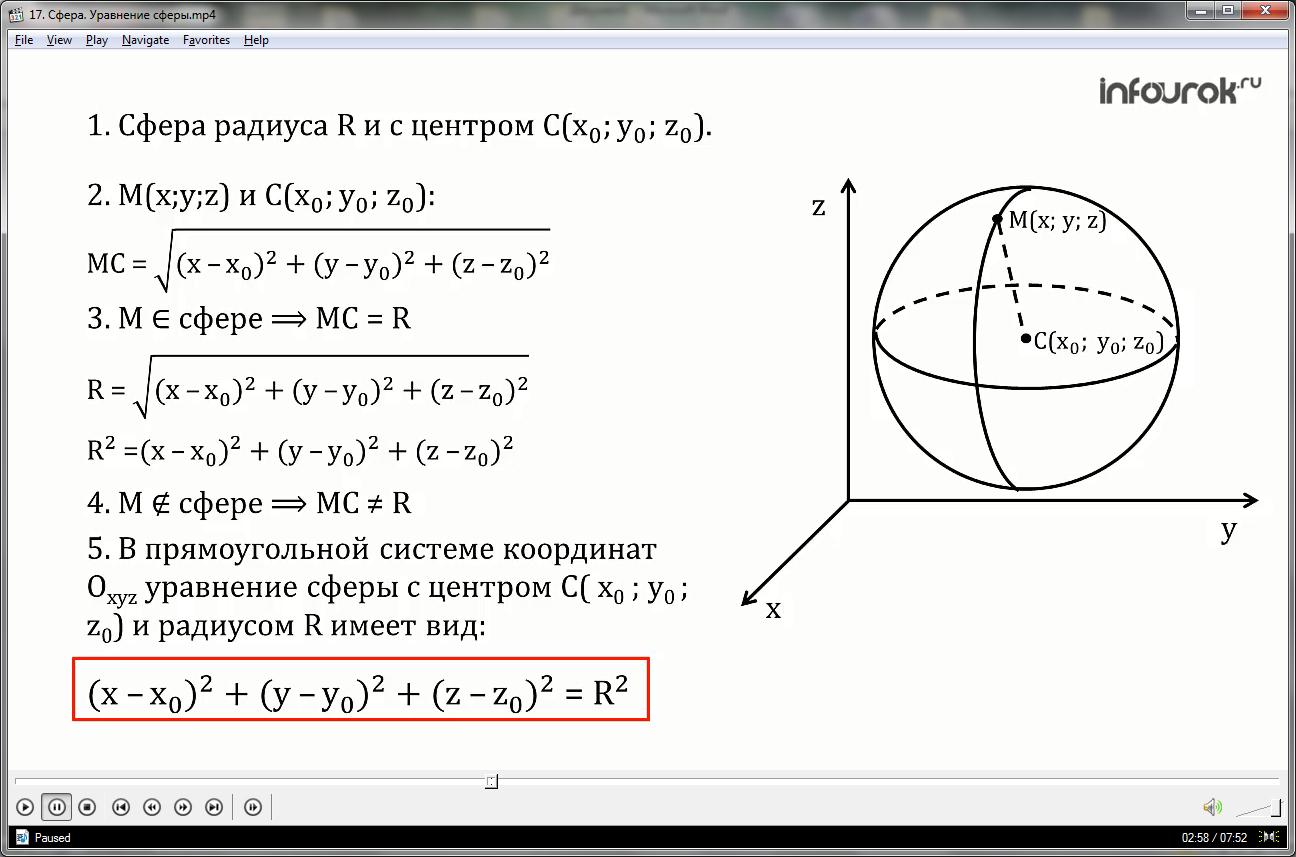
1.Рассмотрим сферу радиуса R и с центром С(x0; y0; z0).

2.Найдём расстояние от произвольной точки М(x; y; z) до центра С( x0 ; y0 ; z0) по формуле для вычисления расстояния между двумя точками с заданными координатами.

3. Если точка М лежит на сфере, то отрезок МС равен радиусу R, то есть

4.В случае если точка М не принадлежит данной сфере, то R≠МС, значит, координаты точки М не удовлетворяют уравнению R2=(x-x0)2+(y-y0)2+(z-z0)2.

5. Таким образом, в прямоугольной системе координат Оxyz уравнение сферы с центром

С (x0 ; y0 ; z0) и радиусом R имеет вид:

Применим полученные знания при решении задач.

Записать уравнение сферы с центром в точке А, которая проходит через точку N, если А(-2;2;0) и N(5;0;-1).

1.Запишем уравнение сферы с центром

А (x0 ; y0 ; z0) и радиусом R:

2.Подставим соответствующие координаты центра сферы А в данное уравнение:

Уравнение сферы с центром в точке А с координатами (-2;2;0) примет вид:

3.Так как сфера проходит через точку N с координатами (5;0;-1), то её координаты удовлетворяют уравнению сферы, подставим координаты этой точки в полученное уравнение:

Таким образом, уравнение сферы с центром в точке А, которая проходит через точку N имеет вид:

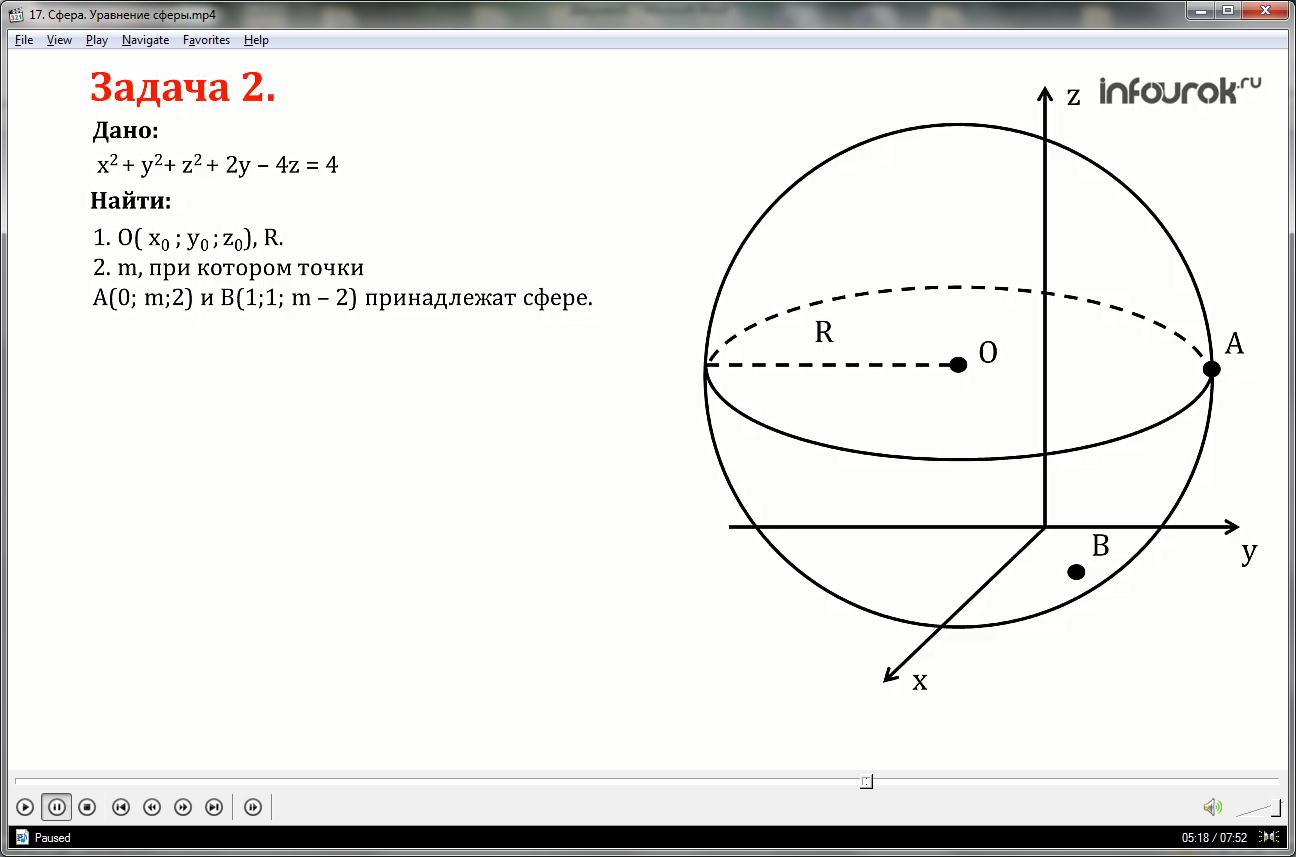
Сфера задана уравнением:

1) Найти координаты центра и радиус сферы;

2) Найти значение m, при котором точки

А (0; m;2) и В (1;1; m-2) принадлежат данной сфере.

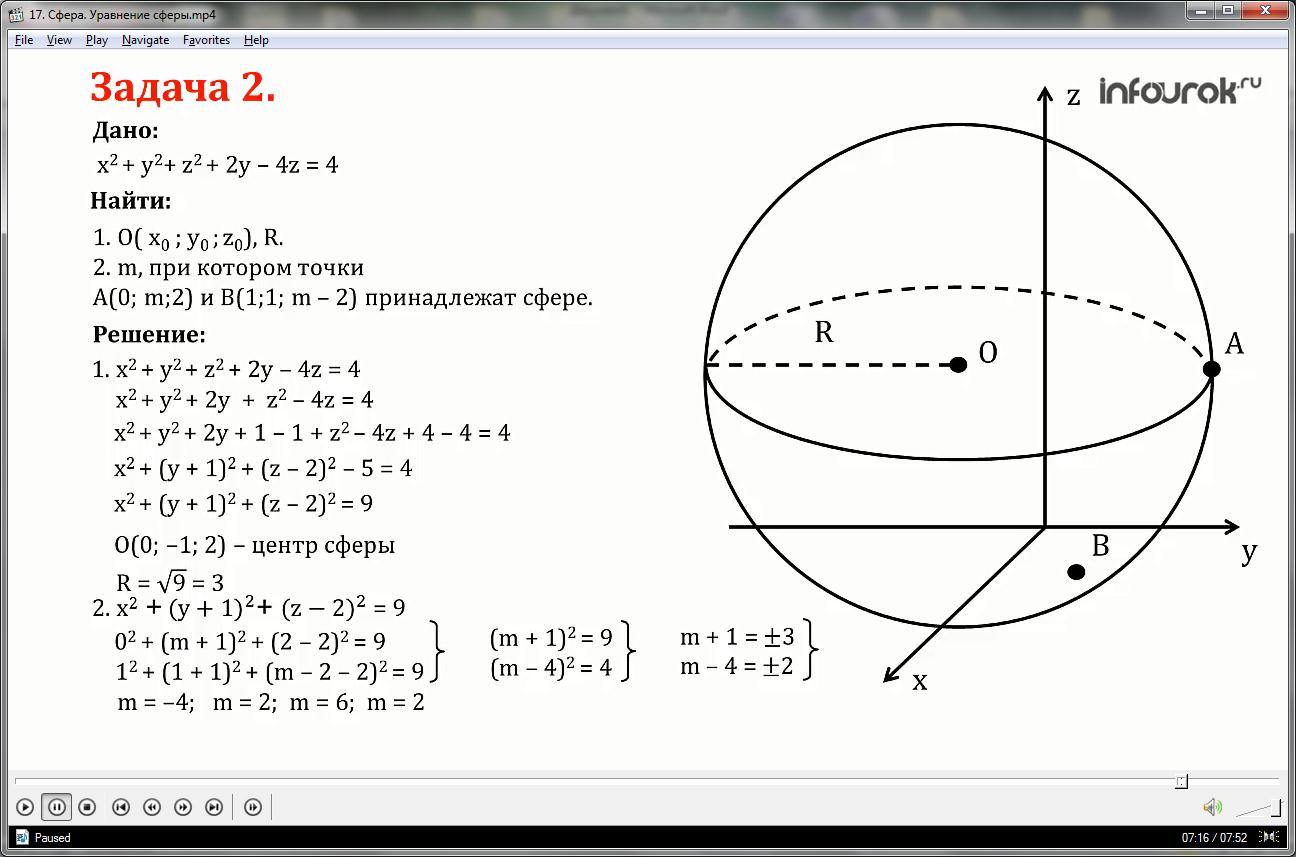
1. Уравнение данной сферы имеет вид:

x2+ y2+ z2+2y-4z=4 или x2+ y2+2y + z2-4z=4

Выделим полный квадрат для переменных y и z, для этого прибавим и одновременно вычтем 1 и 4 в левой части уравнения:

x2+ y2+2y+1-1 + z2-4z+4-4=4

Уравнение примет вид:

x2+( y+1)2+( z-2)2-5=4 или

Таким образом, центр сферы имеет координаты:

О (0;-1;2), радиус равен R=√9=3

2.Уравнение сферы с центром в точке О (0;-1;2) и радиусом R=3 имеет вид:

Точки А (0; m;2) и В (1;1; m-2) принадлежат данной сфере, значит их координаты удовлетворяют уравнению сферы. Подставим координаты этих точек в уравнение сферы и решим систему уравнений:

Упростим полученные уравнения, раскрывая скобки и приводя подобные слагаемые:

Таким образом, мы получили 4 значения m:

Несложно проверить, что при m=-4 и m=6 координаты точек А и В не удовлетворяют уравнению сферы. Проверьте самостоятельно.

Итак, при m=2 точки А (0; m;2) и В (1;1; m-2) принадлежат сфере, заданной уравнением

x2+ y2+ z2+2y-4z=4 с центром в точке

О (0;-1;2) и радиусом R=3.

—> —>

АвторДата добавленияРазделПодразделПросмотровНомер материала

Инфоурок

07.11.2014

Геометрия

Видеоурок

51692

1003

© 2022 Проект «Уроки математики»

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено!

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако команда проекта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом на электронную почту службы поддержки сайта.

Урок геометрии на тему «Сфера и шар. Уравнение сферы». 11-й класс

Разделы: Математика

Класс: 11

Цель: Определение шара и сферы (шаровой поверхности) и связанных с ним понятий (центр, радиусы, диаметры, диаметрально противоположные точки). Рассмотреть уравнение сферы.

Оборудование: плакаты, модели шара, сферы.

2) Проверка домашнего задания.

3) Повторить определение окружности, уравнение окружности. Решить устно две задачи.

2. Изучение нового материала.

1) Определение сферы и шара (на моделях и рисунках) №574 (а).

2) Уравнение сферы.

3) Решение устных примеров.

3. Закрепление материала. № 576 (а), 576 (б)-С, 578 (г), 577 (а), 579 (а, б)

4. Домашнее задание: параграф 3. П 58,59. №576 (б), 577 (б), 579(в, г), 574(б).

6. Решение задач повышенной сложности.

1) Организационный момент

2) Проверка домашнего задания.

3) Учитель: Ребята, вам на дом было повторить определение окружности, круга, расстояние между двумя точками в пространстве. Уравнение окружности.

Показываю плакат окружности, круга и повторяем определение.

Ученики:

Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки.

Круг – часть плоскости, ограниченная окружностью.

Учитель: Напишите, пожалуйста, на доске уравнение окружности (x-x₀) 2 + (y-y₀) 2 = R 2 , где (x₀; y₀)- центр окружности, R- радиус, (x; y)- координата центра окружности.

Устно. Найти уравнение окружности?

1) (x-4) 2 +(y-3) 2 =9. 2) x 2 + y 2 =4. 3) (0-4) 2 +(0-3) 2 =R 2 . 4) 16+9=R 2 .

5)25=R 2 . 6) R=5. 7)(x+4) 2 +(y-3) 2 =25.

Учитель: Найдите расстояние М₁ М₂, если М₁ (-3; 0; 4), М₂ (0; 6; 5). М₁ М₂ = (0-3) 2 + (6-0) 2 +(5-4) 2 = 46.

Следовательно, d= (x-x) 2 +(y-y) 2 + (z-z) 2 .

2. Объяснение нового материала. Сфера.

1) Учитель: Геометрия изучает форму и взаимное расположение фигур в пространстве. Мы живем в мире трех измерений.

Окружность и круг это пространственные тела или плоские?

В какое геометрическое тело превратится окружность (круг), если попадет в пространство?

Ученики: В сферу и шар.

Учитель: (показывает плакаты) Остановимся на сфере.

1). Сферу можно получить вращением полуокружности вокруг ее диаметра как оси.

2). Границы шара называется шаровой поверхностью или сферой.

3). Сферой называется поверхность, состоящая из всех точек пространства, расположенных на данном расстоянии от данной точки.

Обозначение. (Рассказываю с помощью плаката) : Радиус, диаметр, центр сферы D=2R, обозначение сферы .

1. Шар — может быть получен вращением полукруга вокруг диаметра как оси.

2. Шаром называется тело, ограниченное сферой.

3. Шаром называется тело, которое состоит из всех точек пространства, находящихся на расстоянии, не большем данного, от данной точки.

Эта точка называется Центром шара. А данное расстояние – радиусом шара. Отрезок соединяющий две точки шаровой поверхности проходящей через ее центр – называется диаметром.

А теперь запишем число, тему: п. 48. Шар. Сфера.

В тетрадях рисуем один чертеж, пишем определения и обозначения. Пишем три определения шара и сферы. (под диктовку)

3. Закрепление. №574 (а, б)

Дано: сфера, т О — центр, R — радиус т.А и В € . а) R= 50 см, АВ= 40 см б) R=15 мм, АВ=18 мм.

Найти: ОМ.

Решение. а) ОА=ОВ= R=50 см. Следовательно треугольник АОВ — равнобедренный —> ОМ — высота (по свойству медианы в равнобедренном треугольнике). Рассмотрим треугольник АОМ (LО=90 0 ). По теореме Пифагора

ОМ= v АО 2 – АМ 2 = v 2500-400 = v 2100 =10 v21 (см).

Самостоятельно б) ОМ= v 225-81 = v 144= 12 (мм) Ответ: 10 v21 см; 12 мм.

Уравнение сферы. П 59.

Пусть задана прямоугольная система координат Охуz и дана некоторая поверхность. Уравнение с тремя переменными х, у, z, называется уравнением поверхности, если этому уравнению удовлетворяют координаты любой точки F и не удовлетворяют координаты никакой точки не лежащей на этой поверхности.

Дано: прямоугольная система координат Охуz сфера , h – радиус точка С (х₀, у₀, z₀) — центр сферы.

Написать уравнение сферы.

Решение: Возьмем произвольную т М (x;y;z). Расстояние от М до С, МС= v (x-x₀) 2 +(y-y₀) 2 + (z-z₀) 2 если точка М € , то МС= R или МС 2 = R 2 , т.е. координаты т. М удовлетворяют уравнению

Если М € , то МС 2 = R 2 и координаты (т. М) не удовлетворяют уравнению. Следовательно, в прямолинейной системе координат уравнение сферы радиуса R с центром С(х₀, у₀, z₀) имеет вид

5. Закрепление по теме: уравнение сферы №576(а, б), 578, 577 (а).

№576. Напишите уравнение сферы радиуса R с центром в центре А, если а) А(2;-4; 7), R=3.

Ответ (x-2) 2 +(y+4) 2 + (z-7) 2 =9 2 .

Б) А(0;0;0) R= v 2. Ответ: x 2 +y 2 + z 2 =2.

№578 а) А(0;0;0) , R=7. Б) А(3; -2; 0), R= v 2.

№577 а) Дано: сфера , т. А — центр, N= ?, А(-2; 2; 0), N(5; 0; -1)

Найти: уравнение сферы.

(5-2) 2 +(0-2) 2 + (-1-0) 2 = R 2 .

(x+2) 2 +(y-2) 2 + z 2 =54.

Учитель: Ребята, как записывается уравнение сферы, если ее центр лежит в т (х₀, 0, 0), а радиус равен R.

(x-x₀) 2 +y 2 + z 2 =R 2 .

x 2 — 2xx₀+x₀ 2 +y 2 +z 2 = R 2 .

x 2 — 2xx₀ +y 2 +z 2 = R 2 -x₀ 2 — уравнение сферы.

Уравнение сферы примеры решения задач

Глава VI. Простейшие криволинейные поверхности и тела вращения.

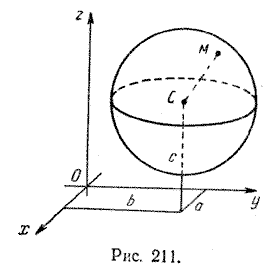
Множество всех точек пространства, находящихся на данном расстоянии R от данной точки С, называется сферой радиуса R с центром в точке С (рис. 211).

Другими словами, сфера радиуса R с центром в точке С — это множество всех точек М пространства, удовлетворяющих условию

Отрезок, соединяющий две точки сферы и проходящий через ее центр, называется диаметром сферы. Очевидно, что длина диаметра сферы радиуса R равна 2R.

Если в пространстве задана некоторая прямоугольная декартова система кородинат и
(а; b; с) — координаты точки С, а (х; у; z) — координаты точки М, то условие (1) принимает вид

Отсюда следует, что сфера радиуса R с центром в точке С (а; b; с) имеет уравнение

(x — a) 2 + (y — b) 2 + (z — c) 2 = R 2 (2)

B частности, сфера радиуса R с центром в начале координат имеет уравнение

Задача 1. Составить уравнение сферы радиуса R = 5 с центром в начале координат.

Непосредственной подстановкой значения радиуса в уравнение (3) получим

Задача 2. Написать уравнение сферы с центром в точке С (2; —3; 5) и радиусом, равным 6.

Подставив значение координат точки С и значение радиуса в уравнение (2), получим

(x — 2) 2 + (y + 3) 2 + (z — 5) 2 = 36.

Задача 3. Найти центр и радиус сферы

Сравнивая данное уравнение с уравнением сферы (2), видим, что
а = — 4, b = 3, с = 0, R = 10. Следовательно, С(—4; 3; 0), R = 10.

Задача 4. Доказать, что уравнение

является уравнением сферы.

Преобразуем левую часть данного уравнения, выделив квадраты двучленов, содержащих соответственно х, у и z:

Следовательно, данная поверхность имеет уравнение

Это уравнение представляет собой уравнение сферы с центром в точке С(1; —2; 3) и радиусом R = 3.

Множество всех точек пространства, расстояние которых от данной точки С не превосходит данного числа R, называется шаром радиуса R с центром в точке С.

Иначе, шар радиуса R с центром в точке С — это множество всех точек М пространства, удовлетворяющих условию

Сфера радиуса R с центром в точке С называется поверхностью соответствующего шара. Про нее говорят, что она ограничивает шар радиуса R с центром в точке С.

Теорема. Через любые четыре точки, не лежащие в одной плоскости, проходит и притом единственная сфера.

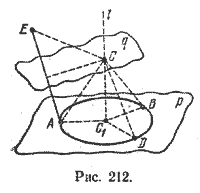
Пусть А, В, D, Е четыре точки, не лежащие в одной плоскости. Достаточно доказать, что существует и притом единственная точка, С, равноудаленная от четырех данных точек. Очевидно, точка С и будет центром сферы, проходящей через данные точки.

Через точки А, В, D, которые, очевидно, не лежат на одной прямой, проходит единственная плоскость р и единственная окружность. Пусть С₁ — центр этой окружности. Очевидно, множество всех точек пространства, равноудаленных от трех точек А, В, D — это перпендикуляр l к плоскости р, проходящий через точку C₁ (рис. 212).

Рассмотрим теперь точки А и Е. Множество всех точек пространства, равноудаленных от точек А и Е, — это плоскость q, перпендикулярная прямой АЕ и проходящая через середину отрезка АЕ. Плоскость q обязательно пересечет прямую l , так как точка Е не лежит в плоскости р. Очевидно, что точка С, являющаяся пересечением плоскости q с прямой l, будет равноудаленной от всех четырех данных точек А, В, D, Е. Из построения видно, что точка С — единственная точка пространства, удовлетворяющая этому условию.