Уравнение сферы в полярной системе координат

Уравнение сферы в полярной системе координат

Для определения координат в декартовой системе координат используются координатные оси. Однако в ряде случаев удобно в качестве координат использовать не метрические величины, а величины других размерностей, например, углы.

Полярная система координат ставит в соответствие каждой точке на плоскости пару чисел Основными понятиями этой системы являются точка отсчета – полюс – и луч, начинающийся в этой точке, – полярная ось . Координата ρ – расстояние от точки до полюса, координата φ – угол между полярной осью и отрезком, соединяющим полюс и рассматриваемую точку, который берется со знаком «+», если угол от оси до отрезка вычисляется против часовой стрелки, и со знаком «–» в противоположном случае. Важно понимать, что число φ в полярной системе определено не однозначно: парам чисел (ρ; φ + 2π) соответствует одна и та же точка при любых натуральных . Для полюса , а угол φ не определен.

Рисунок 1.2.2.1.

Полярные координаты легко преобразовать в декартовы. Пусть – координаты точки в декартовой системе координат, – в полярной. Тогда очевидно, что

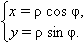Формулы обратного перехода:

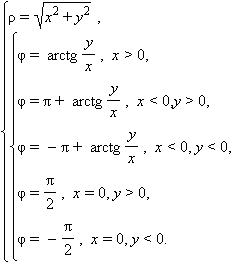Полярную систему можно обобщить на трехмерный случай: для этого придется ввести третью координату – угол θ. Углы φ и θ примерно соответствуют земным долготе и широте (угол θ также отсчитывается от «экватора»), а координата ρ определяет расстояние от исследуемой точки до полюса. Подобная система координат носит название сферической . Сферическими координатами точки в трехмерном пространстве являются:

• ρ – расстояние от точки до полюса,
• φ – угол между полярной осью и проекцией радиус-вектора точки на выбранную экваториальную плоскость (содержащую полярную ось),
• θ – угол между радиус-вектором точки и его проекцией на экваториальную плоскость.

Система координат, состоящая из полюса, экваториальной плоскости и полярной оси, лежащей в ней, называется сферической .

Математический портал

Nav view search

Navigation

Search

• Вы здесь:
• Home
• Векторная алгебра.
• Высшая математика.
• Векторная алгебра.
• Полярная, цилиндрическая и сферическая системы координат. Формулы перехода.

Полярная, цилиндрическая и сферическая системы координат. Формулы перехода.

Полярные координаты.

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.

$$x=\rho \cos\varphi,\; y=\rho\sin\varphi,\quad (\rho\geq 0,\,\,\,0\leq\varphi\leq 2\pi)$$

Обобщённые полярные координаты.$$ x=a\rho\cos\varphi,\; y=b\rho\sin\varphi,\quad (\rho\geq0, 0\leq\varphi\leq 2\pi)$$

Цилиндрические координаты:

Цилиндрической системой координат называют трёхмерную систему координат , являющуюся расширением полярной системы координат путём добавления третьей координаты (обычно обозначаемой ), которая задаёт высоту точки над плоскостью.

$x=\rho\cos\varphi,\;y=\rho\sin\varphi,z=h,$ $ (\rho\ge 0,\, 0\le\varphi\le 2\pi,\, -\infty

Сферические координаты.

Положение точки М в сферической системе координат задается тройкой чисел r , φ и θ, где r – расстояние от начала координат до точки M ( ); φ – угол, образованный проекцией радиус-вектора на плоскость О ху с положительным направлением оси О х ( ); θ – угол между положительным направлением оси O z и радиус-вектором точки М ( ).

$$\left\<\begin x=r\cos\varphi\cos\theta,\\ y=r\sin\varphi\cos\theta,\\ z=r\sin\theta,\end\right.$$

$ (r\geq 0,\;0\leq\varphi \leq 2\pi,\; -\frac<\pi><2>\le\theta\le\frac<\pi><2>).$

Обобщённые сферические координаты.

$$ \left\<\begin x=ar\cos^\alpha\varphi\cos^\beta\theta,\\ y=br\sin^\alpha\varphi\cos^\beta\theta,\\ z=cr\sin^\beta\theta, \end \right. $$

Сферические координаты (сферическая система координат)

Для введения сферической системы координат в пространстве выбирается плоскость ( основная плоскость ) и на ней задается полярная система координат с полюсом ( начало сферической системы координат ) и полярной осью . Через точку перпендикулярно основной плоскости проведем ось ( ось аппликат ) и выберем ее направление так, чтобы возрастание полярного угла со стороны положительного направления оси происходило против часовой стрелки (рис.2.36,а).

В сферической системе координат положение точки , не лежащей на оси аппликат, характеризуется расстоянием до начала координат, полярным углом точки — ортогональной проекции точки на основную плоскость, и углом между вектором и положительным направлением оси аппликат. Таким образом, сферические координаты точки — это упорядоченная тройка чисел – радиус , долгота и широта . У точек, принадлежащих оси аппликат, не определена долгота, их положение задается радиусом и широтой для положительной части оси и для отрицательной ее части. Начало координат задается нулевым значением радиуса . Иногда вместо угла широтой называют угол , принимающий значения .

Со сферической системой координат можно связать прямоугольную систему координат (рис.2.36,б), у которой начало и базисные векторы совпадают с началом сферической системы координат и единичными векторами на полярной оси и оси аппликат соответственно, а базисный вектор выбирается так, чтобы тройка была правой (при этом базис оказывается стандартным).

Наоборот, если в пространстве задана правая прямоугольная система координат, то, приняв положительную полуось абсцисс за полярную ось, получим сферическую систему координат ( связанную с данной прямоугольной ).

Переход от сферических координат к декартовым (прямоугольным)

Получим формулы, связывающие между собой прямоугольные координаты точки и её сферические координаты . По рис.2.36,б получаем

Эти формулы перехода позволяют найти прямоугольные координаты по известным сферическим координатам. Обратный переход выполняется по формулам

Формулы (2.22) определяют долготу с точностью до слагаемых , где . При из них следует, что . Главное значение долготы находится по формулам (см. рис.2.29).

Пример 2.13. В сферической системе координат :

а) построить координатные поверхности ;

б) найти сферические координаты точки , если известны её прямоугольные координаты ;

в) найти прямоугольные координаты точки , если известны её сферические координаты: .

Решение. а) Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении радиуса , является сфера с центром в начале координат (рис.2.37). Этим объясняется название сферической системы координат. Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении долготы , является полуплоскость, ограниченная осью аппликат (на рис.2.37 изображена полуплоскость ). Координатной поверхностью , т.е. геометрическим местом точек при фиксированном значении широты , является конус, ось которого совпадает с осью аппликат, а вершина — с началом координат. При получаем основную плоскость. На рис.2.37 изображены конус и основная плоскость .

б) Найдем сферические координаты точки . По формулам (2.22), учитывая рис.2.29 (см. пример 2.12), получаем