Уравнение шредингера для свободной микрочастицы
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
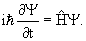 | (4.1) |
где 
в которой 







х → 


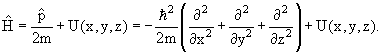 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


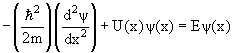
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
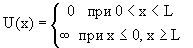 | (4.5) |
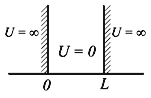
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
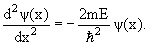 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
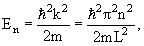 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
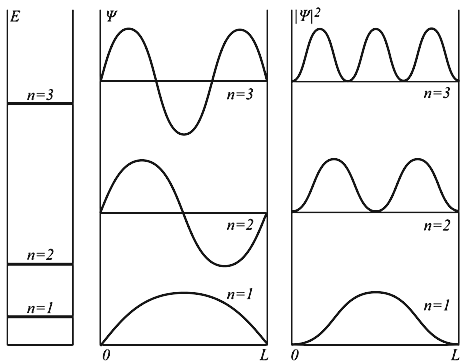
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
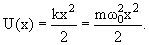 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
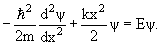 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
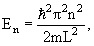

Одномерный гармонический осциллятор:
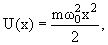
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
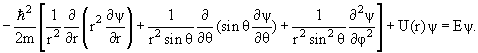 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
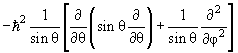 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 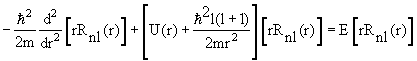 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
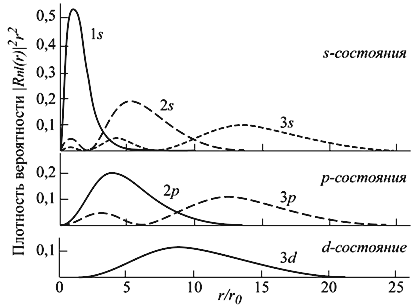
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
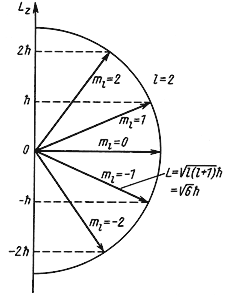
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
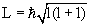 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
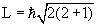
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Соотношение неопределенности, волновая функция, излучение и поглощение энергии
Конспект лекции
Аннотация: знакомство с границами применимости классической физики, уравнением Шредингера. Традиционное изложение темы.
В первой четверти XX-го века получены экспериментальные свидетельства двойственности свойств материи: электромагнитное излучение проявляет свойства частиц (фотоэффект, комптоновское рассеяние, . ), а частицы демонстрируют волновые свойства (эффект Рамзауэра, туннельный эффект, . ).
Но свойства волн и частиц в известной степени противоположны.
| Частицы | Волны |
|---|---|
| Энергия и импульс локализованы | Переносят энергию, распределенную по фронту волны |
| Сложение по правилу: частицы + частицы => больше частиц | Интерференция лучей: больше в одном месте и меньше в другом |
| Отбрасывают резкую тень | Огибают препятствия |
| При наличии щелей частица проходит через одну из них | Проходят через любое число отверстий |
Нет подходящих образов, чтобы представить существование волновых и корпускулярных свойств у одного объекта. Нельзя все свойства волн и все свойства частиц приписать одному объекту. Необходимо внести некоторые ограничения в применении к объектам микромира понятий классической физики. Корпускулярно-волновая двойственность свойств частиц, изучаемых в квантовой механике, приводит к тому, что в ряде случаев оказывается невозможным, в классическом смысле, одновременно характеризовать частицу ее положением в пространстве (координатами) и скоростью (или импульсом). В 1927 году немецкий физик Вернер Гейзенберг сформулировал принцип неопределенности, названный теперь его именем. Он может быть записан в следующем виде

Здесь Δx — неопределенность координаты x, Δp — неопределенность импульса, ħ — постоянная Планка, деленная на 2π (h = 6.62·10 -34 Дж·с). Выражение (1) следует понимать так, что если мы точно задаем координату частицы (Δx → 0), то ничего не можем сказать о величине импульса (Δp → ∞). Одновременно точно задать координату и импульс микрочастицы невозможно. Для иллюстрации рассмотрим опыт по дифракции электронов на щели. Прямой опыт Йенсона (см. лекцию) показал, что за щелью распределение интенсивности электронов будет иметь вид, показанный на рис.1. 
Отклонение электрона от первоначального направления означает получение им приращения импульса Δp. Ширина щели служит мерой неопределенности положения электрона (электрон проник в щель, в какой точке щели это произошло, неизвестно). Из опыта известно, что при уменьшении ширины щели дифракционная картина уширяется. Т.е., если Δx уменьшается, Δp растет, как это предсказывает соотношение (1).
Принцип неопределенности не мешает нам с любой желаемой точностью измерить каждую из величин, входящих в соотношение. Он утверждает лишь, что мы не в состоянии достоверно узнать и то, и другое одновременно. Неравенства (1) и (2) представляют собой ограничения применимости понятий классической механики.
Оценим количественную сторону ограничений на трех примерах.
- Молекула в стакане.
Массы молекул имеют порядок 10 -27 кг. Пусть стакан имеет размер
10 -1 м. Эту величину возьмем в качестве неопределенности координаты Δx. Тогда для неопределенности скорости получим

Чрезвычайно малое значение Δv в сравнение со скоростью молекул (при комнатной температуре порядка 500 м/с) приводит к выводу об отсутствии ограничений на классическое рассмотрение движения молекул в этом случае.
Электрон в атоме.
10 -30 кг, размер атома
10 -10 м. Для неопределенности скорости получим

И поскольку эта величина Δv сравнима со скоростью электронов в атоме, соотношение неопределенностей играет решающую роль, игнорировать волновые свойства электрона никак нельзя.
Луч осциллографа.
Скажутся ли волновые свойства электрона на работе осциллографа? Пусть радиус луча на экране очень качественного осциллографа равен r = 10 мкм, длина трубки L
10 -1 м. Тогда относительное изменение импульса Δp/p = r/L = 10 -4 . Импульс электрона определим, задав напряжение на трубке U, равным 10 кВ

Неопределенность импульса тогдаΔp
6·10 -27 , а неопределенность координаты
что существенно меньше размера пятна на экране. Т.е. пользоваться осциллографом можно, не задумываясь о волновых свойствах электронов.
Приведем один пример использования соотношения неопределенностей для оценки физических величин. Исходим из того, что неопределенность, например, импульса — это минимальное значение импульса, которое что-то значит.
Покажем, что в существующих ядрах не могут находиться электроны. За неопределенность координаты возьмем радиус ядра r, тогда
Размеры ядер имеют порядок 10 -14 м, электрон с таким импульсом — ультрарелятивистский, его энергия много больше энергии покоя, и последней можно пренебречь в оценках. Имеем E = p·c (как для фотонов). Для того чтобы электрон находился в ядре, его кинетическая энергия должна быть меньше потенциальной энергии (энергии взаимодействия с заряженным шаром, которым представляем ядро). Получаем
Ядер с таким большим атомным номером не существует. Точное решение задачи с нахождением волновой функции показывает отсутствие связанного состояния для электрона в потенциальной яме, которой представляется ядро.
Другая важная пара связанных физических величин – энергия Е и время t. Соотношение неопределённостей для них имеет вид

Если под величиной Δt понимать среднее время жизни атома в возбужденном состоянии, то энергия этого состояния определена с точностьюΔE. В основном состоянии атом может находиться без внешних воздействий бесконечно долгое время: Δt = ∞. Тогда ΔE = 0, то есть в основном состоянии энергия атома является строго определенной величиной. Однако каждый возбужденный уровень энергии имеет конечную ширину, которая определяется временем жизни атома в этом состоянии. Вследствие этого длина волны испускаемого кванта при переходе из возбужденного состояния не будет однозначной, спектральная линия излучающего атома имеет конечную ширину. Говорят о естественной ширине линии. Ширина спектральной линии определяется шириной уровней энергии, между которыми происходит переход. Обычно ширина уровней энергии очень мала. Например, для переходов с излучением в видимой части спектра (время жизни атома в возбужденном состоянии
Соотношение (2) допускает рождение на короткое время с последующим исчезновением частиц (их называют виртуальными (возможными) частицами). Их время жизни очень мало — порядка 10 -21 — 10 -24 с. Это объясняет, почему в вакууме постоянно присутствуют кванты различных полей. Отдельные виртуальные частицы нельзя обнаружить в принципе, но их суммарное воздействие на обычные микрочастицы обнаруживается экспериментально. В опыте У.Лэмба и Р.Ризерфорда (1947 г.) при исследовании спин-орбитального расщепления (см. лекцию) 2p уровня атома водорода обнаружено не только ожидаемое расщепление энергий состояний 2p3/2 и 2p1/2, но и отличие энергий 2s1/2 и 2p1/2 состояний. Это отличие обусловлено, как выяснилось позднее, во-первых, испусканием и поглощением связанным электроном виртуальных фотонов, что приводит к изменению эффективной массы электрона и возникновению у него аномального магнитного момента, и, во-вторых, возможностью виртуального рождения и аннигиляции в вакууме электронно-позитронных пар, что искажает кулоновский потенциал ядра. Лэмбовский сдвиг оказался первым физическим эффектом, на котором подтвердилась правильность квантовой электродинамики.
Волновая функция
Наличие волновых свойств у микрочастицы показывает, что ей (микрочастице) следует сопоставить некоторое волновое поле (аналог знакомых нам электрического, магнитного, гравитационного полей). Амплитуду этого волнового поля, зависящую от координат и времени, принято называть волновой функцией 
величина 
Вспомним опыт с пропусканием электронов через щель. Куда попадет данный конкретный электрон — дело случая. После пропускания малого числа электронов картина похожа на мишень плохого стрелка. Поведение электрона должно описываться некоторой вероятностной функцией. И эта функция должна быть связана со свойствами волнового поля, т.к. итог большого числа попаданий электронов — вполне четкая картина дифракционных полос. Совместить случайный характер попадания электрона в данное место с его волновыми свойствами можно, лишь допустив, что вероятность попадания электрона в данную точку пропорциональна интенсивности волнового поля, т.е. квадрату амплитуды |Ψ| 2 . |Ψ| 2 имеет смысл плотности вероятности. С помощью волновой функции можно рассчитать все измеряемые физические характеристики системы частиц. Например, среднее расстояние электрона от ядра
Свойства волновой функции:
- самое главное — сама амплитуда Ψ(x,y,z,t) непосредственного физического смысла не имеет; только |Ψ| 2 — плотность вероятности;
- волновая функция может быть комплексной (так чаще всего и бывает);
- умножение волновой функции на постоянную величину не изменяет физического состояния частицы, которая она описывает (распределение вероятности в пространстве и во времени не изменится; во сколько раз частицу чаще можно встретить в одной точке, чем в другой, во столько же раз и после умножения);
- волновая функция должна быть непрерывной и однозначной;
- непрерывной должна быть и первая производная по координате, так как через нее определяется импульс частицы;
- волновая функция не должна обращаться в бесконечность;
- обычно волновую функцию нормируют так ,что
т.е. вероятности достоверного события.
Уравнение Шредингера
Уравнение, решением которого является волновая функция, получено австрийским физиком Э.Шредингером
- m — масса частицы;
- Ψ(x,y,z,t) — волновая функция;
- ħ — постоянная Планка, деленная на π2;
— оператор Лапласа;
- U(x,y,z,t) — потенциальная энергия;
- i — мнимая единица.
Это уравнение применимо только для нерелятивистских частиц, у которых масса не зависит от скорости.
Для многих задач уравнение Шредингера можно упростить, исключив зависимость от времени. Это так называемые стационарные задачи. Пусть потенциальная энергия зависит только от координат U = U(x,y,z). Будем искать решение в виде произведения двух функций, зависящих одна от координат, а другая от времени: Ψ(x,y,z,t) = ψ(x,y,z)·φ(t). Поставим это выражение в уравнение и вынесем из-под знаков дифференцирования сомножители, не зависящие от соответствующих переменных
Разделим получившееся уравнение на ψ(x,y,z)·φ(t). Теперь левая часть зависит только от координат, а правая от времени. Поскольку обе части равны между собой, то остается единственная возможность: каждая из них равна одной и той же константе. Обозначим эту константу -E (E, как будет видно, — полная энергия частицы).
Теперь имеем два уравнения: первое для функции ψ(x,y,z)
Это так называемое стационарное уравнение Шредингера. Второе, которое легко решается, для временной части
Итак, для стационарного случая имеем два дифференциальных уравнения. Многочисленные эксперименты подтверждают выводы, вытекающие из решения уравнения Шредингера. На этом основана наша уверенность в справедливости этого уравнения.
В 1933г. Эрвину Шредингеру присуждена Нобелевская премия:
E RWIN S CHRODINGER for the discovery of new productive forms of atomic theory.
(за открытие новых продуктивных форм атомной теории)
Решение уравнения Шредингера для свободной частицы
Для понимания природы явлений в микромире обычно достаточно решить одномерную задачу. Этим мы и займемся. Для свободной частицы U(x) = 0, и уравнение Шредингера имеет вид

Имеем дифференциальное уравнение второго порядка с посто39янными коэффициентами. Его решение, используя характеристическое уравнение, получаем в виде

Теперь добавим множитель φ(t), зависящий от времени (см. выше)

Если учесть, что E/ħ = ω, получили уравнение волны с фазой kx-ωt в первом слагаемом и -kx-ωt во втором. Если фазу зафиксировать, то точка с постоянной фазой движется в направлении x для первого слагаемого (x растет с увеличением t), и в противоположном для второго. Первое слагаемое описывает движение частицы в направлении x, второе — против x.
Выражение (4) однозначно, конечно и имеет смысл при любых значениях энергии E. Энергия свободной частицы может принимать любое значение, т.е. ее энергетический спектр является непрерывным.
Этой волне соответствует не зависящая от времени вероятность обнаружить частицу в данной точке пространства. Действительно, выбирая для простоты волну, распространяющуюся в положительном направлении x, имеем |Ψ| 2 = Ψ·Ψ * = |A| 2 .
И напоследок получим соотношение между импульсом p и энергией E свободной частицы. Вспоминая выражение для длины волны де Бройля, для волнового числа k получим

Возведя это выражение в квадрат и приравняв к равенству для k 2 (3), получим
что совпадает с классическим соотношением.
Тождественность частиц. Бозоны и фермионы. Принцип Паули.
Проделаем опыт по изучению углового распределения упруго рассеянных α-частиц на ядрах углерода 12 C: α + 12 C → α + 12 C. 
Но может быть (рисунок 2б) α-частица рассеялась на угол π — θ и попадает в детектор 2. Этот процесс описывается функцией Ψ(π — θ). Детекторы 1 и 2 включены в схему совпадений, и событие считается зарегистрированным, когда в каждый детектор попадет по частице.
Можно ли сделать детектор, различающий α-частицы и ядра углерода? Отвечаем «да», и случаи 1а и 1б различны. Измеряемая величина — доля частиц, рассеянных на данный угол. В случае а) она пропорциональна |Ψ(θ)| 2 , а в случае б) — |Ψ(π — θ)| 2 . А если детектор не различает частицы (например, счетчик Гейгера), тогда вероятность опыта пропорциональна
Состояния в принципе различны и складываются вероятности.
А при рассеянии α-частиц на ядрах гелия: α + 4 He → α + 4 He (α-частица — это и есть ядро гелия!)? Тут взаимодействуют тождественные частицы, и экспериментальные результаты не согласуются с формулой (5). Полная неразличимость частиц приводит к интерференции рассеянных волн. В этом случае складываются амплитуды
Если подсчитать по этим формулам вероятности для угла θ = π/2, то вероятности 2|Ψ(π/2)| 2 и |2·Ψ(π/2)| 2 = 4·|·Ψ(π/2)| 2 отличаются в два раза. Ошибиться тут нельзя. Опыт согласуется со вторым значением: для неразличимых частиц складываются амплитуды.
А как обстоит дело с электронами? Электроны в отличие от α-частиц имеют спин (собственный момент количества движения), который может иметь два направления. Если спины взаимодействующих электронов направлены одинаково, то это тождественные частицы, но ни (5), ни (6) неверно. Для них складываются амплитуды в противофазе:
Если спины электронов имеют противоположные направления, детектором можно определить, какой электрон попал в детектор, и складываются вероятности (5).
Приходим к выводу: тождественность микрочастиц существенна при описании взаимодействия этих частиц.
Электроны тождественны, и перестановка двух любых экспериментально обнаружена быть не может: возможны переходы, ведущие к неразличимым экспериментально состояниям.
| макрофизика | физика микрочастиц |
|---|---|
| можно пронумеровать частицы, наблюдать за движением определенной | понятие траектории не имеет смысла, теряет смысл и различие частиц. Обозначим волновую функцию, описывающую состояние двух частиц, через Ψ(x1,x2). Здесь x1 — координата первой частицы, x2 — второй. Подействуем на эту функцию оператором перестановки двух частиц местами Но начальное и конечное состояния ввиду тождественности частиц неразличимы, и поэтому волновые функции могут отличаться только постоянным сомножителем. Подействуем этим оператором еще раз и вернемся к исходной волновой функции Получаем a = ± 1. Волновые функции либо меняют знак при перестановке частиц либо нет Спины фермионов полуцелые: 1/2ħ, 3/2ħ. Для фермионов действует принцип Паули: в одном и том же квантовом состоянии не может быть одновременно более одного фермиона, например, электрона. Это утверждение впервые было сформулировано Вольфгангом Паули в 1925 г. Полное обобщённое доказательство этого принципа было им сделано в 1940 г. в рамках квантовой теории поля. Определенное квантовое состояние задается набором квантовых чисел. Например, для атома водорода это четыре числа. |
В 1945г. Вольфгангу Паули присуждена Нобелевская премия:
W OLFGANG P AULI for the discovery of the Exclusion Principle, also called the Pauli Principle.
(за открытие принципа запрета, названного принципом Паули)
Вычисление средних значений
Если известна волновая функция Ψ(x), то можно вычислить значение физических величин, характеризующих данную задачу. Как упоминалось, |Ψ(x)| 2 dx — дает долю частиц, находящихся между x и x + dx. Тогда среднее значение x
Аналогично надо поступить и любых функций координаты x. Например, среднее значение потенциальной энергии U(x) равно
По-другому вычисляется средняя кинетическая энергия, которая зависит не от координаты x, а от импульса. Приведем формулу
Можно проверить последнее выражение для частного случая n = 1 в прямоугольной бесконечно глубокой потенциальной яме
что совпадает со значением полной энергии E в основном состоянии, т.к. потенциальная энергия U полагалась равной нулю.
Излучение и поглощение энергии
Чтобы выяснить, излучает ли система, содержащая заряженную частицу, надо вычислить среднее значение координаты. Если среднее значение x колеблется с частотой ν, то согласно законам электродинамики надо ожидать испускания или поглощения излучения такой частоты.
Используем волновую функцию частицы в состоянии с квантовым числом n и энергией En —
Оказывается, если частица находится в определенном энергетическом состоянии, среднее значение x не зависит от времени, и излучения нет. В 1913 году Нильс Бор для объяснения закономерности линейчатого спектра атома водорода постулировал, что атомная система может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует определенная энергия En. В стационарных состояниях атом не излучает. Этот постулат находился в явном противоречии с классической механикой. 
Теперь рассмотрим систему, в которой есть два состояния с квантовыми числами n, m и соответствующими им энергиями En и Em (рис.3). Принцип суперпозиции в квантовой механике заключается в следующем: если квантовая система может находиться в состояниях, описываемых волновыми функциями Ψn и Ψm, то она может находиться и в состоянии, описываемом волновой функцией
где a и b — произвольные коэффициенты. Наблюдая испускание излучения при возвращении в основное состояние n, можно заключить, что система была в состоянии m (т.е. a = 0, b = 1) в какой-то момент времени. Найдем среднее значение x для функции (8).
В подынтегральном выражении слагаемые с произведениями Ψ * n·Ψn и Ψ * m·Ψm приводят, как мы видели, к стационарным значениям x и не вызывают излучение или поглощение. Поэтому нас будут интересовать перекрестные произведения
Получили, что среднее положение частицы представляет собой периодическую функцию времени, умноженную на некоторое число (определенный интеграл по x). Поэтому получаются колебания заряда, и, следовательно, излучение с частотой
Таким образом, квантовая механика объясняет существование линейчатых спектров и обосновывает вторую гениальную догадку Н.Бора: испускание или поглощение фотонов происходит только с частотами, удовлетворяющими равенству hν = Em — En.
Теперь заметим, что колебаний заряда не будет, если интеграл В (9) равен нулю
Когда это бывает? В лекции о квантовом гармоническом осцилляторе выписаны волновые функции основного и первых двух возбужденных состояний. Для перехода m = 1 → n = 0 этот интеграл (опуская постоянные коэффициенты)
т.к. под интегралом четная функция. Аналогично для перехода m = 2 → n = 1
функция под интегралом четная и интеграл нулю не равен. Переходы m = 1 → n = 0 и m = 2 → n = 1 разрешены и сопровождаются излучением кванта.
Теперь проанализируем переход m = 2 → n = 0.
т.к. под интегралом нечетная функция. Такой переход запрещен. Детальный анализ волновых функций гармонического осциллятора показывает, что возможны только переходы, при которых квантовое число обязательно меняется на единицу Δn = ±1. Это так называемое правило отбора. Для водородоподобных атомов правила отбора будут свои.
Квантовая механика объясняет основные характеристики испускания и поглощения света.
Если возникли какие-либо вопросы, напишите мне.
4.5. Уравнение Шредингера для простейших систем
Свободная частица, движущаяся вдоль оси х
Потенциальная энергия равна нулю: 
Введем волновой вектор 
и перепишем уравнение в виде
Существуют, как известно, два линейно независимых решения уравнения (4.22), так что общее решение есть суперпозиция двух волн — или стоячих:
или бегущих:
(первый член — волна бежит направо, второй — налево; постоянные 




При решении большинства задач квантовой механики следует обратить внимание на то, что волновая функция всегда должна быть непрерывной — вероятность пребывания частицы не может меняться скачком от точки к точке. Кроме того, если потенциальная энергия непрерывна или имеет скачки, но только первого рода (конечные скачки) и не имеет бесконечных скачков (скачков второго рода), то из уравнения Шредингера следует, что и первая производная волновой функции также непрерывна.
Частица в бесконечно глубокой потенциальной яме
Потенциальная энергия в этой задаче имеет вид
Такая система соответствует частице, движущейся вдоль прямой линии и отскакивающей от абсолютно отражающих препятствий в точках 






Общее решение имеет вид
Используем сначала первое граничное условие
Мы получили, что решение уравнения Шредингера должно иметь вид
Если продолжить нашу аналогию, то можно сказать, что на струне, закрепленной в одной точке, бегущих волн не бывает: отражение от неподвижной точки обязательно порождает стоячую волну. Однако на длину волны никаких ограничений не накладывается.
Теперь наложим второе из граничных условий:
Здесь есть два типа решений. При 
что означает отсутствие частицы в яме (вероятность найти ее всюду равна нулю). Поэтому нас интересует второе – нетривиальное – решение, когда
Это возможно лишь при некоторых значениях волнового вектора:
Так как энергия частицы связана с волновым вектором, то
Мы получили квантование энергии, то есть наша «струна», закрепленная с обеих сторон, зазвучала, так как появились выделенные частоты.
Подставляя найденные разрешенные значения волнового вектора в выражение для волновой функции, получаем ее в виде
Смысл квантового числа: оно на единицу больше числа нулей волновой функции. Значение постоянной
определяется из условия нормировки.
Рис. 4.8. Уровни энергии, волновые функции и распределение плотности вероятностей по координате x
Отметим, что значения 



Откуда же берется дискретность уровней энергии, характерная и для атома? Сравним со свободной частицей: уравнения те же, но с иными граничными условиями! Здесь возможны две постановки задачи. В первом случае исследуется состояние, которому в классической механике соответствовало бы инфинитное движение (задача рассеяния). Обычно в таких случаях решения возможны при любых значениях энергии (как говорят, спектр непрерывен). Во втором случае исследуется состояние, которому в классике соответствует финитное движение в ограниченной области пространства (задача на связанные состояния). Требование конечности волновой функции во всем пространстве ведет к квантованию энергии. Подчеркнем: в этом случае стационарное уравнение имеет физически приемлемые решения не всегда, а лишь при некоторых значениях энергии 
Пример. Определим разность соседних уровней энергии 



Используя выражение (4.24) для уровней энергии частицы в потенциальной яме, находим разность энергий соседних уровней
при больших значениях 
Приравнивая 
Уже само по себе это число говорит о том, что в области крайне высоких возбуждений работают классические формулы. Разность энергий соседних уровней получается, подстановкой в формулу для 
В электрон-вольтах те же характеристики имеют значения
Относительная разность энергий соседних уровней ничтожно мала:
и потому в классическом пределе квантовой дискретностью пренебрегают.
Частица в трехмерной потенциальной яме
Это обобщение предыдущей задачи. Частица может двигаться в кубическом объеме с длиной ребра 
Такая волновая функция соответствует очевидному факту, что движения вдоль трех осей не зависят друг от друга, и каждое описывается прежними одномерными волновыми функциями. Энергия, как легко догадаться, будет равна сумме энергий движения по осям x, y, z:
Рис. 4.9. Трёхмерная потенциальная яма
Состояние системы теперь определяется тремя квантовыми числами 





и ей соответствует одна волновая функция 
Но такую энергию имеют теперь три состояния с волновыми функциями 





и вырождение могло бы иметь место лишь при определенных соотношениях между длиной, шириной и высотой потенциального ящика.
Одномерный осциллятор
В классической физике пружинный маятник (одномерный осциллятор) представляет собой точечное тело массой m, прикрепленное к пружине и колеблющееся с круговой частотой 
так что уравнение Шредингера записывается в виде
Отсюда можно найти решение для волновой функции основного состояния
Подставляя это выражение в уравнение Шредингера, легко убедиться, что энергия основного состояния равна
Мы не выписываем волновые функции возбужденных состояний осциллятора, но выражение для разрешенных значений энергии имеет вид ( 
Здесь воспроизводится формула Планка и нулевые колебания

полученные ранее из соотношения неопределенностей (см. разд. 3.3).
Рис. 4.10. Уровни энергии и распределения плотности вероятностей по координате x для разных значений колебательного квантового числа. График потенциальной энергии осциллятора показан синей линией
Рис. 4.11. Распределения вероятностей для классического (пунктир) и квантового (сплошная линия) осцилляторов.
a) n = 1; б) большие значения n
Трехмерный осциллятор
Эта задача является обобщением предыдущей. Как и для трехмерной потенциальной ямы с бесконечно высокими стенками, волновая функция представляется в виде произведения волновых функций одномерных осцилляторов, колеблющихся независимо вдоль осей 


а уровни энергии трехмерного осциллятора описываются формулой
В отличие от одномерного осциллятора состояние определяется значениями трех квантовых чисел 


http://teachmen.csu.ru/work/lectureWaveFunction/index.html
http://online.mephi.ru/courses/physics/atomic_physics/data/course/4/4.5.html
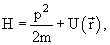
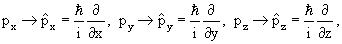
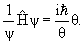
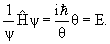
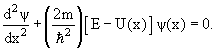
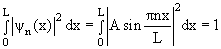
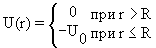
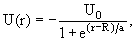







 — оператор Лапласа;
— оператор Лапласа;


































































