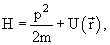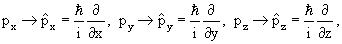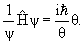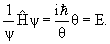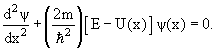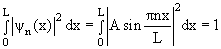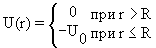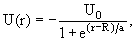Расставляя все точки над «пси»
При планировании нескольких статей так или иначе связанных с квантовой механикой было решено вынести обсуждение ряда технических вопросов, философских споров и досужих мифов в отдельную статью. Речь пойдет о самом сложном и интересном инструменте человеческого интеллекта — квантовой теории.
Я вовсе не физик, но знаю, что к чему.
Попай-моряк
Большая часть нашей коллективной деятельности регулируется другими людьми. Мы получаем от них набор условных обозначений и правила их использования. Владение таким инструментом позволяет нам принимать сообщения и отвечать так, чтоб максимально точно передать результат работы своей нейронной сети. Человеческие правила коллективной деятельности определяют эволюцию нашей культуры.
Напротив, природные системы, от атомов до галактик, развиваются независимо от человеческих правил. Мы не можем изменять физические законы. Мы можем только попытаться понять их. Сама природа судит посредством экспериментов, насколько правдоподобно то или иное объяснение некоторых природных явлений. Тем не менее, в передовых исследованиях, где неизвестное только начинает обретать форму, новое знание достаточно неустойчиво.
Для должного обоснования модели исследователь обязан иметь обширный фундамент. По аналогии с высказыванием «ты — то что ты ешь» справедливо то, что мы оперируем при мышлении лишь знаниями поступившими извне (разумеется с учетом предустановок обусловленных на начальных этапах формирования мозга). Тут уже приходится полагаться помимо собственного чувственного опыта на утверждения окружающих. И не абы кого, а авторитетов.
Для того, чтобы быстро восполнить какой-либо пробел, достаточно вбить в поисковик ключевую фразу, а ля «двухщелевой эксперимент» и пробежаться глазами по предложенным источникам. И пожалуйста, у вас есть знание — быстро, дешево, наглядно! Теперь вы знаете ответ на вопрос и можете даже написать свою статью, чтоб учить окружающих. И она будет иметь шанс выпасть в поисковой выдаче. Вот только почему-то многие не обращают внимание на то, кто был автором ответов. Ютюбовское видео — блогер, бросивший учебу, но популярный из-за смазливой мордашки и умения вставлять мультики в ролик; запись из блога — школьница подросток увлекающаяся астральными путешествиями; статья из научпоп журнала — журналистка, чья специальность не подразумевала никаких технических дисциплин.
Конечно, из любого правила есть исключения, и приходится просматривать большую часть работ автора, чтоб сделать о нем выводы. Может по образованию она и журналистка, но на досуге листает твёрдую литературу. Однако, по вопросам физических моделей я пойду к знакомому доктору физико-математических наук, за объяснением когнитивных процессов полезу в книги специалиста по нейроанатомии, а рецепт наивкуснейших печений спрошу у сестры.
Нам приходится полагаться на мнения специалистов для экономии времени и сил. Если проверять все утверждения и успешные теории самому, то человеческой жизни не хватит, чтоб догнать современный уровень развития общества. От того вера учителям становится необходимой. При этом нужно всегда держать в уме, что они такие же люди и не застрахованы от ошибок, пороков и профдеформации. И будучи мастером своего дела человек будет полнейшим профаном в других аспектах. Даже в пределах одной области познания, мнения у именитых специалистов могут отличаться весьма и весьма. Скажем, Р. Пенроуз будет больше внимание уделять математике, везде и всюду вспоминать Гёделя, а сложную проблему разума спихивать на квантовые явления. Л. Сет — приверженец инженерного подхода, основной упор делает на теорию информации и детерминизм. С. Ааронсон как истинный программист больше внимания уделяет соотношению сложностей вычислений и квантовой информатике.
Физики экспериментаторы предрасположены к позитивизму и материализму. Математики (чаще подверженные комплексу величия) склонны к идеализму, антропоцентризму, а то и солипсизму. Биологи и медики менее религиозны и антропоцентричны чем первые и вторые. А химики… Хм, нужно побольше разузнать про мировосприятие химиков.
В общем, чтобы осмыслять окружающий мир приходится верить тем, кто убивал время на его понимание. А чтобы понять самому, придется поработать ручками и головой.
Где взять понимание
Но если квантовая механика — это не физика в обычном смысле, если она не занимается ни веществом, ни энергией, ни волнами, ни частицами, то чем же она занимается? С моей точки зрения, она занимается информацией, вероятностями, наблюдаемыми величинами и тем, как они соотносятся друг с другом.
Скотт Ааронсон
В нашу эпоху доступной информации важно умение отделять зерно от плевел. Чтобы оперировать определенными образами, нужно рассмотреть проблему с разных ракурсов ознакомившись с точками зрения нескольких авторов. Еще нужно много практики. Квантовая теория это в первую очередь инструмент, а не философское течение, где каждый волен озвучить свое мнение. Для использования этого сложного инструмента нужны инструкции и учителя.
Гуго Штейнгауз как-то сказал: «математик сделает это лучше». Под «это» подразумевается всё. Оно и понятно, ведь занятие точными науками есть многогранная тренировка мышления и привнесение в ум дисциплинированности. Так что, без должных навыков из линейной алгебры, дифференциального исчисления и математической логики с теорией алгоритмов путь в теоретическую физику закрыт. Все остальное самообман и иллюзия понимания — вы просто не будете восприимчивым к грамотным объяснениям, так как мышление не будет генерировать образов, которые пытается донести собеседник или автор касательно данной темы.
Только разобравшись со вспомогательными инструментами из матана и с основами классической физики (механика, электродинамика, оптика, статы) можно приступать к квантам. Тут не сдержусь порекомендовать литературу «которая навсегда перевернет ваше сознание»
- Иванов М.Г. Как понимать квантовую механику 2015 (Название говорит само за себя. В книге можно найти теоретический минимум и выжимку из философских рассуждений)
- Тихонов Д. Теоретическая химия: внутри чёрного ящика (Неформальная методичка. Кого-то может отпугнуть лукморовский стиль изложения, кого-то, наоборот, привлечь. Наиболее ценна из-за ликбеза по основным материалам и кропотливых выкладок, а также раскрытия важных аспектов химической физики)
- Блохинцев Д.И. Принципиальные вопросы квантовой механики 1966 (Большой упор на философию и методологию. Лично мне понравился вход в тему со стороны статистической физики)
- Бом Д. Квантовая теория 1952 (Потряснейший учебник от товарища Бома, изданный им до перехода на темную сторону. Вход в тему со стороны электродинамики и постоянные поиски смысла. Особенно интересно идет с нападками редактора русского издания Вонсовского)
- Дирак П. Принципы квантовой механики 1958 (Одна из тех редких книг, которую хочется иметь в бумажном виде, чтобы читать по вечерам у камина)
- Балашов В.В. Курс квантовой механики 2001 (Хороша задачками и некоторыми аспектами не раскрытыми в других учебниках)
- Фейнман Р. Статистическая механика курс лекций (Много крутых тем, но требует основательный бэкграунд по матану)
- Флюгге З. Задачи по квантовой механике 1974 (Ну а вы как хотели? Полистать оглавления и все? Еще надо задачки решать!)
- Хренников А.Ю. Введение в квантовую теорию информации 2008 (Это для встряски)
- Jon Magne Leinaas Modern Quantum Mechanics 2016 (Современно, без воды, я б сказал хороший скелет)
- David J. Griffiths Introduction to Quantum Mechanics 2004 (А здесь уже с мясцом и философией)
- Ну и в прошлой публикации есть список литературы по квантовым вычислениям, там как правило присутствует ликбез по теме
Если вы не проявляли усилий для основательного освоения материала, то будьте честны хотя бы с собой — вы сторонний наблюдатель и нефига в квантах не смыслите. Не встревайте в споры, не выдвигайте теории и уж тем более не учите окружающих. Ну да, это наболевшее. Ладно здесь на хабре и еще много на каких технических форумах и тематических группах проскакивает дичь, порожденная необразованностью автора, но когда два профессора подряд на лекциях по философии упраздняли квантовую механику и теорию относительности, тут уж мне многое пришлось переосмыслить.
Однако же, на время отвлечемся от пространных разговоров и поработаем руками.
Уравнение Шредингера
Таким образом, основные физические законы, необходимые для математической теории значительной части физики и всей химии, полностью известны, и трудность заключается лишь в том, что точное применение этих законов приводит к уравнениям, которые слишком сложны, чтобы быть разрешимыми. Поэтому становится желательным разработать приближенные практические методы применения квантовой механики, которые могут привести к объяснению основных особенностей сложных атомных систем без слишком больших вычислений.
П. Дирак
В наиболее общем случае эволюцию (переход между состояниями) абстрактной системы можно описать взаимно-однозначными афинными преобразованиями фазового пространства: . В квантовом случае это будет перевод операторов плотности. Свойство аффинности имеет прямой статистический смысл: оно означает сохранение «весов» в смесях состояний.
Введя унитарный оператор U, мы имеем — афинное взаимно-однозначное отображение множества квантовых состояний S на себя, то есть, обратимую эволюцию. При обратимой эволюции чистые состояния переходят в чистые, при этом вектор исходного чистого состояния
преобразуется в
.
Для непрерывной однопараметрической группы унитарных операторов удовлетворяющей условиям:
(однородность по времени)
- непрерывность функции
работает теорема Стоуна
где H — эрмитов оператор, а параметр t обычно играет роль времени. И вот, для векторов чистых состояний можно получить уравнение Шредингера
> <\partial t>= \hat
Из терминологии классической механики: — гамильтониан, оператор полной энергии системы, то есть, сумма кинетической энергии
и энергии системы в поле некоего потенциала.
Тем кто полюбил линейную алгебру занимаясь компьютерной графикой (привет пользователям OpenGL), уравнение как бы намекает, что эволюция чистой квантовой системы это повороты вектора состояния путем умножения на матрицу-гамильтониан.
Формально, уравнение Шредингера ни откуда не выводится, будучи в нерелятивистской квантовой механике наиболее общим. Оно постулируется как обобщение экспериментов. Хотя, в книге Бома можно посмотреть довольно органичный способ его получения на основе выражения волны для свободной частицы.
Практически вся волновая теория заключена в волновом уравнении, если мы знаем, как интерпретировать волновую функцию. Уравнение Шредингера является математическим выражением корпускулярно-волнового дуализма микрочастиц. В предельном случае, когда длины волн де Бройля значительно меньше размеров рассматриваемого движения, уравнение Шредингера позволяет описывать движение частиц по законам классической механики.
С математической точки зрения — это дифференциальное уравнение в частных производных, которое имеет множество решений. В каждой конкретной задаче из этого множества следует выбрать одно решение, отвечающее условиям задачи.
С физической точки зрения нужно отметить, что согласно уравнению Шредингера волновая функция изменяется детерминировано, то есть совершенно однозначно. В этом смысле квантовая механика напоминает классическую, в которой движение системы заранее предопределено начальными условиями. Однако сама волновая функция имеет вероятностный смысл.
Наконец, необходимо отметить важную особенность уравнения Шредингера: оно линейно. Волновая функция и ее производные входят в него в первой степени и для волновых функций справедлив принцип суперпозиции. Он позволяет сложные модели разбивать на подзадачи.
Факторизуя волновую функцию на временную и на пространственные компоненты получаем одномерное стационарное Уравнение Шредингера
Это ни что иное, как задача на собственные значения оператора Гамильтона. Энергия – одна из наблюдаемых, следовательно, это уравнение на допустимые наблюдаемые значения энергии и на соответствующие им состояния системы. Получим общее решение для нулевого потенциала:
Теперь знай себе, подставляй граничные и начальные условия в зависимости от задачи. Так можно получить, например, аналитическое выражение для свободной частицы в потенциальной яме, дающее вероятности локализации в некотором пространстве
К этой модели сводится, например, движение -электрона в цепи полиена
.
Если же учитывать внешний потенциал (а он разнится в зависимости от среды) то волновую функцию в некой слоистой структуре можно представить в виде:
Используя граничные условия и довольно красивый метод матриц переноса получаем спектр и собственные функции для последовательности произвольных постоянных потенциалов
Этой же методой выуживают значения энергии резонансных переходов электронов в слоисто-неоднородных средах.
Чтобы не перегружать страницу формулами и кодом укажем ссылки на исходники и pdf-аналоги: раз два
Численные методы
Очень хорошо когда задача сводится к известной модели. Но не всегда удается получить аналитическое решение. Поэтому в квантмехе найдется работа не только чистым теоретикам, но и грязным числодробителям. Уравнение Шредингера вполне себе типичная дифура, для которых разработана уйма методов. Поиграем с одним из них.
Разностная аппроксимация по времени уравнения Шредингера с использованием метода Кранка-Николсона имеет вид:
Которую можно переписать в виде:
В одномерном случае конечно-разностная схема по координате расписывается как:
Это соответствует построению для гамильтониана разреженной матрицы. Например, для гамильтониан и волновая функция становятся:
Вот и все, теперь достаточно задать начальный волновой пакет, вид потенциального барьера, взять побольше шагов по времени и координате и пожалуйста — анимации квантовых явлений рассчитанные силами вашего пк:
Еще может быть интересна имплементация расщепления шага Фурье и решение несколькими методами нелинейного уравнения Шредингера находящего применение в физике плазмы, в частности при моделировании нелинейных быстрых магнитозвуковых волн в корональных магнитных трубках.
Но разумеется не все так радужно. Чем больше объектов в изучаемой системе, тем сложнее будет модель. Например, для молекулы воды в оператор Гамильтона будут входить импульсы трех ядер (два ядра водорода и одно кислорода) и 10 электронов, а также потенциалы кулоновского взаимодействия всех пар частиц:
И какой же ужас нас ждет когда мы захотим промоделировать элементарную химическую реакцию веществ в этой воде растворенных — каждый электронный переход происходит с оглядкой на наведенное поле, в свою очередь влияя на окружающие дипольные моменты молекул воды. А если же вам вздумается моделировать геометрию органических молекул.
И тут на помощь приходят семиэмпирические и квазиклассические методы, а также уйма эвристик, упрощений и хитрых солверов.

Метан собранный усилиями Gamess

Структура 5XER обсчитанная с учетом окружения
Такого жанра расчеты часто проводятся при проектировании микроэлектроники, в материаловедении, дефектоскопии, медицине и общей химии, то есть в плане практики детище умов двадцатого века находит все больше применений.
Если кто-то проталкивает мысль, что волновая механика бесполезна или ничего не объясняет, то значит для него это слишком сложно. Все еще надеюсь, что экзамен по философии пройдет в устной форме, уж тогда-то можно будет отыграться за всю ту боль, что эти гуманитарии причиняли на лекциях 🙂
Однако, перейдем к самым спорным мысленным и реальным экспериментам.
Эксперимент Штерна—Герлаха
Хотя наибольшую популярность у общественности снискал опыт Юнга с двухщелевым интерферометром, зарекомендовавшийся как самый контринтуитивный подарок микромира, лично мне больше нравится в этом плане эксперимент Штерна—Герлаха 1922 года
Из печи выпускаются быстрые атомы серебра, которые проходя через сильное магнитное поле образуют на экране зеркальное напыление. Атомы металлов имеют сложную структуру, поэтому для пущей наглядности можно брать водород. Из-за движения электрона в окрестности атома должен возникать магнитный момент, и напрашивается предположение, что в магнитном поле атом ведет себя как маленький магнитик. Имея произвольную начальную ориентацию наши магнитики, испытывая отклонение при прохождении внешнего поля, должны распределиться на экране более-менее равномерно. Не тут-то было! На экране будут кучки, которые можно посчитать по пальцам, а значит магнитные свойства квантуются. Пришлось вводить спин — собственный момент — дающий, наряду с орбитальным, вклад в полный момент атома.
И вот измеряя, скажем, Z компоненту мы получаем на выходе из установки два пучка. Видимо электроны делятся на два сорта: на мальчиков и девочек. Теперь затащим в лабораторию рояль и минибар еще одну установку и опрокинем ее набок супротив первой, так чтобы на вход второй подавался один из потоков струящихся из первой.
И на выходе получаем опять два пучка. То есть в новом ортогональном направлении тоже есть свой вклад. Ну ладно, девочки бывают разные… Занесем пилоны и лаборанток еще установку и сориентируем вертикально пристроив к первым двум
И опять на выходе два пучка! Это пошатывает убежденность, что спин является объективной характеристикой, которая может существовать до взаимодействия с экспериментальной установкой. Надеюсь, вы достаточно заинтригованы. Подробные детали и обсуждение результатов каскадного эксперимента Штерна-Герлаха в рамках кубитной модели читайте в книге Квантовые вычисления и квантовая информация М. Нильсен, И. Чанг. Возможно, мы потом вернемся к этому опыту в рамках различных интерпретаций.
(todo: поискать эксперименты с различным временем пребывания в МП)
Тот самый кот
Я напомню, что во время одной прогулки Эйнштейн неожиданно остановился, повернулся ко мне и спросил, действительно ли я верю, что Луна существует только тогда, когда я смотрю на нее. Оставшаяся часть прогулки была посвящена обсуждению того, что физик должен понимать под словом «существовать».
А. Пэ
Часто кота Шрёдингера используют для нагнетания мистицизма. Этот мысленный эксперимент раздувают до парадокса, им пытаются объяснять сложность и противоречивость квантовой механики или даже утверждают, что ее суть передается этим мемом. В зависимости от уровня абстрактного и критического мышления люди застревают на разных этапах: кто-то начинает спор на счет пола животного, кто-то плачет, что кису жалко, некоторые начинают прикапываться к деталям установки, многие спорят о роли наблюдателя.
С наблюдением вообще отдельная история. В экспериментах под процессом наблюдения понимается взаимодействие исследуемой системы с измерительным прибором. Наблюдателем можно считать и газоразрядный счетчик Гейгера и фотодетектор с мультиметром, а не только человека слушающего треск и видящего показания на дисплее. Для квантовых систем важна их чистота достигаемая изоляцией от внешних воздействий. Именно тогда на достаточно больших временах эволюцию можно описывать уравнением Шрёдингера. Если вы, скажем, поставили детектор возле одной из щелей в опыте Юнга, то получается вы привнесли в систему наблюдателя — многочастичную хреновину ограничивающую пространственные степени свободы исследуемых объектов. Подробней этот вопрос раскрыт в книге Бома в 6 части. Там он очень даже неплохо для 50х годов прошлого века проследил процесс измерения вплоть до мозга экспериментатора.
Опять же, нюансы это вопрос интерпретации, но с точки зрения матаппарата всё довольно согласовано и пригодно для практических применений. К слову, если уж совсем не хочется работать с литературой и привычней разжеванный видеоконцентрат, то можно посмотреть хотя бы на материалы по теме от ребят из физтеха. При просмотре вспомнил про подобное объяснение для трехщелевого эксперимента (да, это тот, где выходят отрицательные вероятности) в лекциях по матрицам плотности от Никитина Н.В.
Вернемся к котикам. Объяснения этого эксперимента желательно смотреть не по бложикам и видосикам, а в крепкой литературе. Возможно вы заметите, что во многих монографиях мысленные эксперименты и философия поднимаются в конце, уже после изложения необходимого формализма. Тогда уже приходит понимание, что и кот и ЭПР возникли во времена, когда терминология только формировалась и многим хотелось таким образом выразить свое недовольство какими-либо нюансами. В частности Шредингер с котом хотели заострить внимание на грани между микро- и макро-.
Источником проблемы является неопределенность, связанная со статистической интерпретацией волновой функции, которая однозначно не определяет результат измерения. Все, что она дает, — это статистическое распределение возможных результатов.
В связи с этим возникает глубокий вопрос: действительно ли физическая система «имела» рассматриваемый атрибут до измерения (так называемая реалистическая точка зрения), или же сам акт измерения «создал» это свойство, ограниченное лишь амплитудой вероятности (ортодоксальная позиция). Или же мы можем списав на метафизику сказать, что никакого смысла в этих спорах нет (агностика ответ).
Согласно реализму, квантовая механика — это неполная теория, ибо даже если вы знаете все, что квантовая механика может рассказать вам о системе, вы все равно не можете определить все ее особенности. Очевидно, существует и другая информация, внешняя по отношению к квантовой механике, которая необходима для полного описания физической реальности. Тут уже появляются теории со скрытыми переменными, парочку из которых вместе с неравенствами Белла рассмотрим позже.
Ортодоксальная позиция поднимает еще более тревожные проблемы, ибо если акт измерения заставляет систему «занять позицию», помогая создать атрибут, которого раньше не было, то в процессе измерения есть что-то очень своеобразное. Более того, чтобы объяснить тот факт, что немедленно повторенное измерение дает тот же самый результат, мы вынуждены предположить, что акт измерения разрушает волновую функцию таким образом, который в лучшем случае трудно согласовать с нормальной эволюцией, предписанной уравнением Шредингера. В свете этого неудивительно, что многие поколения физиков отступили на позиции агностиков и советовали своим ученикам не тратить время на размышления о концептуальных основах теории.
В период становления копенгагенской интерпретации, которая была сколочена на скорую руку, многие не соглашались с постулированным существованием объективной случайности и с нелокальностью коллапса волновой функции. В последующих трактовках ортодоксальной интерпретации сошлись на нефизичности коллапса, а для решения многих проблем ввели декогеренцию — разрушение самосогласованного состояния при запутывании квантовых объектов. В частности, проблема с котом решилась тем, что механизм приводящий в действие машину смерти производит измерение квантовой системы, непреклонно вынуждая ее принять значение из спектра собственных чисел.
Такое решение, по крайней мере, позволяет избежать отупляющего солипсизма Вигнера и других, которые убеждали себя, что именно вовлеченность человеческого сознания составляет измерение в квантовой механике. Частью проблемы является само слово «измерение» или «наблюдение», которое, безусловно, несет в себе намек на человеческое участие. Гейзенберг предложил слово «событие», которое, возможно, было бы предпочтительнее. Но ничего не поделаешь, термин устоялся и еще долго будет импонировать доморощенным упразднителям мирового заговора и бередить слух вовлеченных в тему.
Касательно ЭПР и неравенств Белла можно будет поговорить уже в рамках интерпретаций. Конечно, чтобы развеять иллюзии и непонимание каждый должен сам пройти через тонны литературы и исписанных тетрадей. Да, довольно субъективно, но я испытал это на своей шкуре, от отторжения того что вдалбливают на лекциях и уверенности, что всем просто пудрят мозги, до получения формул совпадающих с результатами экспериментов.
Будет сложно, но оно стоит того. Чтобы ни говорили про религиозные тексты (кстати, именно Библия убила во мне христианина), о том как они расставляют все на свои места и дают ответы на сокровенные вопросы, они не сравнятся с красотой математики различных формализмов, с хитросплетением связей разделов физики, с объяснительной мощью эволюционной теории и с простотой фундаментальных принципов, порождающих многообразие вселенских масштабов. Познание открывает взору все больше красоты окружающего мира. А разве не в этом состоит смысл жизни?
Уравнение Шрёдингера
Дуальная корпускулярно-волновая природа квантовых частиц описывается дифференциальным уравнением.
Согласно фольклору, столь распространенному среди физиков, случилось это так: в 1926 году физик-теоретик по имени Эрвин Шрёдингер выступал на научном семинаре в Цюрихском университете. Он рассказывал о странных новых идеях, витающих в воздухе, о том, что объекты микромира часто ведут себя скорее как волны, нежели как частицы. Тут слова попросил пожилой преподаватель и сказал: «Шрёдингер, вы что, не видите, что всё это чушь? Или мы тут все не знаем, что волны — они на то и волны, чтобы описываться волновыми уравнениями?» Шрёдингер воспринял это как личную обиду и задался целью разработать волновое уравнение для описания частиц в рамках квантовой механики — и с блеском справился с этой задачей.
Тут необходимо сделать пояснение. В нашем обыденном мире энергия переносится двумя способами: материей при движении с места на место (например, едущим локомотивом или ветром) — в такой передаче энергии участвуют частицы — или волнами (например, радиоволнами, которые передаются мощными передатчиками и ловятся антеннами наших телевизоров). То есть в макромире, где живём мы с вами, все носители энергии строго подразделяются на два типа — корпускулярные (состоящие из материальных частиц) или волновые. При этом любая волна описывается особым типом уравнений — волновыми уравнениями. Все без исключения волны — волны океана, сейсмические волны горных пород, радиоволны из далеких галактик — описываются однотипными волновыми уравнениями. Это пояснение нужно для того, чтобы было понятно, что если мы хотим представить явления субатомного мира в терминах волн распределения вероятности (см. Квантовая механика), эти волны также должны описываться соответствующим волновым уравнением.
Шрёдингер применил к понятию волн вероятности классическое дифференциальное уравнение волновой функции и получил знаменитое уравнение, носящее его имя. Подобно тому как обычное уравнение волновой функции описывает распространение, например, ряби по поверхности воды, уравнение Шрёдингера описывает распространение волны вероятности нахождения частицы в заданной точке пространства. Пики этой волны (точки максимальной вероятности) показывают, в каком месте пространства скорее всего окажется частица. Хотя уравнение Шрёдингера относится к области высшей математики, оно настолько важно для понимания современной физики, что я его все-таки здесь приведу — в самой простой форме (так называемое «одномерное стационарное уравнение Шрёдингера»). Вышеупомянутая волновая функция распределения вероятности, обозначаемая греческой буквой ψ («пси»), является решением следующего дифференциального уравнения (ничего страшного, если оно вам не понятно; главное — примите на веру, что это уравнение свидетельствует о том, что вероятность ведёт себя как волна):
где x — расстояние, h — постоянная Планка, а m, E и U — соответственно масса, полная энергия и потенциальная энергия частицы.
Картина квантовых событий, которую дает нам уравнение Шрёдингера, заключается в том, что электроны и другие элементарные частицы ведут себя подобно волнам на поверхности океана. С течением времени пик волны (соответствующий месту, в котором скорее всего будет находиться электрон) смещается в пространстве в соответствии с описывающим эту волну уравнением. То есть то, что мы традиционно считали частицей, в квантовом мире ведёт себя во многом подобно волне.
Когда Шрёдингер впервые опубликовал свои результаты, в мире теоретической физики разразилась буря в стакане воды. Дело в том, что практически в то же время появилась работа современника Шрёдингера — Вернера Гейзенберга (см. Принцип неопределенности Гейзенберга), в которой автор выдвинул концепцию «матричной механики», где те же задачи квантовой механики решались в другой, более сложной с математической точки зрения матричной форме. Переполох был вызван тем, что ученые попросту испугались, не противоречат ли друг другу два в равной мере убедительных подхода к описанию микромира. Волнения были напрасны. Сам Шрёдингер в том же году доказал полную эквивалентность двух теорий — то есть из волнового уравнения следует матричное, и наоборот; результаты же получаются идентичными. Сегодня используется в основном версия Шрёдингера (иногда его теорию называют «волновой механикой»), так как его уравнение менее громоздкое и его легче преподавать.
Однако представить себе и принять, что нечто вроде электрона ведёт себя как волна, не так-то просто. В повседневной жизни мы сталкиваемся либо с частицей, либо с волной. Мяч — это частица, звук — это волна, и всё тут. В мире квантовой механики всё не так однозначно. На самом деле — и эксперименты это вскоре показали — в квантовом мире сущности отличаются от привычных нам объектов и обладают другими свойствами. Свет, который мы привыкли считать волной, иногда ведёт себя как частица (которая называется фотон), а частицы вроде электрона и протона могут вести себя как волны (см. Принцип дополнительности).
Эту проблему обычно называют двойственной или дуальной корпускулярно-волновой природой квантовых частиц, причем свойственна она, судя по всему, всем объектам субатомного мира (см. Теорема Белла). Мы должны понять, что в микромире наши обыденные интуитивные представления о том, какие формы может принимать материя и как она себя может вести, просто неприменимы. Сам факт, что мы используем волновое уравнение для описания движения того, что привыкли считать частицами, — яркое тому доказательство. Как уже отмечалось во Введении, в этом нет особого противоречия. Ведь у нас нет никаких веских оснований полагать, будто то, что мы наблюдаем в макромире, должно с точностью воспроизводиться на уровне микромира. И тем не менее дуальная природа элементарных частиц остается одним из самых непонятных и тревожащих аспектов квантовой механики для многих людей, и не будет преувеличением сказать, что все беды начались с Эрвина Шрёдингера.
Уравнение шредингера в квантовой физике простыми словами
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
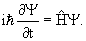 | (4.1) |
где 
в которой 







х → 


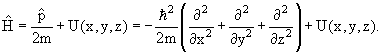 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


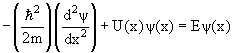
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
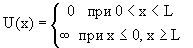 | (4.5) |
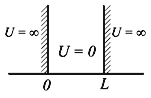
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
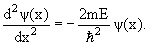 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
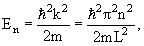 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
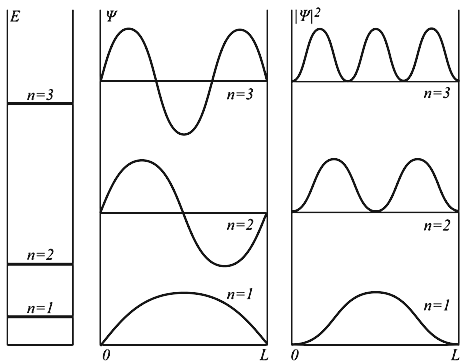
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
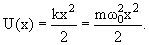 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
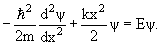 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
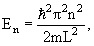

Одномерный гармонический осциллятор:
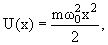
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
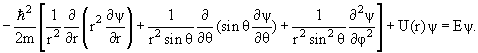 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
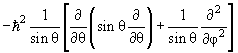 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 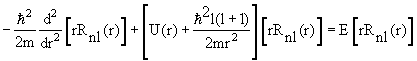 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
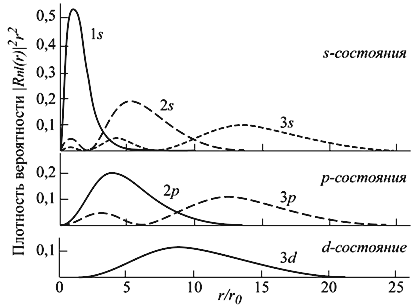
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
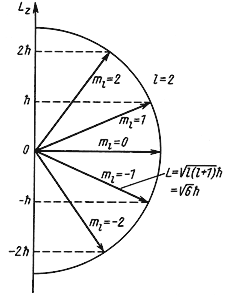
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
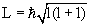 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
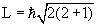
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
http://elementy.ru/trefil/21/Uravnenie_Shryodingera
http://nuclphys.sinp.msu.ru/sem2/sem04.html