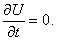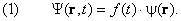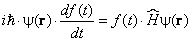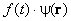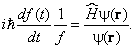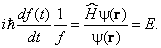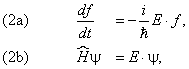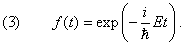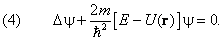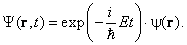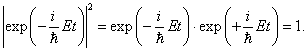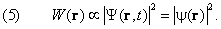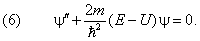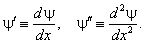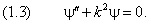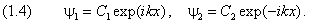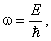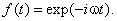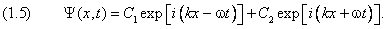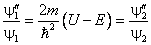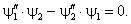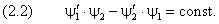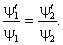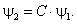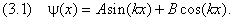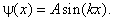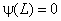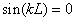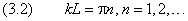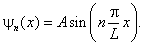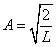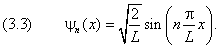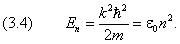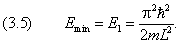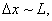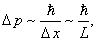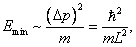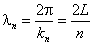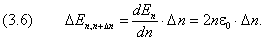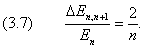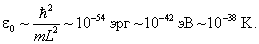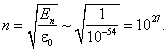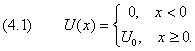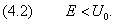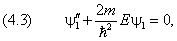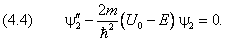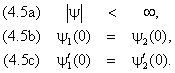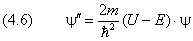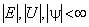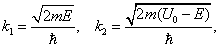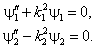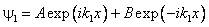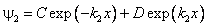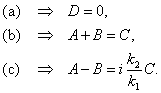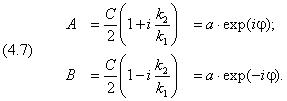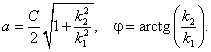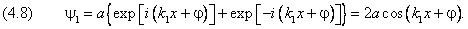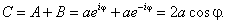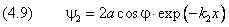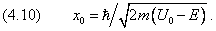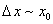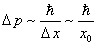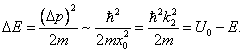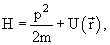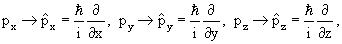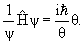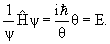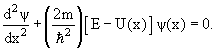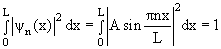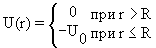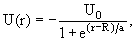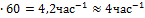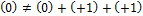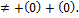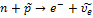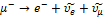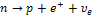Уравнение шредингера в потенциальном ящике
Особое место занимают задачи, в которых потенциальная энергия зависит только координат:
Такие состояния называются стационарными, так как в них сохраняется энергия системы E. Отсутствие явной зависимости гамильтониана от времени позволяет выполнить разделение переменных. Волновую функцию ищем в виде произведения
Множитель f ( t ) отражает волновую природу частиц в квантовой теории. Мы в этом убедимся, когда выведем для него явное выражение. Подставим (1) в уравнение Шредингера (8.1.8):
и разделим обе части равенства на произведение
Левая часть зависит лишь от времени, а правая — только от пространственных координат. Следовательно, они обе равны одной и той же константе:
Легко убедиться, что константа имеет размерность энергии. Таким образом, имеем два уравнения
причём второе показывает, что константа разделения E действительно равна энергии системы. Зависимость волновой функции от времени получаем из (2a):
Итак, временнóй множитель стационарного состояния является осциллирующей функцией. Энергии E соответствует частота 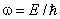
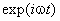
Пространственная часть волновой функции удовлетворяет уравнению (2b), которое с учётом выражения (1.7) восьмой главы для оператора Гамильтона можно переписать как:
Мы получили стационарное уравнение Шредингера. Полная волновая функция имеет вид
Плотность вероятности в стационарном случае не зависит от времени. В самом деле, квадрат модуля временнóго множителя (3) равен единице:
Следовательно, вероятность W найти частицу в той или иной точке пространства (формула (2.1) восьмой главы) определяется исключительно координатной частью волновой функции:
Формула (5) окончательно проясняет смысл функции f ( t ). Последняя описывает волновые свойства стационарного состояния, но никак не влияет на местоположение частицы.
В одномерном случае (4) сводится к обыкновенному дифференциальному уравнению второго порядка
Штрихом для краткости обозначен оператор дифференцирования по единственной пространственной координате x :
В дальнейшем мы рассмотрим несколько задач для простейших одномерных потенциалов.
9.1 Свободная частица
Решим уравнение (6) предполагая отсутствие внешних полей, то есть, при равном нулю потенциале U :
получаем уравнение гармонической функции
Его два линейно независимых решения равны:
Далее, введём частоту
и перепишем временнýю часть волновой функции в виде
Полная волновая функция равна
Таким образом, решением уравнения (1.1) являются две плоские волны, распространяющиеся в противоположные стороны. Мы снова вернулись к связи между свободной частицей и монохроматической волной.
Формула (1.5) иллюстрирует важное свойство микромира. А именно, одному значению энергии может соответствовать несколько различных квантовых состояний. Такие уровни энергии принято называть вырожденными, а число квантовых состояний — степенью вырождения, или статистическим весом. В данном случае статистический вес равен двум, соответственно числу возможных направлений движения волны. Явление вырождения является типичным для квантовой механики.
В случае одномерного движения вырождение определяется именно возможностью частице свободно двигаться в обоих направлениях. Покажем, что если её движение ограничено хотя бы с одной стороны, то вырождение исчезает.
9.2. Одномерное движение, ограниченное с одной стороны.
Поставим вопрос, насколько могут различаться волновые функции y 1 и y 2, являющиеся решением уравнения (6), если они соответствуют одному и тому же уровню энергии E. Предполагается, что частица может неограниченно удаляться только в одном из двух направлений по оси x . Покажем, что при выполнении этого условия обе функции описывают одно и то же квантовое состояние. Поскольку они удовлетворяют уравнению (6), мы можем записать
(2.1)
В последнем равенстве прибавим и вычтем произведение 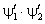
Теперь воспользуемся условием частичной ограниченности движения. В направлении, куда частица не имеет права двигаться неограниченно, обе волновые функции на бесконечности исчезают. Следовательно, константа в правой части (2.1) равна нулю, и справедливо равенство
После повторного интегрирования получим
Согласно пункту «Принцип суперпозиции» раздела 2.1 восьмой главы, волновые функции, различающиеся лишь постоянным множителем, описывают одно и то же состояние.
Итак, вырождение отсутствует, если движение частицы вдоль прямой ограничено хотя бы с одной стороны.
9.3 Частица в потенциальном ящике
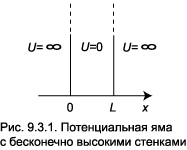
Рассмотрим задачу о прямоугольной потенциальной яме с бесконечно высокими стенками. На рис.9.3.1 ей соответствует потенциал следующего вида: В промежутке 0 x L он равен
нулю и частица там движется свободно, а за пределами этого интервала ( x x > L) потенциал равен бесконечности. В области 0 ≤ x ≤ L уравнение Шредингера сводится к (1.1). В задаче о свободной частице мы получили осциллирующие решения (1.4), которые записали в виде экспоненты с мнимыми показателями ± i kx . Сейчас нам удобнее перейти к эквивалентному представлению, содержащему синус и косинус:
Константы A, B и k найдём из граничных условий и нормировки волновой функции. На стенках волновая функция обращается в нуль, так как в силу бесконечности потенциала частица не может выйти за пределы интервала 0 ≤ x ≤ L. Первое граничное условие даёт
что позволяет уточнить (3.1):
накладывает ограничения на величину волнового числа частицы. В самом деле, из уравнения
Обратим внимание на то, что параметр n не принимает нулевого значения, так как в этом случае волновая функция повсюду равна нулю, что означает отсутствие частицы в ящике. Таким образом, мы получили решение
Константу A найдём из условия нормировки (8.2.7):
для любого n . Итак, нормированная волновая функция n –го состояния равна
Собственному вектору задачи (3.3), согласно (3.2) и (1.2), соответствует собственное значение энергии
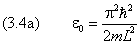
Мы получили дискретный энергетический спектр, иными словами — квантование энергии. Состояние, в котором частица имеет самое низкое из всех возможных значение энергии, принято называть основным. В рассматриваемой задаче основное состояние отвечает значению n = 1. Остальные уровни энергии называют возбуждёнными.
Энергия частицы в потенциальном ящике не может принимать нулевого значения:
Этот факт имеет чисто квантовую природу. Действительно, если мы локализуем частицу на отрезке длиной L:
то, согласно соотношению неопределенностей Гайзенберга , она имеет импульс
а, следовательно, её минимальная энергия составит
что с точностью до численного множителя совпадает с величиной 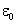
Формулы (3.3) и (3.4) показывают, что волновая функция однозначно определяется значением энергии. Таким образом, в данном случае вырождение не имеет места, в согласии с общим результатом, полученным в предыдущем разделе.
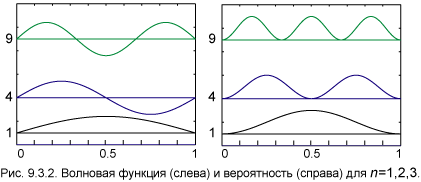
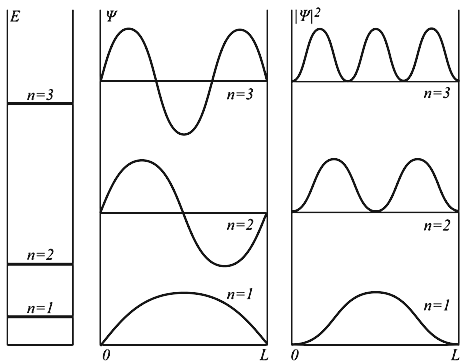
На рис.9.3.2 изображены волновая функция y ( x ) (слева) и вероятность W( x ) (справа) для
трёх первых значений n = 1, 2, 3. По горизонтальной оси отложено отношение x /L. Чёрным цветом обозначено основное состояние, синим — n = 2 и зелёным — n = 3. Прямые линии параллельные оси x (1, 4 и 9) отмечают значение энергии. В тех точках, где волновая функция обращается в нуль, частица никогда не будет обнаружена. Нулям функции W( x ) нет аналогии в классической механике, но им соответствуют узлы стоячих волн в теории колебаний.
Подсчитаем число узлов волновой функции. Функция, описывающая основное состояние частицы, обращается в нуль только на концах интервала, а внутри него она узлов не имеет. В первом возбуждённом состоянии волновая функция имеет ровно один корень внутри отрезка (0, L), во втором — два и так далее. Здесь проявляются общие закономерности одномерного движения.
В математике известна так называемая осцилляционная теорема, справедливая для дискретного спектра энергии. Она связывает друг с другом номер собственного значения и число узлов волновой функции. Перенумеруем собственные значения оператора с помощью числа n , принимающего следующий ряд значений:
Функция ψ n ( x ), соответствующая собственному значению E n , при конечных значениях аргумента обращается в нуль ровно n раз. Если, как в рассматриваемой задаче, частица может находиться только на ограниченном отрезке оси x , то речь идёт о нулях функции ψ n ( x ) внутри этого отрезка. Волновая функция основного состояния ( n = 0 ) узлов не имеет.
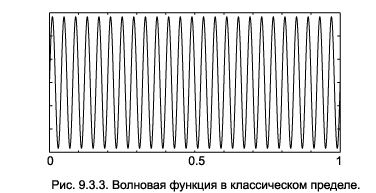
Плотность вероятности, соответствующая очень большим значениям n , быстро осциллирует (рис.9.3.3). В случае прибора с конечной разрешающей способностью в его апертуру попадает много пиков, и мы таких осцилляций не обнаружим. Так квантовая механика переходит в классическую .
Длина волны де Бройля
в классическом пределе n>>1 значительно меньше размеров системы L. Это случай геометрической оптики (классической механики), когда волновыми свойствами частицы можно пренебречь. Квантование энергии при этом тоже становится незаметным. Разность энергий 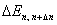
При увеличении квантового числа n энергетическая щель между двумя соседними уровнями ( Δn = 1) растёт медленнее, чем энергия уровней:
Таким образом, сильно возбуждённые состояния в классическом пределе ( 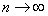
Некоторые примеры
Рассмотрим различные варианты движения частицы, меняя её массу и область локализации.
1. Макроскопическая частица в макроскопических масштабах: m = 1г, L = 1см. Для неё
Такую величину измерить невозможно. Оценим номер уровня при скорости движения V = 1 см/ с . Кинетическая энергия
m V 2 составляет около 1 эрг. Отсюда, согласно (3.4),
Энергетическая щель (3.7) между соседними уровнями составляет
Она также слишком мала, чтобы её можно было обнаружить. Таким образом, макроскопическая частица находится на очень высоком квантовом уровне, а расстояние между соседними уровнями настолько мало, что квантовых свойств мы наблюдать не будем. Поэтому энергетический спектр является практически непрерывным, в соответствии с (3.7).
2. Электрон в макроскопических масштабах длин: m
1 см. Его энергетический спектр почти совпадает с (3.8).
3. Электрон в атоме: L
10 –8 см. В этом случае квант энергии по порядку величины равен
оказывается вполне сравнимым с оценкой энергии основного состояния атома (1.2.5).
Итак, дискретность энергетического спектра заметна только для микроскопических частиц в микроскопических масштабах. Энергия макроскопических частиц на любых масштабах, а также микрочастиц в макроскопических масштабах имеет спектр, практически неотличимый от непрерывного .
9.4 Потенциальный порог
Согласно классической механике, частица, налетая на потенциальный порог, проскакивает его, если её энергия достаточно велика. В противном случае она отражается от барьера.
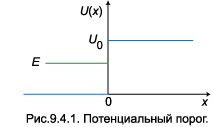
В квантовой механике ситуация сложнее. На рис.9.4.1 график потенциальной энергии U ( x ) изображён синей линией. Функция U ( x ) обращается в нуль в области отрицательных значений аргумента и равна постоянной величине U0 для x ≥ 0:
В точке x = 0 потенциальная энергия терпит разрыв. Энергия налетающей частицы E помечена зелёным цветом. В этом разделе мы будем считать, что энергия частицы меньше потенциального барьера:
В классической механике такое неравенство означает отражение частицы. Переходим к решению уравнения Шредингера. Для отрицательных значений аргумента оно записывается как
а в области x ≥ 0 имеет вид
Решение этих уравнений должно удовлетворять следующим условиям:
Условие (4.5a) означает ограниченность волновой функции. Оно вытекает из того, что вероятность | y | 2 обнаружить частицу в той или иной точке пространства должна быть конечной величиной. Требование непрерывности волновой функции (4.5b) отражает отсутствие процессов рождения и аннигиляции частиц. Непрерывность первой производной является следствием ограниченности потенциала. Для вывода (4.5c) уединим вторую производную в левой части уравнения Шредингера (6):
Если все величины в правой части ограничены:
то из (4.6) следует ограниченность второй производной волновой функции. Отсюда, в свою очередь, вытекает непрерывность 

Приступим к решению задачи. Введём волновые числа
с которыми уравнения (4.3) и (4.4) преобразуются в
Первое уравнение имеет осциллирующие решения, аналогичные (3.1). Но сейчас нам удобнее перейти к их экспоненциальному представлению с мнимой единицей:
Решение второго уравнения — линейная комбинация убывающей и растущей экспонент:
Граничные условия (4.5) дают три уравнения:
С их помощью константы A и B могут быть выражены через C:
Мы ввели обозначения
Таким образом, в области x
Оно представляет сложение двух волн равной амплитуды. Первое слагаемое описывает падающую волну, второе — отражённую, их сумма — стоячую волну.
Перейдём к области x > 0, запрещённой для движения классической частицы. Константу C удобно выразить через параметры a и j :
Решением здесь является экспоненциально затухающая функция
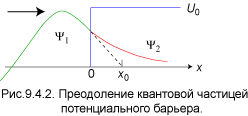
На расстоянии x0 = 1/k2 она убывает в e раз. Соответственно, вероятность обнаружить частицу на расстоянии x0 от порога равна |Ψ2| 2 ≈ 0.1. Рис. 9.4.2 иллюстрирует полученное решение. Потенциальный барьер помечен синим цветом. Слева от границы барьера осциллирующая часть волновой функции Ψ1 изображена зелёной кривой, а красная линия справа обозначает экспоненциально затухающую функцию Ψ2 . Пунктиром показана касательная к волновой функции в
начале координат. Она пересекает горизонтальную ось в точке x = x 0.
Формула (4.9) показывает, что квантовая частица может проникать сквозь потенциальный барьер даже в том случае, когда её энергия E меньше его высоты U0. В пределе классической физики величина x0 стремится к нулю вместе с постоянной Планка:
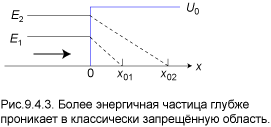
Чем больше энергия E частицы, тем дальше проникает она в классически запрещённую область движения. Если мы будем увеличивать энергию E, приближая её к U0, то, согласно (4.10), величина x0 неограниченно растёт. Это соответствует классическим представлениям о том, что частица с энергией E ≥ U0 должна беспрепятственно проходить потенциальный барьер. Схематически
зависимость x0 от E представлена на рис. 9.4.3.
Попробуем обнаружить частицу в окрестности точки x0, например, «подсветив» её фотоном. Частица будет локализована в пространстве с точностью
Согласно соотношению неопределённостей Гайзенберга , мы сообщим ей импульс
то есть, частица приобретает дополнительную энергию
позволяющую преодолеть потенциальный барьер. Таким образом, «подсвеченную» частицу можно обнаружить в области, недоступной для классического движения; но её энергия окажется выше пороговой.
Уравнение шредингера в потенциальном ящике
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
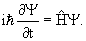 | (4.1) |
где 
в которой 







х → 


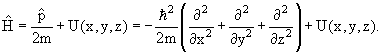 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


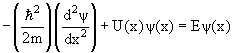
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
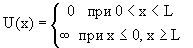 | (4.5) |
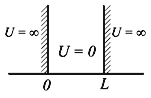
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
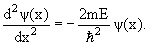 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
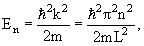 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
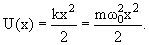 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
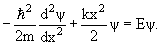 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
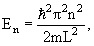

Одномерный гармонический осциллятор:
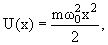
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
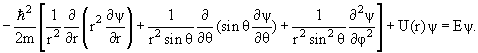 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
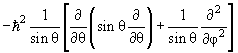 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 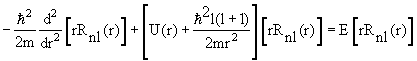 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
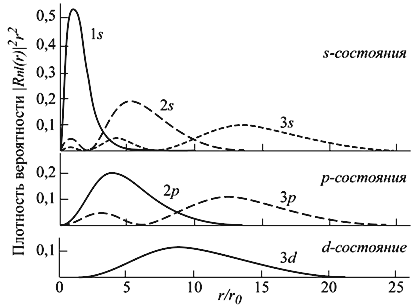
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
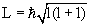 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
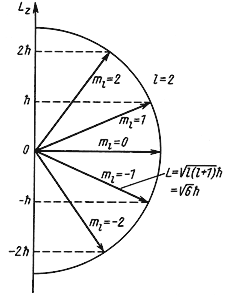
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
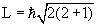
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Уравнение Шредингера (общие свойства)
№1 Стационарное уравнение Шредингера имеет вид 
Стационарное уравнение Шредингера в общем случае имеет вид




Линейного гармонического осциллятора
ü Частицы в одномерном потенциальном ящике с бесконечно высокими стенками
Частицы в трехмерном потенциальном ящике с бесконечно высокими стенками
Электрона в атоме водорода
Установите соответствия между квантовомеханическими задачами и уравнениями Шредингера для них.
Общий вид стационарного уравнения Шредингера имеет вид:


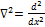
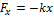

Значение потенциальной энергии электрона в потенциальном ящике с бесконечно высокими стенками U=0.Электрон в водородоподобном атоме обладаем потенциальной энергией 
Таким образом, для электрона в одномерном потенциальном ящике ур-ие Шредингера имеет вид:
С помощью волновой функции ,являющейся решением уравнения Шредингера ,можно определить….
Варианты ответа: (Укажите не менее двух вариантов ответа)
Средние значения физических величин ,характеризующих частицу
Вероятность того,что частица находится в определенной области пространства
Величина 
Уравнение Шредингера (конкретные ситуации)
№1Собственные функции электрона в одномерном потенциальном ящике с бесконечно высокими стенками имеют вид 

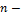

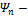


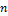
Число узлов 

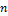


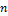
Ядерные реакции.
№1В ядерной реакции 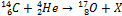
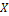
Из законов сохранения массового числа и зарядового числа следует, что заряд частицы равен нулю, а массовое число равно 1. Следовательно, буквой 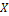
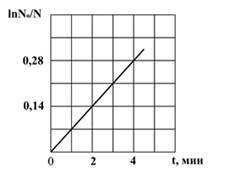
На графике в полулогарифмическом масштабе показана зависимость изменения числа радиоактивных ядер изотопа 
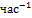
Число радиоактивных ядер изменяется со временем по закону 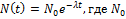
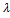
ln 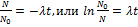

Законы сохранения в ядерных реакциях.
Реакция 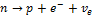
Во всех фундаментальных взаимодействиях выполняются законы сохранения: энергии, импульса, момента импульса (спина) и всех зарядов (электрического 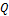
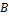
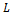
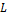
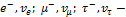
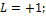

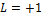
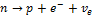
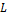
ü Лептонного заряда
Спинового момента импульса
Реакция 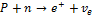
Во всех фундаментальных взаимодействиях выполняются законы сохранения: энергии,импульса,момента импульса(спина)и всех зарядов(электрического Q,барионного B и лептонного L).Эти законы сохранения не только ограничивают последствия различных взаимодействий,но определяют также все возможности этих последствий. Согласно закону сохранения барионного заряда B,для всех процессов с участием барионов и антибарионов суммарный барионный зарад сохраняется. Барионам (нуклонам n,p и гиперонам)приписывается барионный заряд
B=-1,а всем остальным частицам барионный заряд-B=0.Реакция 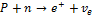
Варианты ответа: 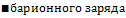
Законом сохранения электрического заряда запрещены реакции…
Варианты ответа(не менее 2):
При взаимодействии элементарных частиц и их превращении в другие возможны только такие процессы,в которых выполняются законы сохранения,в частности закон сохранения электрического заряда:суммарный электрический заряд частиц,вступающих в реакцию,равен суммарному электрическому заряду частиц,полученных в результате реакции.Электрический заряд Q в единицах элементарного заряда равен:у нейтрона (n) Q=0,протона (P) Q=+1, электрона ( 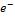
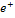
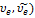
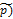


№1Известно четыре вида фундаментальных взаимодействий. В одном из них участниками являются все заряженные частицы, обладающие магнитным моментом, переносчиками –фотона. Этот вид взаимодействия характеризуется сравнительной интенсивностью 
Все перечисленные характеристики соответствуют электромагнитному взаимодействию. Его радиус действия равен бесконечности.
ü
http://nuclphys.sinp.msu.ru/sem2/sem04.html
http://zdamsam.ru/a38341.html