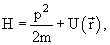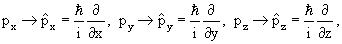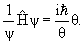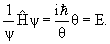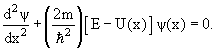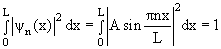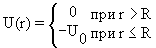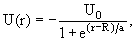Уравнение шредингера в сферических координатах
Понятие о стационарной атомной орбите электрона возникает из решения уравнения Шредингера. Что это за уравнение и как его получить?
Его можно вывести из выражения для обобщенной плоской волны:
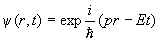
где ћ = h/2π — постоянная Планка, p — импульс и E — энергия. Если волновую функцию ψ один раз продифференцировать по времени и дважды по координатам:
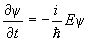
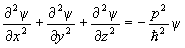
а затем эти выражения приравнять по Eψ, помня, что E = p 2 /2m, то в результате и получим уравнение Шредингера, которое удобно переписать через оператор Ñ :
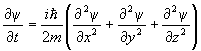
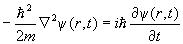
Среди всех решений данного уравнения имеются решения, зависящие только от времени:
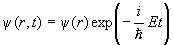
Если это решение подставить в уравнение Шредингера, то оно и будет давать для электронов стационарные орбиты, зависящие только от переменной r :
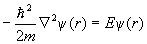
В центрально-симметричном кулоновском поле с потенциалом V = –Ze 2 /r уравнение Шредингера обычно представляют очень коротко через оператор Гамильтона H:
Hψ =Eψ, так как 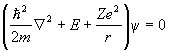
то 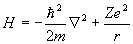
Симметрия поля диктует соответствующую систему координат, а именно, сферическую:
x = r sin θ cos φ, y = r sin θ sin φ, z = r cos θ,
где r — радиус-вектор полярных координат, θ — полярный угол, φ — азимут.
В сферических координатах уравнение Шредингера запишется в виде:
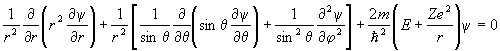
Это уравнение с разделяющимися переменными по радиальной составляющей R и угловой Y имеет решение в форме произведения этих составляющих, т.е.
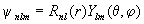
В этом виде волновая функция зависит от трех параметров:
n — главное квантовое число;
l = <0, 1, 2, …, n – 1> — орбитальное квантовое число;
m = <–l , –l + 1, –l + 2, … , 0, 1, 2, …, l – 2, l – 1, l > — магнитное квантовое число.
Радиальная часть волновой функции зависит от присоединенных полиномов Лагерра, которые имеют следующий аналитический вид для n = 1, 2, 3:
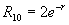
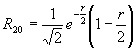
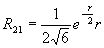
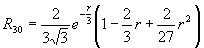
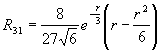
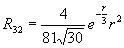
Примерный ход зависимости R от r показан на рис. 27а. Угловая часть волновой функции зависит от присоединенных полиномов Лежандра, которые имеют следующий аналитический вид для l = 0, 1, 2, 3:
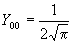
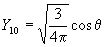
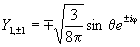
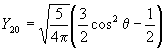
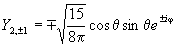
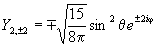
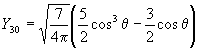
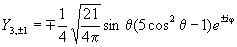
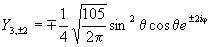
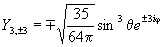
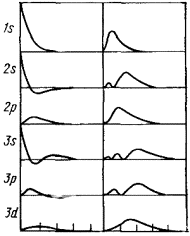
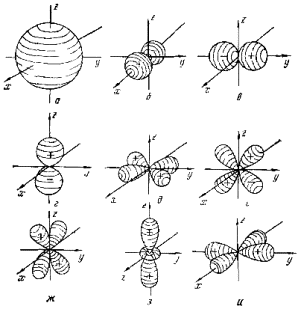
Зависимости Y от θ и φ показаны на рис. 27б. Угловая составляющая определяет симметрию электронного уровня, а значит, и пространственную группу преобразований, которая оставляет электрон на этом уровне без изменений. Решениями уравнения являются не только сами значения, но и их линейная комбинация, что позволяет избавиться от мнимых величин. Например, комбинация из 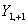
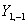
В табл. 23 приведены симметризованные функции для s, p и d орбиталей электронов.
| Орбиты | Симметрия |
| s | 1 |
| px | sin θ cos φ |
| py | sin θ sin φ |
| pz | cos θ |
| dxy | sin 2 θ sin 2φ |
| dxz | sin 2θ cos φ |
| dyz | sin 2θ sin φ |
| dx 2 – y 2 | sin 2 θ cos 2φ |
| dz 2 | 3cos 2 θ – 1 |
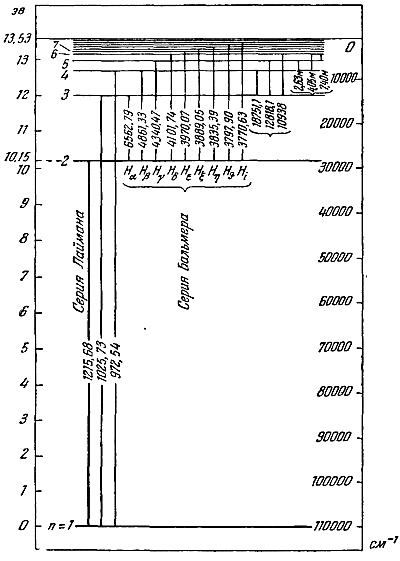
Если волновые функции ψnlm определяют собственные векторы, то собственными значениями выступают энергии электронов, зависящие только от главного квантового числа по известной из модели Бора формуле:
En = 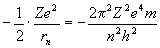
Частота излучаемой или поглощаемой электромагнитной волны определяется тоже по известной формуле Бальмера:
fmn = (En – Em)/h = 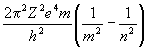
= 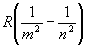
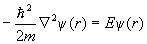
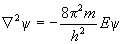
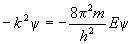
В последнем уравнении сократим ψ и выразим энергию E, получим
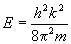
Перед нами квадратичный закон дисперсии E(k), играющий центральную роль в теории энергетических уровней электронов в кристаллах полупроводников и металлов. Слово дисперсия с латинского переводится как рассеяние. Следовательно, закон дисперсии E(k) следует понимать как закон рассеяния периодического процесса. Так, звуковые волны при прохождении через среду изменяют свою форму, что называется акустической дисперсией. На дисперсию света влияет коэффициент преломления среды, который будет различным для различных длин волн. В частности, белый свет рассеивается на свои составные части, т.е. мы наблюдаем его спектральное разложение. Явление рассеяния наблюдается также при дифракции и интерференции волн любой природы. Коль скоро волновые функции электронов представляются плоскими или сферическими волнами, то и их дисперсия, т.е. рассеяние, на узлах кристаллической решетки есть вполне естественный физический процесс.
С точки зрения аналитической геометрии, квадратичный закон дисперсии представляет собой уравнение сферы в k-пространстве, которое пока для нас остается тайной. Значит, изоэнергетические поверхности или поверхности постоянной энергии будут представлять собой сферы. Прежде чем уяснить, что такое пространство k, необходимо понять, через что выражается число k. Для этого выразим кинетическую энергию электрона посредством импульса:
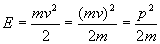
Приравняв оба выражения для энергии, мы понимаем смысл волнового числа k:
Если вспомнить о длине волны де Бройля: λ = h/mv = h/p, то окончательно для волнового числа получим выражение: k = 2π/λ. Таким образом, волновое число k — это число длин волн, укладывающихся на длине окружности, выраженной в радианах, т.е. на длине 2π.
Данное представление о длине волны ассоциируется с представлением о круговой частоте ω = 2π/Т, для которой T есть период колебания какой-либо физической величины во времени t. По аналогии, волновое число k отражает пространственную круговую частоту, т.е. колебание какой-либо физической величины, распределенной в пространстве r. Такая периодичность возникает в твердых веществах, имеющих кристаллическую решетку с периодом a.
Поэтому для кристаллических веществ волновое число приобретает новое содержание: во-первых, его записывают как k = 2π/a; во-вторых, волновое число становится вектором, поскольку узлы решетки существуют в пространстве трех измерений (далее под k мы будем всегда понимать именно вектор, поэтому не станем его каким-либо образом выделять). Так возникает понятие о k-пространстве, которое является обратным по отношению к r-пространству.
Подобно тому, как периодические функции во времени f(t) = f(t + T) часто выражают через преобразование Фурье, получая спектральную характеристику F(ω), точно так же периодические функции в пространстве f(r) = f(r + R) удобно представлять через преобразование Фурье в k-пространстве. Таким образом, закон дисперсии E(k) — это спектр энергии.
Если бы речь шла об энергетическом спектре в виде E(ω), то смысл данной зависимости состоял бы в следующем. Числовые значения E(ω1), E(ω2), …, E(ωn) говорили бы о значениях энергии, приходящихся на частоты и ω1, ω2, …, ωn какого либо периодического процесса. Например, частота рентгеновского излучения способна переносить большую энергию, а частота видимого света — малую.
По аналогии дискретные значения энергии в k-пространстве E(k1), E(k2), …, E(kn) говорят о распределении энергии в обратном пространстве кристалла по конкретным значениям волнового вектора k1, k2, …, kn. В частности, энергия электронов может зависеть от направления волнового вектора в решетке при равном его модуле, что вызвано анизотропией кристалла. Квадратичный закон дисперсии, дающий сферическую поверхности в k-пространстве, говорит об отсутствии анизотропии; этот закон и был получен для свободных электронов, находящихся вне кристалла.
Поскольку кристаллические решетки могут быть различными, то в законе дисперсии E(k) будет присутствовать так называемый структурный фактор S(K), определяемый конкретной конфигурацией решетки. Потенциал кулоновского поля атомов, образующих решетку, определяет форм-фактор v(K), который тоже будет принимать различные значения для различных атомов, входящих в данную решетку. Таким образом, закон дисперсии E(k) выражается как некая комбинация структурного фактора S(K) и форм-фактора v(K).
Структурный фактор часто задается той или иной матрицей, в которой имеются нулевые и ненулевые матричные элементы. В этом случае форм-фактор выступает в виде числовых значений матричных элементов. Вид матрицы для сходных материалов, например кремния и германия, будет одинаковым, но величины матричных элементов для них – различны. Матричные элементы зависят также от координат k-пространства, как функция от аргумента.
Полный закон дисперсии E(k) определяется всеми собственными значениями матрицы, описывающей данную электронную систему, для каждой точки k-пространства. На практике часто бывает достаточно определить закон дисперсии в определенных направлениях k-пространства или даже в нескольких характерных точках, причем берут не все, а только несколько нижних собственных значений (верхние уровни энергии, лежащие в зоне проводимости высоко над запрещенной зоной, чаще всего не интересуют практиков).
Далее нам понадобится еще одно важное понятие, непосредственно вытекающее из закона дисперсии E(k), который для реальных материалов отличается от сферической формы. Однако введенное ниже понятие остается в силе и тогда, когда закон дисперсии не носит квадратичную зависимость от волнового вектора. Итак, найдем первую, затем вторую производную энергии по волновому вектору k, когда закон дисперсии задан квадратичной формулой, и выразим массу:
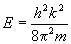
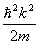
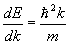
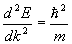
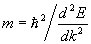
Вторая производная характеризует кривизну поверхности закона дисперсии E(k). У нас получилось, что масса электрона обратно пропорциональна кривизне закона дисперсии. Чем больше кривизна, тем меньше масса и, наоборот. Так как уравнение E(k) представляло сейчас сферу, поверхность которой имеет постоянную кривизну, то куда бы ни летел электрон, он будет иметь постоянную массу, равную массе свободного электрона. Но в кристалле функция E(k) не квадратична, изоэнергетические поверхности отличаются от сферических и, следовательно, масса электрона зависит от направления в k-пространстве и величины второй производной от энергии. Скалярная величина массы превращается в тензорную величину, которая называется эффективной массой:
если d 2 E/dk 2 > 0, то m > 0; если d 2 E/dk 2 2 E/dk 2 = 0, что соответствует бесконечно большому значению массы электрона или дырки. Никакая сила не способна перенести частицы с массой m = ± ∞; отсюда следует, что понятие эффективной массы имеет физическое значение вблизи нижнего края зоны проводимости для электронов и вблизи верхнего края валентной зоны для дырок.
Уравнение шредингера в сферических координатах
Аналог классического волнового уравнения был предложен Э. Шредингером в 1925 г. Как и классическое уравнение, уравнение Шредингера связывает производные волновой функции по времени и координате. Уравнение Шредингера описывает поведение любых нерелятивистских систем. На примерах частицы, находящейся в бесконечно глубокой яме, и гармонического осциллятора рассмотрены простейшие квантовые системы, получены дискретные спектры состояний. Возможности описания динамики данных систем ограничены набором квантовых чисел, отражающих универсальные и внутренние симметрии квантовых систем.
4.1. Уравнение Шредингера
В квантовой физике изменение состояния частицы описывается уравнением Шредингера
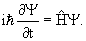 | (4.1) |
где 
в которой 







х → 


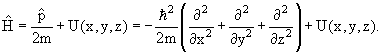 | (4.2) |
Уравнение Шредингера
Зависящее от времени уравнение Шредингера:
где 
Разделение переменных. Запишем Ψ(




Левая часть является функцией только координат, а правая не зависит от переменной x. Поэтому обе части последнего уравнения должны быть равны одной и той же постоянной, которую обозначим E
θ(t) = exp(−iEt/ћ), 




Уравнение 


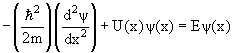
Для трехмерной системы с массой m в поле с потенциалом U(
−(ћ 2 /2m)Δψ(



где Δ – лапласиан.
Так как уравнение Шредингера является линейным уравнением первого порядка по времени, то с его помощью по заданному значению волновой функции Ψ(x, y, z, 0) в момент времени t = 0 можно найти её значение в произвольный момент времени t − Ψ(x, y, z, t).
Уравнение Шредингера для стационарного состояния, когда потенциальная энергия частицы не зависит от времени, имеет вид
 ψ( ψ( ) = Eψ( ) = Eψ( ). ). | (4.3) |
Это уравнение называют стационарным уравнением Шредингера.
Так как в стационарном состоянии
Ψ( ,t) = ψ( ,t) = ψ( )exp(−iEt/ћ) )exp(−iEt/ћ) | (4.4) |
и вероятность найти частицу в момент t в точке x, y, z пропорциональна |Ψ(
|ψ(x,y,z)| 2 , т.е. не зависит от времени. Аналогично, вероятность обнаружить значение физической величины, характеризующей систему, также не изменяется со временем, поскольку выражается через квадрат модуля волновой функции.
4.2. Частица в одномерной прямоугольной яме с бесконечными стенками
Потенциальная энергия U(x) в прямоугольной яме удовлетворяет следующим условиям:
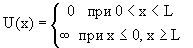 | (4.5) |
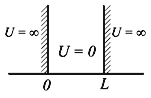
Рис.4.1. Прямоугольная яма с бесконечными стенками
Частица находится в области 0 ≤ x ≤ L. Вне этой области ψ(x) = 0. Уравнение Шредингера для частицы, находящейся в области 0 ≤ x ≤ L
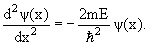 | (4.6) |
Волновая функция, являющаяся решением уравнения (4.9), имеет вид
| ψ(x)= Аsin kx + Bcos kx, | (4.7) |
где k = (2mE/ћ 2 ) 1/2 . Из граничных условий ψ(0) = 0, ψ(L) = 0 и условий непрерывности волновой функции следует
| Аsin kL = 0. | (4.8) |
kL = nπ, n = 1, 2, 3, … , то есть внутри потенциальной ямы с бесконечно высокими стенками устанавливаются стоячие волны, а энергия состояния частиц имеет дискретный спектр значений En
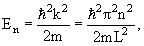 n = 1, 2, 3, … n = 1, 2, 3, … | (4.9) |
Частица может находиться в каком-то одном из множества дискретных состояний, доступных для неё.
Каждому значению энергии En соответствует волновая функция ψn(x), которая с учетом условия нормировки
 | (4.10) |
В отличие от классической, квантовая частица в прямоугольной яме не может иметь энергию
E 2 π 2 /(2mL 2 ). Состояния частицы ψn в одномерном поле бесконечной потенциальной ямы полностью описывается с помощью одного квантового числа n. Спектр энергий дискретный.
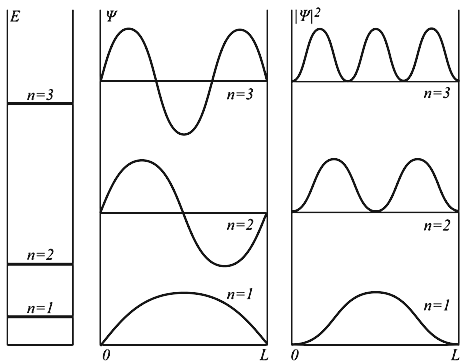
Рис. 4.2. Уровни энергии и волновые функции частицы Ψ в бесконечной прямоугольной яме. Квадрат модуля волновой функции |Ψ| 2 определяет вероятность нахождения частицы в различных точках потенциальной ямы.
4.3. Гармонический осциллятор
Положение уровней частицы в потенциальной яме зависит от вида потенциальной ямы. В одномерной потенциальной яме гармонического осциллятора потенциальная энергия имеет вид
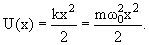 | (4.11) |
В этом случае одномерное уравнение Шредингера имеет вид
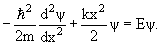 | (4.12) |
Допустимые значения полной энергии определяются формулой
| En = ћω0(n + 1/2), n = 0, 1, 2, | (4.13) |
В отличие от бесконечной прямоугольной ямы, спектр уровней гармонического осциллятора эквидистантный.
С увеличением массы частицы или размеров области ее локализации квантовое описание частицы переходит в классическое.
Частица в одномерной потенциальной яме
Одномерная прямоугольная яма шириной L:
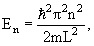

Одномерный гармонический осциллятор:
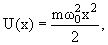
4.4. Частица в поле с центральной симметрией
В сферических координатах стационарное уравнение Шредингера для частицы в центральном потенциале U(r) имеет вид
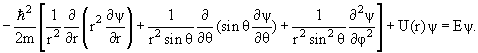 | (4.14) |
Решение уравнения (4.14) записываются в виде произведения радиальной и угловой функций
| ψ(r,θ,φ) = Rnl(r)Ylm(θ,φ), | (4.15) |
где радиальная функция Rnl(r) и угловая функция Ylm(θ,φ), называемая сферической, удовлетворяют уравнениям
 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 2 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) | (4.16) |
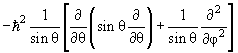 Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) Ylm(θ,φ) = ћ 2 l(l +1)Ylm(θ,φ) 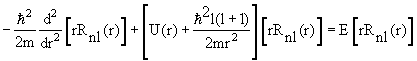 | (4.17) |
Уравнение (4.16) определяет возможные собственные значения l и собственные функции Ylm(θ,φ) оператора квадрата момента 
Схема уровней (последовательность и абсолютные значения энергий) зависит от радиальной функции Rnl(r), которая в свою очередь определяется потенциалом U(r), в котором находится частица.
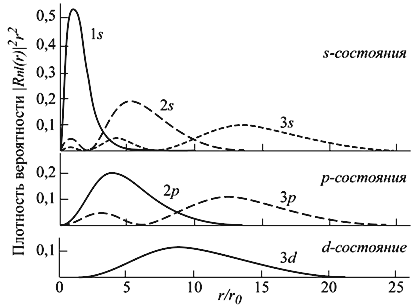
Рис. 4.3. Радиальное распределение вероятности нахождения электрона в кулоновском поле протона (атом водорода). Расстояния даны в боровских радиусах
r0 = ћ 2 /mee 2 ≈ 0.529·10 8 cм.
| Решения уравнения |
существуют лишь при определенных значениях квантовых чисел n (радиальное квантовое число), l (орбитальное квантовое число) и m (магнитное квантовое число).
Возможные энергетические состояния системы (уровни энергии) определяются числами n и l и в случае сферически симметричных состояний не зависят от квантового числа m. Число n может быть только целым:
n = 1, 2, …, ∞. Число l может принимать значения 0, 1, 2, …, ∞.
4.5. Орбитальный момент количества движения
Собственные значения L 2 и Lz являются решением уравнений


Они имеют следующие дискретные значения
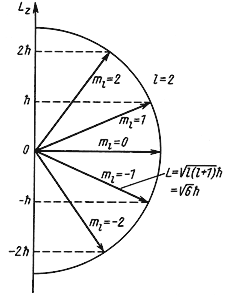
L 2 = ћ 2 l(l + 1), где l = 0, 1, 2, 3, …,
Lz = ћm, где m = 0, ± 1, ± 2, ± 3,…, ± l.
Для характеристики состояний с различными значениями орбитального момента l обычно используют следующие обозначения:
Спектроскопические названия орбитальных моментов l
| l = 0 | s-состояние |
| l = 1 | p-состояние |
| l = 2 | d-состояние |
| l = 3 | f-состояние |
| l = 4 | g-состояние |
| l = 5 | h-состояние |
| и. т. д. |
Состоянию с l = 0 отвечает сферически симметричная волновая функция. В тех случаях, когда l ≠ 0 волновая функция не имеет сферической симметрии. Симметрия волновой функции определяется симметрией сферических функций Ylm(θ,φ). Имеет место интересное квантовое явление, когда решение сферически симметричной задачи (потенциал описывает сферически симметричную систему) приводит к состояниям, не обладающим сферической симметрией. Таким образом, симметрия уравнений не обязательно должна отражаться в симметрии каждого отдельно взятого решения этих уравнений, а лишь во всей совокупности этих решений.
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L:
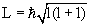 | (4.18) |
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной квантовое число l, имея в виду, что между l и L имеется однозначная связь (4.18).
Рис. 4.4 Возможные ориентации вектора 
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения L квантуется. Например, для частицы с l = 2 момент количества движения
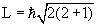
= 6.58·10 -22 √6 МэВ·сек ≈ 2.6·10 — 34 Дж·сек.
Пространственное квантование. Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения квантуется, то и направление 

Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m.
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии определяет возможные значения квантовых чисел. Очевидно, что система, описываемая функцией e im φ , примет прежнее значение только тогда, когда азимутальный угол φ в результате поворота вокруг оси z примет прежнее значение φ. Этому условию функция e im φ удовлетворяет только в случае, когда величина mφ кратна 2π. Т.е. величина m должна иметь целые значения. Так как необходимо учитывать вращение в двух противоположных направлениях и отсутствие вращения, единственно возможными значениями оказываются m = 0, ±1, ±2, … .
4.6. Спин
Спин − собственный момент количества движения частицы. Между значением вектора спина 

 2 = ћ 2 s(s + 1) 2 = ћ 2 s(s + 1) | (4.19) |
В отличие от орбитального квантового числа l, которое может быть лишь целым числом или нулем, спиновое квантовое число s (в дальнейшем просто спин) может быть как целым (включая нуль), так и полуцелым, т. е. s = 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы спин может принимать единственное присущее этому типу частиц значение. Так, спины π-мезонов и К-мезонов равны 0. Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Бозоны составляют класс частиц с целым значением спина, спин фермионов имеет полуцелое значение. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая характеристика.
Как и в случае других квантовых векторов, проекция вектора спина 
szћ = ±sћ, ±(s − 1)ћ, ±(s − 2)ћ. ±1/2ћ или 0.
Число sz − это квантовое число проекции спина. Максимальная величина sz совпадает с s. Так как спин электрона равен 1/2, то проекция этого спина может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция -1/2, то говорят, что спин направлен вниз.
4.7. Полный момент количества движения
Полный момент количества движения частицы или системы частиц 





Квадрат полного момента имеет значение:

Квантовое число полного момента j, соответствующее сумме двух векторов 

j = l + s, l + s −1. |l − s|
Проекция 
Число значений проекции Jz равно 2j + 1. Если для 

4.8. Квантовые числа
Квантовые числа – это целые или дробные числа, которые определяют все возможные значения физической величины, характеризующей различные квантовые системы – атомы, атомные ядра, кварки и другие частицы.
Таблица квантовых чисел
| n | Радиальное квантовое число. Определяет число узлов волновой функции и энергию системы. n = 1, 2, …, ∞. |
| J, j | Полный угловой момент J и его квантовое число j. Последнее никогда не бывает отрицательным и может быть целым или полуцелым в зависимости от свойств рассматриваемой системы.  2 = ћ 2 j(j + 1). 2 = ћ 2 j(j + 1). |
| L, l | Орбитальный угловой момент L и его квантовое число l. Интерпретация l такая же, как j, но l может принимать только целые значения, включая нуль: l = 0, 1, 2,…. L 2 = ћ 2 l(l + 1). |
| m | Магнитное квантовое число. Проекция полного или орбитального углового момента на выделенную ось (обычно ось z) равна mћ. Для полного момента m = ±j, ±(j-1), …, ±1/2 или 0. Для орбитального m = ± l, ± (l-1), …, ±1, 0. |
| S, s | Спиновый угловой момент S и его квантовое число s. Оно может быть либо положительным целым (включая нуль), либо полуцелым. s – неизменная характеристика частицы определенного типа. S 2 = ћ 2 s(s + 1). |
| sz | Квантовое число проекции спинового момента частицы на выделенную ось. Эта проекция может принимать значения szћ, где sz = ± s, ± (s -1), …, ±1/2 или 0. |
| P или π | Пространственная четность. Характеризует поведение системы при пространственной инверсии  → — → —  (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. (зеркальном отражении). Полная четность частицы Р = π(-1) l , где π – её внутренняя четность, а (-1) l – её орбитальная четность. Внутренние четности кварков положительные, антикварков — отрицательные. |
| I | Изоспин. Характеризует свойство зарядовой инвариантности сильных взаимодействий |
Для обозначения спинового момента часто используют букву J.
Все состояния, в которых может находиться квантовая система, описываются с помощью полного набора квантовых чисел. Так в случае протона в ядре состояние протона описывается с помощью четырех квантовых чисел, соответствующих четырем степеням свободы – трем пространственным координатам и спину. Это
- Радиальное квантовое число n ( 1, 2, …, ∞),
- Орбитальное квантовое число l (0, 1, 2, …),
- Проекция орбитального момента m (± l, ± (l-1), …, ±1, 0),
- Спин протона s =1/2.
Для описания сферически-симметричных систем в квантовой физике используются различные сферически симметричные потенциалы с различной радиальной зависимостью:
- Кулоновский потенциал U = Q/r,
- Прямоугольная потенциальная яма
- Потенциал типа гармонического осциллятора U = kr 2 ,
- Потенциал Вудса-Саксона (с его помощью описываются внутриядерные взаимодействия):
где U0, а и R – положительные константы (R – радиус ядра). Во всех случаях сферически симметричные системы можно описать с помощью набора квантовых чисел n, l, j, jz, однако, в зависимости от радиального вида потенциала энергетический спектр состояний системы будет различным.
Существование сохраняющихся во времени физических величин тесно связано со свойствами симметрии гамильтониана системы. Например, в случае, если квантовая система обладает центральной симметрией U = U(r), то этой системе соответствует сохранение орбитального момента количества движения l и одной из его проекций m. При этом из-за сферической симметрии задачи энергия состояний не будет зависеть от величины m, т. е. состояния будут вырожденными по m.
Наряду с пространственными симметриями, связанными с непрерывными преобразованиями, в квантовой физике существуют и другие симметрии – дискретные. Одной из них является зеркальная симметрия волновой функции относительно инверсии координат (

Система тождественных частиц характеризуется еще одной симметрией – симметрией относительно перестановок тождественных частиц. Эта симметрия определяется свойствами частиц, образующих систему. Системы частиц с целым спином (бозонов) описываются симметричными волновыми функциями, системы частиц с полуцелым спином (фермионов) − антисимметричными волновыми функциями.
Задачи
4.1. Вычислите допустимые уровни энергии электрона, находящегося в одномерной прямоугольной потенциальной яме шириной 10 -8 см, протона, находящегося в потенциальной яме 5 Фм, и шарика массой 1 г, находящегося в потенциальной яме 1 см.
4.2. Рассчитать энергию перехода между состояниями 1s и 2s в атоме водорода.
4.3. Найти значение полного момента j для протона в d-состоянии. Каким будет результат измерения полного момента протона в состоянии 1d5/2?
4.4. Найти полный момент (квантовое число j) системы двух нуклонов в s‑состоянии (l = 0).
4.5. Какие значения может иметь полный момент системы j, если
А. Нейтрон и протон находятся в состояниях с |l,s:j>n = |1, 1 /2: 3 /2>, |l,s:j>p = |1, 1 /2: 3 /2>?
Б. Два нейтрона находятся в состояниях с |l,s:j>1 = |1, 1 /2: 3 /2> и |l,s:j>2 = |1, 1 /2: 3 /2>?
4.6. А) Нейтрон находится в p-состоянии. Найти значения полного момента j и возможные значения проекции момента jz. Каким будет результат измерения орбитального момента частицы в этом состоянии? Б) Рассмотрите задачу А) для протона в d-состоянии.
Ответ: А) j = 3/2, 1/2; jz = ±3/2, ±1/2; L = ћ√ l(l +1) = √ 2 ћ;
Б) j = 5/2, 3/2; jz = ±5/2, ±3/2, ±1/2; L = ћ√ l(l +1) = √ 6 ћ
4.7. А) Частица с собственным моментом s = 3/2 находится в состоянии с орбитальным моментом
l = 2. Найти полный момент частицы j.
Б) Частица с собственным моментом s = 1/2 находится в состоянии с орбитальным моментом
l = 3. Определите полный момент частицы j
Ответ: А) j = 7/2 ÷ 1/2; Б) j = 7/2, 5/2
4.8. Протон и нейтрон находятся в состоянии с относительным орбитальным моментом L = 1. Найти полный момент системы J.
Ответ: J = 0, 1, 2
4.9. На оболочке с квантовым числом n = 1, l = 2 находятся протон и нейтрон. Определить их суммарный полный момент J и его проекцию Jz. Изменится ли результат, если на оболочке n = 1,
l = 2 будут находиться два нейтрона?
4.10. Почему возникают вырожденные состояния?
4.11. Написать оператор Гамильтона 
4.12. Напишите стационарное уравнение Шредингера в сферической системе координат.
4.13. Какие квантовые числа характеризуют частицу в центрально-симметричной потенциальной яме?
4.14. Покажите, что волновые функции ψ = Aexp(kx −ωt) и ψ = Asin(kx −ωt) не удовлетворяют зависящему от времени уравнению Шредингера.
4.15. Покажите, что волновые функции ψ = Ae i(kx −ωt) и ψ = A(cos(kx −ωt) − sin(kx −ωt))удовлетворяют зависящему от времени уравнению Шредингера.
4.16. Частица находится в низшем состоянии n = 1 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L.
А) Рассчитайте вероятность обнаружить частицу в интервале Δx = 0.001L при x = 1 /2L, x = 2 /3L, x = L.
Б) Рассмотрите случай, когда частица находится в состоянии n = 2 при тех же значениях x.
Ответ: А) P(L/2) = 0.002; P(2L/3) = 0.0015; P(L) = 0; Б) P(L/2) = 0; P(2L/3) = 0.0015; P(L) = 0
4.17. Частица находится в состоянии n = 2 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить частицу в интервале ( 1 /3L, 2 /3L).
Ответ: P(L/3, 2L/3) = 0.2
4.18. Электрон находится всостонии n = 5 в бесконечно глубокой одномерной прямоугольной потенциальной яме размера L. Рассчитайте вероятность обнаружить электрон в области x от 0.2L до 0.5L.
Ответ: P(0.2L, 0.5L) = 0.3
4.19. Электрон находится в бесконечно глубокой одномерной потенциальной яме. Рассчитайте ширину потенциальной ямы, если энергия состояния n = 1 равна 0.1 эВ.
Ответ: L = 1.9 нм
4.20. Рассчитайте средние значения и 2 > для состояний n = 1, 2, 3 в бесконечно глубокой прямоугольной потенциальной яме.
4.21. Что общего и в чем различие в описании атома водорода в теории Шредингера и в модели Бора?
4.22. Почему энергии атома водорода в теории Шредингера не зависят от орбитального квантового числа l?
4.23. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Ответ: Lz = -3ћ, -2ћ. 3ћ; L 2 = 12ћ 2
4.24. Угловой момент характеризуется квантовым числом l = 3. Какие значения могут принимать Lz и L 2 ?
Уравнение Шредингера в сферических координатах
Центральносимметричные и
Осесимметричные СТАЦИОНАРНЫЕ системы
Гамильтониан стационарной системы
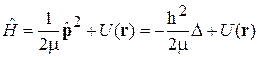
Центральная симметрия означает отсутствие в сферических координатах угловой зависимости
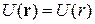
Осевая симметрия означает отсутствие в цилиндрических координатах угловой зависимости

Особенностью центрально- и осесимметричных систем является сохранение момента импульса.
Уравнение Шредингера в сферических координатах
Гамильтониан центрально-симметричной системы складывается из кинетических энергий радиального и углового движений и из потенциальной энергии. С учетом (5.1), (4.8) и (4.9) получаем
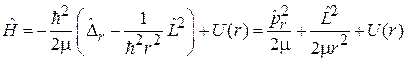
Из (4.5) и (5.7) находим
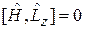
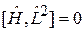
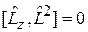
Момент импульса и одна из его проекций сохраняются с течением времени и имеют определенные значения вместе с энергией. Состояние характеризуется собственными значениями операторов 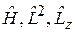
Радиальный импульс. Из (4.9)
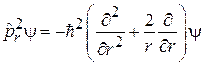
Уравнение Шредингера 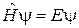

Решение ищем в виде
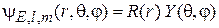
Подстановка в уравнение, умноженное на 2μr 2 и деленное слева на ψ, дает
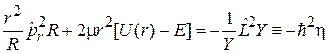
Уравнение для 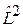
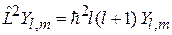
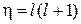
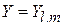
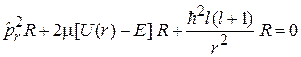
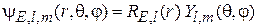
Радиальное уравнение с учетом (5.8) получает вид
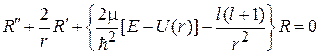
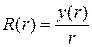
с учетом 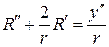

где 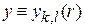
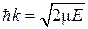
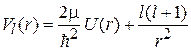
– эффективная потенциальная энергия включает центробежную энергию отталкивания от оси вращения.
Конечность 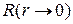
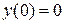
Условие ортонормированности (5.6) для дискретного спектра

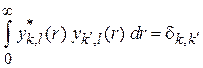
Для уравнения (5.12) и решения 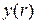
http://nuclphys.sinp.msu.ru/sem2/sem04.html
http://mydocx.ru/1-58180.html