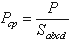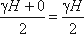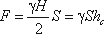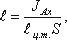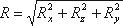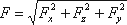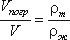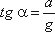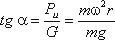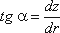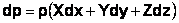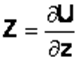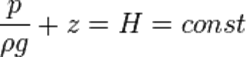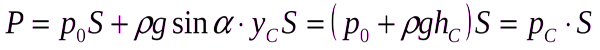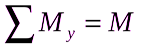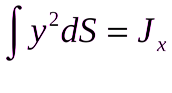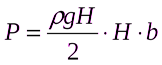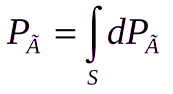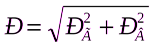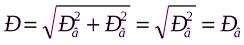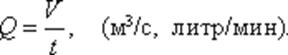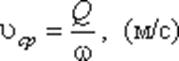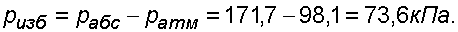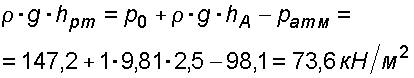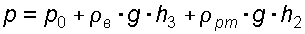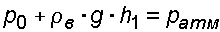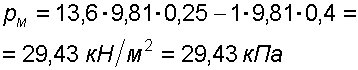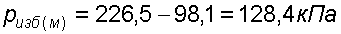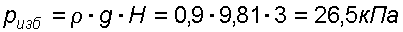Уравнение силы давления на плоские стенки

Уравнение силы давления на плоские стенки

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

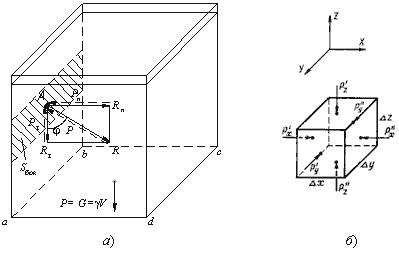
Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.

Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара площадку S_бок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный R_n (перпендикулярный к заштрихованной площадке) и касательный R_τ к стенке.

Сила нормального давления R_n вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила R_τ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая R_τ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления P_x, P_y , P_z на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P’_x, P’_y, P’_z, а вектора давлений, действующие в обратном направлении соответственно P»_x, P»_y, P»_z. Поскольку кубик находится в равновесии, то можно записать равенства

где γ — удельный вес жидкости;
Δx, Δy, Δz — объем кубика.

Сократив полученные равенства, найдем, что

Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’_z и P»_z, можно пренебречь и тогда окончательно

Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е.

Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила — сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

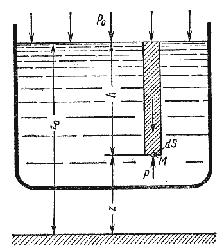
Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

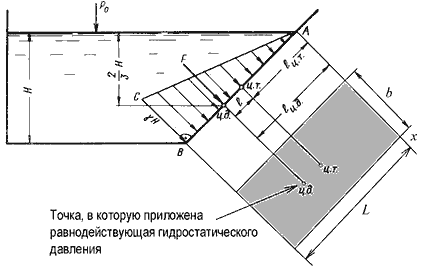
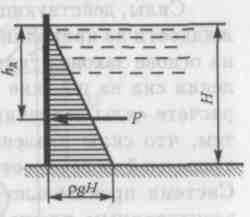
Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Избыточное гидростатическое давление в точке А будет равно

Соответственно давление в точке В:

где H — глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

где hc = Н/2 — глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

где J_Аx — момент инерции площади S относительно центральной оси, параллельной Аx.

В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

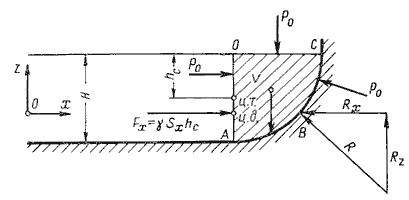
Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскость yOz.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

Теперь спроецируем все силы на ось Оz:

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что

Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

Для однородного тела плавающего на поверхности справедливо соотношение

где: V — объем плавающего тела;
ρ_m — плотность тела.

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

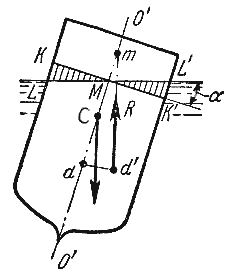
Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O’-O», представляющей ось симметрии судна и называемой осью плавания (рис.2.5).

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O’-O». Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным — в противном случае.

Теперь рассмотрим условия равновесия судна:

1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h&lt0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим два примера такого относительного покоя.

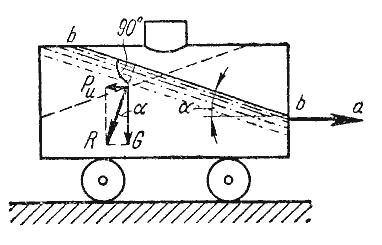
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).

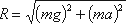
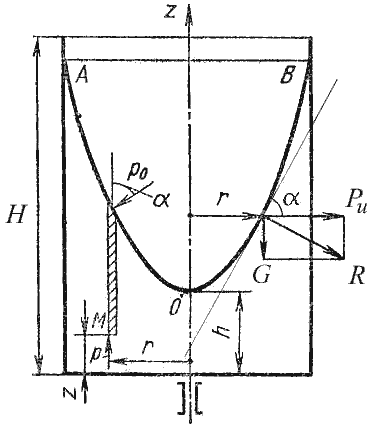
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции P_u, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен

Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).

В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила P_u = mω 2 r, где r — расстояние частицы от оси вращения, а ω — угловая скорость вращения сосуда.

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим

С другой стороны:

где z — координата рассматриваемой точки. Таким образом, получаем:

Силы давления на плоские и криволинейные поверхности

Дифференциальное уравнение равновесия жидкости (уравнения Эйлера)

Система уравнений Эйлера (уравнения равновесия) определяет закон распределения давления в покоящейся жидкости вдоль соответствующей оси координат.

здесь X,Y,Z – напряжения массовых сил в проекциях на соответствующие оси координат x, y, z,

p – давление в соответствующей точке жидкости,

ρ — плотность жидкости.

Из уравнений Эйлера можно получить следующий вид основного дифференциального уравнения равновесия жидкости

Если ввести силовую (потенциальную) функцию U, такую, что

то для несжимаемой жидкости дифференциальное уравнение равновесия примет вид:

Основное уравнение гидростатики

В однородном поле силы тяжести при постоянстве плотности жидкости

dU=gdz,

dp= – ρgdz,

Проинтегрировав, получим основное уравнение гидростатики:

p=p0+ρgh,

h=(z0-z) — расстояние по вертикали между рассматриваемыми двумя точками (нулевой и точкой, в которой определяется давление)

Основным законом (уравнением) гидростатики называется уравнение:

р— гидростатическое давление (абсолютное или избыточное) в произвольной точке жидкости,

— плотность жидкости,

g — ускорение свободного падения,

z— высота точки над плоскостью сравнения (геометрический напор),

H— гидростатический напор.

Уравнение показывает, что гидростатический напор во всех точках покоящейся жидкости является постоянной величиной.

Иногда основным законом гидростатики называют принцип Паскаля.

Силы давления на плоские и криволинейные поверхности

Для определения силы давления жидкости на плоскую стенку, наклоненную к горизонту под углом α, используем основное уравнение гидростатики.

Расположим систему координат так, что стенка будет находиться в координатной плос-кости xOy, ось Oy пройдет вдоль стенки, начало координат О поместим в точку пересечения свободной поверхности и стенки (рис. 1.1). На схеме: dS — площадь элементарной площадки; h, z — глубина погружения и координата центра тяжести элементарной площадки; С — центр тяжести смоченной поверхности стенки; hC, yC — глубина погружения и координата центра тяжести смоченной поверхности стенки; р0 — давление на свободной поверхности; Р — сила давления на плоскую стенку; α — угол наклона стенки к горизонту.

Определим силу давления Р, действующую на стенку со стороны жидкости. Со строны жидкостина стенки действует сила, вызванная гидростатическим давлением. Для вычисления силы давления на стенку на ней выделяют элементарную площадку dS, малые размеры которой позволяют считать ее плоской, давление — равномерно распределенным по площадке. В таком случае силу давления dP на элементарную площадку dS определяет соотношение:

dP=(p0+ρgh)dS,

где р0 — давление на свободной поверхности; h — глубина погружения центра площадки, измеренная вдоль оси y от свободной поверхности. Заменяя h=y∙sinα для силы давления на площадку dS, будем иметь выражение

dP=(p0+ρgy∙sinα)dS,

а сила давления, действующая на плоскую стенку площадью, вычисляется интегрированием по площади стенки, соприкасающейся с жидкостью

Интергал представляет собой статический момент смоченной площади стенки S относительно оси Оx. Он равен =yC∙S. Таким образом, выражение для силы давления, действющей со стороны жидкости на плоскую стенку приобретает вид:

Из полученного выражения можно видеть, что значение силы давления равно произве-дению давления в центре тяжести смоченной поверхности pC на площадь смоченной поверхности.

Результирующая сила давления на стенку — это разность сил давления на стенку с двух сторон. Если с одной стороны на стенку действует давление на свободную поверхность р0 и давление жидкости pgh, а с другой — атмосферное давление ра, то результирующая сила:

R = (po + ρghC)S−paS = (p0 + pghC−pa)S

представляет собой силу избыточного давления, т.е.

R = ризбC∙S

ризбC = p0 + ρghC−рa

является избыточным давлением в центре тяжести смоченной поверхности.

Точку D, в которой приложена сила P, называют центром давления. Так как внешнее давле-ние р0 передаетсявсем точкам площади S одинаково, то равно-действующая этого давления будет приложена в центре тяжести площади S. Для нахождения точки приложения силы избыточного давления жидкости (точка D) используем теорему Вариньона: сумма моментов составляющих сил относительно какой-либо оси равна моменту равнодействующей относительно той же оси

Предположим, что центр избыточного давления находится в точке D с координатой yD. Тогда момент равнодействующей силы избыточного давления относительно оси у

M = RyD = pghСSyD,

где hC — расстояние от центра тяжести смоченной поверхности до оси Oy.

Момент составляющих силы избыточного давления относительно той же оси

h = y∙sina,

представляет собой момент инерции рассматриваемой смоченной поверхности относительно оси x. Таким образом:

∑My=pgJxsinα

Из равенства выражений

pghCSyD = pgJx sinα

yD = Jx sinα/(hCS) = Jx/(yСS),

где yС — координата центра тяжести смоченной поверхности.

Выражая момент инерции Jx через центральный момент инерции смоченной поверхности JC:

Jx = JC + y2С S,

определим координату центра избыточного давления

Из полученной формулы видно, что центр давления не совпадает с центром тяжести смоченной поверхности стенки (расположен ниже него).

Если давление ро равно атмосферному и оно действует с обеих сторон стенки, то точка D и будет центром давления. Когда же р0 является повышенным, то центр давления находится по правилам механики как точка приложения равнодействующей двух сил: R и р0S. При этом, чем больше вторая сила по сравнению с первой, тем очевидно ближе центр давления к центру тяжести площади S.

Выше было дано определение лишь одной координаты центра давления—yD. Для определения другой его координаты — xD следует составить уравнение моментов относительно оси оу.

В том частном случае, когда стенка имеет прямоугольную форму, причем одна из сторон прямоугольника совпадает со свободной поверхностью жидкости, положение центра давления находится очень просто. Так как эпюра давления жидкости на стенку изображается прямоугольным треугольником (рис.1.2), центр тяжести которого находится на 1/3 высоты b треугольника, то и центр давления жидкости будет расположен на 1/3 b, считая снизу.

Силу давления и центр давления можно определить по эпюре давления. Построим эпюру давления на стенку (рис. 1.2), учитывая, что стенка имеет прямоугольную форму, причем одна из сторон совпадает со свободной поверхностью жидкости и что на свободной поверхности атмосферное давление ра, т.е. с одной стороны на стенку действует атмосферное давление и давление жидкости pgh, с другой — атмосферное давление.

Сила давления Р на стенку равна весу жидкости в объеме призмы:

P=Sэп a

где Sэп —площадь плоской эпюры; a — длина стенки.

В данном случае площадь эпюры — это площадь треугольника. Тогда сила давления на стенку

P = pgh∙b∙a/2,

где h — глубина жидкости; b — высота стенки.

Линия действия силы давления P будет проходить через центр тяжести пространственной эпюры давления и проектироваться на центр тяжести основания (в данном случае треугольника), который отстоит от вершины треугольника на 2/3 его высоты, т.е.

Определим силу давления и центр давления аналитически.

Сила избыточного давления равна

P = ризбС S = ρghC∙ba= ρgh∙b∙a/2,

где ризбС = ρghC =ρgh/2; S = b∙a.

Определим центр давления по формуле

Таким образом, результаты определения силы давления и центра давления по эпюре давления и аналитически совпадают.

В случае вертикальной стенки (рис.1.3а) эпюра распределения избыточного давления по высоте стенки имеет вид треугольника. Соответствующая этой эпюре сила давления на прямоугольную стенку равна

где b — ширина стенки.

Глубина hд погружения центра давления будет находиться в центре тяжести треугольника, который отстоит от вершины треугольника на 2/3 его высоты, или в соответствии с формулой

Как показывает формула , силы давления на горизонтальные стенки (днища сосудов), будут одинаковыми, если эти стенки имеют равные площади S и на них действуют одинаковые гидростатические давления. Форма сосуда не влияет на значение силы. На первый взгляд из-за различного количества одной и той же жидкости в показанных на рис. 1.3б сосудах силы давления на их днища будут разными. Такое неправильное суждение, противоречащее доказан-ному выше равенству сил давления, называют гидростатическим парадоксом.

Теперь определим силу давления на криволинейную поверхность АВ (рис.1.4а) при следу-ющих условиях. На свободную поверхность жидкости действует давление р0, которое больше ат-мосферного ра, а на поверхность АВ с одной строны действует полное гидростптическое давление р=р0+ρgh, а с другой стороны — атмосферное давление. Определить силу избыточного давления на цилиндрическую поверхностью.

Проекция силы давления на горизонтальную ось равна интегралу

где dPГ — проекция на горизонтальную ось элементарной силы dP, приложенной к выделенной на криволинейной стенке мощадке dS (рис. 1.4б) и равной

dP = (р0+ ρgh)dS

Здесь h — глубина погружения центра площадки, измеренная от свободной поверхности жидкости; ро — давление на этой поверхности. Обозначив через α угол наклона dP к горизонту, можно найти

dPГ = (ро + ρgh) cosαdS.

Произведение cosαdS соответствует проекции dSB элементарной площадки на вертикальную плоскость:

cosadS = dSB

dPГ = (р0 + pgh)dSB.

РГ = (р0 + ρghc) SВ

где hc — измеренная от свободной поверхности жидкости глубина погружения центра тяжести проекции криволинейной стенки на вертикальную плоскость; SB — площадь этой проекции.

Чтобы вычислить проекцию РВ на вертикальную ось, следует аналогичные операции выполнить с проекцией dPB элементарной силы давления. В этом случае

dPB = (p0 + pgh)dSГ,

где SГ — площадь проекции элементарной площадки на горизонтальную плоскость.

При интегрировании правой части этого уравнения получается два члена, первый из которых равен p0SГ, второй весу ρgV жидкости, занимающей объем 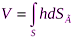между криволинейной поверхностью, свободным уровнем жидкости и вертикальными стенками 1,2,3:

Рв = р0SГ + ρgV

Объем V называют телом давления.

Полная сила гидростатического давления на криволинейную стенку составит

У стенок постоянной кривизны (цилиндрических, сферических) линия действия силы давления Р проходит через центр или ось кривизны. Точку приложения равнодействующей силы Р необходимо определять с помощью уравнения моментов.

Приведем другой вариант определения силы давления жидкости на криволинейную стенку.

Возьмем цилиндрическую поверхность АВ с образующей, перпендикулярной плоскости чертежа (рис.1.4), и рассмотрим определение силы давления жидкости на эту поверхность в двух случаях: а) жидкость расположена сверху (рис. 1.4б) и б) жидкость .расположена снизу (рис. 1.4в).

В случае «б» выделим объем жидкости, ограниченный рассматриваемой поверхностью АВ, вертикальными поверхностями, проведенными через границы этого участка, и свободной поверхностью жидкости, т. е. объем ABCD, и рассмотрим условия его равновесия в вертикальном и горизонтальном направлениях. Если. жидкость действует на поверхность АВ с силой Р, то поверхность АВ оказывает на жидкость такое же усилие Р, но направленное в обратную сторону. На рис. 1.4б показана эта сила реакции, разложенная на две составляющие: горизонтальную РГ, и вертикальную РВ.

Условие равновесия объема ABCD жидкости в вертикальном направлении имеет вид:

PB = p0SГ + G

где р0—давление на свободной поверхности жидкости;

SГ — площадь горизонтальной проекции поверхности АВ; G — вес выделенного объема жидкости, вес тела давления.

Условие равновесия того же объема жидкости в горизонтальном направлении запишем с учетом того, что силы давления жидкости на поверхности ЕС и AD взаимно уравновешиваются и остается лишь сила давления на площадь BE, т. е. на вертикальную проекцию поверхности АВ — SB. Будем иметь

PГ = SBρghc+paSb.

Определив вертикальную и горизонтальную составляющие полной силы давления Р, найдем эту последнюю:

В том случае, когда жидкость расположена снизу (случай «в», см. рис. 1.4), величина гидростатического давления во всех точках поверхности АВ будет иметь те же значения, что и в случае «б», но направление его будет противоположным, и суммарные силы РВ и РГ будут определяться теми же формулами, но с обратным знаком. При этом под величиной G следует понимать, так же как и в случае «б», вес жидкости в объеме ABCD, хотя этот объем и не заполнен жидкостью — вертикальная составляющая силы давления жидкости на твердую стенку направлена вверх. Положение центра давления на цилиндрической стенке легко может быть найдено, если силы РВ и РГ известны не только по величине, но и по направлению, т.е. если определены центр давления на вертикальной проекции стенки и центр тяжести выделенного объема ABCD. Задача значительно облегчается в том случае, когда рассматриваемая цилиндрическая поверхность является круговой, так как равнодействующая сила при этом пересекает ось поверхности. Это следует из того, что любая элементарная сила давления dP нормальна к поверхности, т. е, направлена по радиусу.

Изложенный способ определения силы давления на цилиндрические поверхности применим также и к сферическим поверхностям, причем равнодействующая сила в этом случае также проходит через центр поверхности и лежит в вертикальной плоскости симметрии.

Закон Архимеда

К рис. 1.6. r — радиус цилиндра; h — глубина погружения оси цилиндра; pg(h — r), pg(h + r) — давление на глубине h — r и h + r соответственно; Рг1 и Рг2 — горизонтальные составляющие силы давления на цилиндрическую поверхность; Рв1 и Рв2 — вертикальные составляющие силы давления на верхнюю и нижнюю части погруженного тела; Рв — вертикальная составляющая силы давления на погруженное тело.

Рассмотрим твердое тело, погруженное в покоящуюся жидкость (рис. 1.5). Оно находится в равновесии под действием двух сил, имеющих вертикальное направление: массовой силы G – веса тела, и поверхностной – результирующей силы давления жидкости P, окружающей тело. Результирующая сил давления в горизонтальном направлении равна нулю – силы давления, действующие на боковые поверхности справа и слева на тело, уравновешивают друг друга. Результирующую силу давления можно представить суммой двух составляющих P=Pверхн.+Pнижн

Составляющая Pверхн действует сверху на тело в направлении силы тяжести, погружая тело. Составляющая Pнижн действует на нижнюю поверхность тела, выталкивая его на поверхность, поскольку давления во всех точках нижней поверхности в соответствии с основным законом гидростатики больше давлений в точках верхней поверхности. Разность этих сил уравновешивается силой тяжести G тела: или . Если плотность тела равна плотности жидкости, то можно сформулировать условие равновесия тела как закон Архимеда: погруженное в покоящуюся жидкость тело испытывает со стороны жидкости вертикальное подъемное усилие, равное весу жидкости в объеме погруженного тела. Точка приложения результирующей силы давления, выталкивающей тело, называется центром давления.

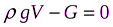
Закон Архимеда можно вывести и с точки зрения действия силы давления на криволинейную поверхность.

Определим силу давления жидкости на погруженное в нее тело (рис. 1.6), поверхность которого будем рассматривать как замкнутую криволинейную поверхность (например, цилиндр радиусом r, ось которого погружена на глубину h относительно пьезометрической плоскости).

Силу давления на данную криволинейную поверхность можно определить как геометрическую сумму вертикальной и горизонтальной составляющих.

Горизонтальная составляющая силы давления в рассматриваемом случае равна нулю, так как левая Рг1 и правая Рг2 составляющие численно равны и направлены в противоположные стороны:

Сила давления на поверхность погруженного тела равна вертикальной составляющей:

которая является результирующей двух сил:

Рв=Рв1+Рв2,

где Рв1 и Рв2 —- вертикальные составляющие, действующие соответственно на верхнюю и нижнюю части погруженного тела.

Определим разность сил Рв1 и Рв2. Рассечем погруженное тело горизонтальной плоскостью по диаметральной плоскости и построим тела давления на верхнюю и нижнюю части, а затем графически определим результирующее тело давления.

По рис. 1.6 видно, что результирующим телом давления является объем рассматриваемого цилиндра, и вертикальная составляющая силы давления равна весу жидкости в объеме, вытеснен-ном погруженным телом:

Рв=ρgV,

где V — объем тела.

Полученная формула выражает закон Архимеда: на погруженное в жидкость тело действует направленная вверх сила, численно равная весу вытесненной телом жидкости. Эта сила называется выталкивающей, или архимедовой, силой.

При выходе тела на свободную поверхность капельной жидкости выталкивающая сила уменьшается вследствие уменьшения объема погруженной части тела, и тело будет плавать на свободной поверхности. Условием плавания является выражение

G=ρgVП

где G — вес тела; VП— объем погруженной части тела.

С помощью этой формулы рассчитывается поплавковое устройство.

Подводное плавание тел. Рассмотрим остойчивость тела при подводном плавании. Тело будет плавать под водой, если сила тяжести тела под водой G равна силе Архимеда, т. е. G = Р. Тело будет тонуть, если G > Р и, наконец, тело всплывет,

если G G, то тело будет всплывать и часть тела при этом будет обсыхать. Тело будет всплывать до тех пор, пока сила Р не уменьшится настолько, что снова будет восстановлено равенство

P = G,

где Р равно весу жидкости в объеме погруженной части тела. Вес жидкости, вытесненный погруженной в нее частью тела, называется водоизмещением.

Плоскость сечения плавающего тела свободной поверхностью жидкости называется плос-костью плавания. Периметр плоскости плавания называется контуром плавания (ватерлинией).

При надводном плавании тело должно обладать остойчивостью, т. е. при малом крене (до 15—20°) тело должно возвращаться в первоначальное положение.

Тело обладает остойчивостью, если центр тяжести расположен ниже центра водоизмеще-ния. Но в плавающих судах это трудно бывает осуществить. Если центр тяжести расположен выше

центра водоизмещения, то плавающее над водой тело тоже может находиться в состоянии равновесия. В этом случае основное значение приобретает расположение точки М — метацентра. Метацентром называется точка пересечения оси плавания с линией действия силы Р (рис.1.9). Если метацентр расположен выше центра тяжести, то плавающее над водой тело остойчиво, так как возникающая при крене пара сил G — Р стремится возвратить его в состояние равновесия.

Расстояние вдоль оси плавания от центра тяжести тела до метацентра называется метацентрической высотой Нт. Метацентрическая высота положительна, если она от меряется вверх от центра тяжести. Если метацентрическая высота положительна, плавающее тело остойчиво.

Метацентрическая высота вычисляется по формуле:

Hm = I0 /V ± h = ρ±h

где I0—момент инерции площади ватерлинии (плоскости плавания) относительно продольной оси, проходящей через центр тяжести этой площади;

h — расстояние между центром тяжести тела и центром водоизмещения (рис.1.9);

ρ— метацентрический радиус.

На рис.1.9 показано остойчивое положение судна, а на рис. 1.10 — неостойчивое.

Закон Паскаля описывается формулой давления:

где р— это давление,

F — приложенная сила,

S — площадь сосуда.

Из формулы мы видим, что при увеличении силы воздействия при той же площади сосуда давление на его стенки будет увеличиваться. Измеряется давление в ньютонах на метр квадратный или в паскалях (Па), в честь учёного, открывшего закон, Паскаля.

На основе закона Паскаля работают различные гидравлические устройства: тормозные системы, гидравлические прессы и др.

Гидравлическая машина состоит из двух сообщающихся цилиндров разного диаметра, закрытых поршнями и заполненных жидкостью. Если на поршни действуют силы F1 и F2, то для равновесия системы необходимо, чтобы создаваемые этими силами давления были одинаковыми, так как согласно закону Паскаля давление передается жидкостью во все стороны одинаково. Следовательно, или

При равновесии силы, приложенные к поршням прямо пропорциональны площадям поршней. С помощью гидравлической машины можно малой силой уравновесить большую силу.

Гидродинамика — раздел гидравлики, в котором изучаются законы движения жидкости и ее взаимодействие с неподвижными и подвижными поверхностями.

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

Основные понятия о движении жидкости

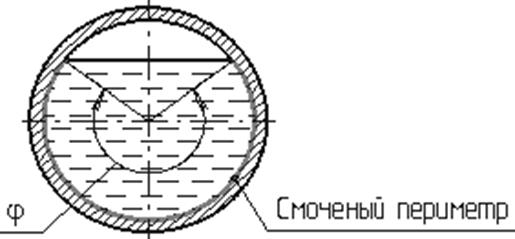
Живым сечением ω (м²) называют площадь поперечного сечения потока, перпендикулярную к направлению течения. Например, живое сечение трубы — круг (рис. 1.11, б); живое сечение клапана — кольцо с изменяющимся внутренним диаметром (рис. 1.11, б).

Рис. 1.11. Живые сечения: а — трубы, б – клапана

Смоченный периметр χ («хи») — часть периметра живого сечения, ограниченное твердыми стенками (рис. 1.12, выделен утолщенной линией).

Рис. 1.12. Смоченный периметр

Для круглой трубы

если угол в радианах, или

Расход потока Q — объем жидкости V, протекающей за единицу времени t через живое сечение ω.

Средняя скорость потока υ — скорость движения жидкости, определяющаяся отношением расхода жидкости Q к площади живого сечения ω

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Гидравлический радиус потока R — отношение живого сечения к смоченному периметру

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

υ = f(x, y, z)

P = φ f(x, y, z)

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

υ = f1(x, y, z, t)

P = φ f1(x, y, z, t)

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

Трубка тока — трубчатая поверхность, образуемая линиями тока с бесконечно малым поперечным сечением. Часть потока, заключенная внутри трубки тока называется элементарной струйкой.

Рис. 1.13. Линия тока и струйка

Течение жидкости может быть напорным и безнапорным. Напорное течение наблюдается в закрытых руслах без свободной поверхности. Напорное течение наблюдается в трубопроводах с повышенным (пониженным давлением). Безнапорное — течение со свободной поверхностью, которое наблюдается в открытых руслах (реки, открытые каналы, лотки и т.п.). В данном курсе будет рассматриваться только напорное течение.

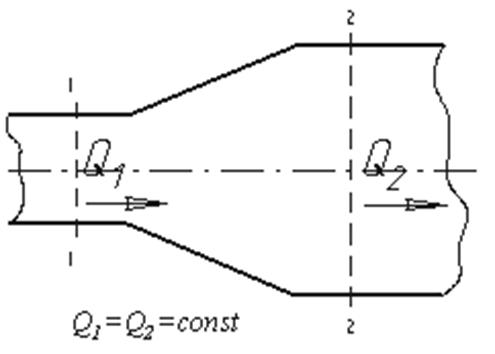
Рис. 1.14. Труба с переменным диаметром при постоянном расходе

Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q1=Q2= const, откуда

ω1υ1 = ω2υ2

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Сила давления жидкости на плоскую стенку

Сила давления жидкости на плоскую стенку равна произведению гидростатического давления р_с в центре тяжести площади стенки на площадь стенки S, т.е.

(2.6)

Центр давления(точка приложения силы F)расположен ниже центра тяжести площади или совпадает с последним в случае горизонтальной стенки.

Расстояние между центром тяжести площади и центром давления в направлении нормали к линии пересечения плоскости стенки со свободной поверхностью жидкости равно

(2.7)

где J₀ – момент инерции площади стенки относительно оси, проходящей через центр тяжести площади и параллельной линии пересечения плоскости стенки со свободной поверхностью;

у_с – координата центра тяжести площади.

Сила давления жидкости на криволинейную стенку, симметричную относительно вертикальной плоскости, складывается из горизонтальной F_Г и вертикальной F_В составляющих:

(2.8)

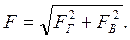
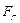
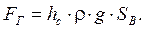
Горизонтальная составляющая равна силе давления жидкости на вертикальную проекцию данной стенки:

(2.9)

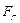
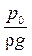
Вертикальная составляющая равна весу жидкости объеме V, заключенном между данной стенкой, свободной поверхностью жидкости и вертикальной проецирующей поверхностью, проведенной по контуру стенки. Если избыточное давление р₀ на свободной поверхности жидкости отлично от нуля, то при расчете следует эту поверхность мысленно поднять (или опустить) на высоту (пьезометрическую высоту) .

Относительный покой жидкости — это равновесие ее в движущихся сосудах, когда помимо силы тяжести на жидкость действует вторая массовая сила — сила инерции переносного движения, причем эта сила постоянна по времени.

Возможны два случая относительного покоя жидкости: в сосуде, движущемся прямолинейно и равноускоренно, и в сосуде, вращающемся вокруг вертикальной оси с постоянной угловой скоростью. В обоих случаях поверхности уровня, т.е. поверхности равного давления, и в том числе свободная поверхность жидкости, принимают такой вид, при котором равнодействующая массовая сила нормальна к этим поверхностям во всех их точках.

В сосуде, движущемся прямолинейно и равноускоренно, поверхности уровня будут плоскими.

В сосуде, равномерно вращающемся вокруг вертикальной оси, поверхности уровня представляют собой параболоиды вращения, ось которых совпадает с осью вращения сосуда.

Уравнение поверхности уровня (в частности, поверхности жидкости в открытом сосуде) в цилиндрических координатах (r, z) имеет вид

(2.10)

где z₀ – вертикальная координата вершины параболоида поверхности уровня;

r, z – координаты любой точки поверхности уровня.

Закон распределения давления по объему жидкости, вращающейся вместе с сосудом, выражается уравнением

(2.11)

где р₀ – давление в точке с координатами r = 0, z = z₀.

Таким образом, повышение давления в жидкости, возникающее вследствие ее вращения, равно

(2.12)

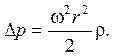
Примеры решения задач

Рис.2.8.

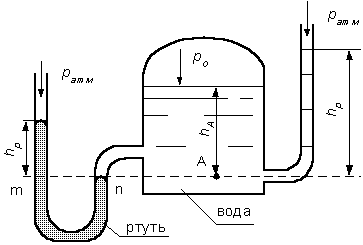
Пример 1. Определить абсолютное и избыточное гидростатическое давление
в точке А (рис. 2.8), расположенной в воде на глубине , и пьезометрическую высоту для точки А, если абсолютное гидростатическое давление на поверхности .

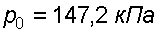
Согласно основного уравнения гидростатики абсолютное гидростатическое давление в точке А определится:

.

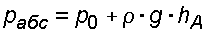
Избыточное давление в точке А равно:

Пьезометрическая высота для точки А равна:

Можно отметить, что пьезометром удобно измерять только относительно малые давления, в противном случае требуется большая высота пьезометра, что неудобно в эксплуатации.

Определить эти же величины U – образным манометром, заполненным ртутью. По поверхности раздела ртути и воды давления со стороны резервуара и открытого конца манометра будут одинаковы:

Следовательно, избыточное давление в точке А уравновешивается весом столба ртути высотой 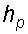над поверхностью раздела :

Находим высоту ртутного столба :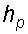

,

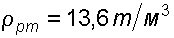
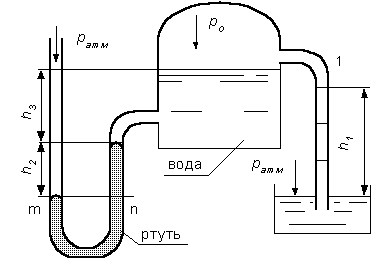
где – плотность ртути.

Рис.2.9.

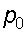
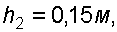
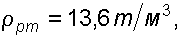
Пример 2. Определить давление в резервуаре (рис. 2.9) и высоту подъема уровня в трубке 1, если показания ртутного манометра .

Запишем условия равновесия для ртутного манометра для плоскости

а) со стороны резервуара

б) со стороны манометра ,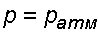

тогда

Таким образом, в резервуаре – вакуум, величина которого равна:

Условия равновесия трубки 1

Пример 3.

Рис.2.10.

Определить манометрическое давление в трубопроводе А (рис. 2.10),

если высота столба ртути по пьезометру 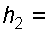25 см. Центр трубопровода расположен на 40 см ниже линии раздела между водой и ртутью.

Решение: Находим давление в точке В. Точка В расположена выше точки А на величину , следовательно, давление в точке В будет равно

.

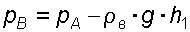
В точке С давление будет такое же, как в точке В, то есть

.

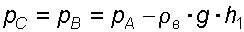
Определим давление в точке C, подходя, справа

.

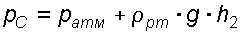
Приравнивая оба уравнения, получаем

.

Отсюда манометрическое давление

.

Пример 4.

Рис.2.11.

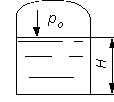
Определить все виды гидростатического давления в баке с нефтью на глубине (рис. 2.11), если давление на свободной поверхности нефти . Плотность нефти .

Решение: 1. Абсолютное гидростатическое давление у дна

2. Избыточное (манометрическое) давление у дна

3. Избыточное давление создаваемое столбом жидкости

4. Избыточное давление на свободной поверхности

Пример 5. Определить избыточное давление воды в трубе по показаниям батарейного ртутного манометра (рис. 2.12).

Рис.2.12.

Отметки уровней ртути от оси трубы: Плотность ртути , плотность
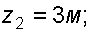
воды .

Решение: Батарейный ртутный манометр состоит из двух последовательно соединенных ртутных манометров. Давление воды в трубе уравновешивается перепадами уровней ртути, а так же перепадами уровней воды в трубках манометра. Суммируя, показания манометра от открытого конца до присоединения его к трубе получим: