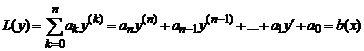Уравнение со специальной правой частью это

Уравнения с правой частью специального вида

Общее решение y_ОН линейного неоднородного дифференциального уравнения L(y)=b(x) есть сумма общего решения y_ОО соответствующего однородного уравнения L(y) = 0 и какого — либо частного решения y_ЧН исходного неоднородного уравнения. Для уравнений с постоянными коэффициентами и правой частью специального вида это частное решение может быть найдено достаточно просто.

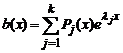
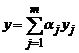
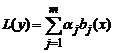
Функцию , где P_j(x) — некоторые полиномы (многочлены), назовём квазиполиномом. По теореме о наложении решений, если y_j , j=1,2. m — решения уравнений L(y) = b_j(x), то есть решение уравнения . Поэтому, не умаляя общности, будем считать, что правая часть уравнения L(y) = b(x) с постоянными коэффициентами имеет вид b(x) = P(x)e λx . В частности, если λ=α+βi — комплексное число, то наиболее общей правой частью указанного типа является функция

(1)

у которой P(x)и Q(x)- некоторые полиномы. Справедлив следующий результат.

Теорема. Линейное дифференциальное уравнение

с постоянными коэффициентами и правой частью вида (1) имеет частное решение

,

где k — кратность корня α+βi характеристического полинома соответствующего однородного уравнения, R(x) , S(x) — полиномы, подлежащие определению, степень которых равна максимальной степени полиномов P(x) , Q(x).

7.1. Уравнения с правой частью специального вида

Рассмотрим неоднородное линейное дифференциальное уравнение с постоянными коэффициентами

, (7.1)

Где , , …, , – вещественные числа.

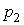
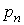
Уравнение (7.1) можно проинтегрировать рассмотренным ранее методом вариации произвольных постоянных, который сводится к составлению и решению системы линейных уравнений относительно функций, а также к интегрированию этих функций. Таких трудоемких операций можно избежать в некоторых случаях благодаря особому виду уравнения (7.1).

Поскольку общее решение соответствующего однородного уравнения (5.1) мы уже умеем находить, то получение общего решения уравнения (7.1) в силу теоремы подраздела 6.2 сводится к нахождению какого-нибудь частного его решения. Оказывается, что эта задача решается весьма просто при некоторых специальных видах функции 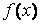в правой части уравнения (7.1). Далее рассматриваются следующие случаи.

1. Уравнения с правой частью в виде полинома.

В этом случае правая часть уравнения (7.1) представима в виде

,

Где – многочлен степени с известными коэффициентами.

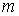
2. Правая часть в виде произведения полинома и экспоненты.

В данном случае правая часть уравнения (7.1) имеет вид

,

Где – многочлен степени с известными коэффициентами, – некоторое число.

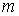
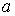
3. Правая часть в виде произведения полинома, экспоненты и гармонической функции.

В этом случае правая часть уравнения (7.1) имеет один из видов:

, ,

,

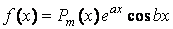
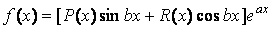
Где – многочлен степени с известными коэффициентами, и – многочлены известных степеней с известными коэффициентами, и – некоторые числа.

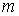
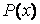
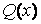
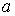
Для всех этих случаев на основании значений корней характеристического многочлена уравнения (7.1) и вида его правой части можно записать частное решение с точностью до коэффициентов входящих в него многочленов. Значения этих коэффициентов находятся путем составления и решения системы линейных алгебраических уравнений. Такой метод нахождения частного решения уравнения (7.1) называется Методом неопределенных коэффициентов.

Уравнение со специальной правой частью это

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид полинома от x степени m

Для уравнения с постоянными коэффициентами в случае, когда правая часть имеет специальный вид, удается найти частное решение методом неопределенных коэффициентов (методом подбора частных решений).

Рассмотрим этот метод для уравнения n-го порядка вида

где a₁, …, a_n — действительные числа, α — действительное число, P_m (x) — полином от x степени m, которая может быть равной нулю, так что этот полином может вырождаться в число, отличное от нуля.

Метод неопределенных коэффициентов состоит в том, что задается вид частного решения с неопределенными коэффициентами, которые определяются подстановкой в данное уравнение. Вид частного решения уравнения зависит от того, совпадает ли число α с корнями характеристического уравнения:

Если α не является корнем характеристического уравнения, то частное решение имеет вид

где Q_m (x) — полином степени m с коэффициентами, подлежащими определению.

Если α является корнем характеристического уравнения кратности k, то

т. е. частное решение приобретает множитель x k .

Случай для линейного неоднородного дифференциального уравнения с постоянными коэффициентами и с правой частью имеющей вид:

где α и b — действительные числа, P₁ и P₂ — полиномы от x, старшая степень которых равна m, так что один из них обязательно имеет степень m, а степень другого не превосходит m, и он может быть даже тождественно равен нулю.

Составим комплексное число α + ib, где действительная часть α есть коэффициент показателя множителя e αx , а мнимая часть b — коэффициент аргумента bx функций cos bx и sin bx.

Укажем вид частного решения уравнения (14.2) в двух случаях:

Если число α + ib не является корнем характеристического уравнения, то

где Q₁ и Q₂ — полиномы степени m с неопределенными коэффициентами; причем надо брать оба эти полинома даже в том случае, когда один из полиномов P₁ и P₂ тождественно равен нулю.

Если число α + ib есть корень характеристического уравнения кратности k, то

т. е. частное решение приобретает множитель x k .

ПРИМЕР 15.2. Найти общее решение уравнения
y′′ − 2y′ + y = 8e3x .
РЕШЕНИЕ. Сначала рассмотрим соответствующее однородное уравнение
y′′ − 2y′ + y = 0.
Так как его характеристическое уравнение λ2 − 2λ +1 = 0 имеет корни
λ1,2 =1, то общее решение однородного уравнения будет иметь вид
y C ex C xex = 1 + 2 .
Теперь найдем частное решение неоднородного уравнения. Правая
часть является произведением числа и показательной функции e3x :

f (x) = 8e3x ⇒ α = 3, β = 0, s = 0.
При этом число α ±βi = 3 не является корнем характеристического урав-
нения. Поэтому частное решение y

неоднородного уравнения надо искать
в виде

y = Ae3x ,
где A – неизвестный коэффициент.
Имеем:

y′′ = 9Ae3x .
Подставим

y′′ в неоднородное уравнение и получим
9Ae3x − 2⋅3Ae3x + Ae3x = 8e3x ,
⇒ 4Ae3x = 8e3x ,
⇒ 4A = 8 или A = 2.
Таким образом,

y = 2e3x – частное решение неоднородного уравне-
ния, а его общее решение имеет вид
( 1 2 )
y = C ex + C xex + 2e3x .