Уравнение колебаний маятника
Рис.1
Исследуем выражение (2) в зависимости от разности фаз (φ2 — φ1):
1) φ2 — φ1 = ±2mπ (m = 0, 1, 2, . ), тогда A=A1+A2, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний;
2) φ2 — φ1 = ±(2m+1)π (m = 0, 1, 2, . ), тогда A=|A1–A2|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний.
Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями.
Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω
23 Колебания физического маятника.
Физический маятник — осциллятор, представляющий собой твёрдое тело, совершающее колебания в поле каких-либо сил относительно точки, не являющейся центром масс этого тела, или неподвижной оси, перпендикулярной направлению действия сил и не проходящей через центр масс этого тела.
Определения
— угол отклонения маятника от равновесия;
— начальный угол отклонения маятника;
— масса маятника;
— расстояние от точки подвеса до центра тяжести маятника;
— радиус инерции относительно оси, проходящей через центр тяжести.
— ускорение свободного падения.
Момент инерции относительно оси, проходящей через точку подвеса:

[править] Дифференциальное уравнение движения физического маятника
Основная статья: Приведённая длина
Пренебрегая сопротивлением среды, дифференциальное уравнение колебаний физического маятника в поле силы тяжести записывается следующим образом:
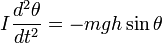
Полагая 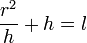
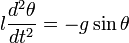
Последнее уравнение аналогично уравнению колебаний математического маятника длиной 

[править] Центр качания физического маятника
Центр качания — точка, в которой надо сосредоточить всю массу физического маятника, чтобы его период колебаний не изменился.
Поместим на луче, проходящем от точки подвеса через центр тяжести точку на расстоянии 
Действительно, если всю массу сосредоточить в центре качания, то центр качания будет совпадать с центром масс. Тогда момент инерции относительно оси подвеса будет равен 
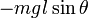
[править] Теорема Гюйгенса
[править] Формулировка
Если физический маятник подвесить за центр качания, то его период колебаний не изменится, а прежняя точка подвеса сделается новым центром качания.
[править] Доказательство
Вычислим приведенную длину для нового маятника:
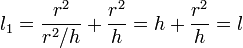
Совпадение приведённых длин для двух случаев и доказывает утверждение, сделанное в теореме.
[править] Период колебаний физического маятника
Для того, чтобы найти период колебаний физического маятника, необходимо решить уравнение качания. Для этого умножим левую часть этого уравнения на 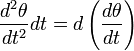
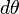
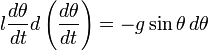
Интегрируя это уравнение, получаем.
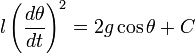
где 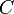
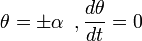
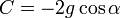
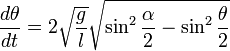
Отделяем переменные и интегрируем это уравнение:
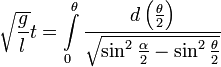
Удобно сделать замену переменной, полагая 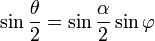
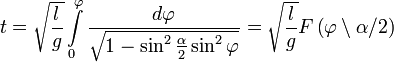
Здесь 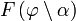
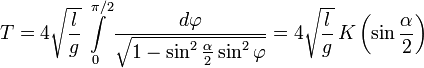
Здесь 
[править] Период малых колебаний физического маятника
Если амплитуда колебаний 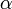
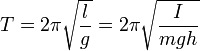
24 Колебания математического маятника
Математи́ческий ма́ятник — осциллятор, представляющий собой механическую систему, состоящую из материальной точки, находящейся на невесомой нерастяжимой нити или на невесомом стержне в однородном поле сил тяготения. Период малых собственных колебаний математического маятника длины l неподвижно подвешенного в однородном поле тяжести с ускорением свободного падения g равен
и не зависит [1] от амплитуды и массы маятника.
Плоский математический маятник со стержнем — система с одной степенью свободы. Если же стержень заменить на растяжимую нить, то это система с двумя степенями свободы со связью. Пример школьной задачи, в которой важен переход от одной к двум степеням свободы.
При малых колебаниях физический маятник колеблется так же, как математический с приведённой длиной.
Уравнение колебаний маятника
Колебания математического маятника описываются обыкновенным дифференциальным уравнением вида
где ω ― положительная константа, определяемая исключительно из параметров маятника. Неизвестная функция x(t) ― это угол отклонения маятника в момент t от нижнего положения равновесия, выраженный в радианах; 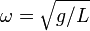
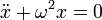
[править] Решения уравнения движения
[править] Гармонические колебания
Маятник, совершающий малые колебания, движется по синусоиде. Поскольку уравнение движения является обыкновенным ДУ второго порядка, для определения закона движения маятника необходимо задать два начальных условия — координату и скорость, из которых определяются две независимых константы:
где A — амплитуда колебаний маятника, θ0 — начальная фаза колебаний, ω — циклическая частота, которая определяется из уравнения движения. Движение, совершаемое маятником, называется гармоническими колебаниями
[править] Нелинейный маятник
Для маятника, совершающего колебания с большой амплитудой, закон движения более сложен:
где 

Параметр 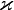
где 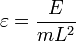
Период колебаний нелинейного маятника
где K — эллиптический интеграл первого рода.
[править] Движение по сепаратрисе
Движение маятника по сепаратрисе является непериодическим. В бесконечно далёкий момент времени он начинает падать из крайнего верхнего положения в какую-то сторону с нулевой скоростью, постепенно набирает её, и останавливается, возвратившись в исходное положение.
25 Затухающие колебания. Зависимость амплитуды от времени.
Затухающие колебания — колебания, энергия которых уменьшается с течением времени. Бесконечно длящийся процесс вида 
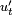
Пускай имеется система, состоящая из пружины (подчиняющейся закону Гука), один конец которой жёстко закреплён, а на другом находится тело массой m. Колебания совершаются в среде, где сила сопротивления пропорциональна скорости с коэффициентом c (см. вязкое трение).
Тогда второй закон Ньютона для рассматриваемой системы запишется так:
где Fc — сила сопротивления, Fy — сила упругости
или в дифференциальной форме
где k — коэффициент упругости в законе Гука, c — коэффициент сопротивления, устанавливающий соотношение между скоростью движения грузика и возникающей при этом силой сопротивления.
Для упрощения вводятся следующие обозначения:
Величину ω называют собственной частотой системы, ζ — коэффициентом затухания.
Тогда дифференциальное уравнение принимает вид
Сделав замену x = e λt , получают характеристическое уравнение
Корни которого вычисляются по следующей формуле
[править] Решения
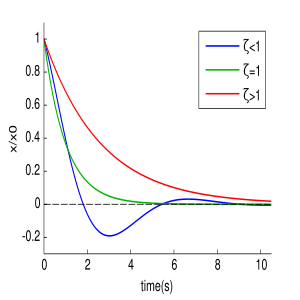
Зависимость графиков колебаний от значения ζ.
В зависимости от величины коэффициента затухания решение разделяется на три возможных варианта.
Если 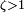
В этом случае колебания с самого начала экспоненциально затухают.
- Граница апериодичности
Если 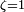
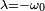
В данном случае может иметь место вре́менный рост, но потом — экспоненциальное затухание.
Если 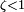
Тогда решением исходного дифференциального уравнения является
Где 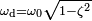
Константы c1 и c2 в каждом из случаев определяются из начальных условий:
26 Вынужденные колебания. Понятие резонанса.
Вынужденные колебания — колебания, происходящие под воздействием внешних сил, меняющихся во времени.
Автоколебания отличаются от вынужденных колебаний тем, что последние вызваны периодическим внешним воздействием и происходят с частотой этого воздействия, в то время как возникновение автоколебаний и их частота определяются внутренними свойствами самой автоколебательной системы.
Наиболее простой и содержательный пример вынужденных колебаний можно получить из рассмотрения гармонического осциллятора и вынуждающей силы, которая изменяется по закону: 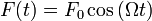
Уравнение собственных колебаний физического маятника
Общие понятия теории собственных колебаний.
Собственными называются колебания, которые совершает система около положения устойчивого равновесия после первоначального возмущения под действием только внутренних сил.
Какая сила должна действовать на систему, чтобы колебания были гармоническими? Так как для гармонических колебаний уравнение, связывающее ускорение и координату материальной точки выглядят как
то согласно II закону Ньютона справедливо следующее равенство:
F = m·a = — m·w 2 ·х = — k·x , (10.1)
где k — постоянная величина.
Итак, тело совершает гармонические колебания, если сила, возвращающая его в положение равновесия, пропорциональна смещению и направлена в противоположную этому смещению сторону.
Такая сила называется квазиупругой.
На практике зависимость F(x) является более сложной. Однако, при малых значениях величины х эту функцию можно разложить в ряд:
и пренебречь слагаемыми более высокого, чем 1 порядка малости. Следовательно, любая система с одной степенью свободы при достаточно малом отклонении от положения равновесия будет гармонически колебаться.
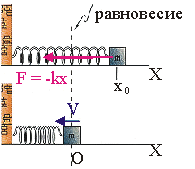
Рис. 10.1.
Уравнение динамики собственных колебаний. Рассмотрим колебания груза на пружине, считая, что вся масса сосредоточена в грузе, а упругость — в пружине. При х = 0 пружина не деформирована (см. рис. 10.1). Предположим, что сила трения в системе отсутствует Fтр = 0. В случае смещения тела от положения равновесия возникает сила упругости, действующая на тело и стремящаяся возвратить его в положение равновесия. Поскольку при малых деформациях х эта сила равна F = — k·x , то уравнение динамики движения груза согласно II закону Ньютона можно записать в виде:
Поскольку ускорение — есть вторая производная от координаты по времени, то решив дифференциальное уравнение (10.2), найдем зависимость x(t) . В теории дифференциальных уравнений показано, что общим решением уравнений типа x» + w0 2 ·x = 0 выражается зависимостью вида: x = A·cos(w0·t + f 0 ) .
Можно рассуждать также следующим образом. Из (10.2) имеем, что для гармонических колебаний a = — w0 2 ·x , т.е. ускорение а пропорционально х и направлено в противоположную к нему сторону. Следовательно, колебания груза в случае выполнения условия (10.2) являются гармоническими и описываются уравнением:
x = A·cos(w0·t + f 0 ) , (10.3)
где w0 = (k/m) 1/2 — собственная частота колебаний.
Значение w0 зависит только от физических свойств системы и не зависит от начальных условий.
Расчет параметров собственных колебаний. Амплитуда A и начальная фаза f 0 , называемые параметрами колебаний, не зависят от свойств системы, а определяются только начальными условиями, т.е. значением смещения и скорости в начальный момент времени:
Задав x0 и u 0 , получим два уравнения для расчета амплитуды и начальной фазы:
Уравнения (10.4) и (10.5) задают значения A и f 0 .
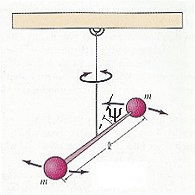
Рис. 10.2. Крутильные колебания.
Примеры собственных колебаний .
Крутильные колебания (см. рис. 10.2). Пусть y — угловая координата, I — момент инерции, K — модуль кручения. Уравнение динамики крутильных колебаний имеет вид:
I· e = — K· y или
y » = — K· y /I . (10.6)
Сравнивая уравнения (10.6) и (10.1), видим, что они аналогичны. Следовательно, решение уравнения (10.6) имеет вид гармонической функции:
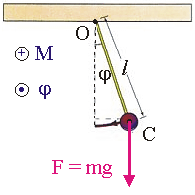
Рис. 10.3. Колебания физического маятника.
Физический маятник (см. рис. 10.3). Физическим маятником называется система, способная совершать колебания около положения равновесия, при этом массу системы нельзя считать сосредоточенной в одной точке. Введем обозначения: O — точка вращения; С — положение центра масс маятника; l — его длина; j — угол отклонения от положения равновесия. Уравнение динамики вращательного движения для физического маятника в проекции на ось вращения в случае его малых колебаний запишем в виде:
Решение этого уравнения имеет следующий вид:
Для математического маятника момент инерции и значение собственной частоты колебаний будут равны:
Собственную частоту физического маятника можно представить в виде, аналогичном выражению для математического маятника:
w 0 = (g/lприв) 1/2 ,
где lприв = I/(m·l) — приведенная длина маятника.
Собственные затухающие колебания. Логарифмический декремент затухания.

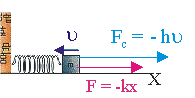
Рис. 10.4.
Уравнение динамики затухающих колебаний. В реальных случаях на тело, совершающее собственные гармонические колебания, действует сила трения. Наиболее распространен случай жидкого трения, когда сила трения (сопротивления среды) пропорциональна скорости:
Fтр = — h· u , (10.7)
где h — коэффициент сопротивления среды.
Уравнение (10.7) справедливо для малых скоростей. Согласно II закону Ньютона уравнение движения тела будет иметь вид:
После несложных преобразований получим:
x» + h/m·x’ + k/m·x = 0;
x» + 2· d ·x’ + w0 2 ·x = 0 . (10.8)
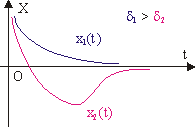
Рис. 10.6. Затухающие колебания в случае большого трения.
Решение уравнения динамики для случая большого и малого трения. Решение дифференциального уравнения (10.8) будет разным по характеру в зависимости от величины коэффициента сопротивления. При w 0 2 > d 2 , т.е. в случае малого сопротивления среды, тело совершает колебательное движение, а решение имеет вид:
Величины A0 и j0 , по-прежнему, определяются начальными условиями, а циклическая частота затухающих колебаний равна
и определяется характеристиками колеблющейся системы и окружающей среды. Таким образом, трение уменьшает частоту колебаний. Качественно этот факт можно объяснить так. Сила трения действует против скорости. Следовательно, для линейного осциллятора ее действие эквивалентно уменьшению возвращающей силы, т.е. упругости пружины. Это означает, что частота колебаний w уменьшается, а период Т увеличивается.
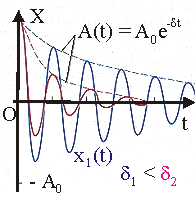
Рис. 10.5. Затухающие колебания.
График затухающего колебания представляет собой амплитудно-модулированную синусоиду (см. рис. 10.5). Модулирующая функция — экспонента равна:
Колебание в данном случае не является гармоническим и даже периодическим. Условно, периодом затухающего колебания называется минимальный промежуток времени между локальными максимумами или минимумами функции x(t) .
При большом трении тело колебаний как таковых не совершает (см. рис. 10.6, кривая x1(t) ). Решение будет иметь вид:
Возможен и промежуточный вариант, также характерный для больших значений коэффициента затухания (кривая x2(t) на рис. 10.6).

Коэффициент затухания. Коэффициент d , определяющий быстроту изменения амплитуды, называется коэффициентом затухания. Если промежуток времени D t = 1/ d , то А0/А = е . Отсюда вытекает физический смысл коэффициента затухания:
величина 1/ d , равна промежутку времени, по истечении которого амплитуда колебаний уменьшается в е = 2.73 раз.
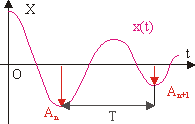
Рис. 10.7. К определению логарифмического декремента затухания.
Логарифмический декремент затухания, добротность. Коэффициент затухания d не дает полного представления об интенсивности затухания. Допустим, что для одного осциллятора колебания прекратились через 10 секунд, а для второго — через 100. Какой из осцилляторов обладает более быстрым затуханием? На этот вопрос ответить невозможно, если не учесть, сколько колебаний система успела совершить за это время.
Для характеристики интенсивности затухания вводят понятие логарифмического декремента затухания. Пусть Т — условный период затухающего колебания, Аn и An+1 — амплитудные значения функции x(t) для двух ее последовательных экстремумов (см. рис. 10.7). Величина d , равная:
называется логарифмическим декрементом затухания. Выясним связь между d и d :
d = ln( Аn /An+1) = ln(A0·e — d ·t /A0·e — d ·(T + t) ) =
= ln(e d ·T ) = d ·T = d . (10.13)
Используя уравнение (10.13), можно преобразовать закон изменения амплитуды:
An = A0·e — d ·t = A0·e — d ·T·t/T = A0·e -d·n , (10.14)
где n = t/T — число колебаний за время t .
Величина 1/d равна числу колебаний, за которое их амплитуда уменьшается в е раз.
Если значение d невелико ( d ), то можно показать, что
Логарифмический декремент связан с другой важной характеристикой колебаний — добротностью q следующим соотношением:

Динамика вынужденных колебаний. Резонанс.

Уравнение динамики колебаний, происходящих под действием гармонической силы. Вынужденными называются колебания, которые система совершает под действием внешней силы. Характер движения зависит от особенностей внешней силы. Она может быть любой периодически изменяющей свое значение. Наиболее важным является случай гармонической внешней силы. Более сложные случаи ее изменения во времени сводятся к этому простейшему.
Будем считать, что внешняя сила действует на линейный гармонический осциллятор по следующему закону:
Кроме внешней силы на осциллятор, по-прежнему, действуют квазиупругая сила и сила трения. Согласно II закону Ньютона уравнение движения имеет вид:
m·x» + h·x’ + k·x = F0· cos( w ·t)
или
x» + 2· d ·x’ + w0 2 ·x = F0· cos( w ·t)/m . (10.17)
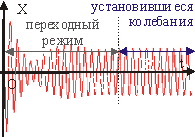
Рис. 10.8.
Уравнение вынужденных колебаний. Уравнение (10.17) — линейное неоднородное дифференциальное уравнение II порядка. В неоднородном уравнении, в отличии от однородного, существуют слагаемые, содержащие аргумент (в нашем случае переменную t ).
Решение неоднородного уравнения x(t) представляет сумму общего решения однородного уравнения x1(t) и частного решения неоднородного уравнения x2(t) , т.е. x(t) = x1(t) + x2(t) . Первое нам известно — это решение уравнения собственных затухающих колебаний, а второе, исходя из тригонометрических соображений, будем искать в виде:
х2(t) = A·cos( w ·t + f ) ,
где A и f — постоянные величины, представляющие собой амплитуду и сдвиг фаз между смещением и внешней силой.
Таким образом, общее решение будут иметь вид:
x(t) = A0·e — d ·t ·sin(w·t + j0 ) + A·cos( w ·t + f ) . (10.18)
Первое слагаемое правой части этого выражения описывает собственные затухающие колебания, зависящие от начальных условий. Из уравнения (10.18) следует, что в течение определенного промежутка времени осциллятор будет совершать сложное негармоническое движение, т.к. оно является результатом сложения двух асинхронных колебаний. Однако, через промежуток времени t
1/ d амплитуда и энергия собственных колебаний уменьшатся до нуля и они прекратятся. При этом второе слагаемое останется неизменным и результирующее колебание будет гармоническим (см. рис. 10.8, 10.9).

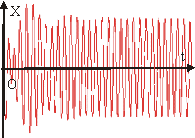
Рис. 10.9.
Переходной и установившийся режимы колебаний. Колебания, которые будут совершаться после затухания собственных колебаний, называются установившимися вынужденными колебаниями. Процесс установления этих колебаний называется переходным режимом (см. рис. 10.8).
Установившиеся колебания не зависят от начальных условий и описываются уравнением:
х = A·cos( w ·t + f ) . (10.19)
Частота вынужденных колебаний w равна частоте вынуждающей силы, а амплитуда A и сдвиг фаз f смещения относительно внешней силы зависят от значений собственной частоты колебаний w 0 , частоты вынуждающей силы w и коэффициента затухания d (см. рис. 10.8, 10.9).
Параметры вынужденных колебаний. Найдем величины А и f . Для этого подставим уравнение (10.19) и его производные по времени в выражение (10.17). Воспользовавшись методом векторных диаграмм, получим, что уравнение обращается в тождество только для определенных значений A и f .
A = (F0/m)/((w 0 2 — w 2 ) 2 + 4 d 2 · w 2 ) 1/2 . (10.20)
Амплитуда вынужденных колебаний пропорциональна амплитуде вынуждающей силы и существенно зависит от соотношения между частотой вынуждающей силы и собственной частотой.
Величину сдвига фаз между смещением и вынуждающей силой будет равна:
tg f = — 2 d · w /(w 0 2 — w 2 ) . (10.21)
Обратите внимание, что смещение отстает по фазе от вынуждающей силы.

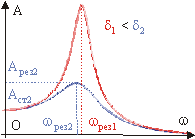
Рис. 10.10. Амплитудно-резонансная кривая.
Амплитудная резонансная кривая. Резонанс. Построим зависимость А( w ) , график которой называется амплитудной резонансной кривой. Вид этой кривой зависит от величины коэффициента затухания d (см. рис. 10.10). Амплитуда, соответствующая значению частоты w = 0, называется статическим смещением. Т.к. F0 = k·Aст , то
Из графика видно, что при определенном значении частоты вынуждающей силы амплитуда осциллятора становится максимальной.
Явление, при котором амплитуда колебаний системы достигает максимального значения, характерного для некоторого значении частоты вынуждающей силы называется резонансом.
Частота вынуждающей силы, при которой наступает данное явление, называется резонансной. Приравнивая к нулю производную по частоте выражения (10.20) и пренебрегая слагаемыми второго порядка малости, получим формулы для расчета резонансной частоты w рез и амплитуды Арез :
При значении d = 0 амплитуда колебаний в резонансе стремится к бесконечности.
Важной характеристикой осциллятора является отношение амплитуды его колебаний в резонансе к ее статическому значению. Из формул (10.21) и (10.23) следует, что это отношение равно добротности системы:
Арез/Аст = p /d = Q ,
где d — логарифмический декремент затухания.
Добротность является важнейшей характеристикой резонансных свойств системы.
Рассмотрим чему равен сдвиг фаз между смещением и силой при резонансе. Допустим, что при w = w 0 сила и смещение подчиняются следующим законам:
Тогда уравнение для скорости колеблющейся частицы (осциллятора) имеет вид:
x’ = u = — A· w ·cos( w 0 ·t) .
Из этих соотношений видно, что скорость u и сила колеблются в фазе. Следовательно, мощность, сообщаемая осциллятору внешней силой, равна N = F· u. Ее значение положительно в любой момент времени, следовательно, работа внешней силы достигает своего максимального значения. Энергия, передаваемая осциллятору внешней силой, в этом случае направлена на преодоление сил трения.
Примеры . Явление резонанса используется в работе резонансных контуров в электрических схемах, усиливающих полезный сигнал, наличие резонанса необходимо учитывать при расчете механических конструкций на прочность.
Изучение колебаний физического маятника, методические указания к лабораторной работе № 3
На правах рукописи
Министерство образования Российской Федерации
Волгоградская государственная архитектурно-строительная академия
ИЗУЧЕНИЕ КОЛЕБАНИЙ ФИЗИЧЕСКОГО МАЯТНИКА
Методические указания
Волгоград 2010
Методические указания к лабораторной работе № 3 по курсу физики «Изучение колебаний физического маятника» / Сост. ; ВолгГАСА.—Волгоград, 2002. – 8 с.
Для студентов всех специальностей.
Табл. 3. Библиогр. 3 назв.
© Волгоградская государственная архитектурно-строительная академия, 2002
Цель работы: Исследование зависимости периода колебаний физического маятника от его длины, определение момента инерции маятника и ускорения свободного падения.
Приборы и принадлежности: физический маятник в виде металлической линейки с отверстиями, секундомер.

Пусть маятник массой m и длиной l отклонен от положения равновесия на угол a. Движение физического маятника описывается основным законом динамики вращательного движения, который для абсолютно твердого тела имеет вид
 где М – момент внешних сил;
где М – момент внешних сил;
— угловое ускорение движения маятника, которое характеризует быстроту изменения угловой скорости по времени, и равно второй производной от угла поворота по времени;
J – момент инерции тела относительно оси вращения О.
Момент инерции маятника выразим, используя теорему Штейнера. Согласно данной теореме момент инерции твердого тела J относительно произвольной оси складывается из момента инерции Jс относительно параллельной оси, проходящей через центр инерции, и произведения массы тела на квадрат расстояния между осями
В нашем случае Jс – момент инерции относитльно оси, проходящей параллельно оси вращения через центр тяжести маятника С.
Момент внешних сил М складывается из момента силы тяжести и момента сил трения, которым в нашем рассмотрении можно пренебречь, т. е. считать, что Мтр=0. Момент силы тяжести равен произведению силы тяжести mg на расстояние от линии действия силы до оси вращения l sina (плечо силы, рис.1)
Знак минус показывает, что момент силы направлен противоположно углу отклонения маятника от положения равновесия, т. е является возвращающим моментом. Подставив (3) в (1), получим
Это уравнение, справедливое для любых значений амплитуды колебаний физического маятника, можно упростить для случая малых колебаний, когда угол отклонения маятника от положения равновесия мал и можно положить sina»a. Тогда уравнение движения маятника принимает вид
 (4)
(4)
Решение этого уравнения можно записать в виде
где ao – амплитуда колебаний (максимальное отклонение);
wo – собственная частота колебаний;
jo — начальная фаза колебаний.
Продифференцировав дважды уравнение (5) по времени и подставив в дифференциальное уравнение (4), получим соотношение
которое удовлетворяется при условии Jwo2- mgl=0. Отсюда собственная частота колебаний физического маятника
Тогда уравнение движения можно записать в виде дифференциального уравнения свободных гармонических колебаний

Амплитуда и начальная фаза колебаний определяются из начальных условий. Если в начальный момент времени t=0 известны угол отклонения маятника от положения равновесия a(0) и угловая скорость движения маятника da/dt=w(0) (не путать угловую скорость движения маятника w с собственной частотой колебаний wо!), имеем
a(0)=aosinjo и w(0)=woaocosjo.
Решая эту систему уравнений, получаем ao=(a2(0)+w2(0)/wo2)1/2 и jo=arctg(woa(0)/w(0)). Отсюда находим, что, если в начальный момент времени маятник покоится w(0)=0 в положении a=a(0), то амплитуда равна начальному отклонению маятника aо=a(0), а начальная фаза jо=p/2. Решение дифференциального уравнения для таких начальных условий имеет вид a(t)=ao sin (wot+p/2).

Если размеры тела малы по сравнению с длиной маятника l, то есть тело можно принять за материальную точку, подвешенную на невесомой нерастяжимой нити, то такой маятник является математическим маятником с периодом
Здесь учли, что момент инерции материальной точки относительно оси J=ml2. Как видим из сравнения (8) и (9), в отличие от математического маятника, период колебаний которого зависит только от длины и ускорения свободного падения, период колебаний физического маятника зависит также от его массы и момента инерции. Каждому физическому маятнику можно подобрать такой математический маятник, период колебаний которого равен периоду колебаний физического маятника. Длина такого математического маятника называется приведенной длиной физического маятника. Сопоставив (8) и (9) получим выражение для приведенной длины физического маятника
В отличие от математического маятника, зависимость периода колебаний которого от длины T
l1/2, для физического маятника, зависимость T(l) более сложная и представлена на рис.2.
Рис. 2. Зависимость периода колебаний физического маятника от длины.
Как следует из формулы (9), при l ® 0 период физического маятника
Т® ∞, то есть, если ось вращения проходит через центр инерции, то маятник находится в состоянии безразличного равновесия. При увеличении l ( когда выполняется условие ml2 >> Jc) период колебаний физического маятника стремится к периоду колебаний математического маятника. Зависимость Т(l) имеет минимум при некотором значении lmin.
Измеряя зависимость T(l) и построив график, можно определить момент инерции физического маятника Jc и ускорение свободного падения g. Для этого при Тмат> Т>Тmin находим два значения li и lk , соответствующие одному и тому же периоду Тi=Tk=T (рис. 2). Применив формулу (8) можно
записать
Решая совместно систему уравнений (11) и (12) относительно величин Jc и g , получим
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ
1. Подвесить физический маятник на седлообразную выемку опорной призмы отверстием, отстоящим от центра масс на величину l (см. табл. 3). Отклонить маятник на небольшой угол и отпустить. Измерить время 25 полных колебаний t¢. После этого подвесить маятник за симметричное отверстие, расположенное на таком же расстоянии от центра масс, и повторить измерение времени t¢¢. Найти среднее значение tср=(t¢+t¢¢)/2 и вычислить период колебаний T=tср/25. Результаты измерений занести в таблицу 1.
http://pipec8.narod.ru/fiz/coleb.htm
http://pandia.ru/text/78/034/23167.php
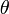 — угол отклонения маятника от равновесия;
— угол отклонения маятника от равновесия; — масса маятника;
— масса маятника;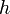 — расстояние от точки подвеса до центра тяжести маятника;
— расстояние от точки подвеса до центра тяжести маятника; — радиус инерции относительно оси, проходящей через центр тяжести.
— радиус инерции относительно оси, проходящей через центр тяжести.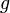 — ускорение свободного падения.
— ускорение свободного падения.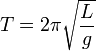

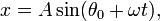
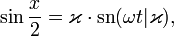
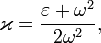


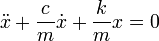
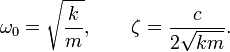
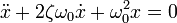

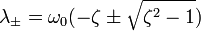

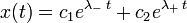

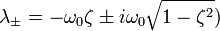
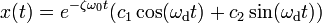
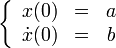




 где М – момент внешних сил;
где М – момент внешних сил;

 (4)
(4)



