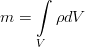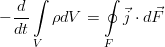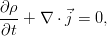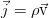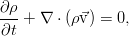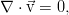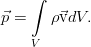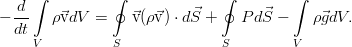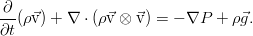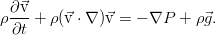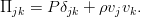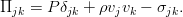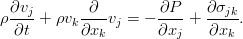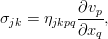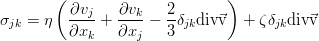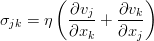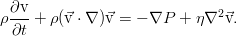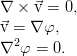Уравнение сохранения полной энергии сплошной среды

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

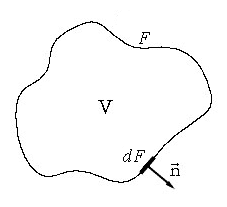
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

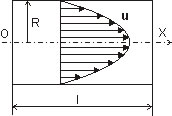
Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.

Механика сплошных сред (стр. 1 )

Из за большого объема этот материал размещен на нескольких страницах: 1 2 3 4 5 6

Уральский государственный технический университет

кафедра молекулярной физики

МЕХАНИКА СПЛОШНЫХ СРЕД

рАЗДЕЛ 2 — иДЕАЛЬНАЯ среда

7. Идеальная среда.. 68

7.1. Уравнения движения для сжимаемой и несжимаемой идеальной среды.. 68

7.1.1. Замкнутая система уравнений сохранения для идеальной среды.. 68

7.1.2. Движение несжимаемой среды.. 69

7.1.3. Изоэнтропическое движение. 70

7.1.4. Граничные и начальные условия. 71

7.2. Уравнение Бернулли. 72

7.2.1. Потенциальное движение идеальной среды.. 72

7.2.2. Линии тока и траектории. Трубка тока. 73

7.2.3. Скорость истечения идеальной несжимаемой жидкости из сосуда 75

7.2.4. Распределение давления в трубе переменного сечения. 75

7.2.5. Кавитация. 77

7.2.6. Трубка Пито. 78

7.3. Влияние сжимаемости среды.. 80

7.4. Вихревое движение. 83

7.4.1. Сохранение циркуляции скорости. Теорема Томсона. 83

7.4.2. Вихревая трубка. Теорема Гельмгольца. 84

7.4.3. Прямолинейная одиночная вихревая нить. 86

7.4.4. Примеры вихревых движений. 89

7.5. Потенциальное движение. 91

7.5.1. Потенциал скорости. Граничные условия. 91

7.5.2. Функция тока для плоского движения идеальной среды.. 93

7.5.3. Свойства функции тока. 93

7.6. Некоторые методы решения газодинамических задач для идеальной жидкости. 95

7.6.1. Метод конформных отображений. 95

7.6.2. Обтекание плоской пластинки идеальной несжимаемой жидкостью 95

7.6.3. Обтекание цилиндра идеальной несжимаемой жидкостью.. 97

7.6.4. Распределение давления на поверхности цилиндра. 99

Парадокс Даламбера. 99

7.7. Суперпозиция потенциальных потоков. 102

7.7.1. Обтекание бесконечного цилиндра с циркуляцией. 102

7.7.2. Распределение давления. Подъемная сила. 103

7.8. Графоаналитический метод. 107

7.9. Движение бесконечного цилиндра в идеальной несжимаемой среде. 109

7.9.1. Постановка задачи и методика решения. 109

7.9.2. Распределение давления около движущегося цилиндра. 111

7.9.3. Сила сопротивления движущегося шара. Присоединенная масса 113

7.10. Численные методы в механике сплошных идеальных сред.. 116

7.10.2. Краткая характеристика численных методов. 117

7.10.2.1. Метод конечных разностей. 117

7.10.2.2. Метод интегральных соотношений. 117

7.10.2.3. Метод характеристик. 118

7.10.2.4. Метод частиц в ячейках. 118

7.10.2.5. Метод конечных элементов. 119

7.10.2.6. Метод дискретных вихрей. 119

7.10.2.7. Статистические методы.. 120

7.10.3. Основы численных методов. 121

7.10.3.1. Задача интерполирования. 121

7.10.3.2. Интерполяционный многочлен Лагранжа. 121

7.10.3.3. Погрешность интерполирования. 122

7.10.4. Вычисление интегралов. 122

7.10.4.1. Квадратурные формулы Ньютона-Котеса. 122

7.10.4.2. Формула трапеций. 123

7.10.4.3. Формула Симпсона. 123

7.11. Применение метода потоков в механике сплошных идеальных сред.. 125

7.11.1. Общие замечания. 125

7.11.2. Описание метода потоков. 126

7.11.3. Конечно – разностные схемы метода потоков. 130

7.11.3.1. Постановка и решение задачи. 130

7.11.3.2. Обтекание прямоугольного выступа эйлеровым газом. 132

7.11.3.3. Этапы вычислительного цикла. 135

7.11.4. Результаты расчета. 137

7. Идеальная среда

Под жидкостью будем понимать как собственно саму жидкость, так и газ, полагая, что оба эти агрегатных состояния вещества представляют собой сплошную среду.

Идеальной жидкостью называют жидкость, у которой отсутствует вязкое трение и объёмная вязкость (h = 0, z = 0), теплопроводность (l = 0), а модуль сдвига равен 0 (m = 0). Несмотря на то, что это весьма идеализированная модель сплошной среды, многие характерные черты движения жидкостей могут быть изучены при помощи этой простейшей модели, по крайней мере, вдали от поверхности обтекаемых тел.

7.1. Уравнения движения для сжимаемой и несжимаемой идеальной среды

7.1.1. Замкнутая система уравнений сохранения для идеальной среды

В пренебрежении вязкостью для идеальной ньютоновской среды общий тензор напряжений согласно (6.11.2) имеет простой вид:

. (7.1.1)

Поэтому уравнение движения идеальной среды в соответствии с уравнением (6.4.9) можно записать в следующей форме:

(7.1.2)

Вообще говоря, можно было бы ослабить условие идеальности и полагать, что вязкость жидкости настолько мала, что . Однако это условие заведомо не выполняется вблизи поверхности обтекаемых тел.

Уравнение (7.1.2) называют уравнением Эйлера. Уравнение непрерывности движения (6.3.5), конечно, сохранит свой вид. Уравнение сохранения внутренней энергии согласно уравнению (6.7.7) и уравнению (6.7.1) можно записать в виде

, (7.1.3)

поскольку

Из второго уравнения системы – уравнения сохранения энтропии (6.7.10) следует физически очевидный результат:

, (7.1.4)

т. е. энтропия единицы массы индивидуальной частицы идеальной жидкости сохраняется в процессе движения. Этот результат очевиден, т. к. сделанные выше предположения лишили жидкость механизмов возрастания энтропии.

Таким образом, система уравнений сохранения для идеальной жидкости имеет вид:

(7.1.5)

Таким образом, имеется пять уравнений для нахождения семи неизвестных искомых функций (если внешние силы заданы): Для замыкания системы уравнений (7.1.5.) до полной необходимо добавить термическое уравнение состояния:

Внутренняя энергия eвн также может быть определена из калорического уравнения состояния:

7.1.2. Движение несжимаемой среды

Условием несжимаемости среды, как отмечалось ранее, является уравнение . В этом случае из уравнения непрерывности (6.3.3) следует, что dρ/dt =0, т. е. массовая плотность не зависит ни от координат физического пространства хi , ни от времени t. Тогда в уравнении Эйлера (7.1.2) плотность ρ можно внести под знак производной и уравнение записать в векторном виде

(7.1.6)

Для изоэнтропических движений несжимаемой среды уравнение (7.1.6) можно преобразовать к виду, содержащему только скорость. Для этого предположим, что внешние силы являются потенциальными, т. е. . Воспользуемся известной формулой из векторного анализа вида

(7.1.7)

После подстановки (7.1.7) в уравнение движения (7.1.6) получим:

(7.1.8)

Применив операцию rot к обеим частям уравнения (7.1.8) и учитывая, что rotѺ0, имеем:

(7.1.9)

Данное уравнение называют уравнением Эйлера в форме Громека. Это уравнение замечательно тем, что оно содержит только вектор скорости. Таким образом, в случае течений несжимаемых сред, если массовые силы являются потенциальными, скорости могут быть найдены независимо от других параметров течения.

При заданных краевых и начальных условиях решение уравнения (7.1.9) существует и оно единственное, т. е. задача становится чисто кинематической. Для отыскания других переменных характеристик течения необходимо, зная , вернуться к исходной форме уравнения движения Эйлера (7.1.6). Например, плотность может быть найдена из уравнения непрерывности, а — из уравнения движения Эйлера (7.1.6).

Если ввести аксиальный вектор w соотношением , то уравнение Громека можно записать в виде

. (7.1.10)

7.1.3. Изоэнтропическое движение

Уравнение сохранения энтропии (7.1.4) свидетельствует о том, что, если в начальный момент времени во всех точках объёма, занятого идеальной средой, энтропия была одинакова, то она останется той же самой во всех точках и во все последующие моменты времени. Тогда из уравнения (7.1.4) можно записать:

Движение жидкости с постоянным значением энтропии называют изоэнтропическим.

Используя условие изоэнтропичности движения (7.1.4), уравнению движения идеальной жидкости (7.1.2) можно придать другой вид. Для этого воспользуемся определением малого изменения энтальпии единицы массы и основным термодинамическим равенством (4.2.1) для замены малого изменения внутренней энергии в виде:

где — удельный объём жидкости.

Так как для изоэнтропического движения dS = 0, то имеем:

(7.1.11)

Эти соотношения означают, что при движении идеальной среды индивидуальная частица испытывает сжатие при увеличении давления. Тогда уравнение движения в системе уравнений сохранения (7.1.5) принимает вид:

(7.1.12)

7.1.4. Граничные и начальные условия

Поскольку идеальная среда не имеет вязкости, то её соседние слои могут иметь какие угодно скорости. Так, например, среда может двигаться вдоль обтекаемой твёрдой поверхности с любой скоростью. Поэтому единственным физическим ограничением для скорости среды, обтекающей некоторую твердую поверхность, есть условие не протекания или условие не накопления вещества на поверхности. Это условие ограничивает лишь нормальную к поверхности обтекаемого тела компоненту скорости среды. Так, на неподвижной поверхности нормальная компонента скорости жидкости должна быть равна нулю, а на поверхности, движущейся со скоростью u, нормальные компоненты скорости поверхности и жидкости должны быть равны, т. е.

(7.1.12)

В качестве начальных или, как уже было сказано выше, краевых условий необходимо задать все искомые функции в некоторый момент времени в рассматриваемой области движения или на её поверхности.

7.2. Уравнение Бернулли

7.2.1. Потенциальное движение идеальной среды

Движение жидкости, при котором во всем занятом движущейся жидкостью пространстве , называют потенциальным.

Рассмотрим в качестве массовой силы силу тяжести. Тогда, если ось z направлена в противоположную ускорению силы тяжести сторону, можно записать:

Тогда для стационарного () и потенциального () движения идеальной несжимаемой среды в поле тяжести из уравнения (7.1.8) следует

(7.2.1)

В любой точке потока последнее равенство может выполняться только тогда, когда выражение в скобках равно некоторой постоянной во всем поле течения среды, не зависящей от координат, т. е.

(7.2.2)

Уравнение (7.2.2) есть первый интеграл уравнения движения Эйлера (7.1.2), и его называют уравнением Бернулли для несжимаемой идеальной жидкости. Уравнение Бернулли по физическому смыслу является уравнением сохранения полной энергии единицы массы. Действительно, в нём слагаемые есть кинетическая энергия, потенциальная энергия и работа сил давления по изменению объема единицы массы, соответственно.

Для сжимаемой среды при изоэнтропическом движении массовая плотность не зависит от радиуса-вектора r и Поэтому в соответствии с (7.1.11) можно записать

.

Используя эту замену в (7.2.2), получаем уравнение Бернулли для несжимаемой жидкости при изоэнтропическом движении в форме

(7.2.3)

7.2.2. Линии тока и траектории. Трубка тока

Линия тока — это линия, касательная к которой в точке касания даёт направление скорости индивидуальной частицы. Траектория — это линия или кривая, описываемая индивидуальной частицей при своём движении. При установившемся движении линии тока и траектории совпадают. При неустановившемся движении это, вообще говоря, разные линии.

Для визуализации течения в экспериментах вводят в движущуюся жидкость мелкие, легкие частицы, которые при соответствующем освещении довольно ярко светятся. Если сфотографировать поле течения с небольшой выдержкой, то на фотографии можно наблюдать множество коротких черточек, «прочерчиваемых» за короткое время экспозиции на фотопластинке множеством светящихся частиц порошка. Можно подобрать к некоторому последовательному ряду чёрточек кривые, к которым эти чёрточки являются касательными, эти кривые и будут линиями тока в жидкости в данный момент времени. В другой момент времени неустановившегося движения линии тока могут быть другими. Если же значительно увеличить время экспозиции, то каждая частица «прочертит» на фотопластинке непрерывную линию через всё поле течения, охватываемое объективом. Эти линии и являются траекториями частиц жидкости.

Касательные к линии тока в различных её точках дают направление скорости различных индивидуальных частиц в данный момент времени. Касательные к траектории в различных её точках дают направление скорости одной и той же индивидуальной частицы в различные моменты времени.

Если в жидкости взять некоторый замкнутый контур и через все его точки провести линии тока, то они составят некоторую трубку, которую называют трубкой тока. Трубка тока замечательна тем, что по определению через её боковую поверхность нет потока жидкости. Жидкость в трубку тока может поступать только через её торцы. Элемент длины линии тока dr и скорость частицы u являются векторами коллинеарными, для которых отношение соответствующих компонент есть величина постоянная. Поэтому уравнение линии тока имеет вид

(7.2.4)

Рассмотрим стационарное (), не потенциальное (), изоэнтропическое () движение сжимаемой жидкости в поле потенциальных сил (). Спроектируем уравнение (7.1.9) на линию тока. Для этого умножим скалярно правую и левую часть уравнения (7.1.9) на единичный вектор l, касательный к линии тока:

l = l . Но векторное произведение в левой части данного уравнения представляет собой вектор, перпендикулярный вектору , а, следовательно, и l. Поэтому их скалярное произведение равно нулю. Тогда имеем:

l (7.2.5)

Здесь означает производную вдоль направления единичного вектора l. Следовательно, для данной линии тока справедливо уравнение Бернулли вида

(7.2.6)

Это уравнение является уравнением Бернулли для линии тока при стационарном, потенциальном движении идеальной сжимаемой жидкости в поле потенциальных сил тяжести. Уравнение (7.2.6) отличается от уравнения (7.2.2) только тем, что в случае не потенциального () движения жидкости в потенциальном поле силы тяжести константа в правой части уравнения (7.2.2) постоянна во всём поле течения жидкости. Тогда как в уравнении (7.2.6) константа в правой части является постоянной лишь для данной линии тока при не потенциальном движении, когда , в поле потенциальных сил тяжести и может иметь другое значение для другой линии тока. Для несжимаемой же жидкости при не потенциальном движении для линии тока уравнение Бернулли имеет вид:

(7.2.7)

Следует заметить, что возможно получить уравнение Бернулли в виде (7.2.7) каждый раз, когда удаётся выразить слагаемое (1/r) в виде градиента некоторой функции. Так, для изоэнтропического движения сжимаемой идеальной жидкости , а для несжимаемой идеальной жидкости Очевидно, что это можно сделать и при изотермическом движении, когда Тогда выражение можно выразить в виде градиента некоторой функции Ф(Р) в виде

Такие движения называются баротропными, а функцию Ф(P) называют баротропным потенциалом. Для баротропных движений уравнение Бернулли имеет вид

(7.2.8)

7.2.3. Скорость истечения идеальной несжимаемой жидкости из сосуда

Уравнение Бернулли имеет самое широкое применение на практике. Рассмотрим несколько примеров. В качестве первого примера рассмотрим стационарное истечение идеальной несжимаемой жидкости из сосуда (рис.7.1). Если полагать, что сосуд достаточно велик, а отверстие мало, то можно считать, что при истечении уровень жидкости не изменяется заметно в течение достаточно продолжительного промежутка времени. Пусть на поверхность жидкости в сосуде действует давление (например, атмосферное). Будем также полагать, что струя вытекает в пространство, где внешнее давление также равно (истечение в атмосферу). Обобщение на различные давления не составляет труда. Проведем некоторую гипотетическую линию тока и выберем на ней две точки: одну на поверхности жидкости в сосуде (точка 1), другую внутри отверстия (точка 2).

Тогда для этой линии тока можно записать уравнение Бернулли (7.2.7):

Поскольку поверхность жидкости в сосуде предполагается неподвижной ), из последнего равенства следует:

(7.2.9)

Заметим, что такую же скорость приобретает тело, которое падает в пустоте с высоты h.

7.2.4. Распределение давления в трубе переменного сечения

Рассмотрим стационарное движение идеальной несжимаемой жидкости в трубе переменного сечения, направленное слева направо на Рис.7.2. Действием силы тяжести можно пренебречь. Выберем какую — либо линию тока (например, осевую). На этой линии тока рассмотрим две произвольные точки 1 и 2. Тогда для этих точек на выбранной линии тока можно записать в

соответствии с уравнением Бернулли:

(7.2.10)

Из данного уравнения следует, что в той точке на линии тока, где скорость больше, гидростатическое давление меньше и наоборот. Непрерывность движения жидкости в трубе требует выполнения следующего закона:

(7.2.11)

Данный закон называют также условием не накопления вещества или

условием не разрывности струи в любом сечении трубы. В соответствии с этим законом поток массы при движении идеальной жидкости в трубе переменного сечения есть величина постоянная. Из этого условия следует, что скорость несжимаемой жидкости тем больше, чем меньше сечение трубы, и она максимальна в самом узком сечении трубы. Следовательно, в самом узком месте трубы давление минимально согласно (7.2.9). Если на поверхности трубы установить манометрические трубки, то жидкость в них будет находиться на разных уровнях. Самый низкий уровень манометрической жидкости, следовательно, будет в самом узком сечении трубы.

В качестве примеров, которые могут быть просто объяснены при помощи установленного вывода, можно привести следующие. Например, капитанам судов запрещается проводить сближение судов, идущих параллельным курсом, до некоторого минимального расстояния. Действительно, при этом вода между двумя судами приобретает некоторую дополнительную скорость за счёт сужения канала, образованного бортами судов, а давление воды между судами оказывается меньшим, чем вне них.

Поэтому возникают силы, равные разности сил давлений на внешние и внутренние борта судов и стремящиеся сблизить суда, что может привести к их столкновению (рис.7.3а). Хорошо известен экспериментальный факт, что, если продувать воздух между двумя параллельными листами бумаги, то они будут стремиться сблизиться (рис.7.3б).Действие пульверизатора также легко понять на основании полученного выше вывода. Если в отсутствие обдува жидкость в трубочке и флаконе была на одном уровне, то при продувании воздуха около верхнего торца трубочки давление атмосферного воздуха уменьшается, а внутри флакона атмосферное давление сохраняется, если имеется дополнительный канал в пробке. За счёт разности давлений жидкость выталкивается вверх по трубочке и разбрызгивается потоком воздуха (рис.7.3в).

При сильных и порывистых ветрах иногда наблюдается непривычное на первый взгляд явление. Крыша дома вместе с верхним венцом бревен поднимается вверх, а затем уже опрокидывается ветром. Нетрудно понять, почему это происходит. Если перед порывом ветра давление снаружи крыши и на чердаке дома уравниваются, то при резком порыве ветра над крышей создаётся меньшее давление, чем на чердаке, и если через щели между крышей и последним венцом коробки дома эта разность давления не успеет выровняться. Крышу поднимет создавшаяся значительная результирующая сила, направленная вверх и равная произведению разности давления на площадь, а затем ветром крыша сбрасывается с дома (рис.7.3г).

7.2.5. Кавитация

Если увеличивать скорость движения жидкости по трубе (рис.7.2) или при том же самом расходе жидкости уменьшить самое узкое сечение трубы, то можно в этом сечении получить отрицательное давление. Действительно, из уравнения Бернулли и закона не накопления вещества в сечениях S1 и Smin трубы можно записать

(7.2.12)

Из этих уравнений легко получить выражение для минимального давления в самом узком сечении трубы :

(7.2.13)

Из данного соотношения видно, что если второе слагаемое в правой части по абсолютной величине будет больше, чем , то минимальное давление окажется «отрицательным», т. е. частицы жидкости, проходящее сечение трубы с «отрицательным» давлением будут подвергаться растяжению (такую жидкость называют «растянутой»). Однако, как отмечалось выше, жидкость не может находиться в растянутом состоянии длительное время. Она «вскипит» или, как говорят, сплошность жидкости нарушится в результате выделения пузырьков растворенного в ней газа. Так как при падении давления до «отрицательных» значений в жидкости выделяются пузырьки, заполненные паром жидкости или газом, растворённым в ней, или тем и другим в той или иной концентрации, то возникает так называемое явление кавитации, т. е. явление нарушения сплошности движущейся среды.

Явление кавитации играет очень важную роль в инженерной практике. Дело в том, что пузырьки газа, проходя самое узкое сечение трубы, попадают далее в область более высокого давления и схлапываются. Если такие пузырьки попадают на поверхность тела, то при их схлапывании возникают довольно значительные локальные давления, которые, в свою очередь, приводят к эрозии, т. е. разрушению, материала поверхности. Аналогичные явления возникают при быстром движении тел в жидкости, например, при вращении гребных винтов пароходов или лопаток гидротурбин. При этом так же образуются области «растянутой» жидкости, в которых выделяются пузырьки. Кавитация приводит к чрезвычайно быстрому их износу и выходу из строя и по настоящее время является предметом интенсивного изучения. Практически можно считать, что кавитация возникает тогда, когда в жидкости давление падает до давления насыщенных паров при данной температуре, т. е. когда

7.2.6. Трубка Пито

При обтекании тупого тела идеальной жидкостью на его поверхности всегда можно указать точку, в которой вектор скорости набегающего потока направлен по нормали и в которой скорость равна нулю (точка А на рис.7.4).

Рис. 7.4

Проведем в эту точку линию тока, которая, очевидно, начинается вдали от тела и заканчивается в точке А, которую называют точкой полного торможения потока или критической точкой, а линию тока – критической. Для этой линии тока можно записать уравнение Бернулли, которое для несжимаемой жидкости в отсутствии поля потенциальных сил имеет вид

(7.2.14)

Из этого уравнения следует

(7.2.15)

Как видно из (7.2.15), давление в критической точке определяется суммой давления в набегающем потоке и некоторой добавки, обязанной своим возникновением торможению жидкости в критической точке. Эту добавку, равную , называют скоростным напором. Последнюю формулу можно использовать для измерения скорости движения жидкости или скорости движения тела в неподвижной несжимаемой жидкости.

Прибор, при помощи которого проводят измерение скорости потока, используя эту формулу, называют трубкой Пито или трубкой Прандтля. Схематичное изображение такой трубки представлено на рис 7.5.Торцевое отверстие трубки Пито представляет собой «точку» полного торможения потока, в которой давление соответствует давлению полного торможения. Другой же торец U-образной манометрической трубки воспринимает через отверстие в боковой поверхности корпуса трубки статистическое давление в потоке . Очевидно, разность давлений уравновешивается давлением столба манометрической жидкости, равным . Тогда согласно (7.2.13) имеем

(7.2.16)

В формуле (7.2.16) g — ускорение силы тяжести, — плотность манометрической жидкости, r — плотность жидкости, скорость которой измеряется. В частности, это может быть и плотность газа, если измеряется скорость газа.

Рис. 7.5. Принципиальная схема трубки Пито

Таким образом, помещая трубку Пито в поток движущейся жидкости или газа и измеряя создаваемый перепад давления каким-либо манометром, можно довольно просто измерить их скорость. В результате длительного экспериментального и теоретического изучения в настоящее время выработан определенный стандарт, гарантирующий процентную точность в оптимальном диапазоне измерения скоростей. Рекомендации этого стандарта приведены на рис.7.5. Как видно из рисунка, давление в отверстии на боковой поверхности трубки будет равно давлению вдали от трубки в невозмущенном потоке лишь на расстоянии 3d от торца трубки. Любое другое расположение этого отверстия не гарантирует стандартную точность. Причины этого будут яснее при последующем изучении движений идеальной жидкости. Помещая трубку Пито на самолете, можно измерить скорость полета самолета относительно воздуха.

Механика сплошных сред — реферат

Для изучения профильных дисциплин специалистами в области ядерно-физических процессов, работающих на современных физико-энергетических установках, необходимы знания законов, описывающих свойства движения веществ в различных агрегатных состояниях.

Постановка курса имеет целью углубление знаний в области теоретической физики и дает возможность решения широкого круга прикладных задач движения сплошных сред.

В задачи изучения дисциплины входят: овладение студентами и использование в практической деятельности основных законов механики сплошных сред; овладение различными методами решения фундаментальной системы гидродинамических уравнений движения; получение сведений по основным свойствам среды при внешнем и внутреннем обтекании тел; привитие навыков экспериментального исследования различных физических явлений; изучение экспериментальной техники и методики проведения эксперимента.

Для изучения данной дисциплины студент должен владеть знаниями по курсам общей физики, высшей математики.

СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

1. Введение (1ч)

Предмет механики сплошных сред (МСС). О моделях механического движения. Последовательность модельных представлений в механике. Аналитическая механика материальной точки . МСС — дальнейшее обобщение механики точки и твердого тела. Понятие сплошной среды.

Бесконечно малые в МСС. Пределы применимости МСС. Элемент объема в МСС, характерный размер задачи. Бесконечно малый промежуток времени в МСС. Характерное время задачи.

2. Теория упругости (4 ч)

Деформация. Вектор деформации. Однородная линейная деформация. Тензор относительной деформации. Тензор деформации и тензор поворота.

Тензор поворота. Физический смысл тензора поворота. Тензор деформации. Главные деформации среды. Чистая деформация. Изменение объема тела при деформации.

Температурная деформация. Тензор теплового расширения. Коэффициент объемного расширения.

Силы массовые, объемные и поверхностные. Их определение. Тензор напряжений. Физический смысл компонент тензора напряжений. Давление.

Результирующая сила, действующая на единицу объема тела.

Работа внутренних сил. Упругие и пластические деформации. Основное термодинамическое равенство. Изменение внутренней энергии среды при деформациях. Изменение свободной энергии среды при деформациях.

Свободная энергия деформационного тела. Коэффициенты Ламэ. Тензор сдвига. Тензор всестороннего сжатия. Модуль всестороннего сжатия. Модуль сдвига. Положительность модулей.

Закон Гука. Изменение объема тела при деформации. Изменение свободной энергии деформируемой среды, выраженное через скалярное произведение тензора напряжений и тензора деформаций.

Однородная деформация (растяжение стержня). Граничные условия. Модуль Юнга и коэффициент Пуассона. Связь между коэффициентами Ламэ, модулем Юнга и коэффициентом Пуассона. Пределы изменения коэффициентов.

Уравнения равновесия изотропных тел.

Тензор скоростей деформации. Тензор скорости поворота.

Дифференцирование по времени интеграла по подвижному объему.

Уравнение непрерывности. Интегральная и дифференциальная формы уравнения непрерывности. Несжимаемая среда.

Уравнение движения сплошной среды. Интегральная и дифференциальная формы закона сохранения импульса. Субстанциональное и локальное описание движения сплошной среды.

Уравнение момента количества движения в МСС. Интегральная форма уравнения. Символ Леви-Чивита. Дифференциальная форма уравнения. Доказательство симметричности тензора напряжений.

Тензор плотности потока импульса.

Уравнение сохранения внутренней энергии. Внутренняя энергия единицы объема сплошной среды. Плотность теплового потока.

Вектор плотности потока полной энергии (вектор Умова). Физический смысл составляющих вектора Умова.

Фундаментальная замкнутая система уравнений движения сплошной среды. Количество уравнений. Количество неизвестных. Уравнение состояния. Уравнение Фурье для плотности потока тепла. Начальные и краевые условия. Существование и единственность решений. Феноменологические коэффициенты уравнений.

Тензор вязких напряжений. Коэффициенты сдвиговой и объемной вязкости.

Модели сплошных сред. Твердое тело. Жидкость. Газы. Время релаксации напряжений. Ньютоновские жидкости. Полный тензор напряжений для ньютоновских жидкостей и газов.

3. Идеальная жидкость (6 ч)

Определение идеальной жидкости.

Замкнутая система уравнений для идеальной жидкости. Тензор напряжений. Уравнение Эйлера. Уравнение сохранения внутренней энергии. Система уравнений. Изоэнтропическое движение. Плотность потока энтропии. Уравнение Эйлера в форме Громека. Граничные и начальные условия.

Уравнение Бернулли. Потенциальное движение жидкости. Уравнение стационарного, потенциального, изоэнтропического движения идеальной жидкости в поле силы тяжести. Уравнение Бернулли для сжимаемой и несжимаемой жидкости. Линии тока и траектории при стационарном и нестационарном движении. Трубка тока. Уравнение линий тока для стационарного движения. Уравнение Бернулли для нестационарного движения. Баротропное движение.

Примеры применения уравнения Бернулли. Скорость истечения несжимаемой идеальной жидкости из сосуда. Распределение давления в трубе переменного сечения. Кавитация. Трубка Пито. Критическая точка.

Влияние сжимаемости среды. Критерий для учета сжимаемости.

Вихревое движение. Теорема Томсона. Сохранение циркуляции скорости. Пределы применимости теоремы Томсона в реальных жидкостях. Вихревая трубка. Теорема Гельмгольца для интенсивности вихревой трубки. Одиночная вихревая прямолинейная нить. Вихревое движение по замкнутым траекториям. Примеры вихревых движений. Вихревые кольца. Вихревое движение в природе.

Потенциальное движение. Потенциал скорости. Уравнение Бернулли для нестационарного потенциального движения. Идеальная несжимаемая жидкость. Уравнение для потенциала скорости при потенциальном движении идеальной несжимаемой жидкости. (Уравнение Лапласа). Граничные условия.

Плоское движение несжимаемой жидкости. Функция тока. Свойства функции тока. Ортогональность линяй тока и эквипотенциальных линий.

Методы решения уравнения движения идеальной жидкости. Метод конформных: отображений. Обтекание бесконечного цилиндра. Парадокс Даламбера. Метод суперпозиции потенциальных потоков. Обтекание цилиндра с циркуляцией. Подъемная сила. (Эффект Магнуса). Теорема Жуковского. Примеры обтекания цилиндра с циркуляцией.

Графоаналитический метод. Непосредственное решение уравнений движения. Движение бесконечного цилиндра в идеальной несжимаемой жидкости. Нестационарность задачи. Присоединенная масса. Примеры влияния присоединенной массы на движение тел.

4. Вязкая жидкость (7 ч)

Уравнение Навье-Стокса. Граничные и начальные условия. Вихревое движение вязкой жидкости. Уравнение переноса интенсивности вихревого движения. Диффузия вихря.

Диссипация кинетической энергии в несжимаемой вязкой жидкости. Положительность динамического коэффициента вязкости.

Точные решения уравнения Навье-Стокса. Задача Куэтта. Плоское течение Пуазейля. Цилиндрическое течение Пуазейля. Профиль скорости, расход, сила трения. Использование формулы Пуазейля для измерения вязкости жидкости. Движение жидкости между двумя вращающимися цилиндрами. Распределение скорости, плотности и давления в зазоре. Момент вязких сил, действующих на цилиндры. Медленное обтекание шара вязкой несжимаемой жидкости. Задача Стокса, постановка задачи, результаты решения.

5. Теория подобия и моделирование (4ч)

Подобие в гидродинамике.. Безразмерная форма уравнения Навье-Стокса. Характерные величины. Критерии подобия Рейнольдса, Маха, Фруда, Стругала. Геометрическое подобие как непременное условие динамического подобия. Сила сопротивления. Коэффициенты сопротивления: коэффициент лобового сопротивления, коэффициент подъемной силы и коэффициенты боковой силы.

Аналитические коэффициенты сопротивления. Коэффициент сопротивления цилиндрической трубы, коэффициент сопротивления шара, при ламинарном движении жидкости.

Численное решение дифференциальных уравнений.

6. Турбулентность (4 ч)

Проблема устойчивости движения.

Устойчивость стационарного движения жидкости. Общая схема исследования на устойчивость стационарных движений вязкой несжимаемой жидкости. Малые возмущения. Комплексные частоты. Условие устойчивости. Критическое число Рейнольдса. Турбулентное движение. Опыты Рейнольдса по наблюдению движения вязкой жидкости в круглой цилиндрической трубе.

Характерные особенности турбулентного движения. Нестационарность и квазипериодичность движения. Критическое число Рейнольдса. Зависимость критического числа Рейнольдса от характера и величины возмущений.

Уравнения Рейнольдса. Средние и пульсационные скорости движение. Осреднение уравнений Навье Стокса. Тензор турбулентных напряжений. Турбулентная вязкость. Незамкнутость системы уравнений турбулентного движения. Понятие о методе Фридмана.

Теория турбулентности Прандтля. Гипотезы Прандтля. Двина пути перемешивания. Логарифмический профиль скорости.

Турбулентное движение жидкости в трубах. Гладкие трубы. Формула Блазиуса для коэффициента сопротивления. Закон распределения скорости по сечению трубы.

Формула Никурадзе для коэффициента сопротивления. Сопротивление шероховатых труб. Дополнительный критерий подобия. Результаты экспериментов с шероховатыми трубами.

Постановка и метод решения задач нестационарного течения жидкости.

7. Пограничный слой (2 ч)

Понятие о пограничном слое»

Уравнения Прандтля. Уравнения Прандтля о безразмерном виде. Подобное преобразование картины движения в пограничном слое при увеличении числа Рейнольдса. Толщина пограничного слоя.

Обтекание плоской полубесконечной пластины. Результаты численного решения. Сила трения, коэффициент сопротивления и толщина, пограничного слоя. Толщина вытеснения. Разгонный участок.

Отрыв пограничного слоя. Нахождение точки отрыва пограничного слоя. Хорошо и плохо обтекаемые тела. Способы управления пограничным слоем.

Турбулентный пограничный слой и кризис сопротивления. Экспериментальные результаты по измерению сопротивления шара в зависимости от числа Рейнольдса. Изменение характера обтекания шара при увеличении числа Рейнольдса.

8. Газовая динамика (2 ч)

Предмет газовой динамики

Скорость звука. Скорость звука и средняя тепловая скорость движения молекул. Скорость звука как термодинамический параметр. Выражение внутренней энергии энтальпии и энтропии газа через скорость звука.

Параметры газа в заторможенном потоке. Температура торможения. Примеры изменения температуры газа при движении.

Стационарный одномерный поток сжимаемого газа. Максимальная скорость движения. Критическая скорость.

Изменение плотности потока вещества вдоль трубки тока при дозвуковом и сверхзвуковом движении. Сопло Лаваля. Расчет сопла Лаваля.

Истечение газа из резервуара через сужающийся насадок. Формула Сен-Венана и Вентцеля. Звуковая диафрагма.

Представление об ударных волнах и скачках уплотнения.

9. Магнитная гидродинамика (4ч)

Особенности движения проводящей жидкости в магнитное поле.

Уравнения Максвелла. Ограничения класса рассматриваемых сред и движений. Изотропная проводимость жидкости. Пренебрежение токами смещения.

Уравнение движения проводящей жидкости в магнитной поле. Тензоры электрического к магнитного напряжений. Электрические массовые, магнитные массовые силы. Уравнение Навье-Стокса в магнитной гидродинамике. Уравнение непрерывности. Уравнение сохранения внутренней энергии. Диссипация энергии вследствие токов проводимости. Замкнутая система уравнений движения. Граничные условия.

Система уравнений для несжимаемой жидкости.

Тензор плотности потока импульса. Вектор Умова.

Принцип вмороженности магнитных силовых линий. Возможность значительного увеличения напряженности магнитного поля при сжатии вещества. Диффузия магнитного поля. Время релаксации магнитного поля в проводящей среде.

Задача Гартмана. Установившееся движение проводящей жидкости между двумя параллельными плоскостями в поперечном магнитном поле. Профиль скорости.

Магнитогидродинамические машины. Электромагнитные насосы. Преимущества и недостатки электромагнитных насосов. Индукционный насос. Электромагнитные насосы прямого действия. Приближенный расчет производительности электромагнитного насоса прямого действия. Магнитогидродинамический генератор (МГД-генератор). Оценка мощности МГД-генератора. Плазменные двигатели.

Одномерное движение проводящей жидкости в поперечном магнитном поле. Магнитное движение. Скорость распространения малых возмущений. Волны Альвена. Уравнение Бернулли в магнитной гидродинамике.

Практические занятия, их содержание и объем в часах

1. Распределение скорости и давления при движении газов и жидкостей в каналах (2ч).

2. Теория подобия и метод размерностей (2 ч).

3. Численное решение дифференциальных уравнений (2ч).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

Основной

1. Ландау Л. Д., Лившиц Е.М. Гидродинамика. М.: Наука, 1986.735 с.

2. Седов Л.И. Механика сплошной среды. М.:Наука, 1970. Т.1. 492 с.; Т.II.568 с.

Дополнительный

1. Фабрикант Н.Я. Аэродинамика. М.:ГИТТЛ. 1950. 814 с.

2. Прандтлъ Л. Гидроаэродинамика. Пер.с нем. М.: Изд-во иностр. лит., 1953.

3. Лойцянский Л.Г. Механика жидкости и газа. М.:Наука, 1970. 736 с.

Рабочая программа по курсу «Механика сплошных сред» для для стуентов специальности: «Ядерные реакторы и энергетические установки».

Составитель: Калинин Борис Алексеевич

Составлена 01.09.2000 стр. 9

Кафедра молекулярной физики УГТУ,
620002, Екатеринбург, УГТУ, 5-й учебный корпус