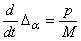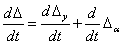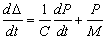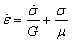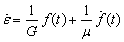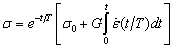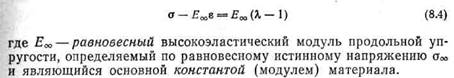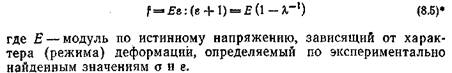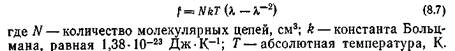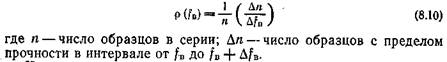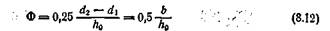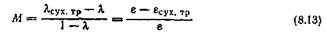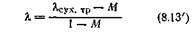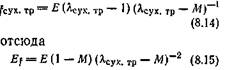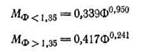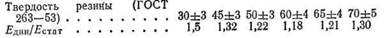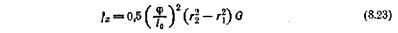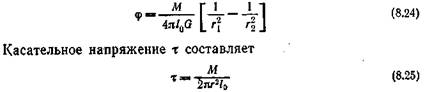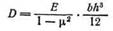Уравнение состояния резиновой полосы имеет вид

Примеры на соотношения Максвелла

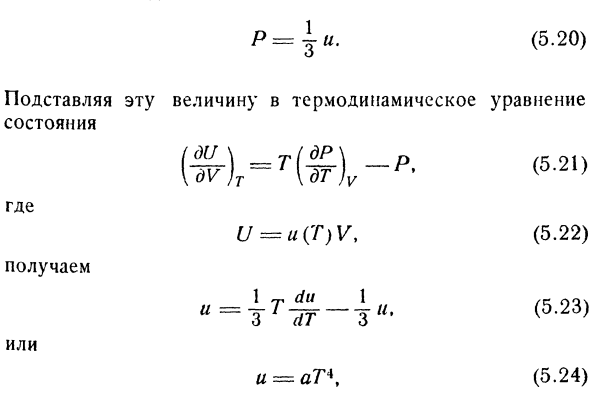
Примеры

• Соотношения Максвелла.Во-первых, мы преобразуем производные (dSjdV) T и (dSjdP) Р. Согласно (5.11)、 ДФ (ДГ \ ДТ)г-ДТ С= Так… (OS \ _ d2F (OS \ _ dU dVJr-OT0V и \ dR) r-dR OT Из уравнения(5.11) (* Л \ = Р(Ш)= Г \ дв) \ Т ОП ^ ） Откуда? Формула (5.16) называется отношением Максвелла.Они оказались полезными в ряде случаев (например, см. Главу 5,§ 3, пункт 3).

• 2.Термодинамическое уравнение состояния.Здесь мы рассмотрим производные (dU, dV) T и (dN / dR) m, которые фигурируют в описаниях экспериментов Гей-Люссака и Джоуля-Томсона(см. Главу 2, Главу 7 и Главу 2).Мы уже работаем над превращением первого из них в парня. 2,§ 7, пункт 1 Но от более простого способа, а именно отношения 1518.） Получить уравнение (дю ДТ)V л (5.19)） Это называется термодинамическим состоянием equation.As увиденный в chapt. 2,§ 7, параграф 2.Левая часть этих уравнений в частных производных определяет изменение температуры газа при адиабатическом расширении.Приравнивание левой части уравнения(5.19) к пуле дает закон идеального газа Бойля-Марио-Гая-Руссака (см. задачу»с»в главах 2, 7 и 2).） — Спросил я.

Уравнение состояния резиновой ленты имеет вид Где / — напряжение, a = 1.3.103 dyn!Град, I-длина,/ 0 = 1 м. a. указывает, что внутренняя энергия зависит только от температуры. а. полоса подвергается обратимому изотермическому растяжению при температуре 3°С, длина изменяется от 1 до 2 м. Найти работу, выполненную на полосе и количество поглощенного тепла. c. если полоса растягивается до изоэнтропийной, какова будет конечная температура полосы?

Удельная теплоемкость при постоянной длине вычисляется Ct-1.2 J (степень (задачи, предложенной в тесте Оксфордского университета 1962 года).） И решение тоже.Термодинамическая идентичность Т ДС-дю-Ф дл. В результате f-dFjdl и термодинамическое уравнение состояния принимают вид: Итак, поскольку (dU / df) T = 0 [(di / d/) m = — (dUjdl) T (dHdf) T], U может быть только функцией T. a. работа, выполняемая при изотермическом напряжении, осуществляется в г г ’/ 21/2 / ГП’ — 2-4 Если вы представляете все значения системы CGS、 ХЛ 1×1 ЧПУ G 2002 году я 1002 1002 100П ® м,Р7 ОП, 1.3.103.Зоопарк. + = D (7 = 0, поэтому поглощенное тепло 3 9. −3.9 J В =-А—0.93 коэф. 4.1 ОО В.

И так энтропийно равная работа f / d / = Cz (300-rKOH） Людмила Фирмаль

Если объединить последнее уравнение с уравнением состояния, то получим: Здесь Интеграл захватывается изэнтропиями. Изоэнтропийное отношение между I и T имеет следующий вид: 0 = сл ДТ-fdly Или dt. = 0、 Ct в T—f — — y-j = const、 = 100А = 1.3. 105 эрг / город. Да. / 2 I * Два Г / 2/2- Т. В. 300. Когда Ct = 1.2 J подставляется、 G = 300 ^ 0108 = 303,3°.

• 3.Излучение черного тела.Поскольку электромагнитное поле не является материальным, оно не может рассматриваться в рамках термодинамики.Но это не так.Замкнутые полости, поддерживаемые при постоянной температуре, постоянно заполняются электромагнитным излучением всех длин волн, которое может распространяться во всех directions.It оказывает давление на стенки полости и несет energy.It функция давления, так же, как температуры и volume.In короче говоря, такая замкнутая полость, заполненная излучением, как впервые установил Больцман (1889), представляет собой систему, в которой справедливо действуют законы термодинамики applied.

На этот раз учитель Больцмана Йозеф Штефан уже вывел из экспериментальных данных, что интенсивность излучения из отверстия в замкнутой полости, температура стенки которой везде одинакова, пропорциональна Т4.Из этого результата Больцман сделал правильный вывод, что плотность энергии и (T) равновесное излучение пропорциональны 4-степени температуры, и использовал термодинамику и электродинамику для получения этой зависимости.Максвелл, основываясь на своей теории электромагнетизма, установил, что давление, оказываемое полем изотропного излучения, составляет 73 градуса плотности энергии. р = 4″. Эта величина подставляется в термодинамическое уравнение состояния рффл. К Куда? дв)Т — [д’м)у = у(Т)в、 _ 1-дю 1

Мы получаем Или «»З ^ г«!’ И= То есть закон Стефана Больцмана.Коэффициент пропорциональности a явно является универсальной константой. Отсюда можно получить и другие термодинамические функции поля излучения. Объединение (5.20) и (5.24) с отношением Максвелла (5.16) (5.25） Например、 (5.26） Несовершенство классической теории проявлялось в том, что невозможно было предсказать распределение энергии излучения по разным длинам волн.

Это стало отправной точкой для революционного открытия Планка, который ввел гипотезу действия квантов.Но даже без квантовой теории можно кое-что сказать о распределении интенсивности так называемого излучения черного тела. В равновесном состоянии поле излучения может быть представлено набором стоячих волн в полости объема V. ВЗ, 3.、 (5.27） Тогда для образования стоячей волны необходимо, чтобы ее частота v удовлетворяла уравнению (5.28)） Где c-скорость света,/, t и n-целые числа.

Для макроскопического размера L, количество vLJc будет очень большим для всех длин волн c interest.So, число «собственных колебаний» (5.28), частота которых меньше v, GV пропорционально числу точек в сфере радиуса vL / c, имеющих целочисленные координаты f, m, n. (5.29） Г-ВВ. \ DOI выбрал для рассмотрения кубическую полость V, но, согласно немецкой теореме Вейля (1912), этот асимптотический результат не зависит от формы полости. Физический смысл целых чисел I, m и n таков:это число узлов стоячих волн вдоль соответствующих граней куба.

Они обладают следующими замечательными инвариантными свойствами: Если вы медленно меняете объем полости, то узловые грани каждой волны смещаются, а набор цифр f, m и n-нет changed.As для частоты собственных колебаний мы испытываем смещение, определяемое отношением к медленному расширению V — > V — \ — bV. (5.30)） Вы можете увидеть это, дифференцируя константы f, m и n(5.28).Таким образом, при постепенном изменении параметра V величина.

Собственная вибрация всех частот v (f, m, n).Это понятие играет очень важную роль в термодинамике.Это связано с постепенным изменением механических параметров-обратимым процессом теплоизоляции.Таким образом, существование параметрического инварианта в динамике системы подразумевает существование некоторого рода отношения, представляющего собой изоэнтропийное отношение между ее термодинамическими свойствами. parameters.In в рассматриваемом случае, согласно (5.26), изоэнтропийная зависимость поля излучения между объемом и температурой равна УУ3 = const. (5.32)） «)

Значение типа W называется параметрическим инвариантом. Людмила Фирмаль

Больцман использовал медленное термоизоляционное преобразование параметров механической системы, но важную роль в этом методе играет наличие P.It впервые был понят Эренфестом (см. Его обзорную статью[15]).Параметрические инварианты иногда называют адиабатическими инвариантами. Поэтому, если сравнить соотношение (5.31) с (5.32), то обратимое преобразование теплоизоляции будет (5.33） = Неизменный. Теперь мы можем сделать некоторые общие выводы о распределении лучистой энергии p (v)по различным частотам. (5.34)）

Сначала подумайте об энтропии. Поскольку расширение спектра (например, с помощью решетки) является обратимым процессом, энтропия равна сумме вкладов каждого frequency.In кроме того, если адиабатический обратимый процесс 5 = const, то частота и температура могут попадать в отдельные члены этой суммы только в виде адиабатического инварианта v / 7, поэтому разложение 5 должно принимать вид: (5.35） Напишите на бланке разложение энергии Ф / = 2е(в. Т)(5.36） В. Согласно «(5.24) и (5.26)」 Ы-ы -, (5.37） Он приходит к выводу, что частное e (v, T) / T должно быть функцией v / 7 для каждого члена sum.So, тепловую энергию е, соответствующую собственным колебаниям, следует записать в виде: Е(В. р)= в /(- Ф); (5.38） Для этого ^ = С(т)•(5-39）

В соответствии с (5.29), плотность спектра настолько высока, что сумма может быть заменена интегралом. 2 = J dG ^ V J v2 dv. (5.40） В. Из соотношений (5.38) и (5.39) видно, что спектральное распределение энергии, фигурирующее в уравнении (5.34), имеет вид: п(п,Γ)= constvV(5-41） Максимальная интенсивность излучения черного тела определяется соотношением 3v2 / +(t»)/, = = 0 ’или константаг, (5.42） То есть пропорционально увеличению температуры она смещается на более высокую частоту (закон Вены).

Определение типа функции/является задачей статистической mechanics.It была эта проблема, которую оказалось невозможно решить с помощью классической теории.И наоборот, выводы термодинамики [соотношения (5.24), (5.26) и (5.41)] бесконечно применимы, поскольку они основаны только на понятиях 2 положений механики системы, то есть формулы Максвелла для радиационного давления (5.20) и параметрической инвариантности.

Сила в квантовой теории. Вызов.Если предположить, что величина энергии, соответствующая уровню энергии одночастичного одноатомного нерелятивистского разреженного газа, пропорциональна V〜v, то внутренняя энергия такого газа оказывается равной 3/2 ПВ. (Среди задач, предложенных на экзамене Оксфордского университета 1962 года） Решение.Энергия каждой молекулы Где/ — функция квантового числа, массы молекулы и др.Мы используем теорему квантовой механики следующим образом: Его функция/не изменяется, даже если изменяется громкость slowly.So, энергетический уровень изменяется медленно, но квантовое число не изменяется.Этот факт тесно связан с классической параметрической инвариантностью, рассматриваемой применительно к задаче излучения черного тела.

С тех пор Поскольку внутренняя энергия равна сумме 2 е, взятой для всех молекул, можно сделать вывод: Два / U = V 1X X функция адиабатического инварианта、 Или UV, 3 =постоянная вдоль равной энтропии.Отсюда、 Или ПВ ^ у、 Если вам нужно доказать.Заметим, что этот результат является более общим, чем уравнение состояния PV-RT. T = = не применяется вблизи 0.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

РЕОЛОГИЯ

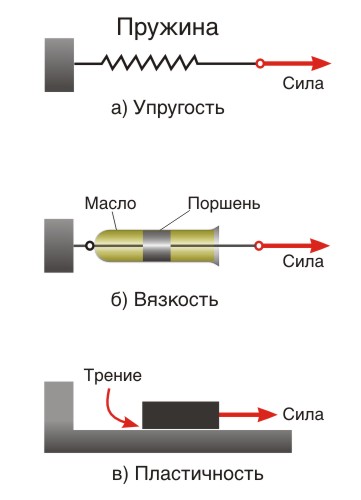
РЕОЛОГИЯ – наука о деформациях и текучести сплошных сред, обнаруживающих упругие, пластические и вязкие свойства в различных сочетаниях. Упругие деформации возникают в теле при приложении нагрузки и исчезают, если нагрузки снять; пластические деформации появляются только в том случае, когда вызванные нагрузкой напряжения превышают известную величину – предел текучести; они сохраняются после снятия нагрузки; вязкое течение отличается тем, что оно возникает при любых сколь угодно малых напряжениях, с ростом напряжений увеличивается скорость течения, и при сохранении напряжений вязкое течение продолжается неограниченно. Еще одно свойство, которым могут обладать среды, изучаемые реологией, – это высокоэластичность, характерная, например, для резины, когда резиновая лента допускает десятикратное растяжение, а после снятия нагрузки практически мгновенно восстанавливает первоначальное состояние.

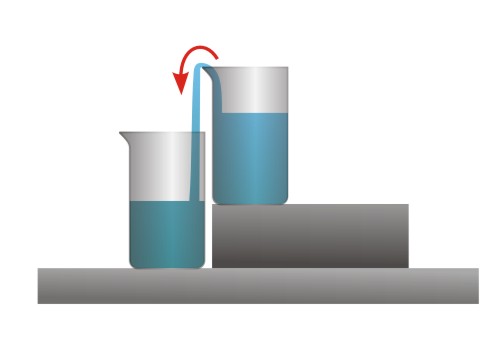
Типичный реологический процесс – это сравнительно медленное течение вещества, в котором обнаруживаются упругие, пластические или высокоэластические свойства. Само слово реология происходит от греческого rew – течение; афоризм «все течет» по-гречески звучит panta rei – (па’нта ре’и). Реологические явления проявляются во многих природных процессах и в большом числе технологических. Очень многочисленны вещества, участвующие в таких процессах: это породы, составляющие земную кору, магма, вулканическая лава, это нефть и глинистые растворы, играющие важнейшую роль в добыче нефти; влажная глина, цементная паста, бетон и асфальтобетон (смесь асфальта и песка, которой покрывают тротуар), это масляные краски – смесь масла и частиц пигмента; это растворы и расплавы полимеров в процессе изготовления нитей, пленок, труб путем экструзии; наконец, это – хлебное тесто и тестообразные массы, из которых изготовляют конфеты, сосиски, кремы, мази, зубные пасты, это твердое топливо для ракет; это, наконец, белковые тела, например, мышечные ткани. В этот не полный перечень «реологических» сред входят как тела, которые естественно считать твердыми (бетон), так и жидкие – нефть. Еще один опыт можно провести с высокомолекулярным раствором полиэтиленоксида в воде. Если, наклонив стакан А, начать переливать из него раствор в нижний стакан Б (рис. 1), а потом аккуратно вернуть стакан А на место, то окажется, что тонкая струйка раствора продолжает перетекать из верхнего стакана в нижний: интересно, что эта струйка сначала поднимается вверх по вертикальной стенке стакана А, а затем, переливается через край и стекает вниз, в стакан Б – это своеобразный сифон, но без сифонной трубки.

Совсем простой опыт невольно ставит тот, кто испачкал пальцы смолой, резиновым клеем или густым сахарным сиропом: попытка разлепить пальцы приводит к образованию упругих нитей, которые вытягиваются из текучей среды. Именно так образуется паутина и шелковая нить.

Реология позволяет понять, что при быстрых воздействиях все тела ведут себя как твердые, при медленных – текут. Но понятия «быстрый» и «медленный» для разных сред различны. Удар о воду на скорости 200 км/час мало чем отличается от удара об асфальт – вода ведет себя как твердое тело (ее текучесть не успевает проявиться). Железобетонный столб, косо прислоненный к стене, через месяц оказывается кривым – бетон течет; струны на гитаре, оставленные в натянутом состоянии, снижают тон – в результате медленного течения материала их длина чуть-чуть увеличилась, соответственно, уменьшилось натяжение – их приходится подтягивать. Горные породы за геологические периоды сминаются в складки – образуются горные системы. Без вычислений ясно, что диапазон времен в реологических явлениях простирается от долей секунды до миллионов лет.

Итак, механические свойства разных реологических сред, во-первых, весьма разнообразны, и, во-вторых, оказываются существенно различными в зависимости от условий нагружения.

Очень многие реологические среды являются дисперсными системами двух или трех фаз: это мелкие твердые частицы, распределенные в вязкой жидкости (суспензия или гель, если твердая фаза преобладает), или это мелкие капельки одной жидкости в другой – эмульсия, или пузырьки воздуха в жидкости (пена), и т.д. Но, тем не менее, реология рассматривает такую среду как однородную, но обнаруживающую такие же механические свойства, как и те, что установлены в опытах с реальным конкретным материалом. Этот подход, характерный для механики сплошных сред, позволяет избежать трудностей, связанных с изучением механизмов взаимодействия фаз, и сравнительно просто описать основные черты поведения реологических сред при воздействии на них заданных нагрузок. Такие теории называются феноменологическими.

Математическая модель механических свойств данной среды задается уравнением, связывающим напряжения, имеющиеся в окрестности некоторой точки среды, и деформации, возникающие вследствие этого, причем в это уравнение могут входить и скорости напряжений и деформаций, т.е. их производные по времени, и интегралы по времени от напряжений или деформаций.

Это уравнение называется реологическим уравнением состояния среды или ее определяющим соотношением, и играет роль, аналогичную роли уравнения состояния идеального газа, нужно только иметь в виду, что уравнение состояния газа гораздо точнее отражает свойства конкретного газа, чем реологическое уравнение – свойства некоторой вязко-упруго-текучей среды, что объясняется очевидной причиной – очень высокой сложностью тех сред, которые изучает реология.

Определяющее соотношение должно быть сформулировано как связь тензоров напряжений и деформаций на основе всех известных опытных данных, но сами опыты эту связь не устанавливают, а лишь показывают ее проявления в некоторых частных случаях.

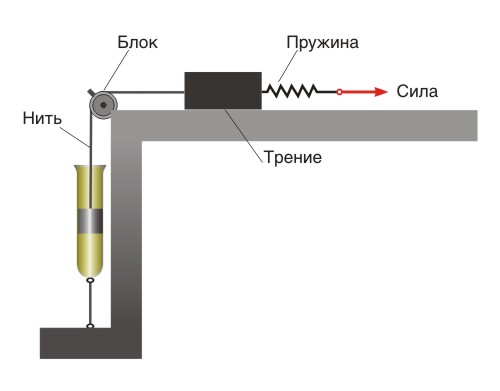
Простой и наглядный способ построения реологического уравнения состояния состоит в том, что каждое основное свойство среды можно смоделировать подходящим элементом, то есть упругость – пружинкой, вязкость – поршнем в цилиндре с вязкой жидкостью, пластичность – элементом с сухим трением (рис. 2).

Соединив тем или иным образом эти элементы, получают модель образца для механических испытаний, свойства которого в общих чертах можно определить теоретически. Это позволяет, изучив опыты с конкретным материалом, подобрать такое соединение элементов, чтобы обеспечить качественное соответствие реальным опытам, подбирая жесткость пружинки, вязкость масла в поршне, величину коэффициента сухого трения, можно добиться достаточно точного совпадения экспериментальных кривых и их модельного представления (если, конечно, структура модели правильно организована и достаточно богата для описания данного материала). Если модель из элементов построена, то написание математического соотношения производится по определенным правилам, причем сравнительно простым.

Модель, составленную из пружинок и поршеньков, можно только растягивать, но растяжению в модели могут соответствовать и сжатие, и сдвиг, и объемная деформация в натурной среде.

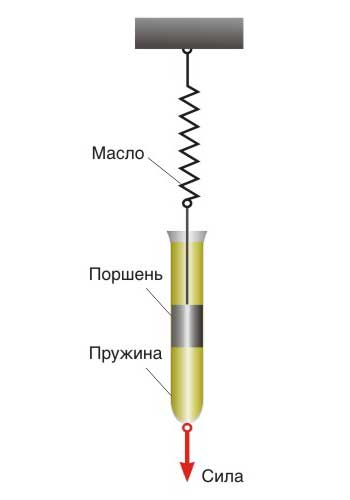
Можно построить модель вязко-упругого тела, последовательно соединив упругий и вязкий элементы (рис. 3).

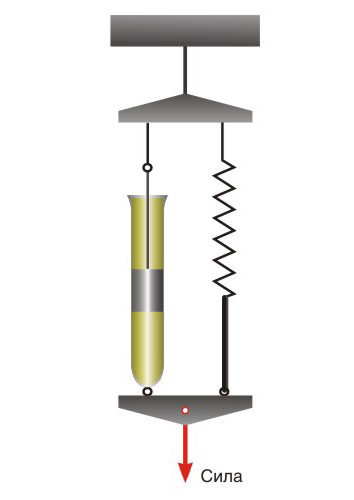
Если эту систему быстро нагрузить (дернуть), то вязкий элемент не успеет сдвинуться с места и будет вести себя, как замороженный, а деформацию возьмет на себя пружина – и модель ведет себя как упругое тело. Наоборот, при медленном нагружении, например, при постоянной силе, к некоторой небольшой постоянной деформации пружины прибавляется в принципе неограниченно возрастающая деформация вязкого элемента, т.е. модель ведет себя как упругая жидкость, которую называют жидкостью Максвелла (а также телом или моделью Максвелла). Эта жидкость не подчиняется закону вязкости Ньютона и поэтому называется неньютоновской жидкостью.

Закон Гука применительно к пружине имеет вид

где D_g – упругое удлинение пружины, P – сила, C – жесткость пружины.

Для вязкой жидкости справедлив закон Ньютона, который применительно к перемещению поршня в цилиндре дает

здесь D_a – вязкое смещение поршня в цилиндре, M – коэффициент вязкого сопротивления.

Уравнение, описывающее зависимость удлинения модели (рис. 3) D от величины силы 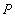получают, сложив упругое удлинение пружины D_g и вязкое удлинение системы «цилиндр-поршень» D_a ; но поскольку скорость вязкого удлинения матрицы d D_a / dt известна, то удобнее найти скорость удлинения модели d D / dt по формуле

Таким образом, уравнение модели имеет вид:

Чтобы теперь перейти от модели к сплошной среде, удлинение D l заменяют деформацией e , силу P – напряжением s , жесткость C – модулем упругости G, а коэффициент вязкого сопротивления M – вязкостью жидкости m , в результате получается определяющее реологическое уравнение среды Максвелла в виде:

(точка означает производную по времени). Если задано напряжение как функция времени, s = ¦( t ) , то скорость деформации легко находится по формуле

Если же деформация задана как функция времени, то реологическое уравнение Максвелла представляет собой дифференциальное уравнение относительно t , решение которого имеет вид

(здесь t₀ – начальное напряжение при t = 0, а величина 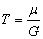называется временем релаксации). Пусть в начальный момент к образцу прикладывается усилие, вызывающее напряжение s₀ ; при этом в образце возникает деформация e₀ . Если эту деформацию поддерживать постоянной, ( e = 0) , то напряжение t , согласно (2), убывает со временем экспоненциально, т.е.

и за время T уменьшается в e раз, (e » 2,71828 – основание натуральных логарифмов). Таким образом, время релаксации T характеризует скорость убывания напряжений в описанном процессе при e = const, который называется процессом релаксации.

Реологическое уравнение Максвелла пригодно для качественного описания процессов в стекловидных и полимерных материалах. Для хорошего количественного описания используются более сложные модели.

Выражение для s = f(t) содержит интеграл по времени от начала процесса до текущего момента; поэтому значение напряжения s в момент t зависит от значений e во все предшествующие моменты от 0 до t, поэтому такие модели называют «материалами с памятью».

Для описания реологических свойств суглинка, имеющего структуру геля, в котором частицы песка соединяются цепочками коллоидных частиц глины, а промежутки заполнены водой, Кельвин предложил схему, в которой упругий и вязкий элементы соединены параллельно, т.е. так, что их деформации одинаковы (рис. 4).

Соответствующее реологическое уравнение получается аналогично тому, как это сделано для среды Максвелла, но с учетом того, что в модели Кельвина одинаковы деформации элементов, а общее напряжение получается суммированием напряжений в вязком и упругом элементах:

Анализ показывает, что среда Кельвина является твердым телом, похожим на губку, пропитанную вязкой жидкостью.

Примером более сложной модели является среда Бингама, модель которой представлена на рис. 4. Если увеличивать силу P, то сначала деформируется только пружина; затем, при определенном значении силы P, преодолевается сила трения бруска о поверхность и начинается его движение, сопротивление которому оказывает не только трение, но и вязкое сопротивление поршня в цилиндре (рис. 5).

Считается, что реология началась именно с этой модели, не укладывающейся в рамки взаимодействия классических сред – упругого тела и вязкой жидкости. Среда Бингама была введена для описания поведения свежей масляной краски, когда было установлено, что она является пластическим твердым телом, а не вязкой жидкостью.

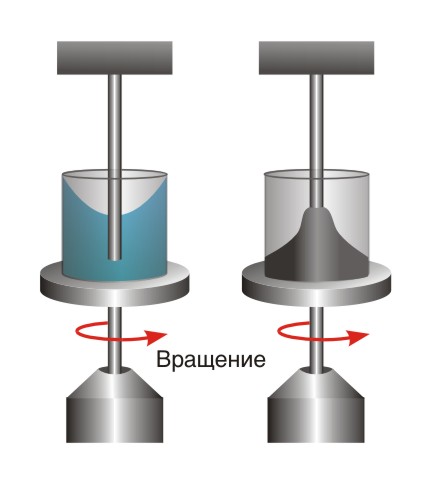
Реологические модели, получаемые путем комбинирования основных элементов (упругость, вязкость, трение) качественно описывают поведение под нагрузкой реальных сред, но наблюдаются при этом значительные количественные отклонения. Но известны эффекты, для описания которых в настоящее время еще не создана удовлетворительная теория. В первую очередь, это так называемый эффект Вайсенберга. Он проявляется, в частности, в следующем опыте (рис. 6): Пусть есть два одинаковых стакана – один с ньютоновской вязкой жидкостью, например, с растительным маслом, другой – с концентрированным раствором высокополимерного вещества (например, сладкого сгущенного молока); оба стакана приводятся во вращение вокруг своих осей. Сверху в стаканы опущены неподвижные круглые стержни. В стакане с маслом видна ожидаемая картина – жидкость принимает форму тела вращения с параболической поверхностью, вертикальная координата которой возрастает с удалением от центра. Но в другом стакане жидкость начнет медленно подниматься по центральному неподвижному стержню, в результате чего уровень поверхности у оси оказывается выше, чем у краев.

Не менее интересен и «эффект Томса». В 1940-х многие исследователи замечали, что течение жидкости по трубопроводу сильно облегчается (снижается гидравлическое сопротивление), если в низкомолекулярную жидкость добавить очень малое (доли процента) количество растворимого полимера. Оказалось, что можно достигнуть четырехкратного снижения гидравлического сопротивления воды в трубе, добавляя несколько миллионных долей (по весу) подходящего высокомолекулярного вещества. Этот эффект используется в некоторых нефтепроводах, пожарных шлангах; есть исследования по снижению кровяного давления у животных.

Изучение реальных сред со сложными свойствами не обязательно относят к реологии: теория неньютоновской жидкостей, теория вязкоупругости и вязкопластичности, теория ползучести металлов при высоких температурах, механика природных процессов – это самостоятельные научные направления, с которыми связаны многие важнейшие достижения как в области теории, так и в области практики – от медицины до космоса, от снежных лавин до дрейфа континентов.

Рейнер М. Деформация и течение. М., 1963
Рейнер М. Реология. М., Наука, 1965
Бленд Д. Теория линейной вязкоупругости. М., 1965
Работнов Ю.Н. Теория ползучести. М., Наука, 1966
Лодж А.С. Эластичные жидкости. М., 1969
Шульман З.П. Беседы о реофизике. Минск, Наука и техника, 1976

Аналитическая зависимость между напряжением и деформацией резины и ее механические свойства

Растяжение в одноосном нагружении. При одноосном растя­жении с постоянной скоростью кристаллических материалов до ве­личины деформации, отвечающей пределу упругости (пропорциональности), наблюдается линейная зависимость между условным напряжением f (в 10 Н/см 2 ) и соответствующей ему относительной деформацией е. Для различных материалов их пределы пропорциональности различны как абсолютно, так и относительно к их пре­дельной деформации при разрыве.

Материалы, обладающие (наряду с упругой) высокоэластиче­ской деформацией — каучук, резина, некоторые пластмассы, а также текстильные изделия, способные при одноосном нагружении к значительно большим растяжениям, чем, например, сталь и раз личные металлы — линейную зависимость f — e показывают лишь на весьма небольших начальных растяжениях. В целом у этих материалов, несмотря на большую обратимость деформации, за­висимость f — е нелинейна и обычно не монотонна. Следовательно, такие материалы, как не отвечающие известному положению Гука, нельзя охарактеризовать одним постоянным значением модуля продольной упругости Ef, рассчитываемого по условному напряже­нию f. На участке нелинейной зависимости модуль материала Ef можно определять лишь в дифференциальной форме.

Применяемый иногда местный модуль (модуль по хорде) как отношение f/ef не дает конструкционно значащей оценки мате­риала. Столь же несостоятельна применяемая в лабораторной практике оценка свойств резины условным напряжением, отвечаю­щим растяжению на 100, 300 или 500% против начальной длины образца. Эти так называемые «модули» представляют собой лишь ординаты некоторых промежуточных точек кривой f — е, но не константы материала.

Для расчетно-конструкторских целей желательно, чтобы анали­тическая зависимость напряжений и соответствующих им дефор­маций резины была выражена через одну, имеющую физический смысл, характеристику материала, не зависящую от деформации. Практически удобно определять деформацию не относительным удлинением е, а величиной л, отношением текущей и начальной длин образца (относительной длиной образца):

Установление, с большим или меньшим приближением, зависи­мости между f (или о) и X для материалов, обладающих высоко эластическими свойствами, возможно: или теоретически, путем вы­числения искомой зависимости из свойств той или иной механиче­ской модели высокомолекулярного соединения, или путем подыскания уравнения экспериментально найденной зависимости.

Теоретическое установление зависимости напряжение — дефор­мация резины для высокоэластического ее состояния исходит из положения, что равновесное деформированное состояние опреде­ляется высокоэластической составляющей и что величиной упругой энергетической составляющей деформации можно пренебречь.

Рассматривая равновесную высокоэластическую деформацию резины как явление ориентации цепей молекулярных звеньев кау­чука в силовом поле, Г. М. Бартенев предложил для одноосной деформации растяжения резины следующее уравнение

Уравнение (8.4) применимо для мягких резин с содержанием связанной серы до 8%, но без учета влияния химических про­цессов в период нахождения образца под нагрузкой; последнее при­водит к условно равновесному модулю. Показано также, что уравнение пропорциональности а и е в ограниченных, но практи­чески достаточных пределах деформации с достаточным при­ближением может быть принято не только для равновесной де­формации, но и для статической, а равно и для непериодической динамической, но с другим в каждом конкретном случае модулем материала, зависящим от режима деформации и температуры. Под статической деформацией здесь понимается деформация в равновременном режиме, когда независимо от величины принятой де­формации одинаково время действия силы; под непериодической — динамический равноскоростной режим.

С учетом сказанного, для условного напряжения f при растя­жении справедлива будет приближенная зависимость

По числовому значению модуль Е занимает некоторое проме­жуточное место между мгновенным модулем Е₀, определяющим уп­ругие свойства резины в начальный период деформации, и высоко­эластическим равновесным модулем Еоо. Следуя уравнению (8.5), найдем дифференциальный модуль как производную от напряже­ния по деформации:

В физическом смысле Е по уравнению (8.6) при % Ш 1 представ­ляет модуль начальной деформации в соответственном режиме (то же относится и к E_f при этом значении X).

Уолл предложил следующее уравнение зависимости f — К для ненаполненной резины из натурального каучука

Если это уравнение привести к эмпирическому виду, позво­ляющему проверить его в статиче­ской или непериодической динами­ческой деформации, то получим

По физическому смыслу G в уравнении (8.9) при представ­ляет собой модуль сдвига, равный 1/3 Е для начальной деформации, как это и следует из зависимости G = £ : 2Х (1+M). Для изотроп­ных материалов при малых дефор­мациях и коэффициенте Пуассона м = 0,5.

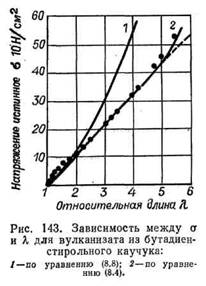
При растяжении ненаполненного вулканизата из бутадиен-сти-рольного каучука до л = 4 — 5 линейное уравнение (8.4) лучше согласуется с экспериментом (рис. 143), чем уравнение (8.8). Для наполненных вулканизатов уравнение (8.4) применимо при­мерно до л = 1,5.

Предел прочности резины при разрыве (как ус­ловный f_B, так и истинный о_в) зависит от ряда факторов. Поэтому в лабораторных испытаниях резины, следуя ГОСТ 270—64, приме­няют образцы установленной формы и размеров в виде двухсто­ронней лопатки, и испытание ведут со скоростью перемещения ниж­него зажима 500 мм/мин. Для инженерных расчетов необходимо было бы уяснение зависимости между пределом прочности резины в стандартных условиях испытания и в изделиях в условиях эксплуатации. Некоторое представление об ожидании такой зависимости следует из данных Г. М. Бартенева, полученных при испытании на разрыв образцов резины в форме стандартных двух­сторонних лопаток различной толщины: 2,2; 1,2 и 0,4 мм. В каж­дой из таких серий испытывалось не менее 100 образцов. Резуль­таты испытаний приведены на рис. 144, где по оси абсцисс откладывался найденный предел прочности, а по оси ординат функция распределения предела прочности р(f_в), рассчитываемая по формуле

Как видно из рис. 144, с уменьшением толщины кривые сме­щаются в сторону больших величин предела прочности, но разброс данных при этом увеличивается. Кривые для ненаполненной ре­зины отвечают нормальному распределению, и наивероятнейшая прочность может быть рассчитана как средняя арифметическая при заданной толщине образцов. В то же время относительный разброс прочности практически не зависит от толщины образцов.

При очень медленном растяжении, отвечающем установлению состояния, близкого к равновесному, предел прочности резины за­висит от степени поперечного «сшивания» и от прочности химиче­ских связей. При конечной же скорости растяжения решающее значение имеют связи межмолекулярного взаимодействия. При прочих равных условиях чем полярнее каучук, тем прочнее мягкий вулканизат. Чем выше скорость растя­жения, тем выше предел прочности (табл. 6).

В конструкции и эксплуатации РТИ могут быть различны не только скорость деформации и толщины образцов, но также другие геометрические размеры, форма образцов, виды и режимы дефор­мации и возможность концентрации на­пряжений. Все это в той или иной мере влияет на величину предела прочности в изделии и на срок службы изделия.

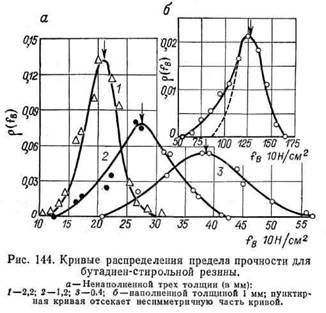
На рис. 145 показана зависимость между нагрузкой Р и относительным удлинением е при растяжении цилиндри­ческих образцов резины одного диаметра, но различной толщины (длины),привулканизованных к металлическим шай­бам (так называемым «грибкам»). Из рис. 145 видно, что чем тоньше образец, тем меньше его относительное удлинение при заданном Р; чем толще образец, тем относительное его удлинение больше и тем сильнее сказывается появление на нем «шейки» при растяжении. Одновременно с появлением шейки возникает и растет составляющая напряжения среза. Образец не имеет одинакового напряжения по сечениям, нормальным к на­правлению растягивающей силы. Разрыв начинается там, где снаружи или внутри образца было раньше какое-либо ослаблен­ное место (надрезы, трещины, полости); затем такой разрыв раз­растается и приводит к вазвушению образца.
струкции, работающие на растяжение, мало употребительны (характерное исключение составляют амортизационные шну­ры).

Сжатие. Конструкции, в которых резина подвергается одно­осному статическому или динамическому сжатию, находят более широкое применение. Сжатие образца резины при одноосном нагружении, проводимое между двумя параллельными плитами, мо­жет осуществляться в двух различных условиях: со смазкой или без смазки опорных поверхностей. Так как трение опорных поверх­ностей образца по плитам препятствует свободному расширению образца в боковом направлении, то боковая поверхность частично изгибается и приходит в контакт с плитами.

Применяя смазку опорных поверхностей и плит, можно облегчить скольжение образца по плитам. В этом случае, даже до значитель­ного уменьшения высоты, образец все же сохраняет форму цилиндра. То же происхо­дит в случае применения цилиндрических об­разцов с конусными впадинами на опорных поверхностях (рис. 146). Некоторую ана­логию сжатия без трения можно видеть на примере уменьшения толщины тонкостенного резинового надувного шара (шара пилота), растягиваемого внутренним давлением газа. Подобное этому напряженное состояние можно наблюдать при двуосном растяжении тонких крестообразных образцов резины.

Экспериментальная кривая зависимости f— е сжатия, в отличие от кривой при рас­тяжении, монотонна. Эту кривую Ариано принимал за равнобокую гиперболу с асимптотами, параллельными осям напряжений и деформаций.

Действительно, при растяжении стенок резинового полого шара, когда диаметр шара увеличивается, например до семикратного размера, толщина стенки уменьшается до 0,02 начальной, что дает а = —0,98. Если в уравнении (8.11) принять а = —1, то приходим к уравнению (8.5) с Е = С. Для а = fл уравнение (8.11) линейно. Напряжение f (или o) имеет знак минус.

Линейная зависимость по уравнению (8.4) сохраняется и для случаев равновесного и статического сжатия резины с применением смазки; сохраняется зависимость и по уравнению (8.5).

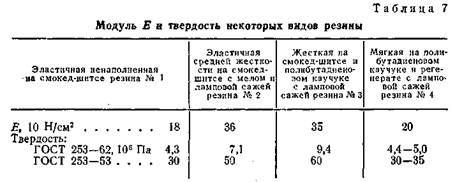
Величины значений Е для некоторых производственных резин приведены в табл. 7.

Данные табл. 7 были получены при исследовании на сжатие образцов резины со смазкой их опорных поверхностей. Исследова­лись шесть видов круговых ре­зиновых цилиндров диаметром 31 мм и высотой от 38 до 5 мм и три вида образцов цилин­дрических резиновых колец наружным диаметром 31 мм, внутренним — 14,7 мм и высо­той от 11 до 5 мм. Сжатие производилось в равноскоростной деформации до Я, в преде­лах 0,90—0,50 с замерами че­рез 1 мин после приложения последовательно возраставшей нагрузки.

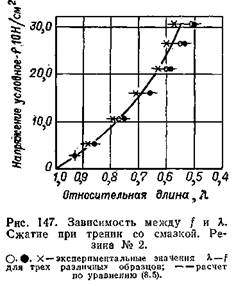
Несмотря на значительное различие габаритов исследо­ванных образцов, ширина пуч­ка зависимости f—л незначи­тельна, и разброс эксперимен­тальных значений, по сравне­нию с рассчитанными по урав­нению (8.5), невелик.

На рис. 147 приведены экспериментальные и расчетные значе­ния л по заданным f для трех различных видов цилиндрических образцов из исследованной серии. Как уже было замечено, явле­ние сжатия при сухом трении более сложно. Цилиндрический об­разец резины, подвергаемый одноосному нагружению между двумя сухими плитами пресса, испытывает (в направлении, перпендику­лярном нагружению) двухосное растяжение, а по плитам и вблизи них, вследствие возникновения трения — сдвиг. Совместный эффект сжатия, двухосного растяжения и сдвига ведет к изгибу (выпучи­ванию) боковой поверхности образца. Вертикальная ось сохраняет свое положение, но лишь при условии ограниченной высоты об­разца, например в отношении h₀: do = 1,5. В образцах большой высоты наблюдается продольный изгиб и образец, теряя устойчи­вость, иногда выскакивает из междуплитного пространства. Наи­большее напряжение растяжения создается в сечении, лежащем посредине высоты образца на его периферии. В центре опорных поверхностей образец частично испытывает трехосное сжатие.

Нахождение расчетной зависимости напряжение — деформация cжатия при сухом трении затрудняется из-за неоднородности распределения нормальных напряжений и возникающего объемного напряжения, связанного с формой и габаритами образца. Исследо­вание распределения нормальных напряжений резины с учетом трения могло бы дать правильное понимание явления, но оно еще недостаточно изучено. В обход этого затруднения, для практиче­ской оценки поведения резины при сжатии, условно заменяют слож­ное напряженное состояние простым сжатием с учетом формы образца.

В качестве условного обобщающего измерителя влияния формы принимают коэффициент формы Ф. Коэффициент Ф понимают как отношение опорной поверхности образца к той или иной части ее, обычно к полной боковой поверхности. Отсюда для круговых ци­линдров Ф имеет следующее значение

где d1 и d₂ — внутренний и наружный диаметры цилиндра; h₀ и b — высота и толщина стенки цилиндра.

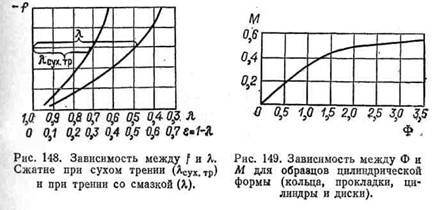
Для решения подобных задач может быть принят такой общий метод. Допускается (рис. 148), что при равных напряжениях f между величиной относительной высоты образца при сжатии в ус­ловиях сухого трения Л_cvx. тр и величиной относительной его вы­соты л при сжатии со смазкой есть достаточно постоянная зависи­мость, выражаемая коэффициентом затрудненности скольжения М;

Этот коэффициент для серии однотипных, но разногабаритных образцов можно найти экспериментально и связать его с коэффи­циентом формы Ф в табличной или графической зависимости.

Из уравнения (8.13) находят относительную высоту л образца, сжимаемого при трении со смаз­кой

Теперь от уравнения (8.5) сжатия при трении со смазкой можно перейти к уравнению сжа­тия при сухом трении. Для этого в уравнении (8.5) достаточно за­менить % ее обозначением из уравнения (8.13′)

На рис. 149 дана зависимость М от Ф для ряда массивных и полых цилинд­ров и дисков с коэффициентом формы 0,20—3,25.

Как видно из рис. 149, зависимость М от Ф нелинейна и отвечает двум кри­вым, переходящим одна в другую при Ф = 1,35, Эти кривые достаточно близко описываются следующими уравнениями:

Графическое сопоставление расчетных и экспериментальных значений Л_сух. тр по заданным напряжениям f для двух видов об­разцов дано на рис. 150. Для круговых цилиндров из ненаполненной резины при сжатии без смазки линейность зависимости о и е приводит к следующему уравнению;

где Есж.к — условно принимаемый модуль сжатия конструкции по истинному напряжению, зависящий, как и статический модуль сжа­тия Е резины, от характера деформации, а также от габаритов образца и условий на опорных поверхностях; а — постоянная, зависящая от трения по опорным поверхностям.

Здесь а приближенно равна удвоенному коэффициенту трения М_T резины по металлу, из которого изготовлены сжимающие плиты; удвоение М_T отвечает количеству трущихся пар.

При наличии надлежащей смазки, когда а может быть при­нята близкой к нулю, Е_сж._к независимо от величины Ф становится равным Е. С увеличением Ф значительно возрастает и Есж.к. Для случая прочного крепления опорных поверхностей образца резины к металлическим прокладкам а, независимо от коэффициента Ф, может быть принято равным 4,67. Наличие «выкружки» по боко­вой поверхности может вести к устранению бочкообразности.

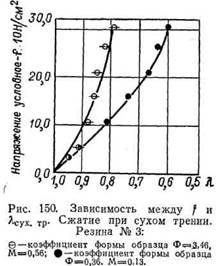
При постоянстве Ф уравнение (8.16) показывает возможность моделирования: точки зависимости f и е для геометрически подоб­ных образцов из одной и той же резины хорошо ложатся на одну кривую (рис. 151). Однако при значительных деформациях, или для образцов больших размеров, или же сложных конфигура­ций, названные зависимости недостаточны.

В зависимости от особенностей формы, наличия отверстий или ребер в резиновых пластинах жесткость их, являющаяся очень важной технической характеристикой, может быть различной.

На рис. 152 приведена зависимость между условным напряжс нием сжатия f и относительным сжатием (осадкой) е для пластин, имеющих одинаковые опорные поверхности, но различную тол щину (высоту). По мере увеличения толщины (иначе — с уменьше­нием коэффициента формы) относительное сжатие возрастает, жесткость уменьшается, резиновая пластина становится «мягче». При наличии отверстий или пор в пластинах это сказывается более значительно (кривая 5 на рис. 152). С уменьшением же толщины пластина становится жестче. Применение смазки, нивелируя влияние коэффициента формы Ф, приводит к объемлющей кривой, лежащей ниже кривой 4 (а возможно и кривой 5).

Примером резиновых изделий, работающих на сжатие, являют­ся уплотнительные прокладки и амортизаторы.

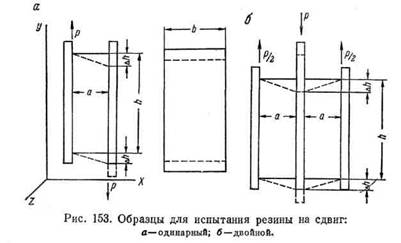
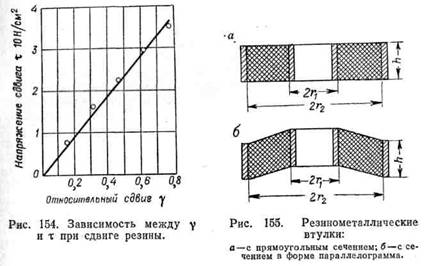
Сдвиг. В практических условиях работы резины при так назы­ваемом простом (плоском) сдвиге (рис. 153, а) напряжение сдвига т приложено на двух параллельных сторонах образца резины, к ко­торым привулканизована металлическая арматура. Отношение смещения Аh к начальной толщине образца а представляет собой относительный сдвиг у. Поскольку площадь плоскости сдвига по­стоянна, понятия условного и истинного напряжений сдвига т со­впадают. Материальной константой зависимости т и у является модуль сдвига G, зависящий от характера деформации резины

Графическая зависимость т и у (рис. 154) при деформации сдвига малонаполненных резин до у порядка 0,7—0,8 практически линейна. Осевое растяжение может заметно сказаться и осложнить эту зависимость в том случае, если размер а превышает 0,25 h₀. При сдвиге в образце одновременно проявляются: растяжение по одной из диагоналей и сжатие по другой. При этом относительные деформации диагоналей е меньше относительного сдвига у. Кроме напряжения сдвига т резиновый блок испытывает и нор­мальное напряжение растяжения по оси у (рис. 153):

Это нормальное напряжение, будучи пропорциональным квад­рату относительного сдвига, незначительно лишь тогда, когда сдвиг мал, но становится существенным при его большой величине. По оси z нормальное напряжение может быть принято равным нулю. В конструкциях цилиндрических резиновых втулок (рис. 155) пло­ский сдвиг обращается в круговой. Напряжение в круговом сдвиге прямоугольной резиновой втулки при малой деформации:

Максимальное его значение отвечает внутренней поверхности резинового массива. Осевое смещение Ah в круговом сдвиге состав­ляет:

Для конструктора, относящего расчетные напряжения к началь­ным площадям нагружаемых сечений, важно относительное по­стоянство модуля сдвига G, по сравнению с переменным и возрастающим дифференциальным модулем сжатия Ef. Суще­ственно также и то, что модуль сдвига втрое ниже модуля сжатия. Размеры и формы монолитных образцов резины, прочно (полно­стью) прикрепленных к металлической базе, практически не влияют на модуль сдвига конструкции, тогда как габариты и вид образцов, работающих на сжатие, значительно сказываются на модуле сжа­тия конструкции.

Модуль сдвига в приближенной зависимости от твердости ре­зины характеризуется следующими данными:

Практические пределы G для производственных резин состав­ляют (3,5—20) -10 Н/см 2 .

На сдвиг работают многие резиновые конструкции, в частности пластинчатые амортизаторы. Максимально допустимое т состав­ляет (3,9—4,2)-10 Н/см 2 , а в тяжелых условиях дина­мических режимов даже (2,1— 2,4). 10 Н/см 2 , а макси­мальное у не должно пре­вышать 0,5.

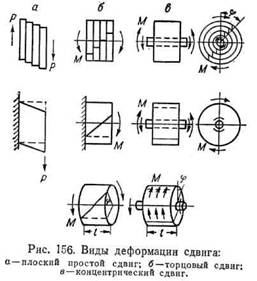
Кручение. Различают два вида скручивания резины: торцовое и концентрическое. Эти виды кручения можно рассматривать как явление торцового и концентриче­ского сдвигов. Последний наблюдается в резиновых втулках (рис. 156), заключенных между двумя метал­лическими деталями (так называемых бесшумных блоках).

Расчетная зависимость полного углового смещения ф в радианах и крутящего момента М торцового кручения при ма­лых деформациях определяется уравнением

В случае рассматриваемого торцового кручения резины, кроме Касательного напряжения т, имеется нормальное f_z по свободной торцовой поверхности (по оси z). Это нормальное напряжение цвисит от квадрата величины углового смещения ф/l, неоднородно и распределено по торцовой поверхности по параболическому за­кону:

Угловое смещение при концентрическом кручении цилиндриче­ских резиновых прямоугольных втулок при малых деформациях определяется следующим уравнением:

и достигает максимума по внутренней поверхности втулки. Пример резиновых изделий, работающих на кручение, — демпфер крутиль­ных колебаний коленчатого вала.

Изгиб. При значительном изгибе гибких металлических дета­лей— тонких полос и стержней, имеющих (вследствие малой вели­чины их момента инерции I) малую изгибную жесткость EI,— неприменимо известное упрощенное уравнение упругой линии:

Для этого случая Е. П. Поповым подробно разработана теория изгиба, позволяющая вести расчет брусьев малой жесткости в случае любых больших прогибов и перемещений точки приложе­ния нагрузки. Для практического применения общих решений этой теории им дан графоаналитический метод расчета по диаграммам упругих параметров и таблицам для построения этих диаграмм.

Теория расчета изгиба при больших перемещениях представляет интерес и для исследования изгиба резиновых и резино-текстильных слойных конструкций. В этих случаях, вследствие малой неличины модуля Е, условная жесткость их EI также мала. Такие изделия могут иметь значительный прогиб, а при консольном нагружении их также и со значительным смещением точки приложения нагрузки.

Исходя из таблиц и уравнений упругих параметров Е. П. Попова, могут быть даны графические построения для расчета эффективного модуля изгиба таких конструкций в частных задачах, соответствующих нагружению консоли и кольца.

Кривая 1 рис. 157, соответствующая нагружению по приведен­ной на рисунке схеме, позволяет по экспериментально определен­ному отношению прогиба консоли у к длине I найти величину в, так называемый силовой коэффициент подобия. Зная в, можно по заданным нагрузке Р, длине l и моменту инерции I из уравнения

вычислить Е_из— материальную характеристику изгибоспособноети конструкции (эффективный модуль при изгибе) и условную при изгибе жесткость конструкции Еиз1 (принимая ее в пределах экспери­мента постоянной).

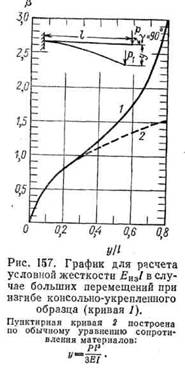
Кривая 1 рис. 158, отвечающая нагружению по приведенной на рисунке схеме, позволяет найти в как функцию отношения y/R. Аналогично уравнению (8.27), но заменив в нем l на R, а Р на 0,5 Р, можно найти Е_из. Пунктирные линии на рис. 157 и 158 соот­ветствуют зависимости, вытекающей из обычных уравнений сопро­тивления материалов. Нагружение по схеме изгиба консоли рис. 157 удобно для исследования изгиба резино-текстильных пла­стин. По схеме рис. 158 ведут исследования радиального прогиба резины, имеющей форму кольца прямоугольного сечения среднего радиуса R, или резино-текстильной полоски, свертываемой в такое кольцо. Если применяется схема рис. 158, El следует заменять ци­линдрической жесткостью:

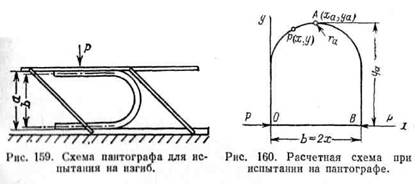
Метод экспериментального определения жесткости при изгибе, удобно при­менимый для резино-текстильных изделий (плоских и клиновых ремней, рукавов, технической пластины), предложен Штекертом. Прямой участок испытывае­мого изделия изгибают U-образно по схеме рис. 159 в приспособлении, состоя­щем из двух параллельных планок пантографа. Усилие Р (в ЮН) и расстояния а (в см) измеряют; расстояние между ней­тральными поверхностями Ь (в см) рассчи­тывают, исходя из геометрических размеров поперечного сечения исследуемого изделия. Из теоретических положений, следуя схеме обозначений на рис. 160, Штекертом найдены следующие зависимости:

Следует доводить изгиб до кривизны, отвечающей условиям эксплуатации, так как жесткость El зависит от величины изгиба изделия. Замеры следует про­изводить через определенные промежутки времени после приложения нагрузки, например через 30 с. Перегибать изделия до «залома» не следует.

Сложные виды деформаций. Основные виды деформации — растяжение, сжатие, сдвиг и кручение — в реальных конструкциях резиновых деталей осложняются взаимным наложением в различ­ных комбинациях, что приводит к сложным видам деформаций, например вдавливанию. Обычно сжатие сопровождается сдвигом, а иногда — кручением. Результат комбинированных нагружений выражается в изменении характера кривых на диаграммах зави­симости условное напряжение — деформация конструкции. В от­дельных случаях зависимость принимает линейный характер. Од­нако необходимо учитывать, что отношение напряжения к дефор­мации в линейной их зависимости представляет собой модуль лишь при упругой деформации. Условием этого можно считать, что деформации при последующей разгрузке вполне или в значи­тельной степени, например на 90—95%, обратимы.

Двухосное растяжение резины, являющееся аналогом чистого одноосного сжатия, было предметом ряда исследований . Модуль резины при двухосном растяжении для равновесной деформации, при растяжении 10—100%, в 1,57 раза выше модуля одноосного растяжения. Случай чистого двухосного сжа­тия не исследован. Более доступен для изучения относительно близкий к нему случай одноосного удлинения резины, сжимаемой в канале заданной ширины. Поскольку при такой деформации значительно проявляется объемное напряжение, коэффициент за­трудненности скольжения М получает иное значение, зависящее от габаритов и конфигурации канала и длины образца.

Трехосное растяжение резины практически неосуществимо; тео­ретически такой случай близок к свободному набуханию резины в подходящей жидкости. Трехосное сжатие, например, представ­ляет собой случай осевого нагружения резиновой прокладки в же­стком гнезде с размерами, равными наружным размерам образца. В подобных условиях резина, не имея возможности деформации по двум остальным осям, ведет себя как малосжимаемый материал. Модуль резины при трехосном сжатии, или так называемый объем­ный модуль, весьма значителен [около (2,7—3,8) -10 Н/см 2 ].

Усталость резины. В зависимости от особенностей назна­чения резиновые детали подвергаются различным условиям дли­тельного нагружения. Длительное приложение нагрузки ведет к усталости материала. Способность материала сопротивляться усталости — выносливость — может быть определена длительностью в зависимости от величины нагружения и величины деформации. Применение длительных статических нагрузок встречается при ис­пользовании резины в качестве уплотнительных прокладок в не­подвижных узлах. Находящийся в длительном статическом нагру-жении постоянным грузом (даже значительно меньшим «мгно­венно» разрушающего) образец резины все же разорвется. Разрыв наступит за время, тем более короткое, чем больше нагружен обра­зец. Эта статическая усталость проявляется как в массе исследуе­мого образца резины, так и в тонком слое, соединяющем, напри­мер, резину с металлической арматурой. Ближайшей причиной разрушения при статической усталости, как уже указывалось, яв­ляется наличие в материале беспорядочно размещенных относи­тельно слабых мест и надрывов, вызывающих концентрацию на­пряжений или связанных с значительными местными отклонениями в свойствах материала.

Резина, по сравнению со сталью, способна вынести деформации во много раз больше, так как пределы (хотя и несовершенной) уп­ругости и прочности резины практически совпадают. При этом, если рабочие деформации растяжения не превышают 10% от деформа­ций, происходящих при разрушении образца, то после прекращения действия деформирующих усилий образец резины почти полностью возвращается в исходное состояние и принимает свои прежние раз­меры.

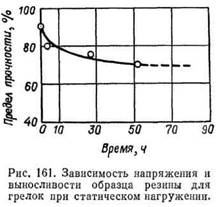
Разрыв под влиянием статической усталости иногда происхо­дит внезапно, без предшествующего указания на близкое разруше­ние. Зависимость приложенного условного напряжения и длитель­ность сопротивления разрыву следуют кривой, асимптотически приближающейся к оси абсцисс. Разные типы резины при испыта­нии в одинаковых условиях дают различные результаты. Пре­дельно допустимым в рассмотренном нами случае (рис. 161) (ре­зина для грелок) является для f 70% от предела прочности резины на разрыв. В логарифмических координатах эта зависимость ли­нейна. Чаще, однако, резина работает в периодических, динами­ческих (шины, амортизаторы, уплотнители подвижных узлов) или ударных (буферы) режимах нагружения.

Динамические режимы могут быть различны по виду нагруз­ки (циклическая, переменная, пульсирующая и др.) и по частоте, а следовательно, различны и по длительности приложения нагруз­ки. В том случае, когда эта дли­тельность приближается ко вре­мени, необходимому для релак­сации напряжения, последнее, замеряемое в конце цикла дефор­мации, близко к равновесному. Чем меньше длительность прило­жения нагрузки, тем замеряемое напряжение ближе к начально приложенному. Сопротивление резины динамическому утомле­нию (проявлению динамиче­ской усталости) зависит от потерь на внутреннее трение. При значительном напряжении в этом сопротивлении преобладает физический фактор — прочность резины. При малом напряжении и отвечающей ему длительности сопротивления существенное зна­чение имеет химическая стойкость резины. Уменьшение внутрен­него трения, наблюдающееся, например, при набухании, снижает интенсивность хода химических реакций и ведет к увеличению динамического сопротивления.

Выносливость к многократным деформациям резиновых изде­лий зависит не только от вида резины и характера деформаций, но в большей степени от размеров и конфигурации деталей, а также от характера цикла (т. е. от условий нагружения). Предел усталости в знакопостоянном цикле меньше, чем в знакоперемен­ном (ср. 2 и 1 на рис. 109). Отсюда усталостное поведение резины в образцах в условиях лабораторных испытаний нельзя, безотно­сительно к конкретным условиям работы изделий, распространять на поведение резины в эксплуатации.

При расчетах резины в динамических циклах рекомендации сво­дятся главным образом к установлению эмпирической зависимости между напряжением или деформацией и количеством циклов де­формации, перенесенных образцом до разрушения или до опреде­ленной величины потери начальных прочностных свойств. Более широко применяются расчеты резины как виброизолирующего средства.