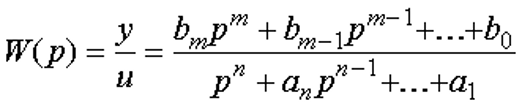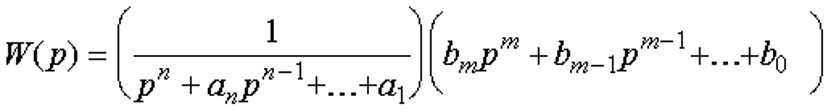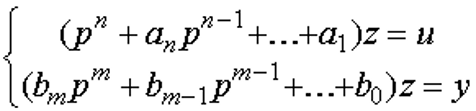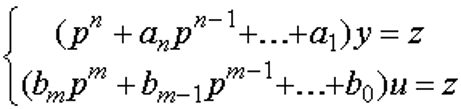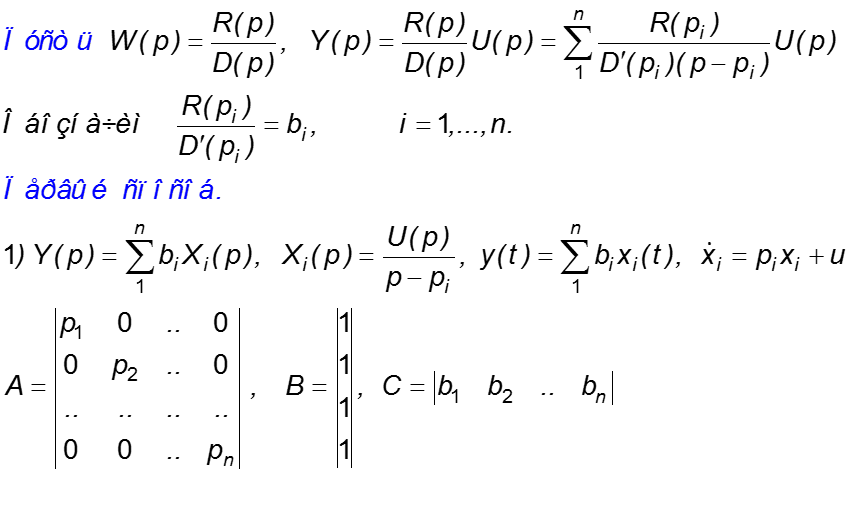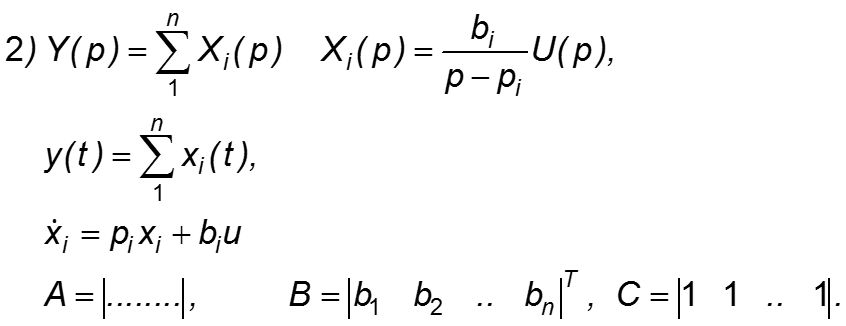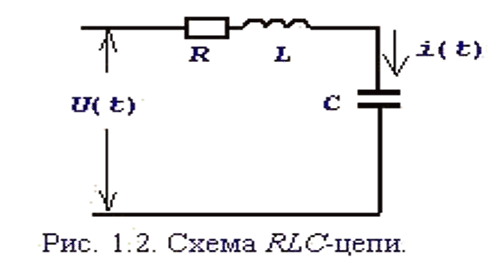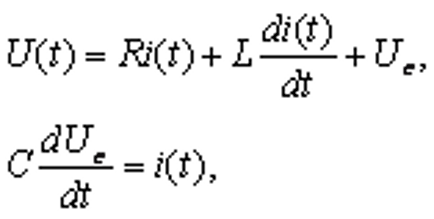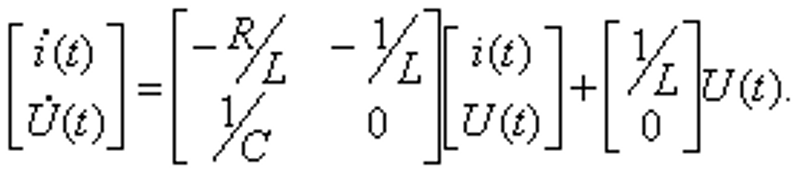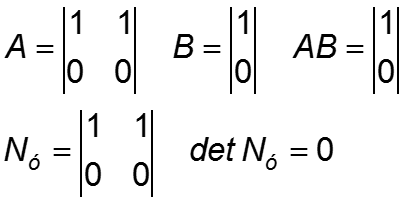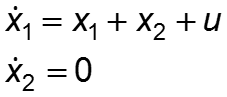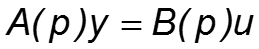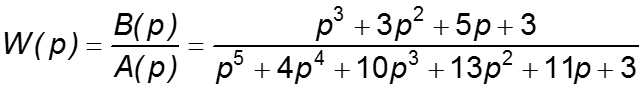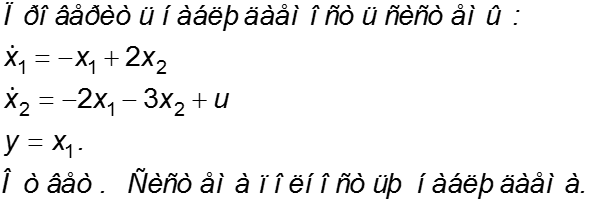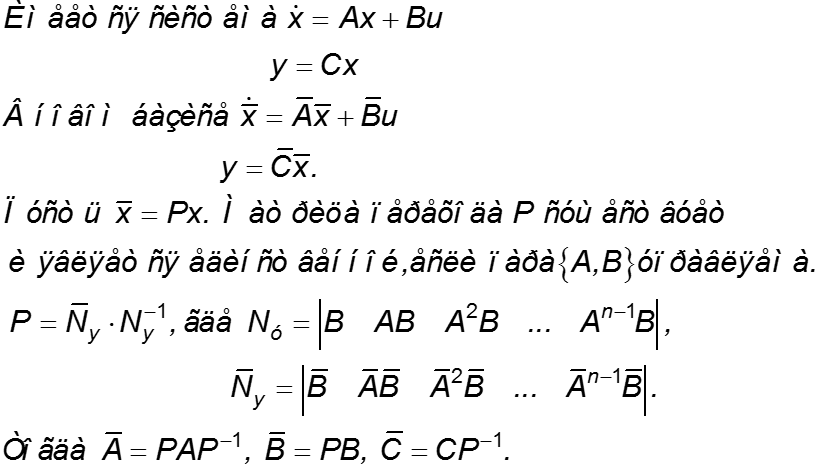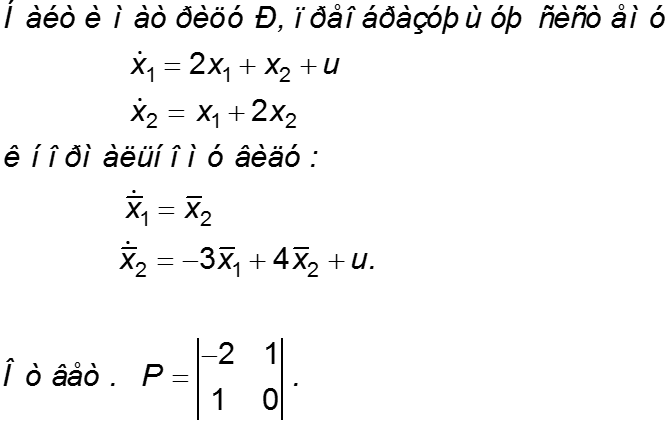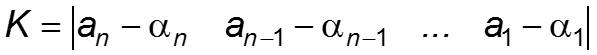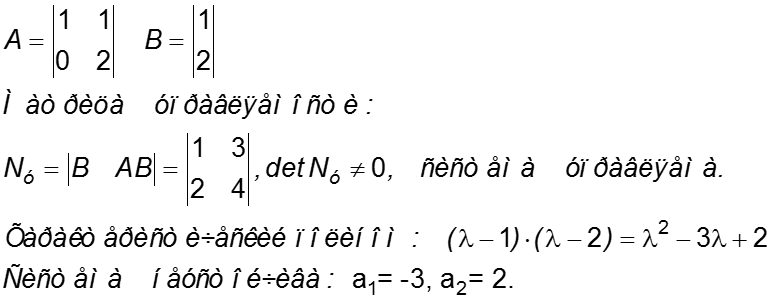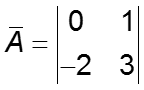Уравнение состояния системы в нормальной форме

Уравнения состояния

При решении некоторых задач теории автоматического управления удобнее представлять дифференциальное уравнение объекта (5.1) или дифференциальные уравнения системы (5.4) и (5.6) в виде совокупности дифференциальных уравнений первого порядка. Не умаляя общности, рассмотрим эти уравнения применительно к управляемому объекту.

Пусть объект описывается дифференциальным уравнением n-го порядка (5.1)

называемых переменными состояния и представим уравнение (5.70) в виде системы дифференциальных уравнений

устанавливается алгебраическим уравнением

Обычно уравнения (5.71) и (5.72) записываются в векторпо-матричной форме:

— матрицы-столбцы. Матрицу-столбец-

могут иметь неодинаковые размерности.

В выборе переменных состояния имеется определенная свобода. Важно только, чтобы они были независимыми. От того, как выбраны переменные, зависит форма уравнений (5.73) и (5.74), т. е. вид входящих в них матриц.

При нормальной форме уравнений состояния в качестве переменных состояния выбираются сама управляемая величина \п- 1 ее производные:

т. с. когда оно имеет вид

Достоинством нормальной формы является то, что переменные состояния имеют ясный физический смысл, а некоторые из них (например, хих2 и х:]) могут быть непосредственно измерены датчиками различных типов.

Для получения уравнений состояния в канонической форме уравнение объекта (5.70) представляется в виде

Если корни рь Ръ-Рп полинома С0(р) действительные однократные, то правая часть (5.80) может быть представлена в виде суммы элементарных дробей:

где К; и ()г- — коэффициенты разложения.

В качестве неременных состояния выбираются слагаемые суммы (5.81):

Большим достоинством канонической формы является диагоиальиость матрицы Л , что существенно упрощает решение уравнения (5.73). Основной недостаток ее состоит в том, что переменные состояния не имеют ясного физического смысла, в результате чего возникает проблема их непосредственного измерения.

Существуют и другие способы выбора переменных состояния, которые здесь не рассматриваются.

Решение векторно-матричиого уравнения (5.73) может быть представлено в виде

Здесь оно без строгого доказательства построено по аналогии с решением линейного дифференциального уравнения 1-го порядка

общий интеграл которого, как известно, определяется но формуле

называется переходной или фундаментальной матрицей. Если уравнения состояния представлены в канонической форме, то матрица А диагональная и имеет вид (5.85). Тогда

При других формах уравнений состояния для определения фундаментальной матрицы можно использовать известные способы нахождения матричных функций, например, теоремы Кели—Гамильтона или Сильвестра. Можно также использовать формулу

—

При необходимости можно осуществить обратный переход от уравнений состояния к передаточным функциям объекта. Для этого уравнение (5.73) запишем в изображениях по Лапласу:

получается формула (5.88). Из уравнения

(5.74) с учетом (5.89) найдем изображение управляемой величины при нулевых начальных значениях:

При описании свойств объекта уравнениями состояния возникают две проблемы, нетипичные для случая, когда используется одно дифференциальное уравнение я-то порядка. Эти проблемы рассматриваются в следующем параграфе.

Уравнение состояния системы в нормальной форме

СОСТАВЛЕНИЕ ДСС ПО ПЕРЕДАТОЧНОЙ ФУНКЦИИ

Схема системы в переменных состояния может быть составлена по передаточной функции тремя способами: методом прямого программирования, методом параллельного программирования и методом последовательно программирования.

Метод прямого программирования

Этот метод позволяет представить систему уравнений состояния в нормальной канонической форме по известной передаточной функции звена или системы с одним входом и одним выходом.

Известно, что системе с передаточной функцией

соответствует дифференциальное уравнение

где P i = d i / dt i

Рассмотрим вначале систему с передаточной функцией

которой соответствует дифференциальное уравнение

Введем обозначения: y 1 = x 1 и при i=1, 2, . n-1. и запишем последнее уравнение в виде

Следовательно, система уравнений состояния, соответствующая передаточной функции (4.1) , м.б. записана в виде

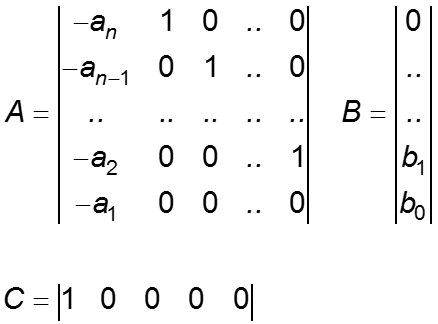
Записывая эту систему в векторно -матричной форме, получим

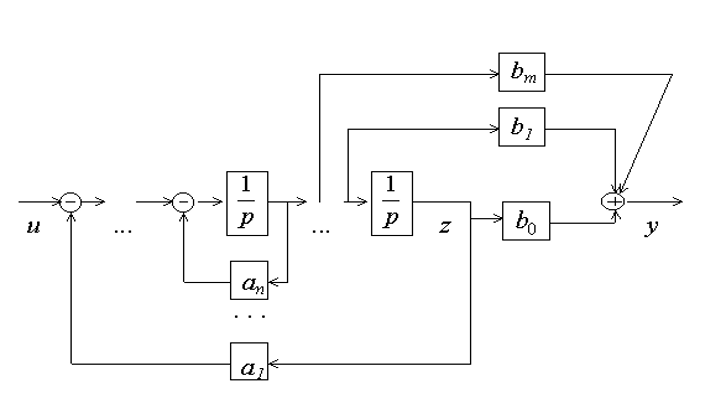
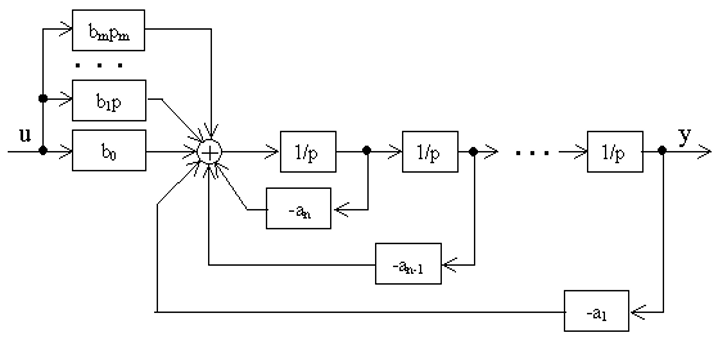
Используя уже известные правила, построим Д C С по уравнениям состояния в виде рис. 4.1. :

Рассмотрим теперь систему с передаточной функцией

которой соответствует дифференциальное уравнение

Подстановкой x 1 =x 2 / b 0 уравнение ( 4.4 ) сводится к ( 4.2 ) и следовательно ,

— уравнения состояния, соответствующие передаточным функциям (4.1) и (4.3) разнятся только масштабом выходной переменной и, следовательно, только элементами матрицы С . Для последнего случая

— в ДСС появляется дополнительное масштабирующее звено с коэффициентом передачи b 0 , со входом y 1 и выходом x 2 . Это звено выделено жирной штриховой линией на рис. 4.1.

Рассмотрим далее систему с передаточной функцией

Этой передаточной функции соответствует дифференциальное уравнение

Выходную величину X i можно представить в операторной форме выражением

Переходя к функции времени, получим

Следовательно, ДСС данной системы с передаточной функцией (4.5) может быть получена из ДСС уже известной системы путем введения масштабирующего звена с коэффициентом передачи b i , входом y i+1 и выходом x i. В уравнениях состояния изменятся лишь элементы матрицы С . Последняя будет иметь вид

Таким образом выходную величину исходной системы с передаточной функцией

можно представить в виде суммы в соответствии с числом слагаемых полинома числителя M(p), т.е.

Переходя к функции времени, получим

или с учетом ранее введенных обозначений

Следовательно, структурная схема исходной системы отличается от ранее полученных наличием полного набора масштабирующих звеньев ( всего их m+1 ) c коэффициентами передачи b i в цепи формирования выходной переменной x. (см. рис. 4.1.)

Матрицы А и В всех рассмотренных систем одинаковы. Их элементы формируются из коэффициентов полинома знаменателя передаточной функции.

Коэффициенты полинома числителя определяют только элементы матрицы С и влияют лишь на формирование выходной переменной. В последнем наиболее общем случае матрица С имеет вид

Пример1: Составить ДСС и систему уравнений состояния для звена с передаточной функцией

Приведем передаточную функцию звена к стандартному виду

где a 0 =1/T 2 , b 0 =1/T 2 , b 1 =T 1 /T 2

Стандартной передаточной функции соответствует стандартная ДСС:

и система уравнений состояния первого порядка

Рассмотрим еще пример:

Составить ДСС и уравнения состояния для системы, заданной передаточной функцией

Приводя запись передаточной функции в стандартную форму, получим: a 2 =7, a 1 =12, a 0 =0, b 2 =1, b 1 =3, b 0 =2.

ДСС изобразим в стандартном виде

Система уравнений состояния для этого случая в обычной форме

В матричной форме

При указанном подходе передаточная функция исходной системы представляется в виде суммы передаточных функций однотипных звеньев следующим образом:

Здесь l i -корни полинома знаменателя передаточной функции, а a i — находятся по формуле

Такая передаточная функция соответствует параллельному соединению n однотипных звеньев со структурными схемами, представленными на рис. 4.4 .

Выходные сигналы x i звеньев суммируются .

Используя эту методику, составим ДСС для рассмотренной выше системы. Корни знаменателя равны : l 1 =0, l 2 =-3, l 3 =-4.

Вычисляя коэффициенты числителей, получим a 1 =1/6, a 2 =-2/3, a 3 =3/2. Тогда структурная схема системы примет вид (рис.4.5.)

Этой структурной схеме соответствует следующая система уравнений состояния

Для составления ДСС этим методом исходная передаточная функция представляется в виде произведения дробно-рациональных функций, порядок полиномов знаменателя и числителя которых не превышает единицы. Если порядки числителя и знаменателя исходной передаточной функции одинаковы, т.е. m=n, то последняя записывается в виде

где b k и l k — соответственно корни полинома числителя (нули) и корни полинома знаменателя (полюса). Если n>m (что практически всегда имеет место), то (n-m) сомножителей имеют в числителе единицу. Стандартная ДСС для элементарной дробно-рациональной функции общего вида нами была ранее, по существу, обоснована. Она изображается в виде

Поскольку произведение передаточных функций соответствует последовательному соединению звеньев, ДСС исходной системы будет содержать n последовательно соединенных ДСС идентичной конфигурации.

Передаточную функцию уже рассмотренной системы представим в виде произведения трех дробей

ДСС соответствует последовательному соединению ДСС элементарных звеньев и имеет следующий вид

Этой ДСС соответствует следующая система уравнений состояния

в матричной форме принимающая следующий вид

Следует подчеркнуть, что для одной и той же системы можно составить несколько схем в переменных состояния, отличающихся природой промежуточных переменных, выбранных для описания системы. Различному выбору переменных состояния соответствуют различные матрицы системы, управления и наблюдения и различные векторные дифференциальные уравнения.

Методы переменных состояния в теории автоматического управления. Современная теория автоматического управления

Страницы работы

Фрагмент текста работы

Характеристическое уравнение располагается в последней строке.

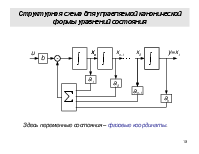
Структурная схема для управляемой канонической формы уравнений состояния

Здесь переменные состояния – фазовые координаты.

Другая форма: в правой части уравнения содержатся производные от входного воздействия

Введем переменные состояния:

Здесь координаты состояния xi – абстрактные переменные.

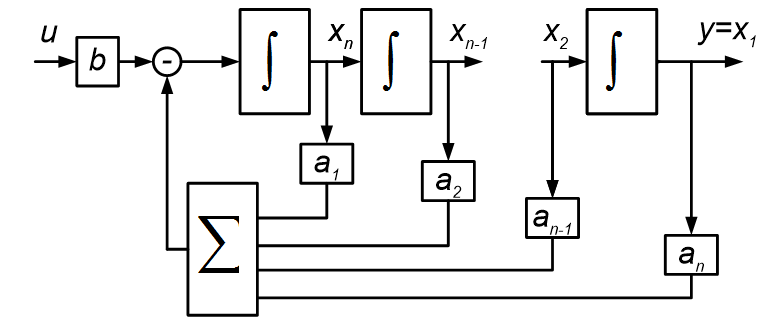
Этим уравнениям соответствует структура:

Возможно другое представление:

Структурная схема может быть преобразована к виду:

Тогда матрицы A, B, C в уравнениях состояния будут:

Это — наблюдаемая каноническая форма уравнений состояния.

Таким образом, переход от передаточной функции к описанию в переменных состояния является неоднозначным.

Другие канонические формы уравнений состояния.

В двух последних формах матрица А – диагональная.

• Преимущества структурной модели :
• наглядное представление понятия «состояние систем»,
• однозначно представляется структура взаимодействий
• между переменными в виде системы с обратными связями,
• структурные модели полезны при моделировании САУ
• на аналоговых или цифровых вычислительных машинах.

Пример получения уравнений состояния

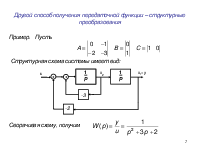
П р и м е р. Система описывается дифференциальным уравнением Составим уравнения состояния и структурную схему

Свойства объектов и систем управления. Управляемость .

Определение. Система полностью управляема, если она может быть переведена из любого начального состояния x(0) в начало координат (0, 0,…,0) под действием управления u(t) за конечное время. Теорема Калмана об управляемости. Состояние непрерывной системы управляемо, если и только если ранг матрицы NУ = [B | AB | A2B | . | An-1B] равен размерности пространства состояний n.

Пример 1. Проверим, управляема ли система:

Пример 2. Также проверим управляемость системы:

Т.к. rangNy = 1 , система управляема неполностью. Порядок управляемой части равен 1.

В такой системе есть “висячая” часть на входе.

В случае представления объекта управления моделью типа “вход — выход” условием его управляемости является отсутствие общих корней полиномов А(p) и B(p): Т.е. система управляема, если алгебраические уравнения A(p)=a0pn+a1pn-1+…+an = 0, B(p)=b0pm+b1pm-1+…+bm = 0 не имеют общих корней.

Пример 2. Определим управляемость системы, имеющей передаточную функцию

Прямой расчет корней числителя и знаменателя дает результаты, приведенные в табл.

Таким образом, числитель и знаменатель передаточной функции W(p) имеют два общих корня (-1 -j1.414) и ( -1+j 1.414). Значит, система не управляема. Изменение значений корней для этих пар в числителе или знаменателе переведет систему в ранг управляемых.

• Для осуществления управления необходимо иметь информацию о текущем состоянии системы, т.е. о значениях вектора состояния x(t) в каждый момент времени.
• Однако некоторые из переменных состояния являются абстрактными, не имеют физических аналогов в реальной системе или же не могут быть измерены. Измеряемыми и наблюдаемыми являются физические выходные переменные y(t).
• Таким образом, возникает вопрос: можно ли определить вектор состояния по измеряемому вектору выхода и вектору входа?

• Определение. Система называется полностью наблюдаемой, если по результатам измерения входных u(t) и выходных y(t) переменных можно однозначно определить все составляющие вектора x(t) на конечном интервале времени.
• Теорема Калмана о наблюдаемости. Система наблюдаема, если и только если ранг матрицы
• Nн = [CT | ATCT | (AT)2CT | . | (AT)n-1CT].
• равен размерности пространства состояний.

Изменение базиса в уравнениях состояния

О синтезе системы

• Синтез системы — это направленный расчет, цель
• которого :
• построение рациональной структуры системы;
• нахождение оптимальных значений параметров отдельных звеньев.
• Качество управления можно описать двумя способами.
• Первый способ предусматривает или непосредственное задание динамических характеристик выходных координат системы при типовых воздействиях, или задание совокупности прямых и косвенных показателей качества (значение перерегулирования, времени регулирования, статической ошибки, частоты среза, полосы пропускания и т.д.).
• Второй способ основан на введении некоторого обобщенного функционала, определяемого всеми переменными системы управления u(t), x(t), y(t).
• В теории линейных систем управления широко используются оба указанных способа.

• Если передаточная функция системы не имеет нулей, то при выборе ее желаемого полинома D(p) можно руководствоваться стандартными формами (фильтрамиЧебышева, Баттерворта и др.)
• Стандартные формы определяют коэффициенты характеристического полинома , обеспечивающие в системе переходные и частотные характеристики с известными показателями качества.
• Если же система характеризуется наличием нулей, стандартные формы могут служить в качестве исходного материала для поиска своего оптимального расположения корней.
• Одним из основных методов проектирования детерминированных систем управления в пространстве состояний является метод расположения полюсов.

Распределение полюсов системы управления

• Рассмотрим систему с одним входом и одним выходом.
• Требуемое качество процессов может быть достигнуто заданием распределения полюсов замкнутой системы на комплексной плоскости.
• Для системы
• полюса системы — это собственные значения матрицы А или корни ее характеристического уравнения

• Если уравнения объекта заданы в нормальной форме (Фробениуса), то матрица обратных связей по состоянию
• Покажем это:

Нормальная форма матрицы А:

Пусть желаемые полюсы : λ1= -3, λ2= -2 Желаемый характеристический полином: φ=(λ+3)(λ+1)= λ 2+4 λ +3; α1=4, α2=3. Тогда k1 = a2 — α2 = 2 — 3 = -1, k2 = a1- α1 = -3 — 4 = -7. K = |-1 -7| Следовательно: v = u — x1 -7×2 Вычислив матрицу перехода P от исходной к нормальной форме можно получить матрицу обратной связи для исходного представления