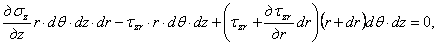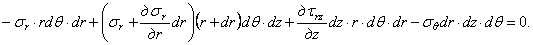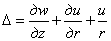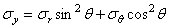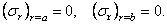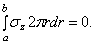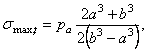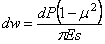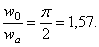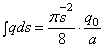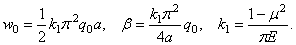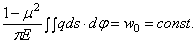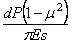Уравнение совместности деформаций в цилиндрических координатах

Лекция 2. Простейшие осесимметричные задачи

2.1 Уравнения в цилиндрических координатах

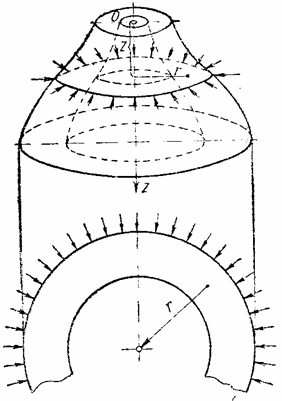
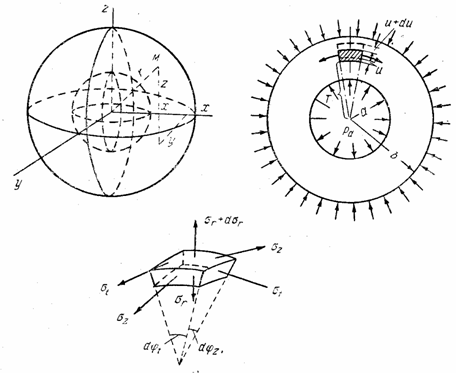
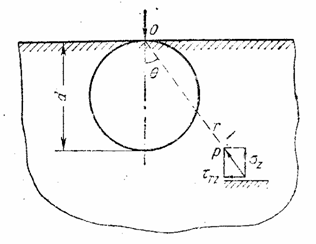
Представим тело вращения, к которому приложены силы, расположенные симметрично относительно оси этого тела (рис.18). Примерами могут быть круглый цилиндр, усеченный конус, деформирующийся под действием равномерного вну­треннего или наружного давления или сил, равномерно приложенных по торцевым сечениям.

За ось вращения примем ось z , ось же перпендикулярную к ней, обозначим через r . Двух координат z и r вполне достаточно, так как все точки с одинаковыми такими коор­динатами находятся в одинаковых условиях.

Так как каждая меридиональная плоскость z 0 r представляет плос­кость симметрии как в отношении формы, так и в отношении нагрузки тела, то в меридиональных плоско­стях касательных напряжений быть не может. Поэтому для каждой точ­ки тела, расположенной на меридиональной плоскости, площадка, содержащая эту точку, является главной площадкой рассматриваемого напряженного состояния. Глав­ное напряжение, действующее по этой площадке, обозначим через .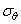

Кроме меридионального сечения через точку с коорди­натами z , r проведем еще второе сечение, перпендикулярное к оси z , и третье сечение, перпендикулярное к двум первым. Следы этих двух секущих плоскостей на меридиональ­ной плоскости будут параллельны соответственно осям r и z .

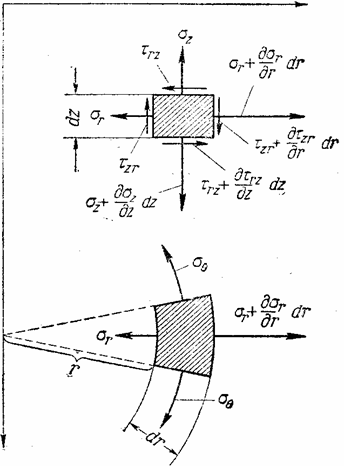
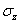
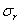
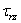
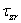
Вследствие симметрии в обеих секущих плоскостях, в точке z , r могут действо­вать лишь такие касательные напряжения, которые парал­лельны меридиональной плос­кости (рис. 19). Нормаль­ные напряжения, действующие в секущих плоскостях, обоз­начим через и , касатель­ные — через и . Эти на­пряжения надо считать функциями от z и r .

Указанные выше условия задачи характеризуют случай, когда основные уравнения упругого равновесия можно представить в такой же про­стой форме, как и в случае плоской задачи, и потому мо­жем ограничиться рассмотре­нием соотношений, имеющих место для точек одной и той же плоскости.

z

Проектируя все усилия, принадлежащие элементарному объему на оси z и r , имеем уравнения равновесия в виде:

После сокращения на общий множитель 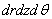статические уравнения запишутся:

(2.1)

Обозначая упругие перемещения точки в направлении оси z через w , в направлении радиуса через и ( в тангенциальном направлении перемещение отсутствует), геометрические уравнения для данного случая можем представить в виде

. (2.2)

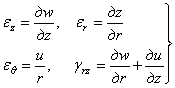
Наконец, физические уравнения, согласно (1.24)

. (2.3)

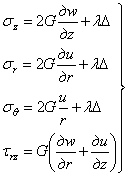
При решении задачи в перемещениях объемное расширение

может быть переписано в виде

, (2.4)

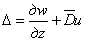
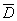
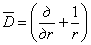
где под надо понимать обозначение следующей операции:

.

Подставляя (2.4) в физические уравнения (2.3), и, далее, в уравнения равновесия (2.1), придаем последним вид

(2.5)

. (2.6)

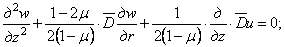
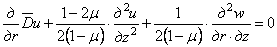
Таким образом, задача определения напряжений в теле вращения, загруженном симметрично относительно оси, сво­дится к нахождению двух функций w и и , которые должны удовлетворять в каждой точке уравнениям (2.5) и (2.6) и одновременно граничным условиям на поверхности тела.

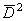
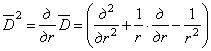
Если, кроме того, ввести оператор , положив

,

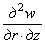
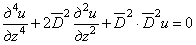
то из уравнений (2.5) и (2.6), исключая из них w , диф­ференцируя (2.5) по z и r и подставляя из (2.6), по­лучим:

. (2.7)

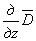
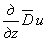
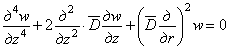
Аналогично можно составить дифференциальное уравнение, которому должно удовлетворять пере­мещение w , если к уравнению (2.6) сначала применить операцию , а затем вставить из уравнения (2.5):

. (2.8)

Установленные уравнения теории упругости в напряжениях (уравнения неразрыв­ности деформаций, выраженные через напряжения), написан­ные в декартовых координатах, можно преобразовать к ци­линдрическим координатам,

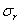
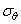
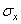
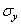
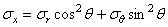
Для этой цели надлежит выразить напряжения и через и по известным формулам перехода

;

заменив запись суммы другой:

,

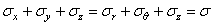
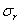
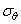
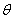
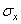
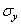
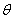
но учесть, что и не зависят от угла , тогда как и являются функциями .

Запишем окончательные резуль­таты для уравнений совместности, которых ввиду осесимметричного характера деформаций останется четыре:

, (2.9)

где введен символ

. (2.10)

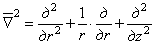
Заметим, что одновременно с уравнениями неразрывности должны быть удовлетворены уравнения равновесия (2.1) и условия на контуре.

Подобно тому, как в плоской задаче теории упругости удалось все компоненты напряжений выразить через одну функцию напряжений, так и в разбираемом осесимметричном пространственном случае имеется такая же возможность.

В самом деле, если задаться

, (2.11)

где — произвольная функция, и подставить (2.11) в первое уравнение равновесия (2.1), то оно обратится в тождество. Второе уравнение равновесия и все уравнения неразрывности будут удовлетворены, если принять согласно уравнению

. (2.12)

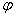
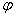
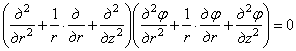
Можно подобрать много решений уравнения (2.12). Вот некоторые из них:

(2.13)

. (2.14)

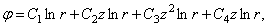
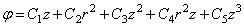
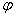
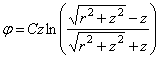
Так как эти выражения удовлетворяют уравнению (2.12) при любых значениях коэффициентов С , следовательно, любой член их также удовлетворяет уравнению (2.12). Например, может быть

. (2.15)

Если в числе прочих причиной, вызывающих напряженное и дефор­мированное состояния тела, является возникновение темпера­турного поля, в общем случае неравномерного вдоль коор­динаты z и вдоль радиуса r , т. е.

то надлежит внести дополнения в физи­ческие уравнения (2.3), а именно, они должны быть запи­саны [(по аналогии с (1.47), но в цилиндрических координа­тах] следующим образом:

(2.16)

(2.17)

(2.18)

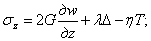
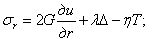
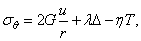
где, введе­но обозначение:

.

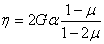
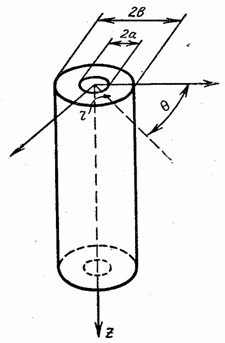
В качестве примера рассмотрим длинную толстостенную трубу (рис. 20) с радиальным перепадом температур, т. е. считается заданным закон Т = Т ( r ).

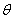
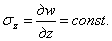
Пренебрегая влиянием торцов, можно считать, что все сечения трубы, перпендикулярные к ее оси, остаются плоскими и все работают в одинаковых условиях. Таким образом, радиальное перемещение u зависит только от r , перемещение v в направлении отсутствует, относительное удлинение по направлению оси z следует считать постоянным, т. е.

(2.19)

Для относительных удлинений в радиальном и тангенциальном направлениях возможно использовать соотношения (1.35,а), (1.35,б) т. е.

. (2.20)

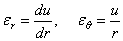
Очевидно в рассматриваемой задаче сохраняется уравнение равновесия из (1.32,б) т.е.

. (2.21)

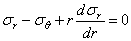
Использование (2.19) (2.20) в (2.16) и (2.18) с последующей подстановкой в (2.21) приводит к разрешающему уравнению следующего вида:

. (2.22)

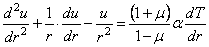
Решением (2.22) является выражение

. (2.23)

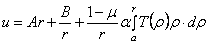
где 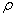— переменная интегрирования.

Далее, очевидно, подлежит подставить (2.23) в (2.17), (2.18), а для определения постоянных А , В и 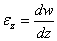использовать граничные уравнения. Так, если внутренняя и наружная поверхности трубы свободны, то, следовательно:

Если труба не имеет осевой нагрузки, то

Приведем окончательные выражения для напряжений на внутренней и наружной поверх­ности трубы для случая, когда на этих поверхностях поддер­живаются постоянные температуры Т _а и Т _b и, следовательно, для такого установившегося потока распределение температур по толщине стенки выражается формулой:

. (2.24)

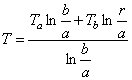
Тогда на внутренней и наружной поверхностях:

(2.25)

. (2.26)

2.2 Деформация толстостенного сферического сосуда

При решении некоторых задач, когда многие компоненты напряжений и деформаций отсутствуют, можно не прибегать к общим уравнениям теории упругости (в пе­ремещениях или в напряжениях), которые должны значительно упроститься, а все три необходимые стороны исследования (геометрическую, физическую и статическую) выполнить непосредственно применительно к рассматривае­мому частному случаю.

Представим себе шаровой сосуд, подвергающийся дей­ствию внутреннего и внешнего равномерных давлений. Пусть а и b обозначают соответственно внутренний и наружный радиусы шара (рис. 21), а р _a и р _b — внутреннее и наруж­ное давления газов.

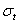
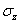
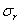
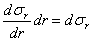
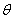
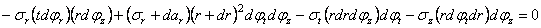
Начнем со статического обследования. Выре­жем для исследования бесконечно малый элемент двумя па­рами взаимно перпендикулярных меридиональных сечений и двумя концентрическими сферическими поверхностями. Дей­ствие отброшенных частей сосуда заменим тангенциальными ( , ) и радиальными ( ) напряжениями. Так как в рассма­триваемом случае напряжения зависят только от радиуса r , то напряжения по двум бесконечно близким друг к другу концентрическим поверхностям будут отличаться на величину и не будут зависеть от угла — другого параметра, определяющего местоположение рассматриваемого элемента. Проектируя все силы на нор­маль к элементу, имеем уравнение равновесия в виде:

.

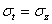
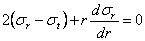
Имея в виду равенство и производя сокращения, получаем уравнение равновесия:

. (2.27)

Переходим к геометрическому обследованию. Из рассмотрения перемещений и формоизменения элемента заключаем, что относительное тангенциальное удлинение:

, (2.28)

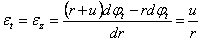
а относительное радиальное удлинение:

. (2.29)

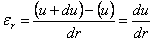
Выполним физическое обследование. Зави­симость напряжений от деформаций в данном случае имеет вид:

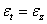
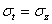
Напряжения через деформации выражаются (принимая во внимание равенство и ) так:

. (2.30)

Данные геометрического обследования используем для преобразования полученных физических зависимостей, т. е. подставляем (2.28) и (2.29) в (2.30). Имеем выражения для напряжений:

(2.31)

(2.32)

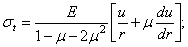
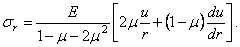
Выражения (2.31) и (3.32) подставляем в уравнение статики (12.27). Тогда после сокращений получаем выражение

, (2.33)

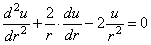
которое представляет собой уравнение, объединяющее в себе все три стороны исследования (геометрическую, физиче­скую и статическую).

Общий интеграл дифференциального уравнения (2.33) имеет вид

. (2.34)

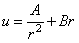
Дифференцируя (2.34), находим

. (2.35)

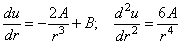
Подставляя (2.34) и (2.35) в (2.31) и (2.32), получаем вместо диф­ференциальной формы выражения для напряжений в алгебраи­ческой форме:

(2.36)

. (2.37)

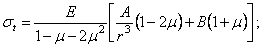
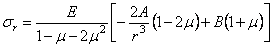
Постоянные интегрирования А и В определим из поверх­ностных условий:

.

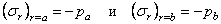
Тогда, в силу (2.37), имеем:

(2.38)

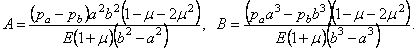
Подставляя (2.38) в (2.36) и (2.37), окончательно получим:

Для случая одного внутреннего давления р _a наибольшее растягивающее тангенциальное напряжение будет на внут­ренней поверхности сосуда (при r = a ):

а минимальное на наружной поверхности (при r = b ):

.

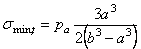
Приведенное здесь решение задачи теории упругости получено применением метода переме­щений.

2.3. Сосредоточенная сила, действующая на плоскость

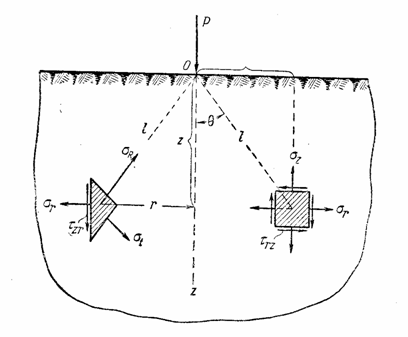
Пусть плоскость z = 0 является гранью полубесконечного сплошного тела пусть на эту плоскость действует сосредоточенная сила Р по оси z (рис. 22). В литературе эта задача име­нуется задачей Буссинеска .

Для радиального напряжения можно принять в качестве первой попытки

.

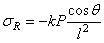
Переходя к цилиндрическим координатам, по формулам перехода должны получить

.

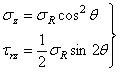
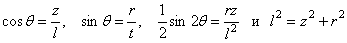
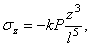
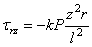
Заменяя , имеем:

(2.39)

. (2.40)

Для определения коэф­фициента k составим уравнение равновесия по какому-либо горизонтальному сечению z = a . Для элементарной площадки в виде бесконечно тонкого кольца шириной dr и радиуса r имеем элементарную внут­реннюю силу

.

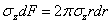
Со всех таких элементарных площадок, т. е. со всего сечения z = a , имеем сумму внутренних усилий

. (2.41)

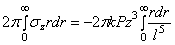
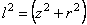
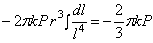
Так как , то, дифференцируя, имеем 2 ldl = 2 rdr . Таким образом, (2.41) перепишется:

.

Уравнение равновесия по сечению z = а (сумма проекций на ось z ) приводит к выражению

,

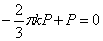
откуда .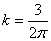

То, что выражения (2.39) и (2.40) дают точное решение задачи, можно доказать путем использования функции на­пряжений. Выполнение этой операции позволит определить нам также и другие компоненты напряжений ( , ).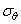

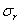
На основании (2.13, 2.14, 2.15)

.

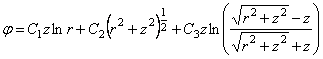
Окончательно формулы для напряжений примут вид:

. (2.42)

Для определения перемещений используем уравнения (2.2). Компо­нента смещения вдоль радиуса r

. (2.43)

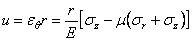
После подстановки в (2.43) выражений (2.42) и преобразо­ваний получаем

.

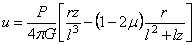
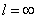
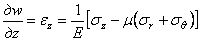
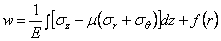
При , как и следует ожидать, и == 0. На основании этого

,

. (2.44)

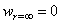
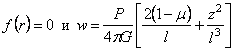
После подстановки в (2.44) выражений (2.42) и интегриро­вания, принимая также, что , получаем:

.

Для вертикальных перемещений точек на граничной плоскости z = 0 для так называемой “дневной поверхности” получим выражение:

. (2.45)

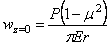
У начала координат, как это было и в плоской задаче, перемещения и напряжения становятся бесконечно боль­шими, и потому, необхо­димо представить, что у начала координат в области пла­стических деформаций материал вырезан полусферической поверхностью малого радиуса, а сосредоточенная сила Р заменена статически эквивалентными усилиями, распределен­ными по этой поверхности.

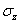
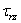
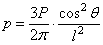
Полное напряжение в любой точке горизонтальной площадки (т.е. равнодействующая напряжений и на рис. 23)

.

Если, далее, очертить произволь­ным диаметром d сферу, касающуюся граничной плоскости в той же точ­ке O, то по всем горизонтальным площадкам, размещенным на поверх­ности этой сферы, полные напря­жения

.

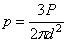
2.4 Частные случаи загрузки упругого полупространства

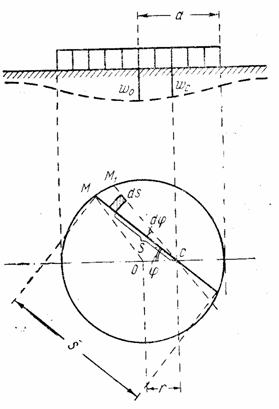
а) Равномерная загрузка по площади круга. Имея реше­ние для сосредоточенной силы, действующей на плоскую грань упругого полупростран­ства, найдем перемещения и напряжения, возникающие под действием распределенной нагрузки, если применим прин­цип сложения действия сил. Пусть нагрузка общим ве­сом Р равномерно распреде­лена на «дневной» поверхности полубесконечного тела по площади круга радиуса а . Ин­тенсивность нагрузки

.

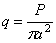
Составим выражения для перемещения точки С , нахо­дящейся на «дневной» поверх­ности, но в пределах загру­женного круга (рис. 24).

Проведем через точку С секущую МС, а в бесконечной близости другую – М₁С и рассмотрим влияние на «прогиб» точки С нагрузки, расположенной на элементарной площадке, заштрихованной на рис. 24. Эта площадка равна dF = sd 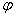ds , а нагрузка, на нее приходящаяся,

dP = qdF = qsd 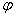ds . (2.46)

От такой нагрузки точка С должна опуститься согласно (2.45) на

и тогда получим

.

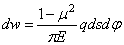
Полное перемещение точки С от всей нагрузки

.

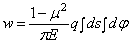
Из рис . 24 ясно, что взятый по всей длине секущей интеграл

. (2.47)

.

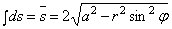
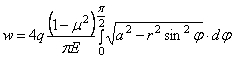
Для “прогиба” в центре круга, т. е. при r = 0, имеем:

.

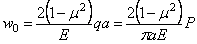
Таким образом, зная а , избавимся от бесконечности, полу­чаемой по формуле (2.45).

Для “прогиба” точек, лежащих на контуре загруженного круга, т. е. при r = а, получим:

.

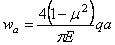
Отношение перемещений двух характерных точек

Перемещение точек, лежащих внутри загруженного круга, но не в центре его, могут быть вычислены на основании (2.48) с помощью таблиц аллиптических интегралов.

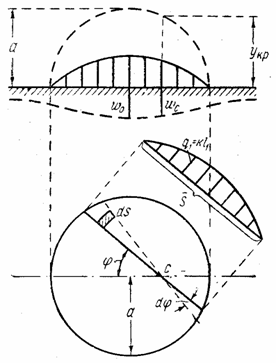
б) Загрузка на площади круга по “ полушару ”. Рас­смотрим случай, когда на площади круга радиуса а расположена нагрузка в ви­де шапки (рис. 25) таким образом, что в любой точ­ке загруженной территории интенсивность нагрузки

пропорциональна ординате полусферы, имеющей ра­диус а и основанием кото­рой служит упомянутая площадь круга. Иначе говоря, интенсив­ность нагрузки в любой точке согласно обозначе­ниям рис. 24 записывает­ся так:

;

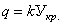
здесь У_{кр .} — ордината круга, имеющего радиус a , k — коэффициент нагрузки, т. е.

,

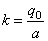
a q ₀ — наибольшая интенсивность нагрузки (т. е. в центре загруженной территории), причем q₀ может быть выражена через об­щий вес:

.

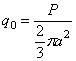
Для вычисления перемещения точки С , поступая анало­гично предыдущему примеру, имеем:

.

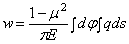
Выясним геометрический смысл последнего интеграла. Из рассмотрения рис. 25 следует, что

,

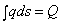
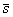
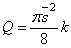
где Q — площадь эпюры нагрузки на длине . Но так как, рассекая сферу любой плоскостью, мы всегда в разрезе бу­дем получать круг, то и в данном случае, рассекая нагрузку, в общем изображаемую “ полушаром ”, мы всегда в разрезе должны получить “полукруг” (этой фи­гурой в разрезе будет полуэллипс ). Таким образом, можем записать

,

где k — коэффициент, позволяющий перейти от геометриче­ского полукруга к “полукругу” в кавычках. Итак,

или, на основании (2.47),

.

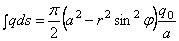
Теперь для полного перемещения точки С имеем:

.

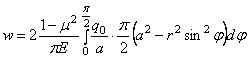
После интегрирования получаем:

, (2.49)

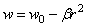
Если радиус изогнутой поверхности граничной плоскости будет велик по сравнению с радиусом загруженного круга, то выражение (2.49) можно практически считать уравнением некоторой сферической по­верхности.

в) Обратная задача. Очевидно, можно решать и обратные задачи, когда задано уравнение изогнутой «дневной» поверх­ности и требуется найти уравнение нагрузки, вызвавшей такую деформацию.

Возьмем, например, абсолютно жесткий штамп в виде круглого цилиндра, вдавливаемого в плоскую грань упругого полупространства. В этом случае перемещение w для всех точек будет по­стоянным по круглой подошве штампа; распределение дав­лений не будет постоянным и должно определяться в ре­зультате решения интегрального уравнения

Решение такого уравнения приводит к результату:

,

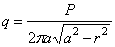
где Р — полная нагрузка на штамп, а — радиус штампа и r — радиус круга, на который действует давление q . Это рас­пределение неравномерно и наименьшее его значение в центре ( r = 0), где

,

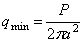
т.е. наименьшее давление равно половине среднего давле­ния по круговой площади подошвы штампа. На контуре этой площади ( r = a ) давление становится бесконечно большим.

Перемещение штампа выразится формулой

.

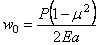
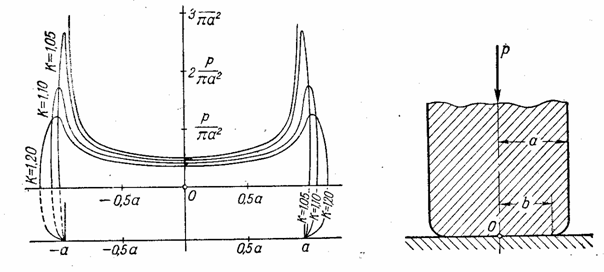
Если предположить, что края штам­па имеют некоторое закругление, как это показано на рис.26, то распределение напряжений у краев штампов может существенно измениться. Такая сложная контактная задача была поставлена И. Я. Штаерманом и при­вела к ответу, представленному графиком на рис. 26.

В частности, это решение свободно от бесконечно больших напряжений, не имеющих реального значения. На указанном графике .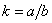

2.5 Вдавливание абсолютно жесткого шара в упругое полупространство

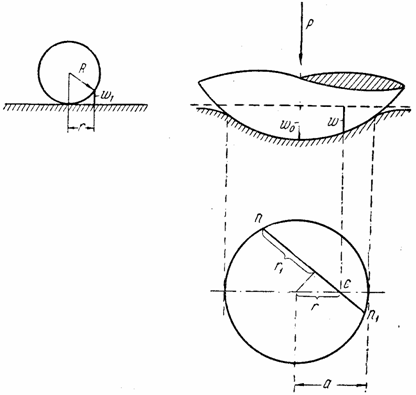
Представим, что на упругом полуространстве по­коится жесткий шар радиуса R (рис. 27). Если нет давле­ния на этот шар и исключить влияние собственного веса, то касание шара с граничной плоскостью полупространства бу­дет в точке. На расстоянии от точки касания, малом по сравнению с R , зазор между шаром и граничной плоскостью может быть, как известно, с достаточным приближением определен формулой:

.

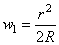
Если к шару будет приложена нагрузка, нормальная к первоначальной граничной плоскости и проходящая через дентр шара, то вследствие упругости полупространства гра­ничная плоскость изогнется и шар опустится, как это пока­зано на рис. 26 (справа).

Ввиду симметрии деформации относительно оси, совпа­дающей с направлением силы, площадка контакта шара с де­формированной граничной поверхностью упругого полупро­странства будет представлять в плане круг неко­торого радиуса а; закон распределения давления под шаром не известен, (подлежит определению). Очевидно, эпюра этого давления должна представлять фигуру, симметричную относительно оси, совпадающей с силой.

Проведя через точку С в плане бесконечно близкие секущие, вычислим нагрузку, приходящуюся на бес­конечно малую площадку dp , отстоящую на расстоянии s от точки С. Если напряжение смятия у этой площадки обозна­чим через q , то элементарная сила на площадке dF соответствует (2.45). Влияние этой силы на опускание точки Е определится, согласно (2.45), таким образом:

или, после подстановки (2.46),

.

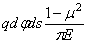
Влияние на прогиб рассматриваемой точки С всех элемен­тарных давлений со всей площади контакта шара и упругого полупространства оценится интегралом:

, (2.50)

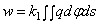
В выражении (2.50) неизвестными являются w и функция рас­пределения давления q . С другой стороны, из чисто геоме­трических соображений, поскольку шар не деформируется, следует (рис. 27) что

, (2.51)

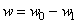
где w ₀ — опускание шара (и одновременно “прогиб” полу­пространства) в центре касания, a w ₁ — первоначальный зазор между шаром и граничной плоскостью. Тогда исследуемый прогиб

, (2.52)

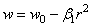
где введено обозначение:

.

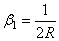
Уравнение (2.51) выражает условие, что «упругая» поверх­ность полупространства представляет под шаром часть по­верхности этого шара. Объединяя (2.50) и (2.52), имеем:

. (2.53)

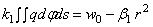
В выражении (2.53) неизвестная функция q входит под знак интеграла и, следовательно, (2.53) является интеграль­ным уравнением. Но именно такое же уравнение имелось и выше, где, наоборот, была известна нагруз­ка (он а была задана по “ полушару ”), а определялся характер изгиба граничной плоскости.

На основании сходства правых частей (2.53) и (2.49) заключаем, что эпюра распределения давления по площади контакта представляет “ полушар ”. Таким образом, если дав­ление в центре контакта обозначим через q ₀, то на расстоя­нии r от этого центра давление

,

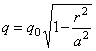
а при r = а (на контуре круга касания) обращается в нуль.

Все выражения предыдущего раздела целиком относятся и к данной задаче, т. е.

(2.54)

. (2.55)

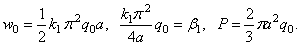
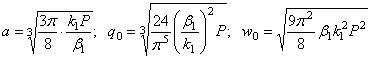
2.6. Задача об упругом смятии шаров

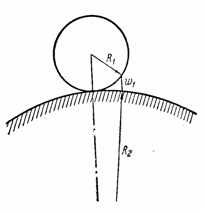
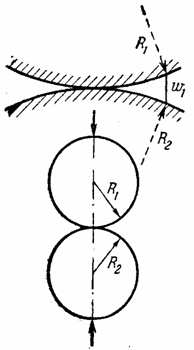
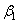
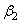
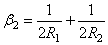
Представим, что абсолютно жесткий шар радиуса R ₁ по­коится на упругом теле сферической формы, имеющей очень большой радиус R ₂, и в дальнейшем подвергается действию силы Р (рис. 28). При вычислении глубины вдавливания радиуса площадки контакта и наибольшего напряжения смя­тия под указанным шаром мож­но использовать формулы (2.55), введя вместо прежнего новое значение , определяемое выражением:

.

Последнее выте­кает из зависимости, состав­ляемой для выбираемого перво­начального зазора w ₁ в случае касания двух сферических тел (рис. 28), и в данном случае имеем:

.

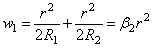
Таким образом, при вдавливании жесткого шара в “почти бесконечную” сферу, получаем

; (2.56)

; (2.57)

. (2.58)

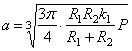
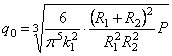
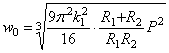
Полученные формулы могут употребляться лишь в случае, если радиус площадки смя­тия а будет весьма малым по сравнению с радиусом сферы R ₂, вследствие чего последнюю можно при небольших раз­мерах вдавливаемого шара считать “ полубесконечным ” те­лом, закон деформации которого был положен в основание вывода формул (2.55).

Если теперь представить случай двух упругих “почти бес­конечных” сфер, взаимно вдавливаемых силами Р (рис. 29), т. е. верхнюю сферу считать не абсолютно жесткой, а спо­собной деформироваться, то в этом случае можно

восполь­зоваться выводами предыдущей задачи, если ввести изменение в коэффициент, завися­щий от упругих свойств материалов, т. е. вместо k ₁ подставить

,

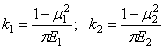
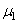
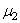
Е ₁ и — упругие характеристики матери­ала верхней сферы; E ₂ и то же для ниж­ней сферы.

Возможность такого простого перехо­да от формул (2.56), (2.57), (2.58) вытекает из тех соображений, что в данной задаче ввиду деформаций обеих сфер исходное уравнение деформации (2.53) должно быть записано в виде:

.

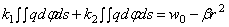
Последнее после введения обозначения (2.59), приводится к виду (2.53) с заменой k ₁ и k ₂.

Так как при сжатии упругих шаров радиус площадки смя­тия оказывается очень малым по сравнению с радиусами са­мих шаров, то рассмотренная сейчас задача о сжатии двух “почти бесконечных” сфер может быть практически исполь­зована и в задаче об упругом сжатии шаров (задача Герца). Итак, при сжатии шаров имеем:

; (2.60)

; (2.61)

. (2.62)

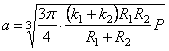
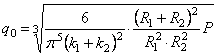
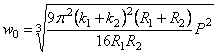
Зная закон распределения давления по поверхности контак­та, можно перейти к вычислению напряжений внутри шаров, используя для этой цели (2.42) и применяя принцип наложения.

Большой практический интерес представляет нахождение внутри сжимаемых шаров точек, имеющих большие касатель­ные напряжения. Исследование этого вопроса приводит к выводу, что точка, где касательное напряжение является наибольшим, лежит на оси z на глубине, равной примерно половине ра­диуса поверхности касания. Такую точку и следует рассматривать как самую опасную (в свете третьей теории прочности) для таких пластичных материалов, как сталь. Наибольшее касательное напряжение в этой точке (при 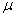= 0,3) составляет примерно 0,31 q ₀.

Из (2.60), (2.61), (2.62) следует, что радиус площадки смятия, взаимное вдавливание и напряжения смятия не находятся в линейной зависимости от силы Р. При увеличении силы Р напряжения и деформации шаров возрастают медленнее, чем возрастает сила.

Таким образом, в контактной задаче принятие в основу исследования линейной связи между компонентами напряже­ний и компонентами деформации в каждой точке упругого тела (обобщенный закон Гука) повлекло за собой нели­нейную зависимость между силой и перемещениями.

Адрес: Россия, 450071, г.Уфа, почтовый ящик 21