Уравнение спирали в полярных координатах

Уравнения кривых. Спираль Архимеда.

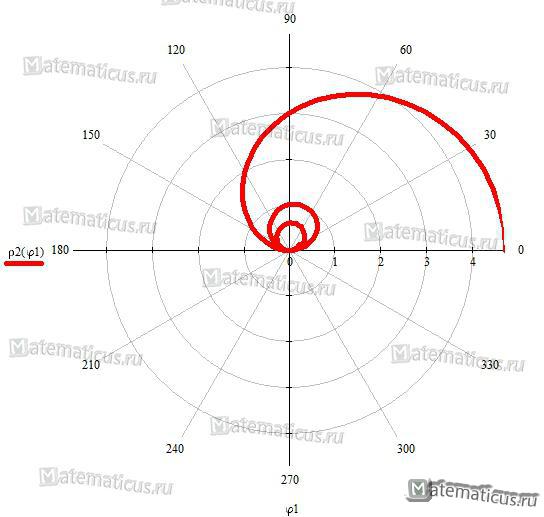
Архимедова спираль — плоская кривая сформированная траекторией произвольной точки, которая размеренно двигается по лучу берущему свое начало в O, одновременно с этим сам луч размерено обращается вокруг O. Перефразировав получаем, расстояние ρ пропорционально углу оборота φ луча. Обороту луча на одинаковый угол соответствует одно и то же увеличение ρ.

Уравнение, характеризующее Архимедову спираль, в полярной системе координат:

где k — сдвиг точки M по лучу r, при обороте на угол, который равен одному радиану.

Обороту прямой на 2π соответствует смещение a = 2kπ.

Число a — шаг спирали.

На основании этого уравнение Архимедовой спирали можно представить таким образом:

Когда поворачиваем луч против движения часовой стрелки, получаем правую спираль, когда поворачиваем — по часовой стрелке — левую спираль. При положительной величине φ формируется правая спираль, отрицательной — левая спираль.

Замечательные кривые

Семейство роз Гранди

Уравнение имеет вид:

a — радиус лепестка;

k — положительный параметр, отвечает за количество лепестков.

Рисунок 1 — роза с тремя лепестками ρ=sin3φ

Рисунок 2 — роза с 16 лепестками ρ=sin8φ

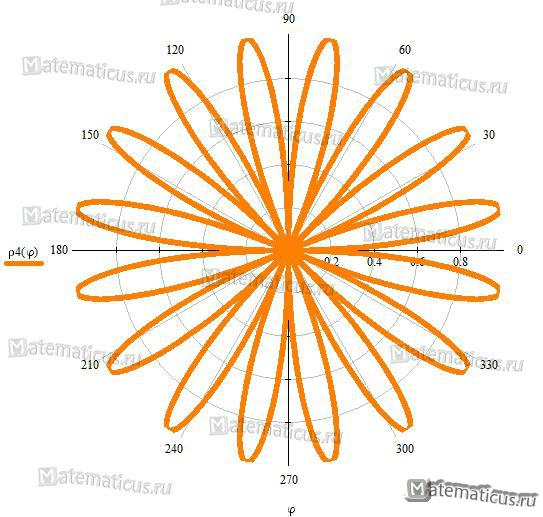
Рисунок 3 — семейство роз Гранди — напоминает ромашку ρ=sin20φ

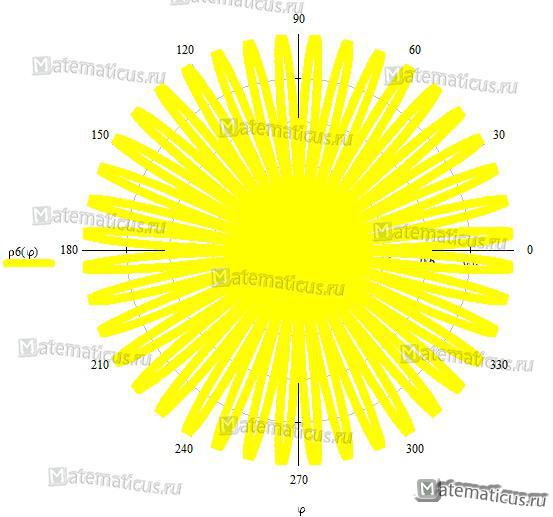
Рисунок 4 — семейство роз Гранди — линия похожа на зрачок глаза ρ=sin100φ

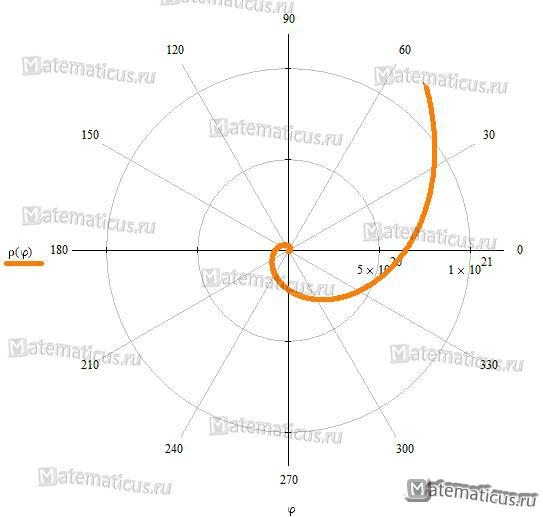
Логарифмическая спираль

Уравнение логарифмическая спираль (трансцендентная кривая) в полярных координатах:

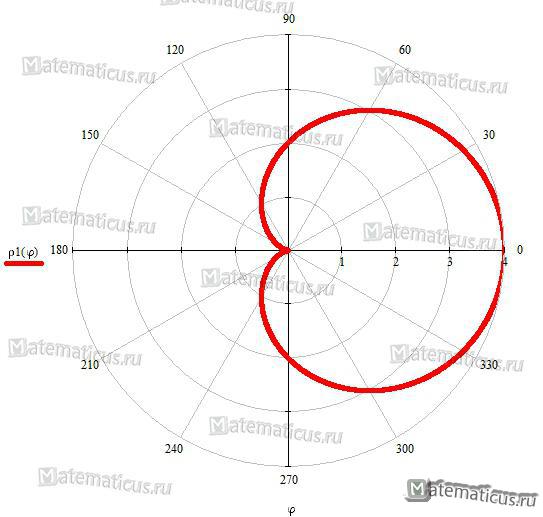
Кардиоида

Уравнение кардиоиды (перев. греч. сердце и вид) в полярных координатах:

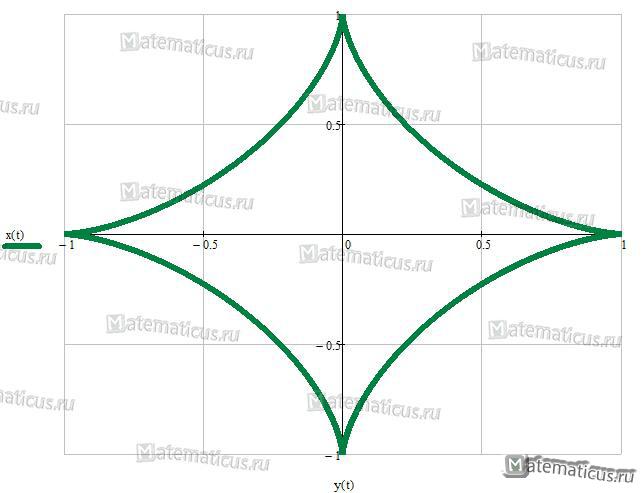
Астроида

Уравнение астроиды (перев. греч. звезда и вид) :

x 2/3 + y 2/3 = a 2/3

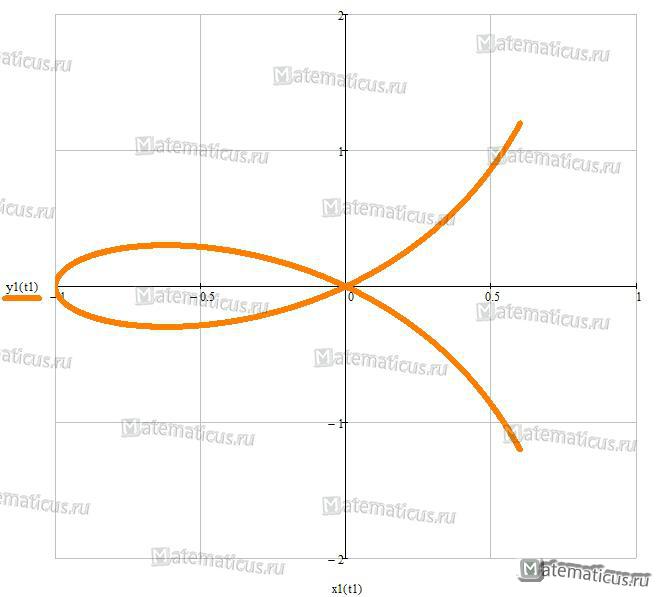
Строфоида

Уравнение строфоиды (перев. греч. крученая лента, поворот) :

y 2 (a — x)= x 2 (a + x)

Уравнение строфоиды в полярной системе координат:

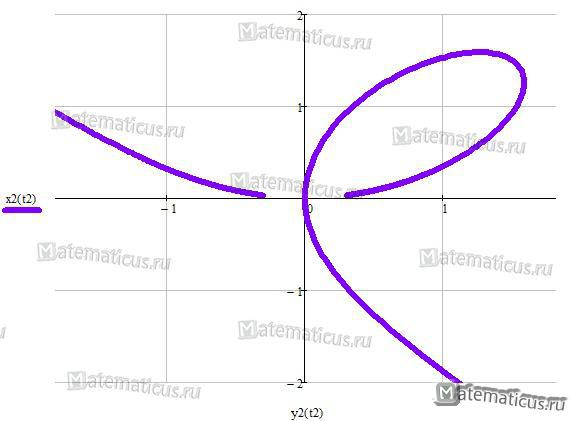
Декартов лист

Уравнение декартова листа :

x 2 + y 2 — 3axy = 0

Уравнение декартова листа в полярной системе координат:

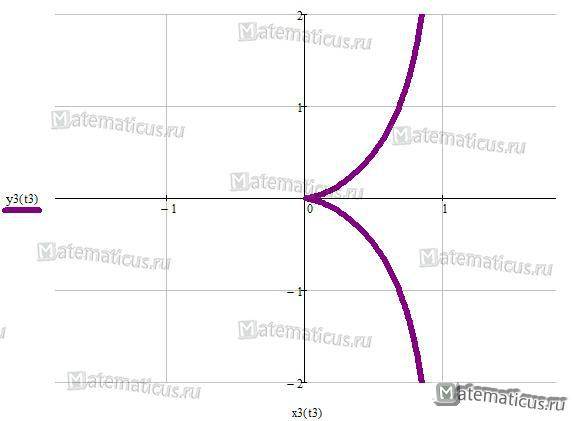
Циссоида

Уравнение циссоиды Диоклеса (перев. греч. плющ, вид) в прямоугольной системе координат :

Параметрическое уравнение циссоиды:

x = a t 2 /(1 + t 2 )

x = a t 3 /(1 + t 2 )

Уравнение циссоиды в полярной системе координат:

Циклоида

Параметрическое уравнение циклоиды :

Кохлеоида

Уравнение кохлеоиды (трансцендентная кривая) в полярных координатах:

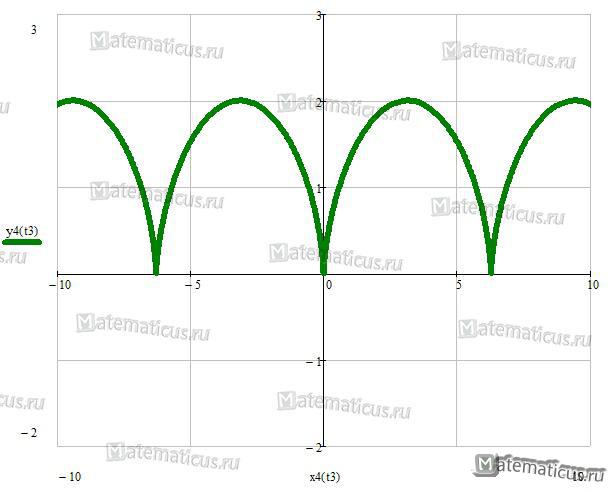
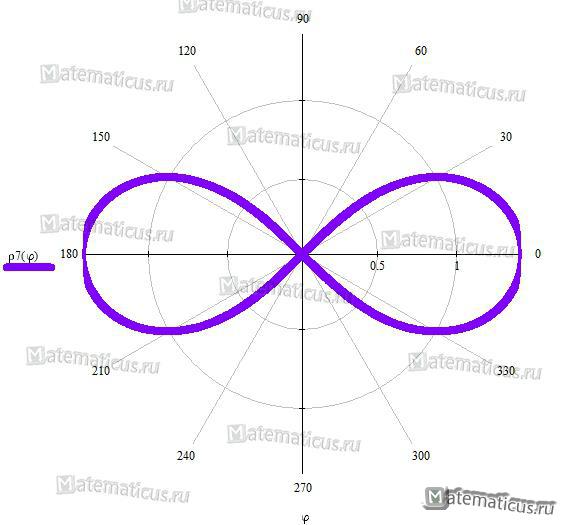
Лемниската Бернулли

Уравнение лемниската Бернулли в прямоугольных координатах:

(x 2 + y 2 ) 2 = a 2 (x 2 — y 2 )

Уравнение лемниската Бернулли в полярных координатах:

Архимедова спираль рассмотрена здесь подробно.

Применяя математические уравнения замечательных кривых, можно получить вот такие геометрические линии.

Математика, которая мне нравится

Математика для школьников и студентов, обучение и образование

Архимедова спираль

История спирали Архимеда

Архимедова спираль была открыта (правильно, Вы угадали!) Архимедом. Это произошло в III веке до н.э., когда он экспериментировал с компасом. Он тянул стрелку компаса с постоянной скоростью, вращая сам компас по часовой стрелке. Получившаяся кривая была спиралью, которая сдвигались на ту же величину, на которую поворачивался компас, и между витками спирали сохранялось одно и то же расстояние.

Использование архимедовой спирали в древности

Архимедову спираль использовали как наилучший способ определения площади круга. С ее помощью был улучшен древний греческий метод нахождения площади круга через измерение длины окружности. Спираль дала возможность более точного измерения длины окружности, а следовательно, и площади круга. Однако вскоре, когда Архимед попытался вычислить более точно значение , которое упрощало нахождение площади круга, было доказано, что спираль для этого не подходит.

Что такое обобщенная Архимедова спираль?

Обобщенная Архимедова спираль определяется как кривая, которая задается в полярных координатах уравнением (далее положим ). Спираль Архимеда, в частности, принадлежит множеству обобщенных Архимедовых спиралей.