Уравнение среднего перпендикуляра к отрезку

Please wait.

We are checking your browser. mathvox.ru

Why do I have to complete a CAPTCHA?

Completing the CAPTCHA proves you are a human and gives you temporary access to the web property.

What can I do to prevent this in the future?

If you are on a personal connection, like at home, you can run an anti-virus scan on your device to make sure it is not infected with malware.

If you are at an office or shared network, you can ask the network administrator to run a scan across the network looking for misconfigured or infected devices.

Another way to prevent getting this page in the future is to use Privacy Pass. You may need to download version 2.0 now from the Chrome Web Store.

Cloudflare Ray ID: 6dea5b1789047b33 • Your IP : 85.95.188.35 • Performance & security by Cloudflare

Серединный перпендикуляр

Что такое серединный перпендикуляр к отрезку? Что можно сказать о пересечении серединных перпендикуляров к сторонам треугольника? К сторонам многоугольника?

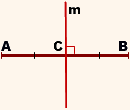
Серединный перпендикуляр к отрезку — это прямая, перпендикулярная данному отрезку и проходящая через его середину.

m — серединный перпендикуляр к отрезку AB, если

точка C — середина отрезка AB,

Чтобы построить серединный перпендикуляр к данному отрезку с помощью угольника, нужно:

1) найти середину отрезка;

2) провести через эту точку прямую, перпендикулярную данному отрезку (для этого угольник прикладываем прямым углом к середине отрезка так, чтобы она сторона угольника проходила через отрезок, а через другую сторону проводим прямую):

Свойства серединного перпендикуляра.

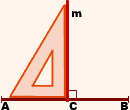
1) Геометрическое место точек, равноудаленных от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки.

Например, прямая m — геометрическое место точек, равноудаленных от точек A и B (рисунок 1).

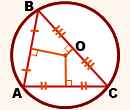
2) Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Эта точка является центром описанной около треугольника окружности.

3) Если около многоугольника можно описать окружность, то центр этой описанной окружности является точкой пересечения серединных перпендикуляров к сторонам многоугольника.

Серединный перпендикуляр к отрезку

Определение 1. Серединным перпендикуляром к отрезку называется прямая, которая проходит через середину отрезка и перпендикулярная к нему.

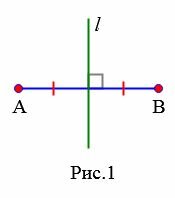На рисунке 1 прямая \( \small l \) серединный перпендикуляр к отрезку \( \small AB .\)

Теорема о серединном перпендикуляре к отрезку

Теорема 1. 1) Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. 2) Обратно: Каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.

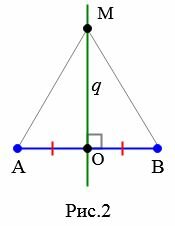Доказательство. 1) Пусть точка \( \small O \) середина отрезка \( \small AB \) и пусть прямая \( \small q \) серединный перпендикуляр к отрезку \( \small AB \) (Рис.2). Рассмотрим любую точку \( \small M \) на прямой \( \small q \). Докажем, что \( \small AM=BM. \) Если точка \( \small M \) совпадает с точкой \( \small O \), то равенство \( \small AM=BM \) верно поскольку \( \small AO=BO \) (\( \small O \)-середина отрезка). Пусть \( \small M \) и \( \small O \) различные точки. Тогда прямоугольные треугольники \( \small MOA \) и \( \small MOB \) равны по двум катетам (\( \small AO=OB \), \( \small OM \)− общий). Следовательно \( \small AM=BM. \)

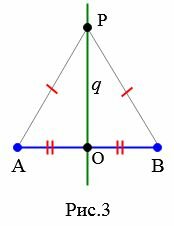2) Пусть точка \( \small P \) равноудалена от от концов отрезка \( \small AB \) (Рис.3). Тогда выполено равенство \( \small AP=BP \). Докажем, что \( \small P \) лежит на серединном перпендикуляре \( q \). Если точка \( \small P \) принадлежит прямой \( \small AB \), то поскольку она равноудалена от концов отрезка \( \small AB, \) она совпадает с точкой \( \small O \), т.е. лежит на прямой \( q.\) Если же \( \small P \) не лежит на прямой \( \small AB \), то треугольник \( \small ABP \) равнобедренный, поскольку \( \small AP=BP .\) Отрезок \( \small PO \) медиана этого равнобедренного треугольника и, значит, является также высотой этого треугольника. Тогда \( \small PO⊥AB .\) Прямые \( \small PO \) и \( q \) проходят через точку \( \small O \) и перпендикулярны к \( \small AB .\) Следовательно эти прямые совпадают, т.е. точка \( \small P \) принадлежит прямой \( q. \)