Уравнение статической характеристики замкнутой системы

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

1. Нелинейностью статической характеристики.
2. Нелинейностью динамических членов в уравнениях динамики.
3. Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

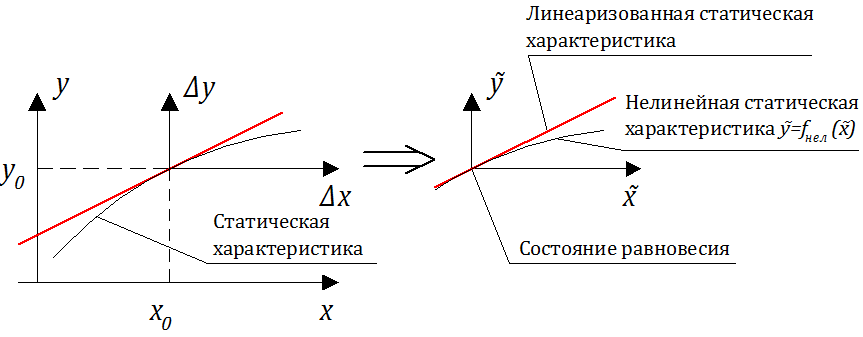
Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

1. Перейдем к безразмерным переменным (нормализованным);
2. Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_<част.>(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

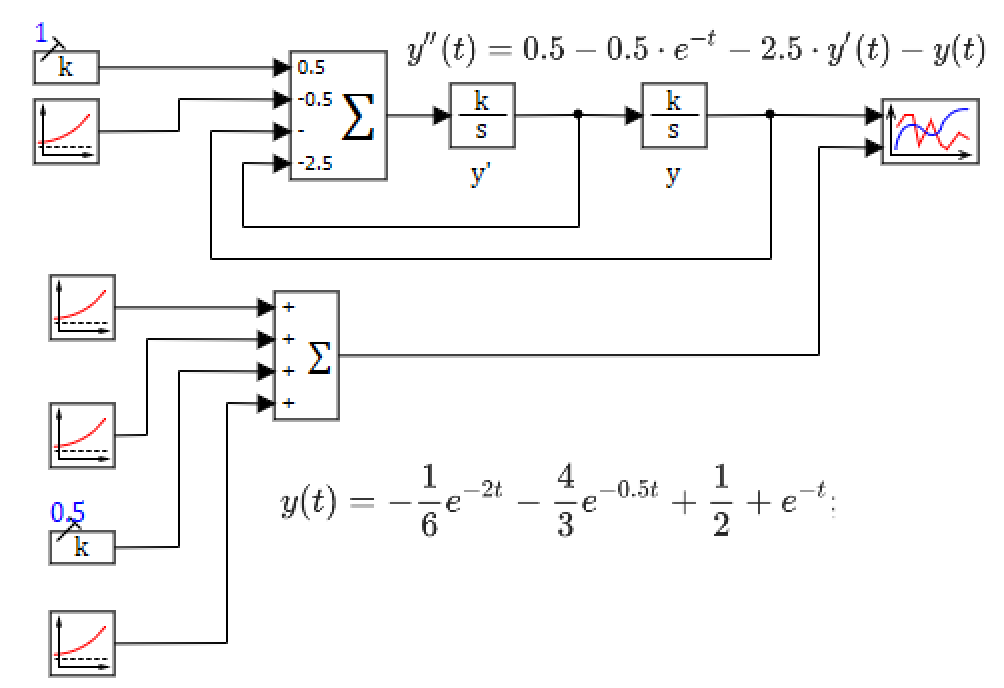
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

3.4. СТАТИЧЕСКИЕ И ДИНАМИЧЕСКИЕ ХАРАКТЕРИСТИКИ ЗАМКНУТЫХ СИСТЕМ ПРЕОБРАЗОВАТЕЛЬ – ДВИГАТЕЛЬ

Прежде чем перейти к анализу и синтезу конкретных систем управления электроприводами остановимся на основных понятиях и параметрах, характеризующих качественные и количественные показатели этих систем.

Замкнутые системы управления электроприводами (СУЭП), как и любые электротехнические устройства, в первую очередь, должны удовлетворять общим технико-экономическим требованиям (надежность, технологичность конструкции, удобство эксплуатации, минимальная стоимость, заданные габариты, масса и др.). Кроме того, к таким системам предъявляется и целый ряд требований, обусловленных в каждом конкретном случае специфи­кой технологического процесса и режимом работы производственной машины. Среди них важнейшее место занимают требования обеспечения заданных статических и динамических характеристик электро­привода. Эти требования в значительной мере определяют выбор струк­туры СУЭП и ее параметров, что составляет одну из главных задач проектирования автоматизированных электроприводов. Замкнутые СУЭП, функционирующие как автоматические системы регулирования, выполняют с питанием двигателя от управляемого преобразователя. Поэтому их часто называют замкнутыми системами преобразователь – двигатель (П — Д) или, иначе, системами П — Д с обратными связями.

Статическая характеристика замкнутой системы П—Д представляет собой графическое изображение зависимости регулируемой переменной системы от основного возмущающего воздействия f₁ двигателя в устано­вившемся режиме при фиксированном значении задающего воздей­ствия g и отсутствии других возмущающих воздействий f₂, f₃, … . Влияние последних сказывается в виде «дрейфа» статической характе­ристики или приводит к искажению ее формы. Статическая характе­ристика может иметь несколько участков разной формы, каждый из которых соответствует определенным структурам или параметрам системы, если они фиксировано изменяются в процессе управления. На рис. 3.6 показана статическая механическая характеристика Ш, типичная для многих замкнутых систем П—Д. Она представляет собой зависимость скорости двигателя ω от развиваемого им момента М при использовании различных регулирующих обратных связей.

На этом же рисунке изображено семейство Р статических механических характеристик разомкнутой системы П – Д. Каждая из этих характеристик отвечает фиксированному значению X_i управляющего сигнала х. Характеристика З состоит из двух участков. На участке 1 действуют обратные связи, стабилизирующие скорость двигателя. Поэтому здесь регулируемая величина у’ = ω’, а момент двигателя можно рассматривать как основное возмущающее воздействие, поскольку в установившемся режиме М’ = М’_с. Когда М’ = 0, скорость имеет значение Y’_о = ω_о‘, а управляющий сигнал х’ — Х’_о. При увели­чении момента нагрузки под влиянием обратных связей происходит непрерывный переход с одной механической характеристики разомкну­той системы на другую вследствие возрастания управляющего сигнала (характеристики Р при Х’₁, Х’₂ Х’₃, …). Поэтому характеристика З, представляющая собой совокупность точек семейства Р, становится на участке 1 значительно жестче характеристик разомкнутой системы. Перепад скорости на этом участке Δω_з = ω_о‘ – ω₁‘ (т.е. ΔY₁ = Y_о –Y₁) при изменении момента от М’ = 0 до М’ = М₁‘ (F₁ = F_{f (1)}) характеризует стабильность регулирования, т.е. точность поддержания постоянства скорости при наличии возмущающего воздействия F₁ = М’_с.

Рис. 3.6. Статические характеристики систем П – Д

При переходе к участку 0 характеристики 3 стабилизирующие скорость обратные связи отключаются и вводится в действие отрица­тельная обратная связь по моменту, т.е. изменяется структура системы. Последняя теперь будет работать в режиме автоматического регулиро­вания момента двигателя, т.е. здесь у» — М». При этом скорость двигателя представляет собой основное возмущающее воздействие. При неподвижном двигателе y ′′ = М_о ′′ и управляющий сигнал х» = X_J. С увеличением скорости, благодаря действию регулирующей обратной связи по момен­ту, растет сигнал х», принимая последовательные значения Х’₁, X′₂, X′₃, … , что отвечает переходу изображающей точки характеристики З по соответствующим характеристикам семейства Р. Поэтому на участке 0 замкнутой системы значительные изменения скорости сопровож­даются относительно небольшими изменениями момента. Перепад момента ΔМ ′ = М»_о — М»₁ (т.е. Δ Y_{f р} = Y_раз – Y₁) определяет здесь точность поддержания постоянства момента при изменении возмущаю­щего воздействия от ω» = 0 (ft = 0) до ω » = ω ₁ ′ (ft = F_{f (1)}). Участок 0 предусматривается, например, для ограничения момента двигателя в процессе его пуска, для защиты технологической машины от пере­грузки и т.д.

Приведенная на рис. 3.6, а характеристика З отвечает случаю, когда на обоих ее участках система регулирования, изменяя структypy, остается статической системой. Для таких систем иногда пользуются понятием статизма системы, который характеризуется вели­чиной

где G — заданное установившееся значение регулируемой величины; Y_i — установившееся значение регулируемой величины, соответствующее неизменному во времени возмущающему воздействию F_f1 (рис. 3.6, б).

Для простоты полагаем, что на вход системы по цепи обратной cвязи подается полная величина Y, где она сравнивается с G.

Статизм S может быть выражен как сумма статизма по заданию S_x, и статизма по возмущению S_f :

гдe Y₀ — значение регулируемой величины при F₁ = 0.

Вследствие статизма S_g фактическое значение регулируемой вели­чины даже при отсутствии возмущения отличается от заданного на величину G—Y₀ (рис. 3.1, б). Статизм S_f обусловливает дополнительное отклонение регулируемой величины от значения Y₀. Это отклонение при = F₁₍₁₎ имеет значение ΔY₁ = Y₀ — Y₁.

Статизм системы зависит от ее параметров, в первую очередь, от коэффициента передачи разомкнутой системы

где Хi и Y_0pi — соответственно значения управляющего сигнала и регулируемой величины при f₁ = 0 для i -й характеристики разомкнутой системы (предполагается, что величина К остается одной и той же для всех характеристик, также и перепад Δ Y_1р для них одинаков). Замкнутая система при f₁ = 0 работает на характеристике 0 разом­кнутой системы, и Y₀ = Y_0p0 (рис. 3.1, б). При этом управляющий сигнал Х₀ = G – Y₀. Учитывая (3.3), можно записать:

При f₁ = F₁₍₁₎ замкнутая система работает на характеристике 1 разомкнутой системы, для которой Y_op1 =Y₁ + ΔY_1p. При этом управ­ляющий сигнал X_l = G — Y₁. С учетом (3.3) находим

После подстановки в (3.2) значений Y₀ и Y₁ из (3.4) и (3.5) получим

Для оценки наклона участка статической характеристики удобнее пользоваться понятием статизма характеристики

В системах, астатических по возмущению f₁ значения S_f и S_x равны нулю.

Таким образом, путем выбора соответствующих обратных связей и значений коэффициента передачи системы, а в необходимых случаях, перехо
дя к использованию астатического регулирования, можно в зам­кнутых системах П—Д формировать статические характеристики прак­тически любого вида.

Динамические характеристики замкнутых систем П – Д отражают поведение этих систем в переходных процессах пуска, торможения, регулирования скорости, наброса и сброса нагрузки и т.п., т.е. при изменениях задающего или возмущающего воздействия. Эти характе­ристики представляют собой графики изменения во времени регули­руемых величин: ω = f (t), М = q (t), dω/dt = φ (t) и др.

Учебное пособие: Замкнутые системы управления

ЗАМКНУТые СУЭП

В замкнутой СУЭП (или системе с отрицательной обратной связью) управление U(t) формируется в зависимости от отклонения управляемой переменной у(t) от задающего воздействия x(t).

Точность стабилизации координаты оценивается отклонением ее от заданного значения под действием возмущающего воздействия.

Во многих промышленных механизмах системы регулирования предназначены для стабилизации с заданной точностью скорости w и момента М электродвигателя и связанного с ним рабочего механизма при действии на систему различного рода возмущений. Одним из основных возмущающих воздействий, влияние которого должно быть скомпенсировано системой является момент статического сопротивления М_с (t) на валу ЭД.

Регулирование скорости с высокими статическими и динамическими свойствами в настоящее время проектируются с помощью одно- и многоконтурных систем с различными видами обратных связей.

В одноконтурных системах применяются следующие обратные связи: отрицательная по скорости, отрицательная или положительная по току и отрицательная по напряжению;

В двухконтурных системах — сочетание перечисленных обратных связей одноконтурных систем.

По структуре замкнутые СУЭП выполняются трех видов:

— с общим сумматором;

— с независимым регулированием параметров;

— системы подчиненного регулирования.

Система с общим сумматором

В системе для регулирования параметров используется непрерывное и задержанное (с отсечками) ОС.

Все сигналы суммируются с задающим сигналом Uз на входе усилителя У, который служит для повышения коэффициента усиления системы.

Такие системы обычно используют для регулирования одного параметра (скорости).

Настройка качеств регулирования осуществляется компромиссно для разных параметров. Независимая настройка каждого параметра невозможна.

Система с независимым регулированием

Каждому параметру соответствует свой регулятор Р₁ -Р_n и свой сигнал задания ( U_з1 . U_зn ) .В такой системе в каждый момент времени регулируется только один параметр. Это обеспечивает логическое переключающее устройство ЛПУ , которое подключает на вход системы выход регулятора воздействие которого в данный момент является определяющим .

Система подчиненного регулирования

Регулирование параметров осуществляется последовательно. Каждому регулирующему параметру соответствует свой регулятор . Задающий сигнал каждого последующего регулируемого параметра соответствует выходу предыдущего регулятора.

Поэтому регулирование каждой координаты подчинено регулированию предыдущей. Эта система позволяет настраивать каждый параметр отдельно начиная с внутреннего.

КОМБИНИРОВАННАЯ СУЭП (замкнуто-разомкнутая)

Управление U(t) формируется в зависимости как от отклонения e(t), так и от внешних воздействий x(t), f(t).

Комбинированные системы различают по виду используемых внешних воздействий на системы:

— с разомкнутой цепью управления по возмущающему воздействию; (рис.4)

— с разомкнутой цепью управления по задающему воздействию. (рис. 5)

Комбинированную СУЭП с разомкнутой цепью по возмущающему воздействию; применяют при действии интенсивной помехи.

Комбинированная СУЭП с разомкнутым каналом по управляющему воздействию, применяется для улучшения отработки задания. Улучшенные точность и быстродействие есть результат совместной работы грубой разомкнутой и точной замкнутой систем управления.

Проектирование САУ ЭП с заданными показателями качества

Главное требование к САУ ЭП — обеспечение заданных статических и динамических характеристик, при которых работа ЭП удовлетворяет требования техпроцесса. Основное требование к системе управления — обеспечение допустимого значения ошибки управления e(t) = х(t)-y(t) в установившихся и переходных режимах, что определяется статическими и динамическими характеристиками САУ ЭП.

Статическая характеристика замкнутой СУЭП — зависимость регулируемой переменной от основного возмущающего воздействия f₁ при постоянном задающем воздействии X и при отсутствии других возмущающих воздействий. Статическая характеристика может иметь несколько участков разной формы, каждый из которых соответствует определенным структурам и параметрам системы (рис. 6).

I- участок стабилизации скорости, CУ с отрицательной обратной связью по скорости.

II- участок стабилизации момента, СУ с О.О.С. по моменту сопротивления.

Данная статическая характеристика имеет два участка I и II, каждому из которых соответствует определенная структура СУЭП.

Статизм системы определяет точность работы системы в установившемся режиме.

, где

— статизм, обусловленный задающим воздействием,

— статизм, обусловленный возмущающим воздействием,

X- заданное значение установившейся регулируемой величины,

Y₁ — установившееся значение регулируемой величины, соответствующее возмущающему воздействию f₁ ,

Y_о — установившееся значение регулируемой величины при f₁ =0.

Определим, как зависит величина S_x и S_f от параметра К — коэффициент передачи системы.

f₁ = 0; e_о = Х-Y_o ;

f₁ ¹ 0; e₁ = X- Y₁ ;

где

DY₁ — падение значения регулируемой переменной в замкнутой системе под действием возмущения f₁ (Рис. 9);

DY_1Р — падение регулируемой переменой в разомкнутой системе при действии f₁ ;

Y_o — значение регулируемой переменной при f₁ =0 по характеристике замкнутой системы;

Y₀₁ — значение регулируемой переменной при f₁ =0 по характеристике разомкнутой системы, проходящей через точку (Y₁ ;f₁ ) характеристики.

Следовательно: величины S_x и S_f обратно пропорциональны величине К, а S_f , кроме этого, зависит от величины задания Х, т.е. максимален на нижнем диапазоне регулирования при Х=Х_min .

Динамическая характеристика замкнутой СУЭП отражает поведение системы в переходном процессе (п/п) пуска, торможения, регулирования скорости, наброса и сброса нагрузки, т.е. при изменении задающего или возмущающего воздействия. При исследовании системы применяют воздействие в виде скачка: x(t) = X |(t) и f₁ (t) = F₁ |(t), где |(t)- единичная ступенчатая функция.

Прямые показатели качества :

Быстродействие — продолжительность п/п, т.е. длительность t_п/п до условно установившегося значения регулируемой переменной, когда ее отклонение не превышает a (3 ¸ 5% от установившегося значения) т.е.

От быстродействия зависят: динамическая ошибка в системе стабилизации при набросе нагрузки, точность в системах следящих и программного управления. Быстродействие системы ограничивается перегрузочной способностью двигателя, di/dt, допустимым ускорением механизма.

Перерегулирование — отклонение величины max превышения регулируемого параметра над установившемся значением к величине приращения ее установившейся величины. Обычно t_доп. £ 18 ¸ 30%, иногда t_доп. = 0 (привода подачи станков).

Число колебаний регулируемой величины за время t_п/п — определяет демпфирование колебаний в системе. Обычно число колебаний не более трех для избежания резонанса в ЭП.

Для систем, работающих в режиме пуска торможения, оптимальным по быстродействию будет трапецеидальный график изменения крутящего момента ЭД (при Мс = 0). Время переходного процесса будет минимально, если п/п будет происходить при :

dМ/dt = мах доп., соответствует e_доп. (рис. );

М max _доп и e_доп (допустимое ускорение) определяются перегрузочной способностью двигателя, механизма передачи, технологическими характеристиками.

Формирование требуемых переходных процессов производится за счет линейных законов изменения или формирования сложных зависимостей задания Х(t) для нескольких контуров регулирования.

Проектирование СУЭП с заданными показателями качества невозможно без анализа и исследования модели САУЭП. Моделью может быть реальное техническое устройство и абстрактное математическое описание, т.е. различают моделирование физическое и математическое. В основу физического моделирования положено изучение процессов на моделях одной физической природы с оригиналом. Математическое моделирование основано на тождественности дифференциальных уравнений, описывающих процессы в оригинале и функциональные зависимости между выходными величинами на модели. Математическое моделирование позволяет прогнозировать динамические характеристики реальной системы при свойственных ей внешних воздействиях, определить показатели качества системы и их соответствие заданию. Математическое моделирование реализуют на ЭВМ. Машинное моделирование наиболее широко применяется в форме структурного моделирования.

Математическая модель при структурном моделировании представляет собой систему дифференциальных уравнений, каждое из которых представляет элементы САУЭП: преобразователь, якорную цепь двигателя и его механическую часть, регуляторы, цепи обратных связей и другое. Составлять математическую модель удобно на основании структурной схемы для исследования динамики СУЭП. При составлении дифференциального уравнении, описывающего звено ЭП, учитываются его статические и динамические характеристики: коэффициент передачи звена, постоянные времени.

Тиристорный преобразователь в динамике представляет сложное нелинейное звено, что связано с его неполной управляемостью. Частота управления ограничена

w_о = 2pf_с ; f_с = 50 Гц; m- число фаз. (рис. 12).

СИФУ — система импульсно-фазового управления тиристорами;

СВП — собственно вентильный преобразователь.

При безинерционном СИФУ передаточная функция ТП,

W_тп =Dе(Р)/DUу(Р)=К_п е — t р — импульсное звено чистого запаздывания; где

t- среднестатическое запаздывание: t=1/Р_п f_c ;

Р_п — число пульсаций за период;

Импульсное звено чистого запаздывания аппроксимируется апериодическим звеном:

где

Если на входе СИФУ находится фильтр (апериодическое звено) для уменьшения помех с постоянной времени Т_ф , передаточная функция ТП примет вид:

Дифференциальное уравнение, описывающее зависимость между Е_п и U_у ТП:

К_п — статический коэффициент передачи ТП. В зависимости от вида опорного напряжения СИФУ К_п может быть постоянной или переменной величиной. (рис. 13).

При синусоидальном опорном напряжении статическая характеристика ТП линейная, т.е. К_п = const. При пилообразном опорном напряжении статическая характеристика нелинейна. Такой ТП моделировать сложнее. Внутренне сопротивление и индуктивность силовой цепи ТП учитываются в эквивалентных параметрах якорной цепи двигателя, питаемого от ТП.

В оптимизированных замкнутых системах Т_п принимают за некомпенсированную постоянную времени Т_m =Т_п =(3¸20) мс.

Генератор постоянного тока

ГПТ-генератор постоянного тока;

ОВГ-обмотка возбуждения генератора;

U_г -напряжение на зажимах генератора;

U_вг -напряжение ОВГ.

Передаточная функция, описывающая генератор постоянного тока:

,

где U_г — коэффициент усиления генератора:

;

U_гн -номинальное напряжение;

T_вг — постоянная времени ОВГ,

;

R_вг ,L_вг — сопротивление и индуктивность ОВГ.

В случае использования генераторов с несколькими обмотками его постоянная времени:

T_вгi — постоянная времени i-ой обмотки.

Аналогично рассматриваются параметры других звеньев СУЭП.

Cтруктурное представление ЭП постоянного тока. Передаточные функции по управляющему и возмущающему воздействию.

Считая, что ТП-безинерционный элемент , система уравнений, описывающая ЭП имеет вид:

,

.

Коэффициенты передачи по ЭДС и моменту в системе СИ одинаковы, поэтому будем их обозначать как –КФ

,.

Запишем уравнения в операторной форме

,

,

где .

Выразим из 1-го уравнения ток ,а из 2-го -скорость, разделим 1-е уравнение на и обозначим:

,,

,

.

Получим передаточные функции между напряжением и током и между моментом и скоростью.

Рассмотрим передаточную функцию всей системы по управляющему воздействию

=.

,

— коэффициент передачи ЭП по управляющему воздействию .

Рассмотрим передаточную функцию по возмущающему воздействию

Характер переходного процесса по управляющему воздействию определяется корнями характеристического уравнения

Т_м Т_э p 2 +T_м p+1=0.

— корни уравнения будут вещественными отрицательными при Т_м 1. Корень уравнения положительный. Система неустойчива-4.

Разомкнутая САУ с характеристическим полиномом 2-го порядка соответствует колебательному звену. Передаточная функция замкнутой системы также колебательное звено. Корни уравнения:

; .

;

.

Из условия для разомкнутой системы получим

,

,

с ростом kk_c увеличивается склонность к колебательному процессу.

Однако при любых kk_c замкнутая система остается устойчивой, т.к. у обоих корней вещественная часть отрицательная.

Этот метод анализа называется корневым методом.

Согласно критерию замкнутая система устойчива если

, .

Этот критерий позволяет определить факт устойчивости: главный определитель и его диагональные миноры должны быть >0.

3. В системах высоких порядков, при большой Т_ос могут возникнуть колебания. Это можно исследовать по диаграмме Вышнеградского.

Из характеристического уравнения 3-го порядка определим координаты M,N.

;

1.Найквиста — позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой. Соответственно передаточная функция разомкнутой системы заменяется p ® jwи строится АФХ на комплексной плоскости. Если АФХ не охватывает точку (-1; j0) то замкнутая система устойчива.

2.Михайлова – определяет устойчивость замкнутой системы. Система устойчива, если при увеличении w от Æ до ¥ конец вектора на комплексной плоскости опишет кривую, которая начинается на (+)-й части вещественной оси и последовательно обойдет против часовой стрелки n-квадратов, где n – порядок характеристического уравнения.

3.Метод вещественно-частотной характеристики и ЛАЧХ.

Методы графические и графо-аналитические (методы Башарина и Суворова), методы цифрового и аналового моделирования.

СИСТЕМЫ АВТОМАТИЧЕСКОГО РЕГУЛИРОВАНИЯ С

СУММИРУЮЩИМ УСИЛИТЕЛЕМ

Упрощенная принципиальная схема регулятора w ЭП постоянного тока с отрицательной обратной связью по напряжению, току и скорости на рисунке 20.

На рисунке приняты следующие обозначения:

М- ДПТ с независимым возбуждением;

ТП- тиристорный управляемый преобразователь;

УС- сумматор-инвертор на базе УПТ с коэффициентом усиления 1;

УК- корректирующее устройство на базе УПТ;

Rш- шунт датчика тока;

Rп- делитель напряжения (датчика напряжения);

ДТ, ДН, ДС- датчики тока, напряжения, скорости (усилитель, преобразователь, фильтр).

СУЭП строятся на типовых элементах УБСР: УБСР-А (аналоговые), УБСР-Д (дискретные), УБСР-АИ, УБСР-ДИ (с интегральными составляющими в регуляторах).

В состав УБСР входят источники питания, задатчики входных сигналов, датчики измерения регулируемых параметров, усилители, корректирующие устройства КУ, гальванические развязывающие устройства; устройства защиты УЗ, устройства коммутации, устройства логики УЛ и т.д. Основной элемент аналоговой серии УБСР-АИ является УПТ (операционный усилитель) на микросхемах К553УД2 и К140УД7.

К140УД7 — операционный усилитель с внутренней коррекцией АЧХ,

коэффициент усиления — К_у =(2¸3)10 4 ;

напряжение питания — U_пит ± 15В;

входное напряжение — U_вых = 10В.

УС — операционный усилитель для суммирования задающего сигнала U₃ и сигналов обратной связи: U_от , U_он , U_ос .

Если R₃ = R_c = R_н = R_т + R_ос , коэффициент усиления равен 1.

УК- операционный усилитель, может выполнять функцию:

инвертора напряжения, если Z_вх = Z_ос = R;

корректирующего устройства, структура и параметры которого определяются характером комплексных сопротивлений Z_вх и Z_oc .

В этом случае КУ может быть интегральным, дифференциальным, пропорционально- интегральным регулятором и т.п.

Датчики: для получения сигналов обратных связей.

Основные четыре вида датчиков: скорости, напряжения, тока и положения. Датчики момента, усилия, мощности получают путем соответствующей обработки сигналов датчиков тока и напряжения.

Датчики скорости : аналоговые и дискретные.

Аналоговые — тахогенераторы постоянного тока (серии ПТ) и переменного тока (серии ТТ).

Дискретные — модуляция источника света на фотоприемник.

Датчики тока и напряжения должны обеспечить гальваническую развязку сигнала обратной связи от силовой цепи. Датчики системы УБСР обеспечивают гальваническую развязку до 1000В, а датчики тока и магнитного потока, использующие эффект Холла — несколько тысяч вольт. Сигнал на ДТ снимается с шунта или трансформатора тока, на ДН- с делителя напряжения. Сигнал усиливается, выпрямляется (после демодуляции в устройстве гальванической развязки) и фильтруется (RС- фильтр).

Пример датчиков тока и напряжения производства ХЭМЗ:

ДТ- ЗАИ и ДН- 2АИ.

ДТ подключается к шунту, сигнал гальванически развязан, Uвых=±10В; Кус=35- 135 погрешность менее 1%; на выходе RС фильтр с постоянной времени t_ф = 2мс.

1) Бесконтактные сельсинные командоаппараты с ручным приводом — для ввода задания.

Тип СКАЗ- 41, U_пит = 110В, f=50Гц, U_вых снимается с роторной обмотки; угол a=±60 о .

2) Задатчик скорости — для систем автоматического регулирования скорости.

Блоки задания скорости : БЗС — на базе б/к сельсина БД- 404, связано с исполнительным двигателем РД- 09. Угол поворота задается микровыключателями.

БЕШД — б/к сельсин с приводом от шагового двигателя через редуктор.

БСР — задатчик скорости реостатного типа с приводом от РД-09 через редуктор. Интенсивность роста задающего напряжения задается заменяемым редуктором с различными коэффициентами передачи. На выходе сельсинов устанавливается фазочувствительный усилитель ФВ-1АИ с U_вых =±10В.

Регуляторы в системе неподчиненного регулирования строятся на базе ОУ, которые имеют специальные свойства:

-выход усилителя инверсный по отношению ко входу.

-ОУ может и должен работать в условиях действия глубоких ОС, вплоть до закорачивания вход/выход.

.

выходной сигнал — импульс ¥ амплитуды и Æ длительности.

Является источником высокочастотной помехи.

где К_п — коэффициент усиления пропорциональной части ПИ-регулятора;

Т_и — постоянная времени интегральной части;

.

Передаточная функция звена будет иметь вид:

.

— апериодическое звено;

_.

Реализация сложных регуляторов по их передаточным функциям.

Сложный регулятор — регулятор, который не может быть реализован на одном ОУ.

Регулятор скорости с отрицательной обратной связью по скорости

Рассмотрим статические и динамические характеристики регуляторов скорости с различными видами обратных связей. При этом понимаем, что все элементы , образующие систему , являются линейными стационарными .

Структурная схема системы регулирования скорости с обратной связью по скорости представлена на рис.10-3

На структурной схеме (Рис.10-3.) приняты следующие обозначения:

R(Р)- передаточная функция регулятора;

— датчик скорости;

Т_с — постоянная времени фильтра;

K_c — коэффициент передачи обратной связи по скорости;

K_п , Т_п — коэффициент усиления и постоянная времени тиристорного преобразователя;

Т_э , Т_м — электромагнитная и электромеханическая постоянная времени двигателя;

;

R_э и L_э — эквивалентные сопротивления и индуктивность якорной цепи;

1/К_д =C- внутренняя отрицательная обратная связь по ЭДС двигателя,

C- постоянная двигателя при Ф=const. C=кф;

J-момент инерции двигателя с рабочей машиной.

Статический регулятор скорости

Регулятор пропорционального типа с коэффициентом передачи К_р .

Определение статических характеристик:

w=f(U₃ ); w=f(I_cт ), т.е. зависимости скорости от задающего и возмущающего воздействия.

Преобразуем структурную схему: вынесем возмущение I_ст из замкнутого контура, затем преобразуем замкнутый контур двигателя в динамическое звено без обратной связи (Рис. 10-4.).

Положив в полученной схеме р=0,что соответствует установившемуся режиму получим :

где К=К_р ×К_п ×К_с ×К_д — коэффициент усиления разомкнутой системы;

В разомкнутой системе :

На рис. представлены статические характеристики

а) при I_С =0;

в) при.

Т.к. в прямой цепи замкнутого контура системы нет идеального интегрирующего звена, рассматриваемая система является статической как по возмущающему (I_с ), так и по управляющему (U₃ ) воздействиям и имеет статические ошибки по этим воздействиям.

Определим статическую ошибку по возмущающему воздействию I_с . т.е. выражение для Dw_I совпадает с величиной падения скорости в замкнутой системе.

Рисунок 10-6- статическая характеристика Dw_I = f(Ic).

Характеристика построена для w₀₃ =const для различных коэффициентов усиления К2>К1>0.

Статическая ошибка по возмущающему воздействию прямо пропорциональна величине нагрузки, характеризуемой Iс, и обратно пропорциональна коэффициенту усиления К.

Статическая ошибка по управляющему воздействию U₃

U_eо — статическая ошибка по управляющему воздействию замкнутой системы при I_с = 0,

DU_{e I} — приращение статической ошибки, обусловленное I_с .

DU_e увеличивается с возрастанием нагрузки I_с Рис. 10-7.

для оценки влияния отрицательной обратной связи по скорости, типа и параметров регулятора на свойства регулятора скорости сравним передаточные функции (п.ф.) разомкнутых и замкнутых систем регулирования W.

Примем Т_с и Т_п равными 0 ввиду их малости по сравнению с Т_э и Т_м . Передаточная функция системы по управляющему воздействию:

.

Линейная стационарная система второго порядка всегда устойчива. Предельный коэффициент усиления К_пр = ¥. Качество переходного процесса полностью определяется относительным коэффициентом демпфирования x и собственной частотой колебания W_о (при x = 0).

Собственная частота W_о характеризует быстродействие системы; чем больше W_о , тем быстрее затухает переходной процесс.

Для разомкнутой системы :

При x 1- переходной процесс апериодический.

При x=0- незатухающие гармонические колебания.

Передаточная функция замкнутой системы по управляющему воздействию

Для замкнутой системы:

То есть, жесткая отрицательная обратная связь по скорости увеличивает W_о и уменьшает x₃ в раз. Значит с ростом К возрастает скорость затухания и уменьшается колебательность (перерегулирование) переходного процесса. Жесткая отрицательная обратная связь по w улучшает устойчивость, т.к. уменьшается Т_м и Т_э Т_м в (1+К) раз. Аналогично исследуются переходные процессы, обусловленные действием нагрузки в виде ударного приложения Мс (или I_с = К_д М_с ) к валу двигателя.

Переходная функция замкнутой системы по возмущающему воздействию:

где I_д , M_д — динамические ток и момент.

Если Р=0 (установившийся режим) I_д = I_с ;

М_д =М_с .

На кривых переходного процесса w = f(t) и

М_д = f(t) (Рис. 10-8.) наибольшее отклонение скорости Dw_дин от ее начального значения называют динамическим падением скорости, а статическую ошибку Dw_I — статическим падением скорости.

Отклонение характеризует перерегулирование по скорости, а отношение DМ_д /DМ _дуст — по моменту.

АСТАТИЧЕСКИЙ РЕГУЛЯТОР СКОРОСТИ

Рассмотрим характеристики САР скорости с ПИ- регулятором. Структурная схема аналогична рассмотренной ранее для статического регулятора скорости,передаточная функция регулятора:

Передаточные функции разомкнутых и замкнутых систем по управляющему воздействию.

где К_v =К_п К_д К_с /t_о — коэффициент усиления разомкнутой системы по w.

Из структурной схемы и передаточной функции следует, что регулятор скорости является астатической системой с астатизмом первого порядка, как по управляющему, так и по возмущающему I_с воздействиям. Следовательно: статические ошибки Dw_I и DU_e равны нулю, однако устойчивость системы ухудшается, т.к. интегратор вносит фазовый сдвиг в замкнутый контур- 90 о на всех частотах. Это так же следует из выражения для предельного коэффициента системы.

т.е. К_vпр имеет предельное значение. Оптимальное значение постоянной времени регулятора с точки зрения устойчивости t_Rотп = Т_э . В этом случае К_vпр = ¥.

Регулятор скорости с отрицательной обратной связь по току.

На рис представлена структурная схема САР с обратной связь по току.

К_т — коэффициент передачи ОС по току;

Т_т — постоянная времени фильтра/

Преобразуем структурную схему на рис к виду рис

Учитывая, что в статическом режиме р=0, I_д = I_с

,

(+)- при положительной обратной связи по току.

(-)- при отрицательной обратной связи по току.

Скорость идеального холостого хода в замкнутой и разомкнутой системах одинакова.

,

где Dw_р = I_с R_э К_д — падение скорости в разомкнутой системе.

На рис приведены статические характеристики w=f(I) для положительной а) ,

и для отрицательной б) ОС при U_з = const

К_т =0соответствует характеристике разомкнутой системы

При положительной обратной связи по току возможны три режима работы ЭП :

когда

В этом случае с ростом нагрузки скорость w уменьшается.

режим полной компенсации:

и Dw₃ = 0,

т.е. с изменением нагрузки w = const,

с ростом нагрузки скорость возрастает. Указанные режимы могут иметь место при К_т = const и при изменении К_р

При отрицательной обратной связи по току всегда, падение скорости под нагрузкой больше, чем в разомкнутой системе. Поэтому отрицательная обратная связь по току в регуляторах скорости применяется только в сочетании с отрицательной обратной связью по скорости.

Передаточные функции по задающему воздействию разомкнутой W(p) и замкнутой Ф(p) систем:

-для разомкнутой системы;

— для замкнутой системы;

Здесь «-» cоответствует положительной обратной связи по току;

«+» cоответствует отрицательной обратной связи по току;

При положительной обратной связи по току в режиме недокомпенсации система устойчива;

— в режиме перекомпенсации система не устойчива;

— в режиме компенсации система находится на границе устойчивости.

При отрицательной обратной связи система всегда устойчива.

Характер переходного процесса в системе зависит от коэффициента x₃ и W_03. Так как W_ор = W₀₃ , скорость затухания переходного процесса в замкнутой и разомкнутой системах одинакова. Если принять x_р = 1, тогда в режиме:

— недокомпенсации x₃ 1; переходной процесс апериодический.

Хотя в режиме недокомпенсации система устойчивости, регулятор скорости в таком режиме самостоятельно практического применения не получил; он широко используется совместно с отрицательной обратной связи по скорости в системах с повышенными требованиями к жесткости статической характеристики.

Для установившегося режима составим структурную схему (Рис. 10-14.).

В данном случае имеем систему стабилизации напряжения, подводимого к якорю ДПТ. Полагая выходным сигналом напряжение U_д , находим:

,

где Uдо — напряжение на входе ДПТ при I_с = 0

— падение напряжения в ТП в замкнутой системе при I_с > 0.

DU_др — падение напряжения в ТП в разомкнутой системе;

R_п — внутреннее сопротивление ТП;

К_н — коэффициент обратной связи по напряжению.

U_з выражения для DU_дз и DU_др видно, что падение напряжения в замкнутой системе при одинаковых I_с в (1+К_р К_п К_н ) раз меньше, чем в разомкнутой; замкнутая система обеспечивает стабилизацию напряжения U_д , компенсируя падение напряжения в силовой цепи преобразователя. Величина DU_дз является статической ошибкой по возмущению. При К = ¥ имеем идеальный источник питания неограниченной мощности и статическая характеристика регулятора будет представлять естественную характеристику ДПТ НВ (К = К_р К_п К_н ).

В общем случае статическая характеристика регулятора скорости:

Следовательно: обратная связь по напряжению не может быть использована для стабилизации w ЭП. Обычно она используется в регуляторах w в сочетании с другими видами обратных связей.

Динамические характеристики замкнутой системы авт. регулирования с отрицательной обратной связью по напряжению такие же как и в разомкнутой системе, т.е.