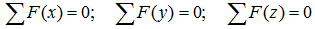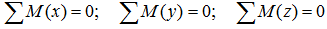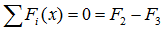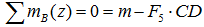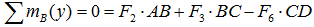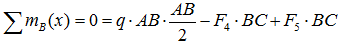Уравнение статики процессы и аппараты

iSopromat.ru

Уравнения равновесия (статики) характеризуют неподвижность заданной системы нагруженной комплексом внешних усилий.

При решении задач теоретической механики и сопротивления материалов (например, при определении опорных реакций или внутренних силовых факторов) исходя из условия неподвижности системы или ее частей, записываются уравнения равенства нулю сумм проекций всех сил на оси выбранной системы координат

что следует из условия отсутствия перемещения системы вдоль этих осей, и сумм моментов относительно произвольных точек системы

из условия отсутствия ее вращения относительно указанных осей.

Надо отметить что в случае действия плоской системы сил можно получить только три уравнения статики, а линейная схема нагружения позволяет записать лишь одно уравнение.

Пример составления уравнений равновесия

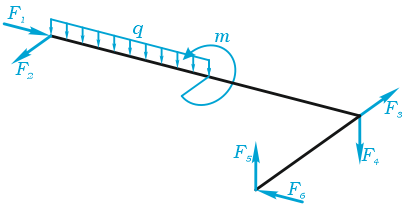
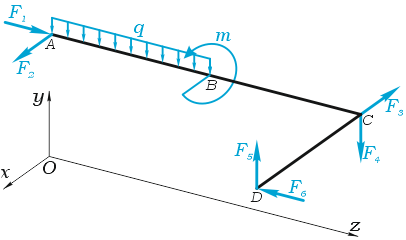
В качестве примера, рассмотрим общий случай пространственного нагружения, где комплекс усилий, включающий сосредоточенные силы F₁-F₆, равномерно распределенную нагрузку q, и момент m расположенный в плоскости перпендикулярной длинному стержню, удерживает L-образную систему в равновесии.

Обозначим характерные точки системы буквами A, B, C и D, зададим положение трехмерной системы координат xyz и запишем уравнения равновесия.

Суммы проекций сил

Сумма проекций всех сил на ось x (с учетом правила знаков для сил):

здесь при записи силы от распределенной нагрузки ее интенсивность q умножается на ее длину AB.

Суммы моментов

Суммы моментов всех нагрузок, например, относительно точки B (с учетом правила знаков для моментов):

• в плоскости xOy:
  
• в плоскости xOz:
  
• в плоскости yOz:
  

Из полученных шести уравнений можно определить не более шести неизвестных усилий.

Уважаемые студенты!
На нашем сайте можно получить помощь по техническим и другим предметам:
✔ Решение задач и контрольных
✔ Выполнение учебных работ
✔ Помощь на экзаменах

2. Математическое описание систем автоматического управления

Публикую первую часть второй главы лекций по теории автоматического управления.
В данной статье рассматриваются:

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях
2.2. Линеаризация уравнений динамики САУ (САР)
2.3. Классический способ решения уравнений динамики

Лекции по курсу «Управление Техническими Системами», читает Козлов Олег Степанович на кафедре «Ядерные реакторы и энергетические установки», факультета «Энергомашиностроения» МГТУ им. Н.Э. Баумана. За что ему огромная благодарность.

Данные лекции только готовятся к публикации в виде книги, а поскольку здесь есть специалисты по ТАУ, студенты и просто интересующиеся предметом, то любая критика приветствуется.

2.1. Получение уравнений динамики системы. Статическая характеристика. Уравнение динамики САУ (САР) в отклонениях

При составлении уравнений, описывающих нестационарные процессы в САУ (САР) и которые в дальнейшем будем называть уравнениями динамики, система “разбивается” на отдельные элементы (звенья), для каждого из которых не существует проблем в записи соответствующего уравнения динамики.

На рис. 2.1.1 представлено схематичное представление САУ (звена) в переменных «вход-выход», где x(t) (или u(t)) — входное воздействие, а y(t) — выходное воздействие, соответственно. Нередко входное воздействие будет называться управляющим, а выходное воздействие — регулируемой величиной (переменной).

При составлении уравнений динамики используются фундаментальные законы сохранения из разделов “Механики”, “Физики”, “Химии” и др.

Например, при описании перемещения узла какого-то механизма силового привода используются законы сохранения: момента, энергии, импульса и др… В теплофизических (теплогидравлических) системах используются фундаментальные законы сохранения: массы (уравнение неразрывности), импульса (уравнение движения), энергии (уравнение энергии) и др

Уравнения сохранения в общем случае содержат постоянные и нестационарные члены, причем при отбрасывании нестационарных членов получают так называемые уравнения статики, которые соответствуют уравнениям равновесного состояния САУ (звена). Вычитанием из полных уравнений сохранения стационарных уравнений получают нестационарные уравнения САУ в отклонениях (от стационара).

где: — стационарные значения входного и выходного воздействий;
— отклонения от станционара, соотвесвенно.

В качестве примера рассмотрим «технологию» получения уравнений динамики для механического демпфера, схематическое изображение которого представлено на рис. 2.1.2.

Согласно 2-му закону Ньютона, ускорение тела пропорционально сумме сил, действующих на тело:

где, m — масса тела, F_j — все силы воздействующие на тело (поршень демпфера)

Подставляя в уравнение (2.1.1) все силы согласно рис. 2.2, имеем:

где — сила тяжести; — сила сопротивления пружины, — сила вязконо трения (пропорциональна скорости поршеня)

Размерности сил и коэффициентов, входящих в уравнение (2.1.2):

Предполагая, что при t ≤ 0 поршень демпфера находился в равновесии, то есть

перейдем к отклонениям от стационарного состояния:
Пусть при t>0 . Тогда, подставляя эти соотношения в уравнение (2.1.2), получаем:

если , то уравнение принимает вид:

Соотношение (2.1.4) – уравнение звена (демпфера) в равновесном (стационарном) состоянии, а соотношение (2.1.5) – статическая характеристика звена – демпфера (см. рисунок 2.1.3).

Вычитая из уравнения (2.1.3) уравнение (2.1.4), получаем уравнение динамики демпфера в отклонениях:

тогда, разделив на k, имеем:

Уравнение (2.1.6) — это уравнение динамики в канонической форме, т.е. коэффициент при Δy(t) равен 1.0!

«Легко» видеть, что коэффициенты перед членами, содержащими производные, имеют смысл (и размерность!) постоянных времени. В самом деле:

Таким образом, получаем, что:
— коэффициент перед первой производной имеет размерность [c] т.е. смысл некоторой постоянной времени;
— коэффициент перед второй производной: [];
— коэффициент в правой части (): [].
Тогда уравнение (2.1.6) можно записать в операторной форме:

, что эквивалентно

где: — оператор диффренцирования;
-линейный дифференциальный оператор;
— линейный дифференциальный оператор, вырожденный в константу, равную .

Анализ уравнения (2.1.6.а) показывает, что такое уравнение имеет размерные переменные, а также размерными являются все коэффициенты уравнения. Это не всегда удобно. Кроме того, если реальная САР (САУ) состоит из многих звеньев, выходными воздействиями которых являются различные физические переменные (скорость, температура, нейтронный поток, тепловой поток и т.д.), то значения коэффициентов могут различаться на большое число порядков, что ставит серьезные математические проблемы при численном решении уравнений динамики на компьютере (поскольку числа в компьютере всегда представляются с какой-то точностью). Одним из наилучших способов избежать численных трудностей является принцип нормализации, т.е. переход к безразмерным отклонениям, которые получены нормированием отклонения на стационарное значение соответствующей переменной.

Введем новые нормированные (безразмерные) переменные:

Подставляя эти соотношения в уравнение (2.1.2), имеем:

Поддчеркнутые члены выражения в сумме дают 0 (см. 2.1.4) Перенося в левую часть члены, содержащие , и, разделив на , получаем:

где: — коэффициент усиления, причем безразмерный.

Проверим размерность коэффициента

Использованный выше «технический» прием позволяет перейти к безразмерным переменным, а также привести вид коэффициентов в уравнении динамики к легко интерпретируемому виду, т.е. к постоянным времени (в соответствующей степени) или к безразмерным коэффициентам усиления.

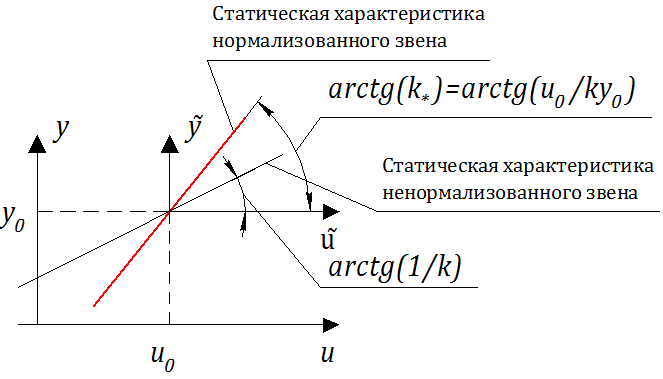
На рис. 2.1.4 представлены статические характеристики для механического демпфера:

Процедура нормировки отклонений позволяет привести уравнения динамики к виду:

где дифференциальные операторы.

Если дифференциальные операторы — линейные, а статическая характеристика САУ (звена) – тоже линейна, то выражение (2.1.8) соответствует линейному обыкновенному дифференциальному уравнению (ОДУ).

А если – нелинейные дифференциальные операторы, или , то уравнение динамики — нелинейное. Под нелинейными действиями понимаются все математические действия, кроме сложения (+) и вычитания (-).

Пример создания модели демпфера можно посмотереть здесь: «Технология получения уравнений динамики ТАУ»

2.2. Линеаризация уравнений динамики САУ (САР)

Практически все реальные системы автоматического управления (САУ) являются нелинейными, причем нелинейность САУ может определяться различными причинами:

1. Нелинейностью статической характеристики.
2. Нелинейностью динамических членов в уравнениях динамики.
3. Наличием в САУ принципиально нелинейных звеньев.

Если в замкнутой САУ (САР) нет принципиально нелинейных звеньев, то в большинстве случаев уравнения динамики звеньев, входящих в систему, могут быть линеаризованы. Линеаризация основана на том, что в процессе регулирования (т.е. САУ с обратной связью) все регулируемые величины мало отклоняются от их программных значений (иначе система регулирования или управления не выполняла бы своей задачи).

Например, если рассмотреть управление мощностью энергетического ядерного реактора, то главная задача САР — поддержание мощности на заданном (номинальном) уровне мощности. Существующие возмущения (внутренние и внешние) “отрабатываются” САР и поэтому параметры ядерного реактора незначительно отличаются от стационарных. На рис. 2.2.1 представлена временная зависимость мощности ядерного реактора, где нормированные отклонения мощности ΔN /N₀ Рис. 2.2.1 – Пример изменения мощности реактора

Рассмотрим некоторое звено (или САР в целом), описание динамики которого можно представить в переменных “вход-выход”:

Предположим, что динамика данного звена описывается обыкновенным дифференциальным уравнением n-го порядка:

Перенесем в левую часть уравнения и запишем уравнение в виде%

где -– функция регулируемой переменной и ее производных, а также управляющего (входного) воздействия и его производных, причем F – обычно нелинейная функция.

Будем считать, что при t ≤ 0 САУ (звено) находилось в равновесии (в стационарном состоянии). Тогда уравнение (2.2.2) вырождается в уравнение статической характеристики:

Разложим левую часть уравнения (2.2.2) в ряд Тейлора в малой окрестности точки равновесного состояния .

Напомним, что разложение в ряд Тейлора трактуется следующим образом: если , то «простое» разложение функции в ряд Тейлора в окрестности точки будет выглядеть так:

C учетом вышеприведенного разложение принимает вид:

Предполагая, что отклонения выходных и входных воздействий незначительны, (т.е.:), оставим в разложении только члены первого порядка малости (линейные). Поскольку , получаем:

Подставляя соотношение (2.2.4) в уравнение (2.2.2), и перенося множители при у и u в разные части получаем уравнения:

Коэффициенты — постоянные коэффициенты, поэтому уравнения 2.2.5 — линейное дифференциальное с постоянными коэффициентами.

В дальнейшем нами будет часто использоваться операторная форма записи уравнений динамики:

где – оператор дифференцирования;
— линейный дифференциальный оператор степени n;
— линейный дифференциальный оператор степени m, причем обычно порядок оператора выше порядка оператора :

Уравнения (2.2.5) и (2.2.6) — уравнения динамики системы (звена) в отклонениях.

Если исходное уравнение (2.2.1) — дифференциальное уравнение в физических переменных (температура, скорость, поток и т.д.), то размерность коэффициентов может быть произвольной (любой).

Переход к нормализованным отклонениям позволяет “упорядочить” размерность коэффициентов. В самом деле, разделив уравнение (2.2.5) на начальные условия (значения в нулевой момент времени) и выполнив некоторые преобразования, получаем:

Приведение уравнения динамики САУ (звена) к нормализованному виду позволяет “унифицировать” размерность коэффициентов уравнений: ==>

Если вынести в правой части (2.2.7) коэффициент за общую скобку и разделить все уравнение на , то уравнение принимает вид:

или в операторном виде:

Линеаризация уравнений динамики и нормализация переменных позволяют привести уравнения динамики САУ (звена) к виду, наиболее удобному для использования классических методов анализа, т.е. к нулевым начальным условиям.

Пример

Выполнить линеаризацию уравнения динамики некоторой «абстрактной» САР в окрестности состояния (x₀, y₀), если полное уравнение динамики имеет вид:

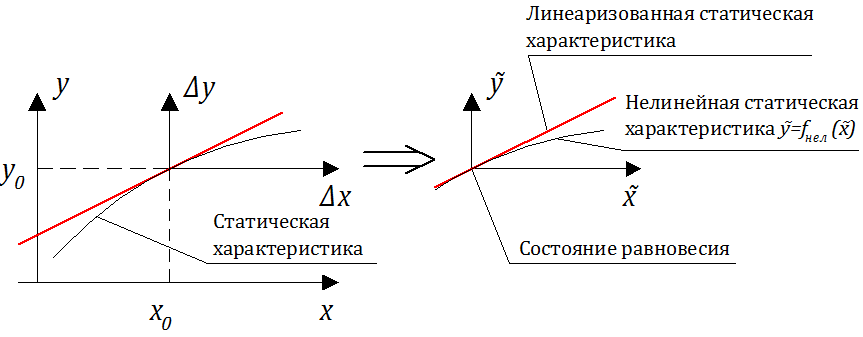
Нелинейность полного уравнения динамики проявляется в следующем:

• во-первых, в нелинейности статической характеристики:

• во-вторых, слагаемое в левой части — чисто нелинейное, так как действие умножения является нелинейным.

Выполним процесс линеаризации исходного уравнения, динамики без разложения я ряд Тейлора, основываясь на том, что в окрестности состояния (x₀, y₀) нормированные отклонения управляющего воздействия и регулируемой величины намного меньше 1.

Преобразования выполним в следующей последовательности:

1. Перейдем к безразмерным переменным (нормализованным);
2. Выполним линеаризацию, отбросив нелинейные члены 2-го и выше порядков малости.

Перейдем к новым безразмерным переменным:

Заметим, что:
.

Подставляя значения x(t) и y(t) в исходное уравнение:

Удаляем полученного уравнения уравнения стационара: , а так же пренебрегая слагаемыми второго прядка малости: , получаем следующее уравнение:

Вводим новые обозначения:

Получаем уравнения в «почти» классическом виде:

Если в правой части вынести за общую скобку и разделить все уравнение на , то уравнение (линеаризованное) принимает вид:

Процедура нормализации позволяет более просто линеаризовать уравнение динамики, так как не требуется выполнять разложение в ряд Тейлора (хотя это и не сложно).

2.3. Классический способ решения уравнений динамики

Классический метод решения уравнений динамики САУ (САР) применим только для линейных или линеаризованных систем.

Рассмотрим некоторую САУ (звено), динамика которой описывается линейным дифференциальным уравнением вида:

Переходя к полной символике, имеем:

Выражение (2.3.2) — обыкновенное дифференциальное уравнение (ОДУ), точнее неоднородное ОДУ, так как правая часть ≠ 0.

Известно входное воздействие x(t), коэффициенты уравнения и начальные условия (т.е. значения переменных и производных при t = 0).

Требуется найти y(t) при известных начальных условиях.

где: — решение однородного дифференциального уравнения y_<част.>(t) $inline$ — частное решение. $inline$

Будем называть решение однородного дифференциального уравнения , собственным решением, так как его решение не зависит от входного воздействия, а полностью определяется собственными динамическими свойствами САУ (звена).

Вторую составляющую решения (2.3.3) будем называть , вынужденным, так как эта часть решения определяется внешним воздействием , поэтому САУ (САР или звено) “вынуждена отрабатывать” это воздействие:

Напомним этапы решения:

1) Если имеется уравнение вида , то сначала решаем однородное дифференциальное уравнение:

2) Записываем характеристическое уравнение:

3) Решая уравнение (2.3.5), которое является типичным степенным уравнением, каким-либо способом (в том числе и с помощью стандартных подпрограмм на компьютере) находим корни характеристического уравнения
4) Тогда собственное решение записывается в виде:

если среди нет повторяющихся корней (кратность корней равна 1).

Если уравнение (2.3.5) имеет два совпадающих корня, то собственное решение имеет вид:

Если уравнение (2.3.5) имеет k совпадающих корней (кратность корней равна k), то собственное решение имеет вид:

5) Вынужденную часть решения можно найти различными способами, но наиболее распространены следующие способы:
а) По виду правой части.
б) Методом вариации постоянных.
в) Другие методы…

Если вид правой части дифференциального уравнения – относительно несложная функция времени, то предпочтительным является способ а): подбор решения. .

6) Суммируя полученные составляющие (собственную и вынужденную), имеем:

7) Используя начальные условия (t = 0), находим значения постоянных интегрирования . Обычно получается система алгебраических уравнений. Решая систему, находим значения постоянных интегрирования

Пример

Найти аналитическое выражение переходного процесса на выходе звена, если

Решение. Запишем однородное ОДУ:
Характеристическое уравнение имеет вид: ; Решая, имеем: тогда:

где — неизвестные (пока) постоянные интегрирования.

По виду временной функции в правой части запишем как:

Подставляя в исходное уравнение, имеем:

Суммируя , имеем:

Используя 1-е начальное условие (при t = 0), получаем: , а из 2-го начального условия имеем:

Решая систему уравнений относительно и , имеем:
Тогда окончательно:

Что бы проверить результ, выполним моделирование процесса в SimInTech, для этого преобразуем исходное уравнение к виду:

Создадим модель SimInTech, содержащую исходное динамическое уравнение и полученное аналитическое решение, и выведем результаты на один график (см. рис. 2.3.1).

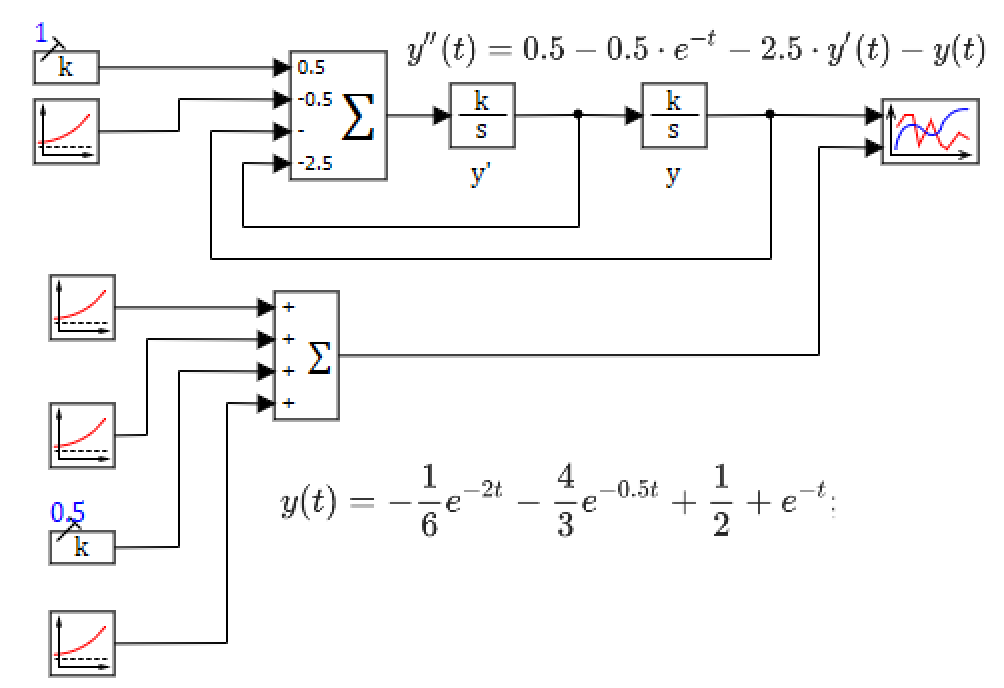
Рис. 2.3.1 – структурная схема для проверки решения

На рис. 2.3.2 приведено решение по вышеприведенному соотношению и численное решение задачи в среде SimInTech (решения совпадают и линии графиков «наложены» друг на друга).

Общие принципы расчета процессов и аппаратов

Расчеты процессов и aппаратов обычно имеют следующие основные пели: а) определение условий предельного, или равновесного состояния системы; б) вычисление расходов исходных материалов и количеств получаемых продуктов, а также количеств потребной энергии (тепла) и расхода теплоносителей; в) определение оптимальных режимов работы и рабочей поверхности аппаратов; г) вычисление основных размеров аппаратов.

Эти задачи определяют содержание и последовательность расчетов. Исходным этапом являются расчет и анализ статики процесса, т.е. рассмотрение данных о равновесии, на основе которых определяют направление протекания и возможные пределы осуществления процесса. Пользуясь этими данными, находят предельные значения параметров процесса, необходимые для вычисления его движущей силы. Затем составляются материальные и энергетические балансы исходя из законов сохранения массы и энергии. Затем рассчитывают кинетику процесса, определяющую скорость его протекания. По данным о скорости и величине движущей силы при выбранном оптимальном режиме работы аппарата находят его рабочую поверхность или объем. Зная величину поверхности или объема, определяют основные размеры аппарата.

Материальный баланс. По закону сохранения массы количество поступающих веществ ∑G_H должно быть равно количеству веществ ∑G_К, получаемых в результате проведения процесса: ∑G_H=∑G_К. Однако на практике неизбежны необратимые потери веществ, и тогда мат. баланса: ∑G_H=∑G_К +∑ G_П

Материальный баланс составляют для процесса в целом или для отдельных его стадий. Баланс может быть составлен для всех веществ, участвующих в процессе, и лишь для одного из веществ, многокомпонентной смеси. Например, материальный баланс процесса сушки составляют как по всему влажному материалу, поступающему на сушку, так и по одному из его компонентов — количеству абсолютно сухого вещества или количеству влаги, содержащейся в высушиваемом материале. Баланс составляют за единицу времени, например за 1 час,либо сутки (или за одну операцию в периодическом процессе) в расчете на единицу количества исходных или конечных продуктов.

На основе материального баланса определяют выход продукта, под которым понимают выраженное в процентах отношение полученного количества продукта к максимальному, т.е. теоретически возможному. Выход продукта обычно рассчитывают на единицу затраченного сырья. При наличии нескольких видов сырья выход выражают по отношению к какому-либо одному из них.

Имейте введу, что практический расход исходных материалов обычно превышает теоретический, так как химические реакции не протекают до конца, происходят потери реагирующих веществ (через неплотности аппаратуры и т.д.)

Энергетический баланс. Этот баланс составляют на основе закона сохранения энергии, согласно которому количество энергии, введенной в процесс, равно количеству выделившейся энергии, т.е. приход энергии равен ее расходу. Проведение химико-технологических процессов обычно связано с затратой различных видов энергии — механической, электрической и др. Эти процессы часто сопровождаются изменением энтальпии системы вследствие изменения агрегатного состояния веществ (испарения, конденсации, плавления и т.д.). В химических процессах очень большое значение может иметь тепловой эффект протекающих реакций.

Частью энергетического баланса является тепловой баланс, который в общем виде выражается уравнением ∑Q_H=∑Q_К +∑ Q_П

где Q_{1 —} тепло, вводимое с исходными веществами; Q₂ — количество тепла, подводимого извне, например с теплоносителем, обогревающим аппарат; Q₃ — тепловой эффект физических или химических превращений (если тепло в ходе процесса поглощается, то этот член входит с отрицательным знаком).

Количество отводимого тепла∑Q_К складывается из тепла, удаляющегося с конечными продуктами, и отводимого с теплоносителем (например, с охлаждающим агентом).

В энергетическом балансе, кроме тепла, учитываются приход и расход всех видов энергии, например затраты механической энергии на перемещение жидкостей или сжатие и транспортирование газов.

На основании теплового баланса находят расход водяного пара, воды и других теплоносителей, а по данным энергетического баланса общий расход энергии на осуществление процесса.

Интенсивность процессов и аппаратов. Для анализа и расчета процессов химической технологии необходимо, кроме данных материального и энергетического балансов, знать интенсивность процессов и аппаратов.

Все основные процессы (гидродинамические, тепловые, массообменные) могут протекать только под действием некоторой движущей силы, которая для гидромеханических процессов определяется разностью давлений, для теплообменных разностью температур, для массообменных — разностью концентраций вещества.

В первом приближении можно считать, что результат процесса, характеризуемый, например, количеством Мперенесенного вещества или тепла, пропорционален движущей силе (обозначаемой в общем виде через Δ), времени τ и некоторой величине А, к которой относят интенсивность процесса. Такой величиной может быть рабочая поверхность, через которую происходит перенос энергии или массы, рабочий объем, в котором осуществляется процесс, и т.д. Следовательно, уравнение любого процесса может быть представлено в общем виде:

Коэффициент пропорциональности Кхарактеризует скорость процесса и, таким образом, представляет собой кинетический коэффициент, или коэффициент скорости процесса (коэффициент теплопередачи, коэффициент массоперсдачи и т. д.). Коэффициент Котражает влияние всех факторов, не учтенных величинами, входящими в правую часть уравнения, а также все отклонения реального процесса от этой упрощенной зависимости.

Под интенсивностью процесса понимают его результат, отнесенный к единице времени и единице величины A, т.е. количество энергии или массы, перешедшей вединицу времени через единицу рабочей поверхности

Соответственно величину Кможно рассматривать как меру интенсивности процесса — интенсивность, отнесенную к единице движущей силы. Интенсивность процесса всегда пропорциональна движущей силе Δ, и обратно пропорциональна сопротивлению R, которое является величиной, обратной кинетическому коэффициенту (например, гидравлическое сопротивление, термическое сопротивление, сопротивление массопередаче и т. д.). Таким образом, уравнение (1) может быть выражено также в форме: M= A Δ∙τ / R (2)

Из уравнения (1) или (2) находят необходимую рабочую поверхность или рабочий объем аппарата по известным остальным величинам, входящим в уравнение, или определяют результат процесса при заданной поверхности или объеме.

От интенсивности процесса следует отличать объемную интенсивность аппарата — интенсивность, отнесенную к единице его общего объема. С увеличением объемной интенсивности уменьшаются размеры аппарата и снижается расход материалов на его изготовление. Однако объемная интенсивность может лишь до определенной степени служить мерой совершенства аппарата. Это объясняется тем, что объемная интенсивность аппарата связана с интенсивностью процесса, но с увеличением коэффициента скорости процесса его интенсивность обычно возрастает лишь до какого-то известного предела. Увеличение коэффициента скорости сверх этой величины часто сопровождается уменьшением движущей силы, что может привести к прекращению увеличения интенсивности процесса.

При оценке конструкции аппарата или режима его работы решающее значение должны иметь технико-экономические характеристики данного аппарата. Оптимальным будет такой аппарат (или такой режим его работы), который обеспечит заданный результат с наименьшими затратами.

Затраты на осуществление процесса складываются нз капитальных затрат и эксплуатационных расходов.

Определение основных размеров аппаратов. Пользуясь уравнением (1) вычисляют основные размеры непрерывно действующего аппарата. Если известен объем среды, протекающей через аппарат в единицу времени и V_сек и задана ее линейная скорость w, то площадь поперечного сечения S аппарата находят из следующего соотношения:

По величине S определяют один из основных размеров аппарата, например для аппарата цилиндрической формы — его диаметр D. Другим основным размером является рабочая высота (или длина) аппарата. Из уравнения (1) находят рабочий объем аппарата или поверхность F, требуемую для проведения процесса. Зная Fи пользуясь зависимостью F = a∙V, где аповерхность, приходящаяся на единицу объема аппарата (удельная поверхность), рассчитывают его рабочий объем. По величине V определяют высоту H, применяя соотношение V = SH. Рабочий объем V периодически действующего аппарата определяют как произведение заданной производительности и периода процесса τ_сек. включающего продолжительность самого процесса, а также время, затрачиваемое на загрузку, выгрузку и другие вспомогательные операции.

Моделирование и оптимизация процессов и аппаратов. Исследование процессов и аппаратов в масштабах и условиях промышленного производства является сложным, длительным и дорогостоящим. В связи с этим большое значение имеет моделирование — изучение закономерностей процессов на моделях при условиях, допускающих распространение полученных результатов на все процессы, подобные изученному, независимо от масштаба аппарата.

Общие принципы моделирования вытекают из теории подобия. Согласно требованиям этой теории должны соблюдаться следующие правила моделирования:

1) необходимо, чтобы процессы в модели и в самом рабочем аппарате (оригинале) описывались одинаковыми дифференциальными уравнениями;

2) модель должна быть геометрически подобна оригиналу;

3) численные значении начальных и граничных условий, выраженных в безразмерной форме, для модели и оригинала должны быть равны;

4) необходимо, чтобы все безразмерные комплексы физических и геометрических величин, влияющих на процесс (критерии подобия), были равны во всех сходственных точках модели и оригинала.

Если последнее требование невыполнимо и протекание процесса практически мало зависит от тех или иных критериев подобия, то равенством их в модели и оригинале пренебрегают, проводя приближенное моделирование.

Моделирование процессов можно также осуществлять на основе математической аналогии одинаковой формы уравнений, описывающих физически различные явления. При использовании компьютерных технологий математическое моделирование позволяет значительно ускорить исследование наиболее сложных процессов химической технологии.

Заключительным этапом моделирования процессов является их оптимизация, выбор оптимальных условий проведения процесса. Определение этих условий связано с выбором критерия оптимизации, который может зависеть от оптимальных значений ряда параметров (например, температуры, давления, степени извлечения и др.) Между параметрами обычно существует сложная взаимосвязь, что сильно затрудняет выбор единого критерия, всесторонне характеризующего эффективность процесса. Задача сводится к поиску экстремального значения (минимума или максимума) целевой функции, выражающей зависимость величины выбранного критерия оптимизации от влияющих на него факторов.