Ромб. Формулы, признаки и свойства ромба
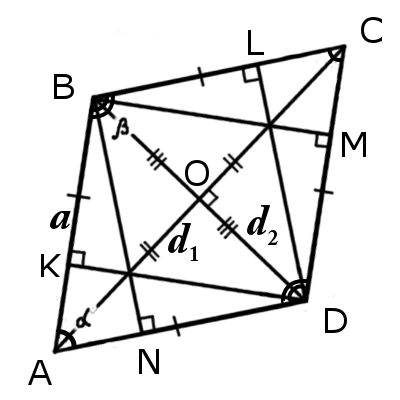 | 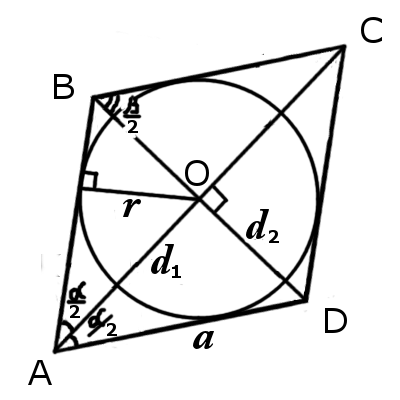 |
| Рис.1 | Рис.2 |
Признаки ромба
∠BAC = ∠CAD или ∠BDA = ∠BDC
Δ ABO = Δ BCO = Δ CDO = Δ ADO
Основные свойства ромба
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
AC 2 + BD 2 = 4AB 2
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
| a = | S |
| ha |
2. Формула стороны ромба через площадь и синус угла:
| a = | √ S |
| √ sinα |
| a = | √ S |
| √ sinβ |
3. Формула стороны ромба через площадь и радиус вписанной окружности:
| a = | S |
| 2 r |
4. Формула стороны ромба через две диагонали:
| a = | √ d 1 2 + d 2 2 |
| 2 |
5. Формула стороны ромба через диагональ и косинус острого угла ( cos α ) или косинус тупого угла ( cos β ):
| a = | d 1 |
| √ 2 + 2 cosα |
| a = | d 2 |
| √ 2 — 2 cosβ |
6. Формула стороны ромба через большую диагональ и половинный угол:
| a = | d 1 |
| 2 cos ( α /2) |
| a = | d 1 |
| 2 sin ( β /2) |
7. Формула стороны ромба через малую диагональ и половинный угол:
| a = | d 2 |
| 2 cos ( β /2) |
| a = | d 2 |
| 2 sin ( α /2) |
8. Формула стороны ромба через периметр:
| a = | Р |
| 4 |
Диагонали ромба
Формулы определения длины диагонали ромба:
d 1 = a √ 2 + 2 · cosα
d 1 = a √ 2 — 2 · cosβ
d 2 = a √ 2 + 2 · cosβ
d 2 = a √ 2 — 2 · cosα
d 1 = 2 a · cos ( α /2)
d 1 = 2 a · sin ( β /2)
d 2 = 2 a · sin ( α /2)
d 2 = 2 a · cos ( β /2)
7. Формулы диагоналей через площадь и другую диагональ:
| d 1 = | 2S |
| d 2 |
| d 2 = | 2S |
| d 1 |
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
| d 1 = | 2 r |
| sin ( α /2) |
| d 2 = | 2 r |
| sin ( β /2) |
Периметр ромба
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Площадь ромба
Формулы определения площади ромба:
4. Формула площади ромба через две диагонали:
| S = | 1 | d 1 d 2 |
| 2 |
5. Формула площади ромба через синус угла и радиус вписанной окружности:
| S = | 4 r 2 |
| sinα |
6. Формулы площади через большую диагональ и тангенс острого угла ( tgα ) или малую диагональ и тангенс тупого угла ( tgβ ):
| S = | 1 | d 1 2 · tg ( α /2) |
| 2 |
| S = | 1 | d 2 2 · tg ( β /2) |
| 2 |
Окружность вписанная в ромб
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
| r = | h |
| 2 |
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
| r = | S |
| 2 a |
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
| r = | √ S · sinα |
| 2 |
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
| r = | a · sinα |
| 2 |
| r = | a · sinβ |
| 2 |
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
| r = | d 1 · sin ( α /2) |
| 2 |
| r = | d 2 · sin ( β /2) |
| 2 |
6. Формула радиуса круга вписанного в ромб через две диагонали:
| r = | d 1 · d 2 |
| 2√ d 1 2 + d 2 2 |
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
| r = | d 1 · d 2 |
| 4 a |
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.
Сторона ромба онлайн
С помощю этого онлайн калькулятора ромба можно найти длину стороны ромба по известным элементам. Для нахождения стороны ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.
| Открыть онлайн калькулятор |
1. Сторона ромба через высоту и площадь
Пусть известны площадь и высота ромба (Рис.1).
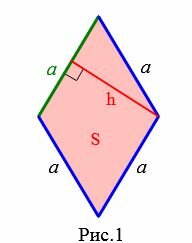 |
Покажем, что сторона ромба через высоту и площадь вычисляется формулой
| \(\small a=\frac<\large S><\large h>.\) | (1) |
Формула площади ромба через сторону и высоту имеет следующий вид:
| \(\small S=a \cdot h.\) |
Откуда легко вывести формулу (1).
2. Сторона ромба через высоту и угол
Рассмотрим ромб с высотой h и углом α между сторонами (Рис.2). Выведем формулу вычисления стороны ромба через высоту и угол.
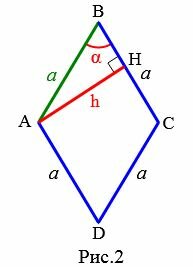 |
Для прямоугольного треугольника AHB применим теорему синусов:
| \(\small \frac<\large a><\large \sin 90°>=\frac<\large h><\large \sin \alpha>.\) |
Откуда получим формулу вычисления высоты ромба через сторону и угол между сторонами:
| \(\small a=\frac<\large h><\large \sin \alpha>.\) | (2) |
Заметим, что формула (2) справедлива для любого угла ромба, как для острого, так и для тупого. Действительно. Из четвертого свойста ромба (см. статью Ромб) следует, что сумма соседних углов ромба равна 180°. Тогда для угла C можно записать: \(\small \angle C=180°-\alpha.\) Следовательно \(\small \sin \angle C=\sin(180°-\alpha)=\sin \alpha.\) Получили, что синусы углов ромба равны. Поэтому в качестве угла между сторонами ромба можно выбрать любой угол ромба.
3. Сторона ромба через диагонали
Выведем формулу вычисления сторон ромба через диагонали.
Выразим сторону a ромба через диагонали. Поскольку диагонали ромба перпендикулярны и делятся пополам точкой их пересечения (свойства 5 и 6 ромба), то диагонали делят ромб на четыре равных прямоугольных треугольника (Рис.3).
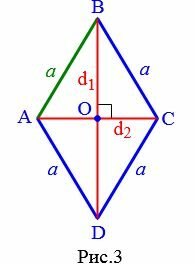 |
Применим к прямоугольному треугольнику AOB теорему Пифагора:
| \(\small a^2= \left( \frac<\large d_1> <\large 2>\right)^2+\left( \frac<\large d_2> <\large 2>\right)^2.\) |
| \(\small a= \frac<\sqrt<\large d_1^2+d_2^2>> <\large 2>\) | (3) |
4. Сторона ромба через угол и противолежащую диагональ
Пусть известны один из углов α=∠ABC ромба и противолежащая диагональ d=AC (Рис.4). Выведем формулу вычисления сторон ромба.
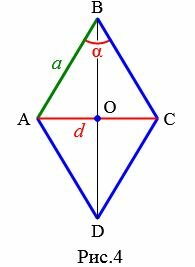 |
Проведем другой диагональ BD. Как было отмечено выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Кроме этого, диагонали ромба делят углы ромба пополам. Применим теорему синусов для прямоугольного треугольника AOB:
| \(\small \frac<\large a><\large \sin 90°>=\frac<\large \frac |
Откуда получим формулу стороны ромба через угол и противолежащую диагональ:
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \sin \frac< \alpha>< 2>>.\) | (4) |
Формулу (4) можно записать и в другом виде, применяя формулу синуса половинного угла:
| \(\small \sin \frac< \alpha>< 2>=\sqrt<\frac<\large 1-\cos \alpha><\large 2 >>.\) | (5) |
Подставляя (5) в (4), получим:
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \sqrt<\frac<\large 1-\cos \alpha><\large 2 >>>.\) |
| \(\small a=\large \frac< d>< \sqrt< 2-2 \ \cdot \ \cos \alpha>>.\) | (6) |
5. Сторона ромба через угол и диагональ из данного угла
Пусть известны один из углов α=∠ABC ромба и диагональ из данного угла d=BD (Рис.5). Выведем формулу вычисления высоты ромба.
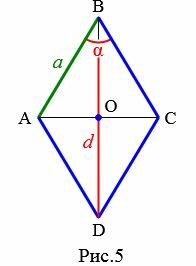 |
Проведем другой диагональ AC. Как было отмечено в выше, диагонали ромба перпендикулярны и делятся пополам точкой их пересечения. Для прямоугольного треугольника AOB, имеем:
| \(\small \frac<\large OB > <\large a>=\cos \angle ABO.\) | (7) |
Учитывая, что \( \small BO=\frac<\large d><\large 2>\) и \( \small \angle ABO=\frac<\large \alpha><\large 2>\), формулу (13) можно записать так:
| \(\small \frac< \large \frac<\large d > <\large 2>><\large a>= \cos \frac<\large \alpha> <\large 2>.\) |
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \cos \large \frac< \alpha>< 2>>.\) | (8) |
Формулу (8) можно записать и в другом виде, применяя формулу косинуса половинного угла:
| \(\small \cos \frac< \alpha>< 2>=\sqrt<\frac<\large 1+\cos \alpha><\large 2 >>.\) | (9) |
Подставляя (9) в (8), получим:
| \(\small a=\frac<\large d><\large 2 \ \cdot \ \sqrt<\frac<\large 1+\cos \alpha><\large 2 >>>.\) |
| \(\small a=\large \frac< d>< \sqrt< 2+2 \ \cdot \ \cos \alpha>>.\) | (10) |
6. Сторона ромба через площадь и радиус вписанной в ромб окружности
В статье Площадь ромба показали, что площадь ромба через сторону и радиус вписанной в ромб окружности вычисляется формулой
| \(\small S= 2 \cdot a \cdot r.\) | (11) |
Из формулы (11) получим:
| \( \small a=\frac<\large S> <\large 2 \ \cdot \ r>\) | (12) |
7. Сторона ромба через площадь и угол
В статье Площадь ромба показали, что площадь ромба через сторону и угол вычисляется формулой
| \(\small S= a^2 \cdot \sin \alpha.\) | (13) |
Из формулы (13) найдем a:
| \( \small a=\frac<\large S> <\large \sin \alpha>\) | (14) |
Получили формулу сторон ромба через площадь и угол.
Графический метод решения задач с параметрами
Теперь вы узнали, что такое параметр, и увидели решение самых простых задач.
Но подождите — рано успокаиваться и говорить, что вы все знаете. Есть множество типов задач с параметрами и приемов их решения. Чтобы чувствовать себя уверенно, мало посмотреть решения трех незатейливых задач.
Вот список тем, которые стоит повторить:
1. Элементарные функции и их графики. Парабола, синус, логарифм, арктангенс и все остальные — всех их надо знать «в лицо».
Только после этого можно переходить к самому простому и наглядному способу решения задач с параметрами — графическому. Конечно, он не единственный. Но начинать лучше всего именно с него.
Мы разберем несколько самых простых задач, решаемых графическим методом. Больше задач — в видеокурсе «Графический метод решения задач с параметрами» (бесплатно).
1. При каких значениях параметра a уравнение имеет ровно 2 различных решения?
Дробь равна нулю тогда и только тогда, когда ее числитель равен нулю, а знаменатель не равен нулю.
В первом уравнении выделим полный квадрат:
Это уравнение окружности с центром в точке и радиусом равным 2. Обратите внимание — графики будем строить в координатах х; а.
Уравнение задает прямую, проходящую через начало координат. Нам нужны ординаты точек, лежащих на окружности и не лежащих на этой прямой.
Для того чтобы точка лежала на окружности, ее ордината а должна быть не меньше 0 и не больше 4.
Кроме того, точка не должна лежать на прямой , которая пересекает окружность в точках и Координаты этих точек легко найти, подставим в уравнение окружности.
Точка С также не подходит нам, поскольку при мы получим единственную точку, лежащую на окружности, и единственное решение уравнения.
2. Найдите все значения a, при которых уравнение имеет единственное решение.
Уравнение равносильно системе:
Мы возвели обе части уравнения в квадрат при условии, что (смотри тему «Иррациональные уравнения»).
Раскроем скобки в правой части уравнения, применяя формулу квадрата трехчлена. Получаем систему.
Приводим подобные слагаемые в уравнении.
Заметим, что при прибавлении к правой и левой части числа 49 можно выделить полные квадраты:
Решим систему графически:
Уравнение задает окружность с центром в точке , где радиус
Неравенство задает полуплоскость, которая расположена выше прямой , вместе с самой этой прямой.
Исходное уравнение имеет единственное решение, если окружность имеет единственную общую точку с полуплоскостью. Другими словами, окружность касается прямой, заданной уравнением
Пусть С — точка касания.
На координатной плоскости отметим точки и , в которых прямая пересекает оси Y и Х.
Рассмотрим треугольник ABP. Он прямоугольный, и радиус окружности PC является медианой этого треугольника. Значит по свойству медианы прямоугольного треугольника, проведенной к гипотенузе.
Из треугольника ABP найдем длину гипотенузы AB по теореме Пифагора.
Решая это уравнение, получаем, что
3. Найдите все положительные значения параметра а, при каждом из которых система имеет единственное решение.
График уравнения — окружность с центром и радиусом равным 2.
График уравнения — две симметричные окружности и радиуса 2 c центрами в точках и
Второе уравнение при задает окружность с центром в точке и радиусом a.
Вот такая картинка, похожая на злую птицу. Или на хрюшку. Кому что нравится.
Система имеет единственное решение в случаях, когда окружность , задаваемая вторым уравнением, касается только левой окружности или только правой
Если a — радиус окружности , то это значит, что (только правая) или (только левая).
Пусть А — точка касания окружности и окружности
, (как гипотенуза прямоугольного треугольника МNР с катетами 3 и 4),
В — точка касания окружности и окружности
длину MQ найдем как гипотенузу прямоугольного треугольника KMQ с катетами 7 и 4; Тогда для точки В получим:
Есть еще точки С и D, в которых окружность касается окружности или окружности соответственно. Однако эти точки нам не подходят. В самом деле, для точки С:
, но и это значит, что окружность с центром в точке М, проходящая через точку С, будет пересекать левую окружность и система будет иметь не одно, а три решения.
Аналогично, для точки D:
и значит, окружность с центром М, проходящая через точку D, будет пересекать правую окружность и система будет иметь три решения.
4. При каких значениях a система уравнений имеет 4 решения?
Конечно же, решаем графически. Только непуганый безумец возьмется решать такую систему аналитически : -)
И в первом, и во втором уравнении системы уже можно разглядеть известные «базовые элементы» (ссылка) — в первом ромбик, во втором окружность. Видите их? Как, еще нет? — Сейчас увидите!
Просто выделили полный квадрат во втором уравнении.
Сделаем замену Система примет вид:
Вот теперь все видно! Рисовать будем в координатах
Графиком первого уравнения является ромб, проходящий через точки с координатами и
Графиком второго уравнения является окружность с радиусом и центром в начале координат.
Когда же система имеет ровно 4 решения?
1) В случае, когда окружность вписана в ромб, то есть касается всех сторон ромба.
Запишем площадь ромба двумя способами — как произведение диагоналей пополам и как произведение стороны на высоту, проведенную к этой стороне.
Диагонали нашего ромба равны 8 и 6. Значит,
Сторону ромба найдем по теореме Пифагора. Видите на рисунке прямоугольный треугольник со катетами 3 и 4? Да, это египетский треугольник, и его гипотенуза, то есть сторона ромба, равна 5. Если h — высота ромба, то

Мы получили ответ:
2) Есть второй случай, и мы его найдем.
Давайте посмотрим — если уменьшить радиус окружности, сделав , окружность будет лежать внутри ромба, не касаясь его сторон. Система не будет иметь решений, и нам это не подходит.
Пусть радиус окружности больше, чем , но меньше 3. Окружность дважды пересекает каждую из четырех сторон ромба, и система имеет целых 8 решений. Опять не то.
Пусть радиус окружности равен 3. Тогда система имеет 6 решений.
А что, если ? Окружность пересекает каждую сторону ромба ровно 1 раз, всего 4 решения. Подходит!
Значит, Объединим случаи и запишем ответ:
Больше задач и методов решения — на онлайн-курсе Анны Малковой. И на интенсивах ЕГЭ-Студии в Москве.
http://matworld.ru/geometry/storona-romba.php
http://ege-study.ru/graficheskij-metod-resheniya-zadach-s-parametrami/




