Уравнение стоячей волны для струны

Стоячие волны: формулы, характеристики, виды, примеры

Стоячие волны: формулы, характеристики, виды, примеры — Наука

Содержание:

В стоячие волны Это волны, которые распространяются в ограниченной среде, движутся и приходят в части пространства, в отличие от бегущих волн, которые при распространении удаляются от источника, который их породил, и не возвращаются к нему.

Они являются основой звуков, производимых музыкальными инструментами, поскольку легко возникают в закрепленных струнах либо на одном, либо на обоих концах. Они также создаются на плотных мембранах, таких как барабаны, или внутри труб и конструкций, таких как мосты и здания.

Когда у вас есть фиксированная струна на обоих концах, например, у гитары, создаются волны с одинаковой амплитудой и частотой, которые распространяются в противоположных направлениях и объединяются, создавая явление, называемое вмешательство.

Если волны синфазны, пики и впадины выровнены и в результате получается волна с удвоенной амплитудой. В таком случае мы говорим о конструктивном вмешательстве.

Но если мешающие волны не совпадают по фазе, пики одной встречаются с впадинами других, и результирующая амплитуда равна нулю. Тогда речь идет о деструктивном вмешательстве.

Формулы и уравнения

Основными элементами волны, представляющей ее в пространстве и времени, являются ее амплитуда A, длина волны λ и угловая частота ω.

В математическом представлении предпочтительнее использовать k, чем волновое число или количество раз, когда волна встречается на единицу длины. Поэтому он определяется длиной волны λ, которая представляет собой расстояние между двумя долинами или двумя гребнями:

В то время угловая частота относится к периоду или продолжительности полного колебания, например:

А также частота f определяется как:

Также волны движутся со скоростью v в соответствии:

Математическое выражение стоячей волны

Математически мы можем выразить волну синусоидальной функцией или косинусоидальной функцией. Предположим, что у нас есть волны одинаковой амплитуды A, длины волны λ и частоты ω, распространяющиеся вдоль струны и в противоположных направлениях:

Y₁ = A sin (kx — ωt)

При их добавлении находим получившуюся волну и_р:

Y_р = и₁ + и₂ = A sin (kx — ωt) + A sin (kx + ωt)

Чтобы найти сумму, существует тригонометрическое тождество:

грех α + грех β = 2 греха (α + β) / 2. cos (α — β) / 2

По этому тождеству результирующая волна y_р осталось:

Y_р = [2A sin kx]. cos ωt

Расположение узлов и брюшков

Результирующая волна имеет амплитуду A_р = 2Asen kx, который зависит от положения частицы. Тогда в точках, для которых sin kx = 0, амплитуда волны обращается в нуль, т. Е. Отсутствует вибрация.

Поскольку k = 2 π / λ:

(2 π / λ) x = π, 2π, 3π…

х = λ / 2, λ, 3λ / 2 .

В таких местах происходит деструктивная интерференция, которая называется узлы. Они разделены расстоянием, равным λ / 2, как следует из предыдущего результата.

А между двумя последовательными узлами находятся пучности или животы, в котором амплитуда волны максимальна, так как там происходит конструктивная интерференция. Они возникают при:

kx = ± π / 2, 3π / 2, 5π / 2…

Снова k = 2 π / λ и тогда:

x = λ / 4, 3λ / 4, 5λ / 4,…

Нормальные режимы на струне

Граничные условия в струне определяют, каковы длины волн и частоты. Если струна длины L закреплена на обоих концах, она не может вибрировать ни на какой частоте, потому что точки, в которых закреплена струна, уже являются узлами.

Кроме того, расстояние между соседними узлами составляет λ / 2, а между узлом и животом λ / 4, таким образом, только для определенных длин волн создаются стационарные волны: те, в которых целое число n из λ / 2 помещается в из:

(λ / 2) = L, где n = 1, 2, 3, 4….

Гармоники

Различные значения, которые принимает λ, называются гармоники. Таким образом, мы имеем:

-Первая гармоника: λ = 2L

-Вторая гармоника: λ = L

-Третья гармоника: λ = 2 L / 3

-Четвертая гармоника: λ = L / 2

Скорость и частота

Хотя кажется, что стоячая волна не движется, уравнение остается в силе:

Теперь можно показать, что скорость, с которой волна распространяется в струне, зависит от натяжения T в ней и ее линейной плотности массы μ (массы на единицу длины) как:

Характеристики стоячих волн

-Когда волны неподвижны, результирующая волна не распространяется так же, как ее компоненты, которые переходят из одной стороны в другую. Есть точки, где y = 0, потому что нет вибрации: узлы, другими словами, амплитуда A_р он становится нулевым.

-Математическое выражение стоячей волны состоит из произведения пространственной части (которая зависит от координаты x или пространственных координат) и временной части.

-Между узлами результирующая черная волна колеблется в одном месте, в то время как волны, которые переходят из одной стороны в другую, не совпадают по фазе там.

-Энергия не переносится точно в узлах, так как она пропорциональна квадрату амплитуды, но задерживается между узлами.

-Расстояние между соседними узлами составляет половину длины волны.

-Точки, в которых закреплена веревка, также считаются узлами.

Типы

Стоячие волны в одном измерении

Волны в неподвижной струне — это примеры стоячих волн в одном измерении, математическое описание которых мы предложили в предыдущих разделах.

Стоячие волны в двух и трех измерениях

Стоячие волны также могут быть представлены в двух и трех измерениях, поскольку их математическое описание немного сложнее.

Примеры стоячих волн

Фиксированные веревки

— Фиксированный трос на одном конце, который колеблется вручную или с помощью поршня на другом, генерирует стоячие волны по всей своей длине.

Музыкальные инструменты

-При игре на струнных инструментах, таких как гитара, арфа, скрипка и фортепиано, также возникают стоячие волны, так как струны имеют разное натяжение и закреплены на обоих концах.

Стоячие волны также создаются в трубках с воздухом, например в органах.

Здания и мосты

Стоячие волны возникают в таких конструкциях, как мосты и здания. Примечательным случаем стал подвесной мост Tacoma Narrows около города Сиэтл, США. Вскоре после открытия в 1940 году этот мост рухнул из-за стоячих волн, созданных ветром внутри.

Частота ветра была соединена с собственной частотой моста, создавая в нем стоячие волны, амплитуда которых увеличивалась, пока мост не рухнул. Это явление известно как резонанс.

Сейш

В портах есть очень любопытное явление под названием сейша, в котором морские волны производят большие колебания. Это связано с тем, что воды в порту довольно замкнутые, хотя океанические воды время от времени проникают через вход в порт.

Воды порта движутся со своей частотой, как и воды океана. Если обе воды равны по своим частотам, большая стоячая волна создается резонансом, как это произошло с мостом Такома.

В сейши Они также могут встречаться в озерах, водохранилищах, бассейнах и других водоемах с ограниченной поверхностью.

Аквариумы

Стоячие волны могут возникать в аквариуме, который несет человек, если частота, с которой человек ходит, равна частоте колебаний воды.

Упражнение решено

Струна гитары имеет L = 0,9 м и линейную массовую плотность μ = 0,005 кг / м. Он подвергается натяжению 72 Н, и его режим колебаний соответствует показанному на рисунке, с амплитудой 2А = 0,5 см.

а) Скорость распространения

б) Частота волны

в) Соответствующее уравнение стоячей волны.

Решение для

v = [72 Н / (0,005 кг / м)] 1/2 = 120 м / с.

Решение б

Расстояние между двумя соседними узлами λ / 2, поэтому:

(2/3) L — (1/3) L = λ / 2

λ = 2L / 3 = 2 x 0,90 м / 3 = 0,60 м.

Поскольку v = λ.f

f = (120 м / с) / 0,60 м = 200 с -1 = 200 Гц.

Решение c

Y_р = [2A sin kx]. cos ωt

Нам нужно подставить значения:

k = 2π / λ = k = 2π / 0,60 м = 10 π / 3

ω = 2π x 200 Гц = 400 π Гц.

Амплитуда 2А уже дается выражением:

2А = 0,5 см = 5 х 10 -3 м.

Y_р = 5 х 10 -3 м. грех [(10π / 3) х]. cos (400πt) =

= 0,5 см. грех [(10π / 3) х]. cos (400πt)

Ссылки

1. Бауэр, В. 2011. Физика для инженерии и науки. Том 1. Мак Гроу Хилл.
2. Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 7. Волны и квантовая физика. Отредактировал Дуглас Фигероа (USB).
3. Джанколи, Д. 2006. Физика: принципы с приложениями. 6-е. Эд Прентис Холл.
4. Сервей, Р., Джуэтт, Дж. (2008). Физика для науки и техники. Том 1. 7-е. Под ред. Cengage Learning.
5. Типлер П. (2006) Физика для науки и техники. 5-е изд., Том 1. От редакции Reverté.
6. Википедия. Seiche. Получено с: es.wikipedia.org.

Неверность: причины и последствия

Суксидин: применение и побочные эффекты этого препарата

Стоячие волны на струне

Изучите процесс формирования стоячей волны в струне: определение стоячей волны и частота, конструктивные и деструктивные помехи, особенности колебания в струне.

Стоячая волна образуется из-за помех при отражении поперечных волн в струнах.

Задача обучения

• Определить, когда формируется стоячая волна.

Основные пункты

• Отраженная волна инвертируется от падающей, когда поперечная на струне закрепляется в финальной точке. Отраженная не инвертируется от падающей, если поперечная в финальной точке свободна.
• Стоячая волна возникает, если падающая встречает отраженную на струне.
• В стоячей волне есть узлы и пучности.
• Каждая точка колеблется вверх и вниз, а амплитуда зависит от их расположения.
• Некоторые точки остаются плоскими из-за деструктивных помех – пучности.
• Точки с максимальным колебанием возникают из конструктивных помех – узлы.

Термины

• Поперечная волна – направление возмущения выступает перпендикулярным стороне перемещения.
• Деструктивные помехи – волны мешают друг другу, а точки не совпадают.
• Конструктивные помехи – волны мешают друг другу, но точки совпадают по фазам.

Пример

Вспомните о принципе функционирования гитары. При нажатии на струну, она начинает вибрировать. Это очень маленькая стоячая волна, чья частота остается практически постоянной. Частота характеризует высоту тона, так что звук – постоянная нота. Это основа для любого струнного инструмента.

Стоячей именуют кажущуюся неподвижную волну. То есть, она остается в стабильном положении. В струне это тип поперечной волны, где перемещение частичек среды выступает перпендикулярным направлению волнового распространения. Возникает, если две одинаковых волны, перемещающихся в разных направлениях, начинают друг другу мешать.

В случае со струнами возникает два сценария для волн: струна фиксируется на обоих концах или она фиксируется на одном и остается свободной на другом. Поперечная будет смещаться вдоль струны до тех пор, пока не достигнет второго конца. Потом она отражается и возвращается в исходное положение. Именно на этом этапе создаются помехи.

Волна отражается, но не инвертируется, как это делает поперечная волна с неподвижным концом

Поперечная волна отражается и инвертируется при сталкивании с фиксированным концом

Стоячие волны

В момент одного из этих сценариев падающая волна встречает отраженную. Они перемещаются в противоположные стороны, приводя к помехам. Если обладают одной частотой, то создают стоячую волну. Кажется, будто она лишена движений.

Если бы замедлили стоячую волну, то она приняла б такой вид. Она создана падающей волной на отраженной. Затем возвращается в том же направлении, в котором следовала ранее. Две волны сталкиваются и мешают друг другу

Конструктивные и деструктивные помехи

При встрече падающей и отраженной волн, амплитуда обоих достигает 0. По мере движения друг против друга, они создают два вида помех. Если полностью пребывают в фазе и контактируют конструктивно, то усиливаются, а при несоответствии фазе и деструктивном взаимодействии – уменьшаются. Так и формируется стоячая волна. Каждая точка среды со стоячей волной проходит сквозь колебания вверх и вниз, а амплитуда основывается на позициях этих точек. В итоге:

• Точки с максимальной высотой колебаний – пучности. Возникают при полной конструктивной помехе.
• Точки в стоячей воде, кажущиеся плоскими и неподвижными, – узлы. Относятся к деструктивным помехам.

Стоячие волны. 6.1 Стоячие волны в упругой среде

6.1 Стоячие волны в упругой среде

Согласно принципу суперпозиции, при распростране-нии в упругой среде одновременно нескольких волн воз-никает их наложение, причем волны не возмущают друг друга: колебания частиц среды являются векторной сум-мой колебаний, которые совершали бы частицы при рас-пространении каждой из волн в отдельности.

Волны, создающие колебания среды, разности фаз меж-ду которыми в каждой точке пространства постоянны, на-зываются когерентными.

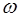
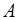
При сложении когерентных волн возникает явление интерференции, заключающееся в том, что в одних точ-ках пространства волны усиливают друг друга, а в других точках – ослабляют. Важный случай интерференции наб-людается при наложении двух встречных плоских волн с одинаковой частотой и амплитудой . Возникающие при этом колебания называют стоячей волной. Чаще все-го стоячие волны возникают при отражении бегущей вол-ны от преграды. При этом падающая волна и отраженная навстречу ей волна при сложении дают стоячую волну.

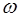
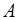
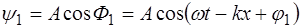
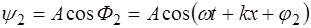
Получим уравнение стоячей волны. Возьмем две плос-кие гармонические волны, распространяющиеся навстечу друг другу вдоль оси X и имеющие одинаковую частоту и амплитуду :

,

,

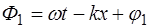
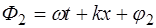
где – фаза колебаний точек среды при про-хождении первой волны;

– фаза колебаний точек среды при про-хождении второй волны.

Разность фаз в каждой точке на оси X не будет зави-сеть от времени, т.е. будет постоянной:

(6.2)

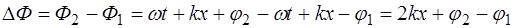
Следовательно, обе волны будут когерентными.

Возникшее в результате сложения рассматриваемых волн колебание частиц среды будет следующим:

. (6.3)

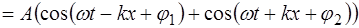
Преобразуем сумму косинусов углов по правилу (4.4) и получим:

(6.4)

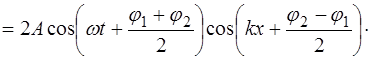
Перегруппировав множители, получим:

(6.5)

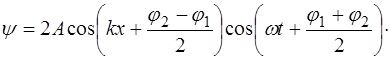
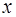
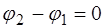
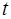
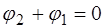
Для упрощения выражения выберем начало отсчета так, чтобы разность фаз и начало отсчета времени , чтобы и сумма фаз была равна нулю: .

Тогда уравнение для суммы волн примет вид:

. (6.6)

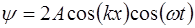
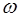
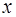
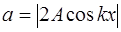
Уравнение (6.6) называется уравнением стоячей вол-ны. Из него видно, что частота стоячей волны равна частоте бегущей волны, а амплитуда, в отличие от бегу-щей волны, зависит от расстояния от начала отсчета :

. (6.7)

С учетом (6.7) уравнение стоячей волны принимает вид:

. (6.8)

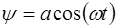
Таким образом, точки среды колеблются с частотой 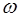, совпадающей с частотой бегущей волны, и амплитудой a, зависящей от положения точки на оси X. Соответственно, амплитуда изменяется по закону косинуса и имеет свои максимумы и минимумы (рис. 6.1).

Для того, чтобы наглядно представить расположение минимумов и максимумов амплитуды заменим, согласно (5.29), волновое число его значением:

. (6.9)

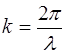
Тогда выражение (6.7) для амплитуды примет вид

(6.10)

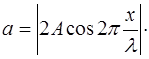
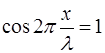
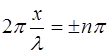
Отсюда становится видно, что амплитуда смещения мак-симальна при , т.е. в точках, координата кото-рых удовлетворяет условию:

, (6.11)

где

Отсюда получаем координаты точек, где амплитуда сме-щения максимальна:

; (6.12)

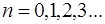
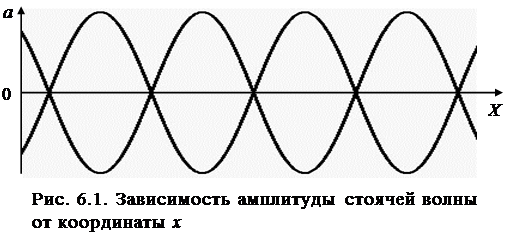
Точки, где амплитуда колебаний среды максимальна, называются пучностями волны.

Амплитуда волны равна нулю в точках, где 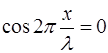. Координата таких точек, называемых узлами волны, удов-летворяет условию:

, (6.13)

где

Из (6.13) видно, что координаты узлов имеют зна-чения:

, (6.14)

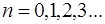
На рис. 6.2 показан примерный вид стоячей волны, от-мечено расположение узлов и пучностей. Видно, что со-седние узлы и пучности смещения отстоят друг от друга на одно и то же расстояние.

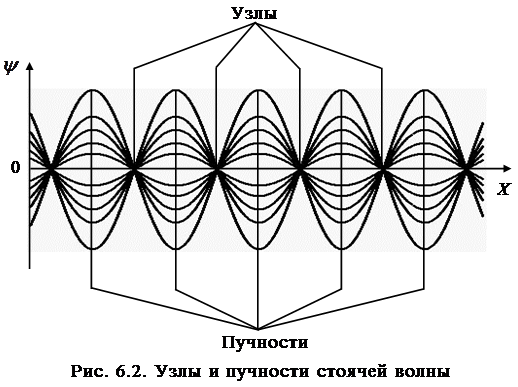Найдем расстояние между соседними пучностями и уз-лами. Из (6.12) получаем расстояние между пучностями:

(6.15)

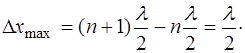
Расстояние между узлами получаем из (6.14):

(6.16)

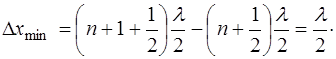
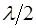
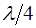
Из полученных соотношений (6.15) и (6.16) видно, что расстояние между соседними узлами, как и между сосед-ними пучностями, постоянно и равно ; узлы и пуч-ности сдвинуты относительно друг друга на (рис. 6.3).

Из определения длины волны можно записать выра-жение для длины стоячей волны: она равна половине дли-ны бегущей волны:

(6.17)

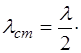
Запишем, с учетом (6.17), выражения для координат уз-лов и пучностей:

, (6.18)

, (6.19)

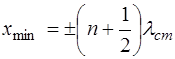
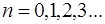
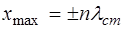
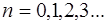
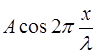
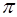
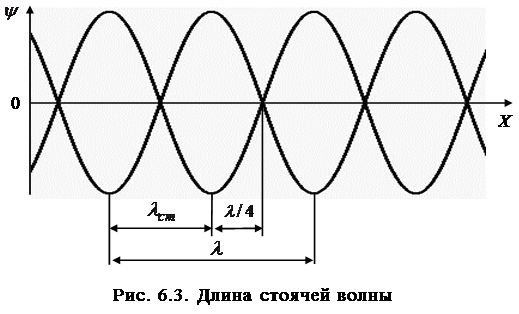Множитель , определяющий амплитуду стоя-чей волны, меняет свой знак при переходе через нулевое значение, вследствие чего фаза колебаний по разные сто-роны от узла отличается на . Следовательно, все точки, лежащие по разные стороны от узла, колеблются в про-тивофазе. Все точки, находящиеся между соседними уз-лами, колеблются синфазно.

Узлы условно разделяют среду на автономные области, в которых гармонические колебания совершаются незави-симо. Никакой передачи движения между областями нет, и, значит, перетекания энергии между областями нет. То есть нет передачи возмущения вдоль оси 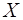. Поэтому волна называется стоячей.

Итак, стоячая волна образуется из двух противополож-но направленных бегущих волн равных частот и амп-литуд. Векторы Умова каждой из этих волн равны по мо-дулю и противоположны при направлению, и при сложе-нии дают ноль. Следовательно, стоячая волна энергии не переносит.

6.2 Примеры стоячих волн

6.2.1 Стоячая волна в струне

Расмотрим струну длиной L, закрепленную с обоих кон-цов (рис. 6.4).

Расположим вдоль струны ось X таким образом, чтобы левый конец струны имел координату x=0, а правый – x=L. В струне возникают колебания, описываемые урав-нением:

(6.20)

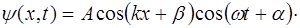
Запишем граничные условия для рассматриваемой стру-ны. Поскольку её концы закреплены, то в точках с коор-динатами x=0 и x=L колебаний нет:

(6.21)

(6.22)

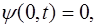
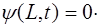
Найдем уравнение колебаний струны исходя из запи-санных граничных условий. Запишем уравнение (6.20) для левого конца струны с учетом (6.21):

(6.23)

Соотношение (6.23) выполняется для любого времени t в двух случаях:

1. . Это возможно в том случае, если коле-бания в струне отсутствуют ( ). Данный случай инте-реса не представляет, и мы его рассматривать не будем.

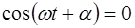
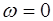
2. . Здесь фаза . Этот случай и позволит нам получить уравнение колебаний струны.

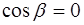
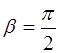
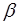
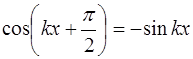
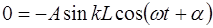
Подставим полученное значение фазы в граничное условие (6.22) для правого конца струны:

. (6.25)

, (6.26)

. (6.27)

Снова возникают два случая, при которых выполняется соотношение (6.27). Случай, когда колебания в струне от-сутствуют ( 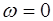), мы рассматривать не будем.

Во втором случае должно выполняться равенство:

, (6.27)

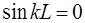
а это возможно, только когда аргумент синуса кратен це-лому числу :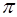

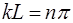
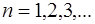
, (6.28)

Значение мы отбрасываем, т.к. при этом , а это означало бы или нулевую длину струны (L=0) или вол-новое число k=0. Учитывая связь (6.9) между волновым числом и длиной волны видно, что для того, чтобы вол-новое число равнялось бы нулю, длина волны должна бы быть бесконечной, а это означало бы отсутствие колебаний.

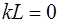
Из (6.28) видно, что волновое число при колебаниях струны, закрепленной с обоих концов, может принимать только определенные дискретные значения:

(6.30)

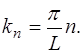
Учитывая (6.9), запишем (6.30) в виде:

(6.31)

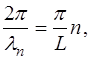
откуда волучаем выражение для возможных длин волн в струне:

(6.31)

Другими словами, на длине струны L должно уклады-ваться целое число n полуволн:

(6.32)

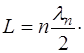
Соответствующие частоты колебаний можно опреде-лить из (5.7):

. (6.33)

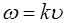
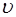
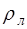
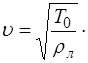
Здесь – фазовая скорость волны, зависящая, соглас-но (5.102), от линейной плотности струны и силы на-тяжения струны :

(6.34)

Подставив (6.34) в (6.33), получим выражение, описы-вающее возможные частоты колебаний струны:

, (6.36)

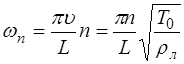
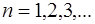
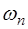
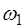
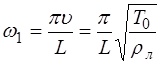
Частоты называют собственными частотами стру-ны. Частоту (при n = 1):

(6.37)

называют основной частотой (или основным тоном) струны. Частоты, определяемые при n>1 называются обертонами или гармониками. Номер гармоники равен n-1. Например, частота :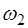

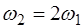
(6.38)

соответствует первой гармонике, а частота :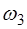

(6.39)

сответствует второй гармонике, и т.д. Поскольку струну можно представить в виде дискретной системы с беско-нечным числом степеней свободы, то каждая гармоника является модой колебаний струны. В общем случае коле-бания струны представляют собой суперпозицию мод.

Каждой гармонике соответствует своя длина волны. Для основного тона (при n=1) длина волны:

, (6.40)

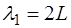
соответственно для первой и второй гармоники (при n=2 и n=3) длины волн будут:

, (6.41)

(6.42)

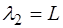
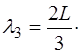
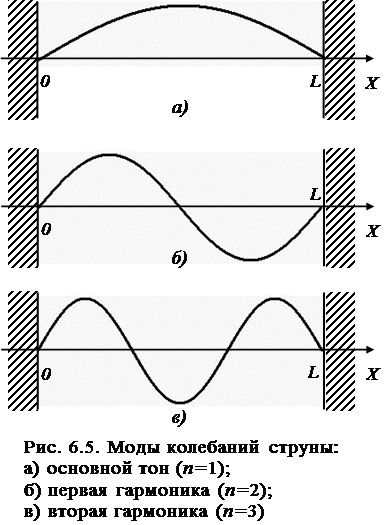
На рис.6.5 показан вид нескольких мод колебаний, осуществляемых струной.

Таким образом, струна с закрепленными концами реа-лизует в рамках классической физики исключительный случай – дискретный спектр частоты колебаний (или длин волн). Таким же образом ведет себя упругий стер-жень с одним или обоими зажатыми концами и колебания воздушного столба в трубах, что и будет рассмотрено в последующих разделах.

6.2.2 Влияние начальных условий на движение

непрерывной струны. Фурье-анализ

Колебания струны с зажатыми концами помимо дис-кретного спектра частот колебаний обладают еще одним важным свойством: конкретная форма колебаний струны зависит от способа возбуждения колебаний, т.е. от на-чальных условий. Рассмотрим подробней.

Уравнение (6.20), описывающее одну моду стоячей вол-ны в струне, является частным решением дифференциаль-ного волнового уравнения (5.61). Поскольку колебание стру-ны складывается из всех возможных мод (для струны – бес-конечное количество), то и общее решение волнового уравнения (5.61) складывается из бесконечного числа частных решений:

, (6.43)

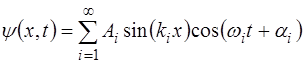
где i – номер моды колебаний. Выражение (6.43) записа-но с учетом того, что концы струны закреплены:

, (6.44)

, (6.45)

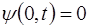
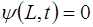
а также с учетом связи частоты i-й моды и ее волнового числа:

(6.46)

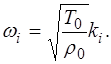
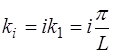
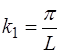
Здесь – волновое число i-й моды;

– волновое число 1-й моды;

Найдем величину начальной фазы для каждой моды колебаний. Для этого в момент времени t=0 придадим струне форму, описываемую функцией f₀(x), выражение для которой получим из (6.43):

. (6.47)

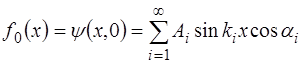
На рис. 6.6 показан пример формы струны, описывае-мой функцией f₀(x).

В момент времени t=0 струна еще покоится, т.е. ско-рость всех ее точек равна нулю. Из (6.43) найдем выраже-ние для скорости точек струны:

, (6.48)

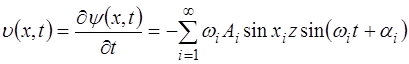
и, подставив в него t=0, получим выражение для скорос-ти точек струны в начальный момент времени:

. (6.49)

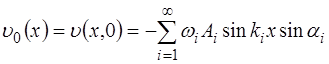
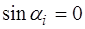
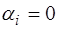
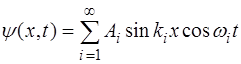
Поскольку в начальный момент времени скорость рав-на нулю, то выражение (6.49) будет равно нулю для всех точек струны, если . Из этого следует, что на-чальная фаза для всех мод тоже равна нулю ( ). С учетом этого выражение (6.43), описывающее движение струны, принимает вид:

, (6.50)

а выражение (6.47), описывающее начальную форму стру-ны, выглядит как:

. (6.51)

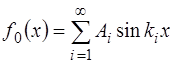
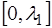
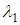
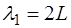
Стоячая волна в струне описывается функцией, перио-дичной на интервале , где равна двум длинам струны (рис. 6.7):

. (6.52)

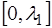
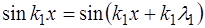
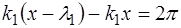
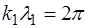
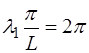
Это видно из того, что периодичность на интервале означает:

. (6.53)

; (6.54)

; (6.55)

, (6.56)

что и приводит нас к выражению (6.52).

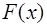
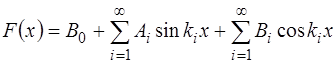
Из математического анализа известно, что любая пе-риодическая функция может быть разложена с высо-кой точностью в ряд Фурье:

, (6.57)

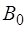
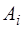
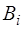
где , , – коэффициенты Фурье.

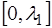
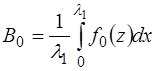
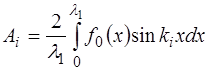
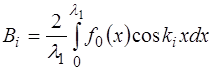
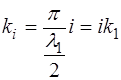
В нашем случае, когда функция является периодичес-кой на интервале , коэффициенты Фурье, согласно [1], рассчитываются как:

, (6.58)

, (6.59)

, (6.60)

. (6.61)

В математике в курсе Фурье-анализа показано, что по-лученные таким образом коэффициенты Фурье для разло-жения периодической функции 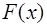фактически и явля-ются коэффициентами разложения функции f₀(x).

Фурье-анализ позволяет разложить колебание, совер-шаемое струной в спектр, т.е. выяснить, какие моды ко-лебаний действительно имеют место при данном способе возбуждения струны.

Рассмотрим два способа возбуждения колебаний струны.

Способ 1. Струне в начальный момент времени прида-ется форма, соответствующая первой моде колебаний и описываемая функцией:

. (6.62)

После того, как струна отпускается, она начинает со-вершать колебания из начального положения. Расчеты по-казывают, что коэффициенты Фурье для этого случая все равны нулю, кроме одного, который равен амплитуде A:

. (6.63)

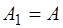
При таком способе возбуждения возникает только одна мода колебаний; никаких обертонов нет.

Способ 2. Струна отводится от положения равновесия посередине, как это происходит в струнных инстру-ментах. Вид начальной формы представлен на рис. 6.8.

Форма струны, изображенная на рис. 6.8, описывается функцией:

при ,

при .

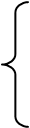
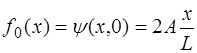
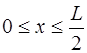
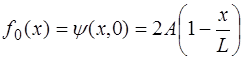
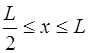
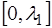
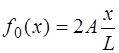
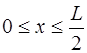
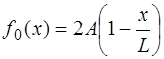
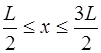
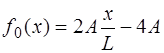
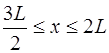
Функция, соответствующая (6.64), и которая является пе-риодической на интервале , записывается следую-щим образом:

при ,

при , (6.65)

при .

Вид периодической функции (6.65) показан на рис.6.9:

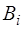
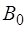
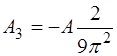
Расчеты показывают, что все коэффициенты Фурье для такой функции равны нулю (включая и коэффициент ). Первые три коэффициента A₁, A₂, A₃ соответственно равны:

, (6.66)

, (6.67)

. (6.68)

Как уже отмечалось, полученные таким образом коэф-фициенты Фурье для разложения периодической функ-ции 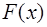фактически и являются коэффициентами разло-жения функции f₀(x).

Тогда, с учетом трех первых слагаемых ряда Фурье, функция (6.64) может быть приближенно представлена следующим образом:

(6.69)

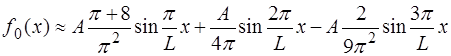
Мы нашли только три первых члена Фурье-разложения функции (6.64). Конечно, полученный нами ряд Фурье (6.69) при конечном количестве членов, в нашем случае равном трём, может воспроизвести исходную функцию лишь при-ближённо. Однако, вычисления коэффициентов Фурье могут быть продолжены. Получится, что при рассматриваемом на-ми случае колебаний в струне возникает много гармоник (теоретически, бесконечный ряд гармоник).

Сравнивая первый и второй рассмотренные случаи, мы видим, что в первом из них была только одна мода, а во втором возникает много гармоник.

Таким образом, рассмотренные случаи показывают, что конкретная форма колебаний струны, зажатой с двух сторон, существенно зависит от способа возбуждения ко-лебаний, т.е., от начальных условий.

Дата добавления: 2015-06-12 ; просмотров: 4184 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ