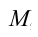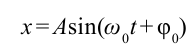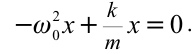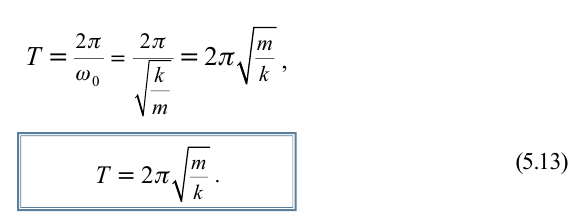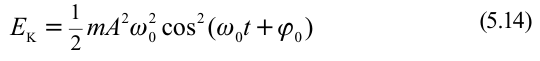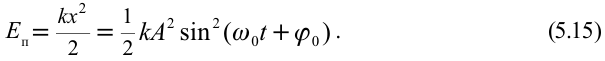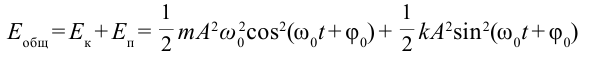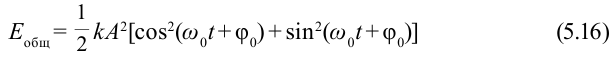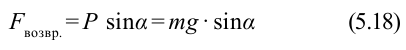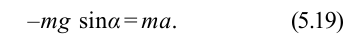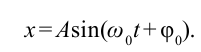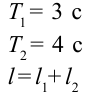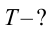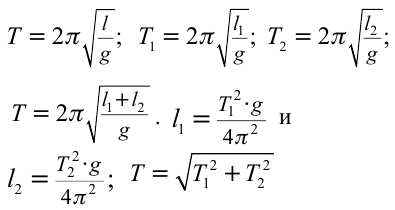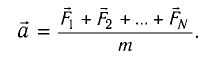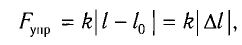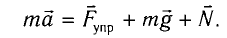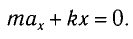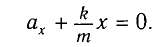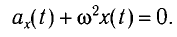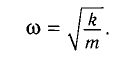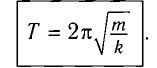Уравнение свободных колебаний математического маятника имеет следующий

Формулы математического маятника

Определение и формулы математического маятника

Математический маятник — это колебательная система, являющаяся частным случаем физического маятника, вся масса которого сосредоточена в одной точке, центре масс маятника.

Обычно математический маятник представляют как шарик, подвешенный на длинной невесомой и нерастяжимой нити. Это идеализированная система, совершающая гармонические колебания под действием силы тяжести. Хорошим приближением к математическому маятнику массивный маленький шарик, осуществляющий колебания на тонкой длинной нити.

Галилей первым изучал свойства математического маятника, рассматривая качание паникадила на длинной цепи. Он получил, что период колебаний математического маятника не зависит от амплитуды. Если при запуске мятника отклонять его на разные малые углы, то его колебания будут происходить с одним периодом, но разными амплитудами. Это свойство получило название изохронизма.

Уравнение движения математического маятника

Математический маятник — классический пример гармонического осциллятора. Он совершает гармонические колебания, которые описываются дифференциальным уравнением:

где $\varphi $ — угол отклонения нити (подвеса) от положения равновесия.

Решением уравнения (1) является функция $\varphi (t):$

где $\alpha $ — начальная фаза колебаний; $<\varphi >_0$ — амплитуда колебаний; $<\omega >_0$ — циклическая частота.

Колебания гармонического осциллятора — это важный пример периодического движения. Осциллятор служит моделью во многих задачах классической и квантовой механики.

Циклическая частота и период колебаний математического маятника

Циклическая частота математического маятника зависит только от длины его подвеса:

Период колебаний математического маятника ($T$) в этом случае равен:

Выражение (4) показывает, что период математического маятника зависит только от длины его подвеса (расстояния от точки подвеса до центра тяжести груза) и ускорения свободного падения.

Уравнение энергии для математического маятника

При рассмотрении колебаний механических систем с одной степенью свободы часто берут в качестве исходного не уравнения движения Ньютона, а уравнение энергии. Так как его проще составлять, и оно является уравнением первого порядка по времени. Предположим, что трение в системе отсутствует. Закон сохранения энергии для совершающего свободные колебания математического маятника (колебания малые) запишем как:

где $E_k$ — кинетическая энергия маятника; $E_p$ — потенциальная энергия маятника; $v$ — скорость движения маятника; $x$ — линейное смещение груза маятника от положения равновесия по дуге окружности радиуса $l$, при этом угол — смещение связан с $x$ как:

Максимальное значение потенциальной энергии математического маятника равно:

Максимальная величина кинетической энергии:

где $h_m$ — максимальная высота подъема маятника; $x_m$- максимальное отклонение маятника от положения равновесия; $v_m=<\omega >_0x_m$ — максимальная скорость.

Примеры задач с решением

Задание. Какова максимальная высота подъема шарика математического маятника, если его скорость движения при прохождении положения равновесия составляла $v$?

Решение. Сделаем рисунок.

Пусть ноль потенциальной энергии шарика в его положении равновесия (точка 0).В этой точке скорость шарика максимальна и равна по условию задачи $v$. В точке максимального подъема шарика над положением равновесия (точка A), скорость шарика равна нулю, потенциальная энергия максимальна. Запишем закон сохранения энергии для рассмотренных двух положений шарика:

Из уравнения (1.1) найдем искомую высоту:

Ответ. $h=\frac<2g>$

Задание. Каково ускорение силы тяжести, если математический маятник имеющий длину $l=1\ м$, совершает колебания с периодом равным $T=2\ с$? Считайте колебания математического маятника малыми.\textit<>

Решение. За основу решения задачи примем формулу для вычисления периода малых колебаний:

Выразим из нее ускорение:

Проведем вычисления ускорения силы тяжести:

Ответ. $g=9,87\ \frac<м><с^2>$

Пружинные и математические маятники в физике — виды, формулы и определения с примерами

Содержание:

Пружинные и математические маятники:

Тело или система тел, совершающие периодические колебательные движения, называются маятниками. Большинство колебательных движений, встречающихся в природе, напоминают движение пружинных и математических маятников.

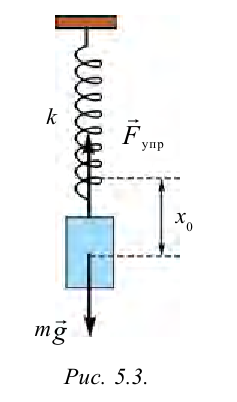
Система, состоящая из груза массой

Если немножко растянуть пружину и отпустить, то груз придет в колебательное движение в вертикальном направлении.
С помощью опытов мы определили, что смещение груза в зависимости от времени изменяется следующbм образом:

Если учесть, что ускорение тела, совершающего гармонические колебания 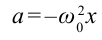, то уравнение (5.10) примет вид:

Из этого уравнения мы имеем:

Значит, частота циклического колебания тела, совершающего гармоническое колебание, зависит от параметров тел, входящих в систему колебания. Формула (5.12) называется формулой для
определения циклической (периодической) частоты пружинного маятника.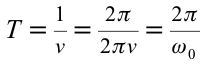

Период колебания пружинного маятника прямо пропорционален выведенному из-под квадратного корня значению массы груза и обратно пропорционален выведенному из-под квадратного корня значению упругости пружины.
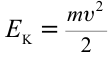
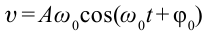
Рассмотрим обмен энергиями в пружинном маятнике. Кинетическая энергия маятника, если не учитывать массу пружины, равна кинетической энергии груза, . В предыдущих темах было показано, что скорость можно выразить формулой . В таком случае кинетическая энергия маятника равна

Потенциальная энергия пружинного маятника равна энергии деформации пружины, т.е.:

В большинстве случаев важно знать полную энергию системы:

Если учесть, что ,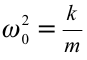

Обратите внимание, что полная энергия пружинного маятника является постоянной величиной, не зависящей от времени, т.е. соблюдается выполнение закона сохранения механической энергии.
Материальная точка, подвешенная на нерастяжимой и невесомой нити и совершающая периодическое колебательное движение вокруг равновесного состояния, называется математическим маятником.

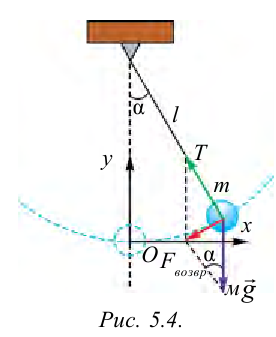
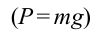
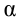
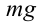
Когда маятник находится в устойчивом равновесном состоянии, вес материальной точки уравновешивает силу натяжения (рис. 5.4), так как их модули равны и направлены по одной линии в противоположные стороны. Если наклонить маятник на угол , силы и не смогут уравновесить друг друга из-за взаимного расположения под углом. В результате сложения таких сил появится возвращающая сила, которая вернет маятник в равновесное состояние. Если отпустить маятник, то под воздействием возвращающей силы он начинает двигаться в сторону равновесного состояния.

Из рис. 5.4. видим, что:

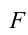
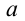
Согласно второму закону Ньютона, сила придает материальной точке ускорение , поэтому

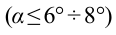
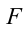
Из-за того, что угол наклона очень маленький , а сила направлена противоположно смещению, формулу (5.19) можно записать в виде

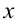
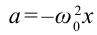
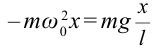
Если смещение материальной точки (шарика) во время колебательного процесса отметить буквой и учитывать соотношение , получим
Следовательно
Исходя из смысла периода колебания и учитывая, что 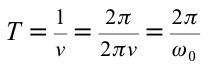получаем

Эта формула, определяющая период колебания математического маятника, называется формулой Гюйгенса. Отсюда вытекают следующие законы математического маятника:

1. при маленьких углах наклона (а) математического маятника, его период колебания не зависит от амплитуды колебания.
2. период колебания математического маятника также не зависит от массы подвешенного на него груза;
3. период колебания математического маятника прямо пропорционален выведенному из-под квадратного корня значению длины маятника и обратно пропорционален выведенному из-под квадратного корня значению ускорения свободного падения.

Отсюда колебание математического маятника записывается следующим выражением:

Следует отметить, что когда амплитуда колебания или угол наклона велики, колебания математического маятника не являются гармоническим. В этом случае нельзя считать 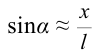и для решения уравнения движения не применяется закон синусов или косинусов.

Пример:

Период колебания первого маятника равен 3 сек, второго – 4 сек. Найдите период колебания маятника с длиной, равной сумме длин этих маятников.

Решение: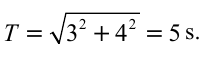

Ответ: 5 cек.

Пружинный и математический маятники

Второй закон Ньютона (основной закон динамики): ускорение, приобретаемое материальной точкой, прямо пропорционально равнодействующей всех сил, действующих на нее, и обратно пропорционально массе материальной точки:

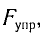
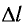
Закон Гука: модуль силы упругости , возникающей в теле при упругих деформациях, прямо пропорционален его абсолютному удлинению (сжатию) :

где k — жесткость тела, 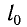— длина недеформированного тела, l — длина деформированного тела.

Рассмотрим пружинный маятник, представляющий собой колебательную систему, образованную грузом на пружине.

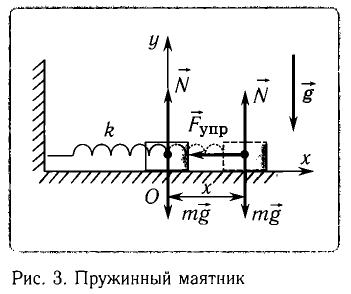
Пусть груз массой т, лежащий на гладкой горизонтальной поверхности, прикреплен к свободному концу невесомой пружины жесткостью k (рис. 3). Второй конец пружины закреплен относительно данной инерциальной системы отсчета (ИСО).

Выведем груз из положения равновесия, сместив его на расстояние х вправо. В пружине возникнет сила упругости 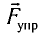направленная влево.

Запишем второй закон Ньютона для движения груза:

В проекции на ось Ох действующих на груз сил с учетом закона Гука получаем

или

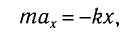
Это уравнение аналогично уравнению гармонических колебаний

Сравнивая эти два уравнения, находим циклическую частоту колебаний пружинного маятника:

Тогда период колебаний пружинного маятника можно найти по формуле

Как следует из полученной формулы, период колебаний пружинного маятника не зависит от амплитуды его колебаний (в пределах выполнимости закона Гука).

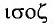
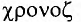
Свойство независимости периода колебаний маятника от амплитуды называется изохронностью (от греческих слов , — равный и — время). Таким образом, колебания пружинного маятника обладают свойством изохронности.

Изохронность колебаний маятника была открыта Галилео Галилеем в 1583 г. при изучении движения грузика, подвешенного на нити. Моделью данной колебательной системы является математический маятник.

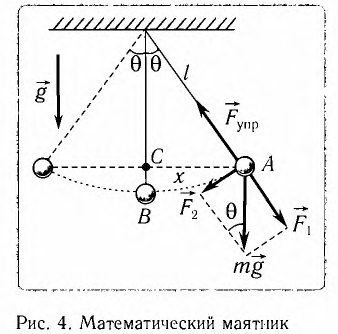
Математическим маятником называется материальная точка массой т, подвешенная на невесомой нерастяжимой нити длиной l в поле каких-либо сил, например силы тяжести Земли (рис. 4).

Математический маятник — это идеализированная модель реального маятника при условии, что длина нити намного больше размеров подвешенного на ней тела и масса нити намного меньше массы тела. Кроме того, деформацией нити можно пренебречь.

Галилео Галилей экспериментально определил, что период малых колебаний (9

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Свободные колебания. Математический маятник

При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.

Когда тело принимает положение равновесия при движении, это говорит о наличии минимальной его скорости. Тогда кинетическая энергия обладает максимальным значением, а потенциальная – минимальным. По 3 -му закону Ньютона формула силы натяжения записывается как T = m g при вертикальном подвешивании тела на нити. Уменьшение потенциальной приводит к увеличению кинетической. Дальнейшее движение показывает, что происходит уменьшение кинетической и увеличение потенциальной.

Гармонические колебания – это пример превращения кинетической энергии в потенциальную и наоборот.

Рисунок 2 . 4 . 1 . Модель превращения энергии при колебаниях.

Математический и пружинный маятник

Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.

Формулы, характеризующие груз на пружине:

E = E k + E p = m υ 2 2 + k x 2 2 , ω 0 2 = k m , ( E p ) m a x = k x m 2 2 , ( E k ) m a x = m υ m 2 2 = m ω 0 2 x m 2 2 = ( E p ) m a x .

Выражения при малых колебаниях математического маятника записываются:

E = E k + E p = m υ 2 2 + m g h = m υ 2 2 + m g x 2 2 l , ω 0 2 = g l , ( E p ) m a x = m g h m = m g x m 2 2 l , ( E k ) m a x = m υ m 2 2 = m ω 0 2 x m 2 2 = ( E p ) m a x .

Значение h m является максимальной высотой подъема маятника, x m и υ m = ω 0 x m – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.

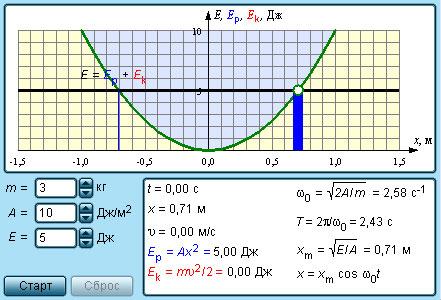
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.

Если рассматривать колебания с грузом массой m на пружине с жесткостью k , тогда смещение груза x ( t ) из положения равновесия и его скорость υ ( t ) могут изменяться со временем согласно законам:

x ( t ) = x m cos ( ω 0 t ) , где ω 0 2 = k m ,

υ ( t ) = — ω x m sin ( ω 0 t ) .

Формулы кинетической и потенциальной энергии запишутся так:

E p ( t ) = 1 2 k x 2 = 1 2 k x m 2 cos 2 ω 0 t = 1 4 k x m 2 ( 1 + cos 2 ω 0 t ) ,

E k ( t ) = 1 2 m υ 2 = 1 2 k ω 0 2 x m 2 sin 2 ω 0 t = 1 4 k x m 2 ( 1 — cos 2 ω 0 t ) .

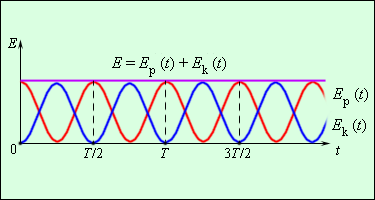
Рисунок 2 . 4 . 2 показывает два графика функций изменения E p ( t ) и E k ( t ) . Обе энергии в период колебаний T = 2 π ω 0 , достигают максимальных значений по два раза. Значение их суммы не изменяется E p ( t ) + E k ( t ) = E = c o n s t .

Рисунок 2 . 4 . 2 . Превращения энергии при свободных колебаниях.

Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).

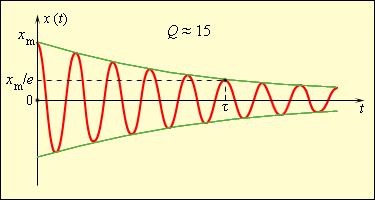
При переходе части механической энергии во внутреннюю энергию теплового движения атомов и молекул колебания становятся затухающими, как показано на рисунке 2 . 4 . 3 .

Рисунок 2 . 4 . 3 . Свободные затухающие механические колебания.

Скорость затухания колебаний зависит от величины сил трения.

Частота. Добротность. Формулы

Промежуток времени τ с уменьшением колебаний в e ≈ 2 , 7 раз называют временем затухания.

Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.

Колебательная система с затухающими колебаниями характеризуется добротностью Q .

Определение параметра представляет собой произведение числа полных колебаний N за время затухания τ на значение π :

Повышение Q колебательной системы происходит при медленных затуханиях свободных колебаний. На рисунке 2 . 4 . 3 показано, что Q имеет значение, приближенное к 15 .

Добротность механических колебательных систем может достигать огромных значений. Для определения Q колебательной системы применяют формулу:

Q = 2 π З а п а с э н е р г и и в к о л е б а т е л ь н о й с и с т е м е П о т е р я э н е р г и и з а 1 п е р и о д к о л е б а н и й .

То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.