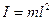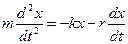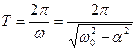Уравнение свободных незатухающих колебаний математического маятника

Математический маятник

Математическим маятником называется идеализированная система, состоящая из материальной точки массой m, подвешенной на нерастяжимой невесомой нити, которая колеблется под действием силы тяжести.

Момент инерции материальной точки относительно оси вращения проходящей через точку подвеса равен

Математический маятник является частным случаем физического маятника, поэтому, период колебаний математического маятника можно вычислить по формуле (5.24), учитывая, что приведенная длина физического маятника и длина математического маятника равны (L = l)

.

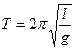
Затухание колебания

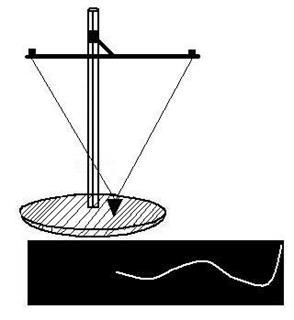
Движение в реальных системах всегда сопровождается трением и в результате потери энергии колебания затухают. Свободные колебания всегда являются затухающими. Затухающие колебания можно продемонстрировать с помощью установки изображенной на рис.5.6. Если привести в колебание воронку с песком, то при ее движении всыпающийся песок оставляет след затухающих колебаний.

Рис.5.6

При малых скоростях колебания сила трения пропорциональна скорости

(5.25)

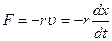
где r – коэффициент сопротивления.

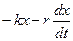
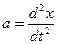
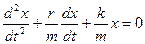
На колеблющуюся систему массой m действует сумма сил ( ), которая вызывает ускорение этой системы, т.е.

(5.26)

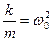
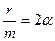
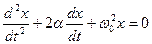
Зная, что и, обозначив (α – коэффициент затухания), получим дифференциальное уравнение затухающих колебаний

(5.27)

Решением этого уравнения при условии ω₀ > α является выражение

(5.28)

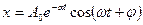
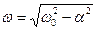
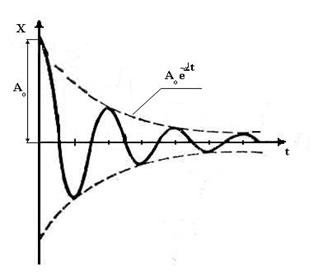
Здесь – частота затухающих колебаний, а постоянные А₀ и φ зависят от начальных условий.

На рис.5.7. представлен график функции (5.28). На графике пунктиром показаны кривые затухания амплитуд. Уменьшение амплитуд происходит по закону

(5.29)

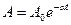
где α – коэффициент затухания, характеризующий скорость затухания колебаний.

Рис.5.7

Найдем время τ, в течение которого амплитуда уменьшается в е раз. Если в формулу (5.29) подставить 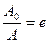, получим

at = 1 или .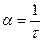

Следовательно, коэффициент затухания обратно пропорционален времени, за которое амплитуда уменьшается в е раз.

Мерой затухания является величина называемая логарифмическим декрементом затухания δ. Логарифмический декремент затухания есть логарифм отношения двух последовательных амплитуд колебаний отличающихся на период.

(5.30)

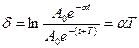
При малых значениях δ пользуются понятием добротности .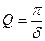

Период затухающих колебаний равен

При 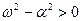система совершает периодические затухающие колебания, как показано на рис.5.8.

Когда 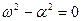, то Τ ® ∞. Это значит, что движение перестает быть периодическим (см. рис.5.8). В зависимости от начальных условий система возвращается в положение равновесия по одной из двух указанных кривых.

Дата добавления: 2015-10-26 ; просмотров: 5074 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ

Свободные колебания. Математический маятник

При наличии механических колебаний происходит периодическое изменение кинетической и потенциальной энергии. Обращение в ноль кинетической энергии и скорости связано с максимальным отклонением тела от положения равновесия. Энергия такого колеблющегося тела достигает максимального значения. Если груз располагается на горизонтальной пружине, то потенциальная энергия считается энергией упругих деформаций пружины. У математического маятника – это энергия в поле тяготения Земли.

Когда тело принимает положение равновесия при движении, это говорит о наличии минимальной его скорости. Тогда кинетическая энергия обладает максимальным значением, а потенциальная – минимальным. По 3 -му закону Ньютона формула силы натяжения записывается как T = m g при вертикальном подвешивании тела на нити. Уменьшение потенциальной приводит к увеличению кинетической. Дальнейшее движение показывает, что происходит уменьшение кинетической и увеличение потенциальной.

Гармонические колебания – это пример превращения кинетической энергии в потенциальную и наоборот.

Рисунок 2 . 4 . 1 . Модель превращения энергии при колебаниях.

Математический и пружинный маятник

Когда колебательная система не имеет силы трения, тогда остается неизменной полная механическая энергия.

Формулы, характеризующие груз на пружине:

E = E k + E p = m υ 2 2 + k x 2 2 , ω 0 2 = k m , ( E p ) m a x = k x m 2 2 , ( E k ) m a x = m υ m 2 2 = m ω 0 2 x m 2 2 = ( E p ) m a x .

Выражения при малых колебаниях математического маятника записываются:

E = E k + E p = m υ 2 2 + m g h = m υ 2 2 + m g x 2 2 l , ω 0 2 = g l , ( E p ) m a x = m g h m = m g x m 2 2 l , ( E k ) m a x = m υ m 2 2 = m ω 0 2 x m 2 2 = ( E p ) m a x .

Значение h m является максимальной высотой подъема маятника, x m и υ m = ω 0 x m – максимальными значениями отклонения физического маятника от положения равновесия и его скорости.

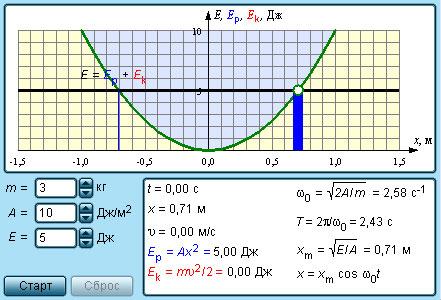
Для объяснения превращения энергии при свободных механических колебаниях без силы трения приводится иллюстрация.

Если рассматривать колебания с грузом массой m на пружине с жесткостью k , тогда смещение груза x ( t ) из положения равновесия и его скорость υ ( t ) могут изменяться со временем согласно законам:

x ( t ) = x m cos ( ω 0 t ) , где ω 0 2 = k m ,

υ ( t ) = — ω x m sin ( ω 0 t ) .

Формулы кинетической и потенциальной энергии запишутся так:

E p ( t ) = 1 2 k x 2 = 1 2 k x m 2 cos 2 ω 0 t = 1 4 k x m 2 ( 1 + cos 2 ω 0 t ) ,

E k ( t ) = 1 2 m υ 2 = 1 2 k ω 0 2 x m 2 sin 2 ω 0 t = 1 4 k x m 2 ( 1 — cos 2 ω 0 t ) .

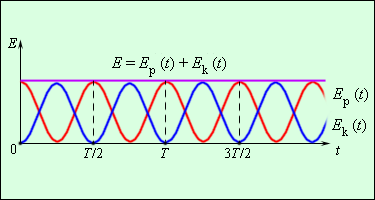
Рисунок 2 . 4 . 2 показывает два графика функций изменения E p ( t ) и E k ( t ) . Обе энергии в период колебаний T = 2 π ω 0 , достигают максимальных значений по два раза. Значение их суммы не изменяется E p ( t ) + E k ( t ) = E = c o n s t .

Рисунок 2 . 4 . 2 . Превращения энергии при свободных колебаниях.

Реальные условия для колебательной системы – это наличие воздействия сил трения (сопротивления).

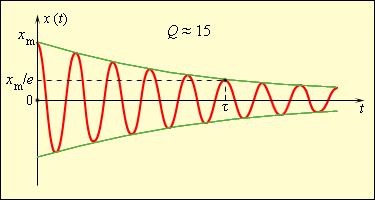
При переходе части механической энергии во внутреннюю энергию теплового движения атомов и молекул колебания становятся затухающими, как показано на рисунке 2 . 4 . 3 .

Рисунок 2 . 4 . 3 . Свободные затухающие механические колебания.

Скорость затухания колебаний зависит от величины сил трения.

Частота. Добротность. Формулы

Промежуток времени τ с уменьшением колебаний в e ≈ 2 , 7 раз называют временем затухания.

Скорость затухания зависит от частоты свободных колебаний, как видно из формулы. При увеличении действия сил трения происходит уменьшение собственной частоты. Если действия силы трения достаточно велико, то изменение частоты становятся заметными.

Колебательная система с затухающими колебаниями характеризуется добротностью Q .

Определение параметра представляет собой произведение числа полных колебаний N за время затухания τ на значение π :

Повышение Q колебательной системы происходит при медленных затуханиях свободных колебаний. На рисунке 2 . 4 . 3 показано, что Q имеет значение, приближенное к 15 .

Добротность механических колебательных систем может достигать огромных значений. Для определения Q колебательной системы применяют формулу:

Q = 2 π З а п а с э н е р г и и в к о л е б а т е л ь н о й с и с т е м е П о т е р я э н е р г и и з а 1 п е р и о д к о л е б а н и й .

То есть добротность способна характеризовать относительную убыль (затухание) энергии при наличии действия силы трения на данном промежутке времени, равняющемуся одному периоду колебаний.

Гармонические колебания

О чем эта статья:

9 класс, 11 класс, ЕГЭ/ОГЭ

Механические колебания

Механические колебания — это физические процессы, которые точно или приблизительно повторяются через одинаковые интервалы времени.

Колебания делятся на два вида: свободные и вынужденные.

Свободные колебания

Это колебания, которые происходят под действием внутренних сил в колебательной системе.

Они всегда затухающие, потому что весь запас энергии, сообщенный в начале, в конце уходит на совершение работы по преодолению сил трения и сопротивления среды (в этом случае механическая энергия переходит во внутреннюю). Из-за этого свободные колебания почти не имеют практического применения.

Вынужденные колебания

А вот вынужденные колебания восполняют запас энергии внешним воздействием. Если это происходит каждый период, то колебания вообще затухать не будут.

Вынужденные колебания — это колебания, которые происходят под действием внешней периодически меняющейся силы.

Частота, с которой эта сила воздействует, равна частоте, с которой система будет колебаться.

Например, качели. Если вас кто-то будет на них качать, каждый раз давая толчок, когда вы приходите в одну и ту же точку — такое колебание будет считаться вынужденным.

Это колебание все еще будет считаться вынужденным, если вас будут раскачивать из положения равновесия. Просто в данном случае амплитуда (о которой речь пойдет чуть ниже) будет увеличиваться с каждым колебанием.

Автоколебания

Иногда вынужденному колебанию не нужно внешнего воздействия, чтобы случиться. Бывают такие системы, в которых это внешние воздействие возникает само из-за способности регулировать поступление энергии от постоянного источника.

У автоколебательной системы есть три важных составляющих:

• сама колебательная система
• источник энергии
• устройство обратной связи, обеспечивающей связь между источником и системой

Часы с кукушкой — пример автоколебательной системы. Гиря на ниточке (цепочке) стремится вращать зубчатое колесо (храповик). При колебаниях маятника анкер цепляет за зубец, и вращение приостанавливается.

Но в результате маятник получает толчок, компенсирующий потери энергии из-за трения. Потенциальная энергия гири, которая постепенно опускается, расходуется на поддержание незатухающих колебаний.

Характеристики колебаний

Чтобы перейти к гармоническим колебаниям, нам нужно описать величины, которые помогут нам эти колебания охарактеризовать. Любое колебательное движение можно описать величинами: период, частота, амплитуда, фаза колебаний.

Период — это время одного полного колебания. Измеряется в секундах и обозначается буквой T.

Формула периода колебаний

T = t/N

N — количество колебаний [—]

Также есть величина, обратная периоду — частота. Она показывает, сколько колебаний совершает система в единицу времени.

Формула частоты

ν = N/t = 1/T

N — количество колебаний [—]

Амплитуда — это максимальное отклонение от положения равновесия. Измеряется в метрах и обозначается либо буквой A, либо x max .

Она используется в уравнении гармонических колебаний:

Гармонические колебания

Простейший вид колебательного процесса — простые гармонические колебания, которые описывают уравнением:

Уравнение гармонических колебаний

x — координата в момент времени t [м]

t — момент времени [с]

(2πνt) в этом уравнении — это фаза. Ее обозначают греческой буквой φ

Фаза колебаний

t — момент времени [с]

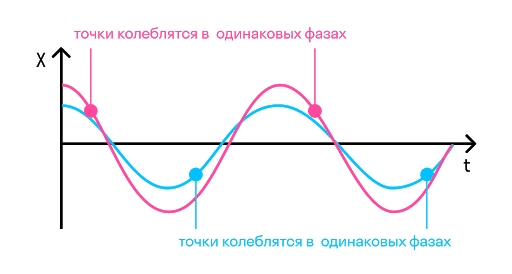
Фаза колебаний — это физическая величина, которая показывает отклонение точки от положения равновесия. Посмотрите на рисунок, на нем изображены одинаковые фазы:

Например, в тех же самых часах с кукушкой маятник совершает колебания. Он качается слева направо и приходит в самую правую точку. В той же фазе он будет находиться, когда придет в ту же точку, идя справа налево. Если мы возьмем точку на сантиметр левее самой правой, то идя в нее не слева направо, а справа налево, мы получим уже другую фазу.

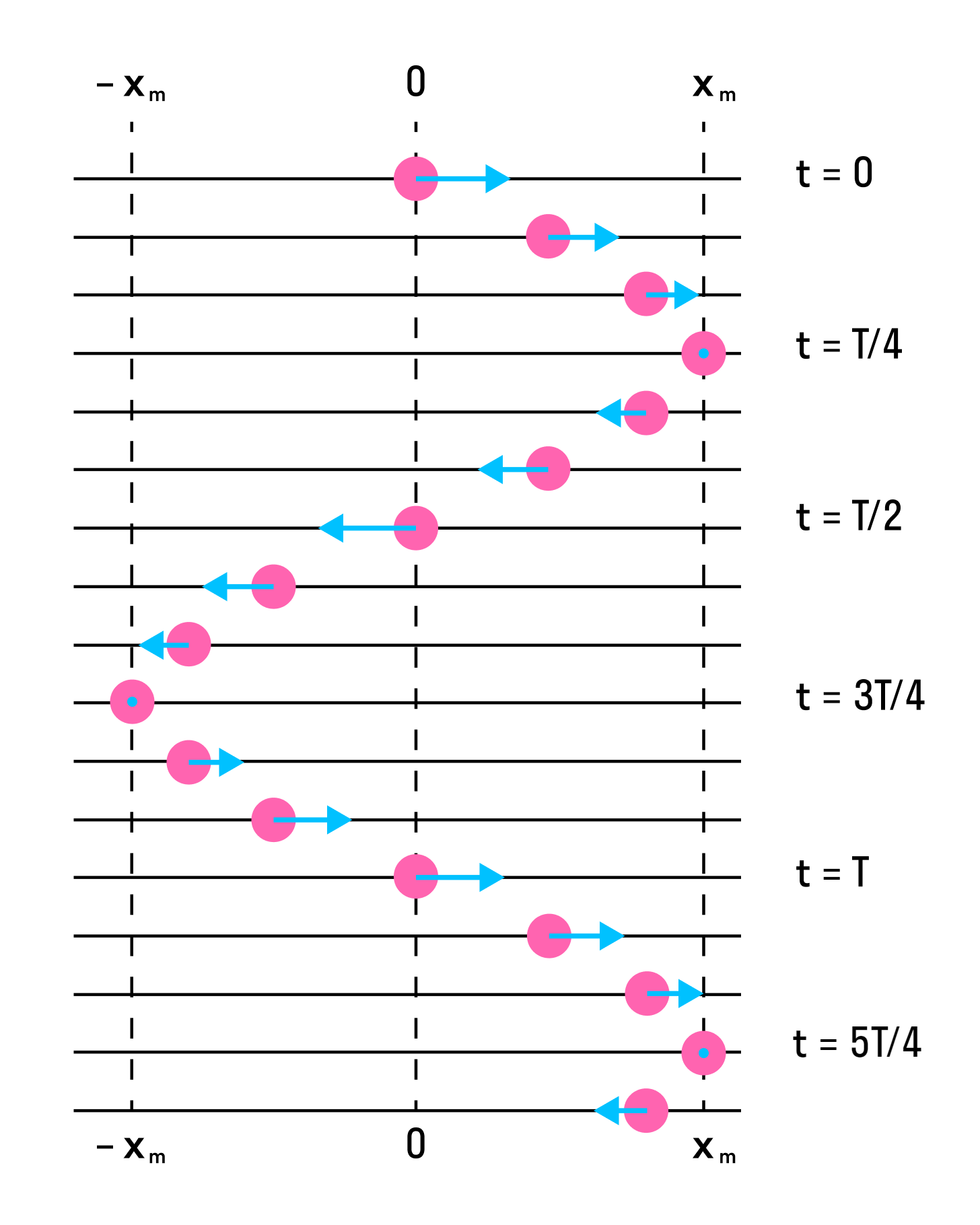
На рисунке ниже показаны положения тела через одинаковые промежутки времени при гармонических колебаниях. Такую картину можно получить при освещении колеблющегося тела короткими периодическими вспышками света (стробоскопическое освещение). Стрелки изображают векторы скорости тела в различные моменты времени.

Если изменить период, начальную фазу или амплитуду колебания, графики тоже изменятся.

На рисунке ниже во всех трех случаях для синих кривых начальная фаза равна нулю, а в последнем (с) — красная кривая имеет меньшую начальную фазу.

В первом случае (а) красная кривая описывает колебание, у которого амплитуда больше колебания, описанного синей линией.

Во втором случае (b) красная кривая отличается от синей только значением периода — у красной период в два раза меньше.

Математический маятник

Математический маятник — отличный пример гармонических колебаний. Если мы подвесим шарик на нити, то это еще не будет математическим маятником — пока он только физический.

Математическим этот маятник станет, если размеры шарика много меньше длины нити (тогда этими размерами можно пренебречь и рассматривать шарик как материальную точку), растяжение нити очень мало, а масса нити во много раз меньше массы шарика.

Математическим маятником называется система, которая состоит из материальной точки массой m и невесомой нерастяжимой нити длиной l, на которой материальная точка подвешена, и которая находится в поле силы тяжести (или других сил).

Период малых колебаний математического маятника в поле силы тяжести Земли определяется по формуле:

Формула периода колебания математического маятника

l — длина нити [м]

g — ускорение свободного падения [м/с 2 ]

На планете Земля g = 9,8 м/с 2

Пружинный маятник

Пружинный маятник — это груз, прикрепленный к пружине, массой которой можно пренебречь.

В пружинном маятнике колебания совершаются под действием силы упругости.
Пока пружина не деформирована, сила упругости на тело не действует.

Формула периода колебания пружинного маятника

m — масса маятника [кг]

k — жесткость пружины [Н/м]

Закон сохранения энергии для гармонических колебаний

Физика — такая клевая наука, в которой ничего не исчезает бесследно и не появляется из ниоткуда. Эту особенность описывает закон сохранения энергии.

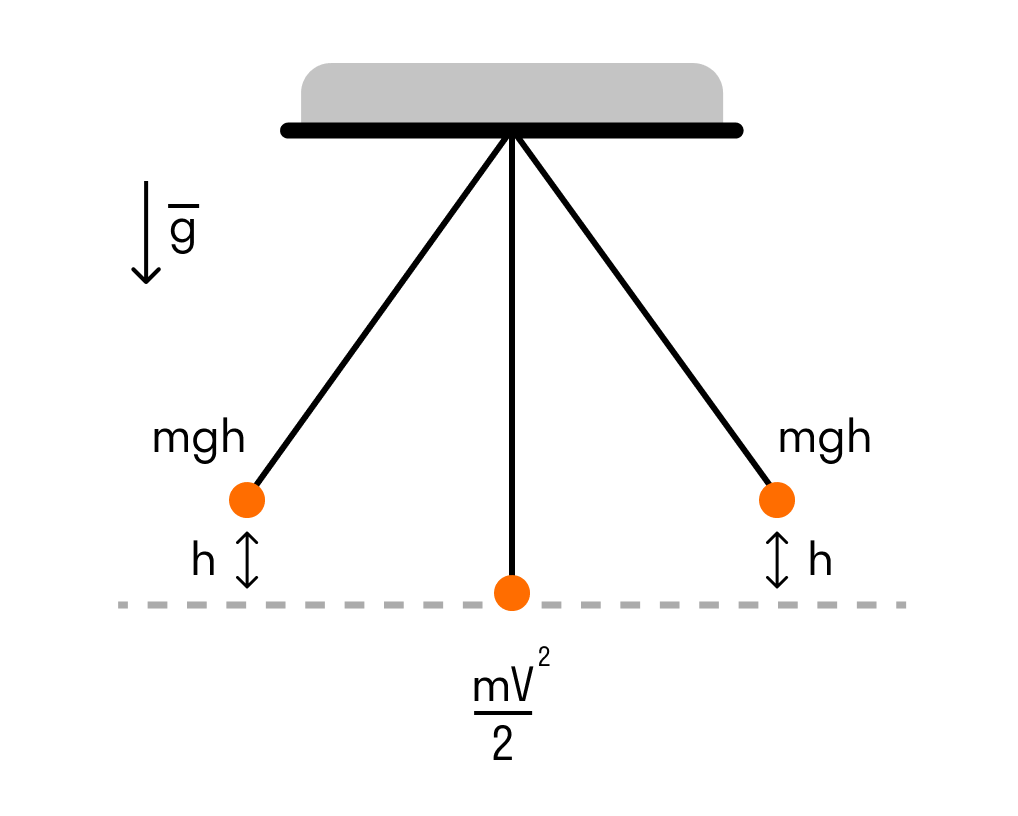
Рассмотрим его на примере математического маятника.

• Когда маятник отклоняют на высоту h, его потенциальная энергия максимальна.
• Когда маятник опускается, потенциальная энергия переходит в кинетическую. Причем в нижней точке, где потенциальная энергия равна нулю, кинетическая энергия максимальна и равна потенциальной энергии в верхней точке. Скорость груза в этой точке максимальна.

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!