Дифференциальные уравнения. Определение:дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х
Определение:дифференциальным уравнением называется уравнение, связывающее между собой независимую переменную х, искомую функцию уи ее производные или дифференциалы.
Решением (или интегралом) дифференциального уравнения, называется такая функция, которая обращает это уравнение в тождество.
Общим решением (или интегралом)дифференциального уравнения называется такое решение, в которое входит столько независимых произвольных постоянных, каков порядок уравнения.
Частным решениемдифференциального уравнения называется решение, полученное из общего при различных числовых значениях произвольных постоянных. Значения произвольных постоянных находятся при определенных начальных условиях.
Дифференциальным уравнением первого порядка называется уравнение, в которое входят производные (или дифференциалы) не выше первого порядка.
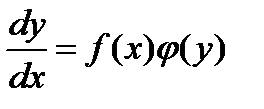
Уравнение вида называется дифференциальным уравнением с разделяющимися переменными.
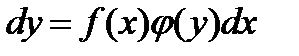
Затем интегрируем обе части данного равенства:
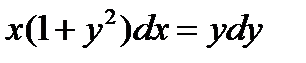
Найти общее решение уравнения:
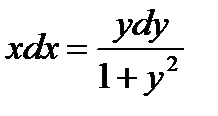
Проинтегрируем обе части равенства:
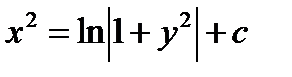
Линейные уравнения.
Линейные уравнения – это уравнения вида:
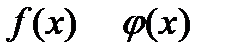
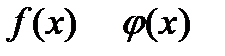
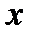
и могут быть постоянными величинами.
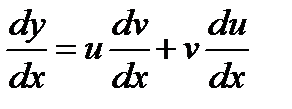
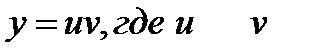
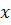
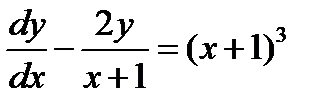
Найти общее решение уравнения
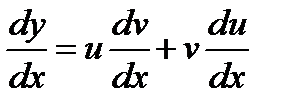
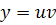
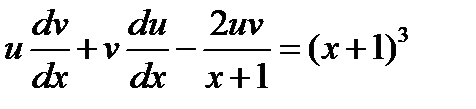
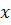
Т. к. одну из вспомогательных функций 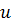
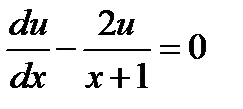
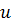
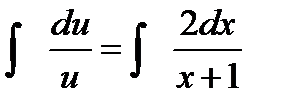
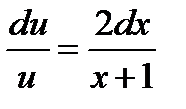
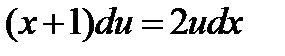
(произвольную постоянную С принимаем равной нулю, так как находим одно из частных решений).
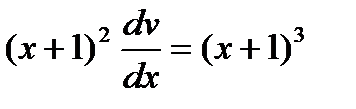
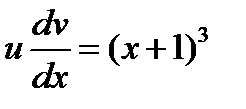
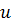

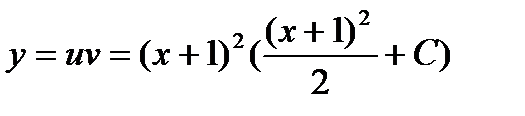
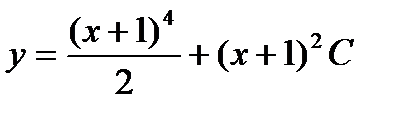
Зная 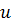
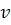
Ряды.
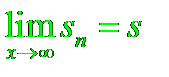
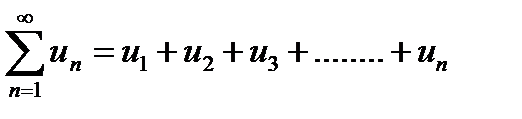
Если этот предел существует и конечен , то ряд называют сходящимся.
Если же этот предел бесконечен или вовсе не существует, то ряд называют расходящимся.
Условие 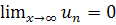
Признаки сходимости рядов:
Пусть даны два ряда с положительными членами
И пусть для всех значений k =1, 2 … выполняются неравенства
А) если 1 ряд сходится, то и сходится 2 ряд;
Б) если 2 ряд расходится, то и расходится 1 ряд
2. Признаки Даламбера и Коши
Пусть дан ряд с положительными членами
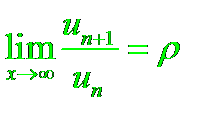
И пусть существует конечный предел
а) если 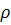
г) если 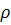
Пусть дан ряд с положительными членами
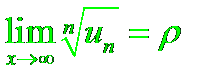
И пусть существует конечный предел
а) если 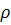
г) если 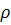
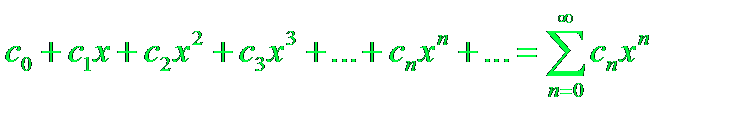
Степенным рядом называют ряд вида:
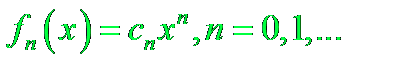
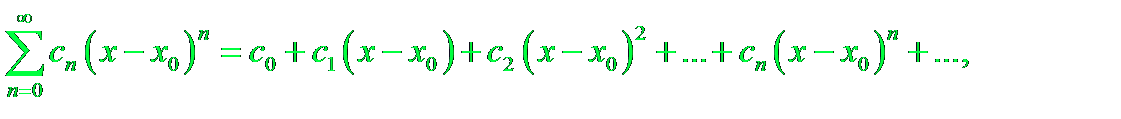
Называемые степенными рядами в точке х0.
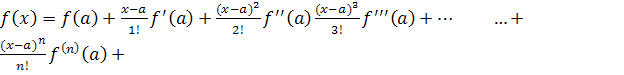
Называется рядом Тейлора.
Если в ряде Тейлора положим 
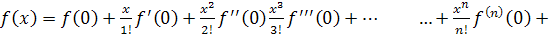
Разложить функцию в ряд Маклорена.
t wx:val=»Cambria Math»/> x «>
Решение. Найдем производные и значения функции и производных в точке х=0:
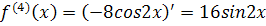
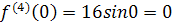
Контрольные задания.
1.
11. Вычислить угол между векторами s w:val=»28″/> a «> 
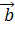
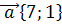
12. Вычислить длину вектора 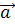

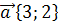
13. Вычислить длину вектора 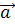

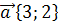
14. Вычислите проекцию вектора 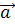
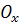
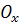

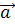
15. Даны векторы 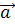


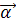

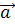

16. Даны векторы 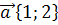
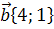
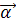

17. Дано векторы | 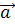
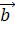
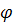
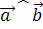
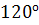
Найти: а) 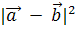
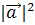
18. Построить вектор 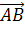
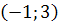
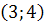
19. Найти скалярное произведение векторов 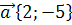
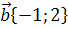
20. Найти модуль вектора 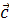
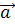

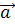
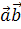
Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные
1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные .
Символически дифференциальное уравнение выглядит:
F(x,y,y’,y’’…,y ( n ) )=0 или 
2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение:
F(x,y,y’)=0- дифференциальное уравнение первого порядка.
F(x,y,y’,y’’)=0- дифференциальное уравнение второго порядка.
3. Решением дифференциального уравнения называется всякая функция 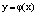
Для того чтобы решить дифференциальное уравнение надо его проинтегрировать.
Дифференциальное уравнение первого порядка.
Общее и частное решения.
Это уравнение можно привести к виду y’=f(x,y).
После вычисления возникает постоянная С. Поэтому решение фактически зависит не только от х, но и от С, т.е. y=f(x,C). Придавая С различные значения, мы получаем множество различных решений дифференциального уравнения. Эти решения (y=f(x,C)) называются общим решением дифференциального уравнения.
Придавая С различные значения получаем различные решения дифференциального уравнения. Так как С имеет бесконечное множество значений, то и решений будет бесконечное множество (которые отличаются друг от друга путем сдвига на несколько единиц).
Геометрически общее решение представляет собой семейство кривых на координатной плоскости ХОУ.
Пусть в дифференциальном уравнении заданы дополнительные условия, что при х=х0 функция принимает значение у=у0. Это дополнительное условие называется начальным условием и записывается: а). у=у0 при х=х0; б). 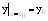
Геометрически начальное условие означает некоторую точку (х0,у0) на плоскости ХОУ.
Подставляя 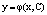
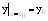
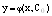
Геометрически частное решение обозначает: начальное условие задает некоторую точку на плоскости и из семейства кривых (общее решение) выбирается та единственная кривая, которая проходит через эту точку.
Теорема существования и единственности решения дифференциального уравнения (теорема Коши).
Если в дифференциальном уравнении y=f(x,y) функция f(x,y) и ее частная производная 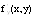
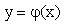
Геометрически смысл заключается в следующем: каждой точке (х0,у0) области Д соответствует только одна интегральная кривая, проходящая через эту точку (каждой точке соответствует только одно частное решение).
Замечание. “Найти частное решение”=“Решить задачу Коши”.
Существует 4 вида дифференциальных уравнений первого порядка.
1. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальные уравнения первого порядка в общем виде можно записать либо через производные F(x,y,y’)=0, либо через дифференциалы
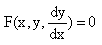
Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:
— 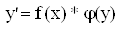
— 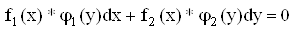
В этих уравнениях в произведениях стоят функции, каждая из которых зависит от одной переменной (х или у). Т.е. уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая.
Замечание. При решении дифференциальное уравнение ответу можно придать различную форму в зависимости от того, как записана произвольная постоянная С.
—
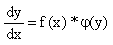

—
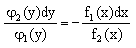
Однородные дифференциальные уравнения первого порядка
Функция f(x,y) называется однородной функцией n–го измерения, если при любом 
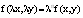
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy;
Однородное уравнение всегда можно привести к виду 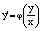
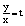
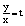
Линейные дифференциальные уравнения
ЛДУ- уравнения вида y’+P(x)y=Q(x)– первого порядка относительно у и у’.
Для решения ЛДУ применяем замену: y=UV, тогда y’=U’V+UV’
Далее U’+P(x)U=0, получаем два уровнения с разделяющимися переменными:
1). U’+P(x)U=0 находим U. 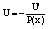
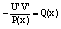
Замечание. Выражение, стоящее в скобках, можно прировнять к нулю, т.к. одну из функций можно взять произвольной, другую – определяем на основании ЛДУ.
УБ- дифференциальные уравнения вида y’+P(x)y=Q(x)*y n , где
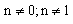
УБ решаются так же, как и линейные.
Дифференциальные уравнения второго порядка
Дифференциальные уравнения второго порядка в общем виде записываются: F(x,y,y’,y’’)=0
Как и в случае дифференциальных уравнений первого порядка для решения дифференциальных уравнений второго порядка существуют общее и частное решения. Но, если для дифференциальных уравнений первого порядка решение зависело от одной константы С, то для дифференциальных уравнений второго порядка решение зависит от двух постоянных: 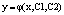
Если заданы начальные условия (у=у0, у=у0 при х=х0), то получаем частное решение, удовлетворяющее этим начальным условиям.
Начальные условия так же могут задаваться в виде:
у=у0 при х=х0; у=у1 при х=х1.
Три случая понижения порядка
1. Случай непосредственного интегрирования
y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.
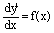
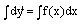
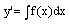
Высшая математика
Дифференциальное уравнение (ДУ) — это уравнение, связывающее между собой независимую переменную х, искомую функцию y = f(x) и ее производные y′, y′′,… y (n) .
Обыкновенное ДУ — это дифференциальное уравнение с одной независимой переменной.
Порядок ДУ — это порядок наивысшей производной, входящей в уравнение.
Решение или интеграл ДУ — это всякая функция y = f(x), которая, будучи подставлена в ДУ, превращает его в тождество.
График решения — это интегральная кривая.
Основная задача интегрального исчисления — это нахождение решения ДУ.
Общее решение ДУ F(x, y, y′,…, y (n) ) = 0 — это такое решение y = f(x, c1, c2, …, cn), которое содержит столько независимых произвольных постоянных ci, i = 1, 2, … n, каков порядок этого ДУ.
Общий интеграл ДУ — это общее решение заданное в неявном виде Ф(x, y, c1, c2, …, cn) = 0.
Частное решение ДУ — это всякое решение ДУ, которое получается из общего при определенных значениях произвольных постоянных.
Решение дифференциальных уравнений, примеры здесь
- Решение ДУ первого порядка
 — уравнение с разделяющимися переменными.
— уравнение с разделяющимися переменными. Метод решения: непосредственное интегрирование.
 — однородное уравнение.
— однородное уравнение. Метод решения:
 .
. — обобщенное однородное уравнение.
— обобщенное однородное уравнение. Метод решения:


 .
. — линейное по y(x) уравнение.
— линейное по y(x) уравнение. Метод решения:

 — линейное по x(y) уравнение.
— линейное по x(y) уравнение. Метод решения:

 — уравнение Бернулли.
— уравнение Бернулли. Метод решения:

 — уравнение в полных дифференциалах.
— уравнение в полных дифференциалах. Метод решения: интегрирование системы

- Решение ДУ второго порядка, допускающих понижение порядка
Метод решения: последовательное интегрирование.
Метод решения:.
Метод решения:.
Метод решения:.
Метод решения:
- Решение ОЛДУ второго порядка с постоянными коэффициентами
- Корни характеристического уравнения:
D>0,, действительные, разные.
Вид общего решения:.
- Корни характеристического уравнения:
, действительные, равные, кратность 2.
Вид общего решения:.
- Корни характеристического уравнения:
, комплексные.
Вид общего решения:.
- Корни характеристического уравнения:
.
Вид общего решения:.
 .
.- ОЛДУ n-го порядка с постоянными коэффициентами
- Корни характеристического уравнения: действительные, разные k1≠k2≠k3≠…≠kn.
Вид общего решения или вклад в общее решение: - Корни характеристического уравнения: действительные, кратности r≤n, k1=k2=k3=…=kr=k.
Вид общего решения или вклад в общее решение: - Корни характеристического уравнения: комплексные, разные,
α1≠α2≠…≠αn, β1≠β2≠…≠βn.
Вид общего решения или вклад в общее решение: - Корни характеристического уравнения: комплексные кратности r, k1=k2=…=kr=k=α+iβ.
Вид общего решения или вклад в общее решение:


- Решение НЛДУy′′ + py′ + qy = f(x)
y = yO.O. + yЧ.Н. = ȳ + ỹ
Метод неопределенных коэффициентов
Метод вариации произвольной постоянной 

Принцип суперпозиции
Если
- Решение НЛДУ n-го порядка
y n + a1y n-1 + a2y n-2 + … + an = f(x), yO.Н. = yO.О. + yЧ.Н.
Метод неопределенных коэффициентов
Метод вариации произвольной постоянной 
http://kazedu.com/referat/180434/1
http://matematika.electrichelp.ru/differencialnye-uravneniya/
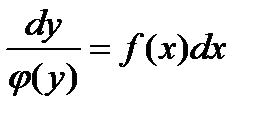
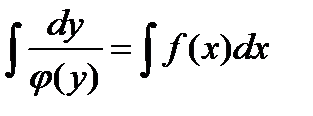
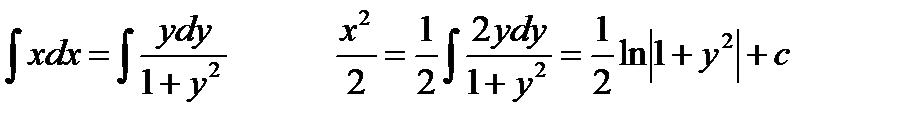
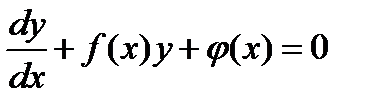

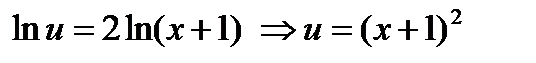


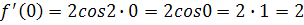
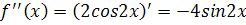
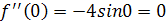
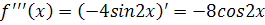
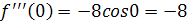
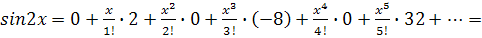
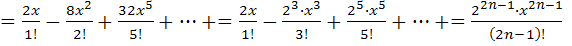
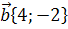
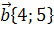
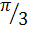
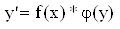
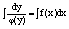
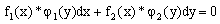
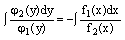
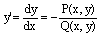
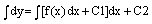


 .
.
 .
.
 .
.

 , действительные, разные.
, действительные, разные.  .
. , действительные, равные, кратность 2.
, действительные, равные, кратность 2.  .
. , комплексные.
, комплексные.  .
. .
.  .
.







