Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные
1. Дифференциальное уравнение- уравнение , связывающее независимую переменную х, искомую функцию f(x) и ее производные .
Символически дифференциальное уравнение выглядит:
F(x,y,y’,y’’…,y ( n ) )=0 или 
2. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение:
F(x,y,y’)=0- дифференциальное уравнение первого порядка.
F(x,y,y’,y’’)=0- дифференциальное уравнение второго порядка.
3. Решением дифференциального уравнения называется всякая функция 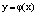
Для того чтобы решить дифференциальное уравнение надо его проинтегрировать.
Дифференциальное уравнение первого порядка.
Общее и частное решения.
Это уравнение можно привести к виду y’=f(x,y).
После вычисления возникает постоянная С. Поэтому решение фактически зависит не только от х, но и от С, т.е. y=f(x,C). Придавая С различные значения, мы получаем множество различных решений дифференциального уравнения. Эти решения (y=f(x,C)) называются общим решением дифференциального уравнения.
Придавая С различные значения получаем различные решения дифференциального уравнения. Так как С имеет бесконечное множество значений, то и решений будет бесконечное множество (которые отличаются друг от друга путем сдвига на несколько единиц).
Геометрически общее решение представляет собой семейство кривых на координатной плоскости ХОУ.
Пусть в дифференциальном уравнении заданы дополнительные условия, что при х=х0 функция принимает значение у=у0. Это дополнительное условие называется начальным условием и записывается: а). у=у0 при х=х0; б). 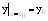
Геометрически начальное условие означает некоторую точку (х0,у0) на плоскости ХОУ.
Подставляя 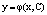
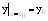
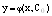
Геометрически частное решение обозначает: начальное условие задает некоторую точку на плоскости и из семейства кривых (общее решение) выбирается та единственная кривая, которая проходит через эту точку.
Теорема существования и единственности решения дифференциального уравнения (теорема Коши).
Если в дифференциальном уравнении y=f(x,y) функция f(x,y) и ее частная производная 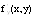
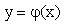
Геометрически смысл заключается в следующем: каждой точке (х0,у0) области Д соответствует только одна интегральная кривая, проходящая через эту точку (каждой точке соответствует только одно частное решение).
Замечание. “Найти частное решение”=“Решить задачу Коши”.
Существует 4 вида дифференциальных уравнений первого порядка.
1. Дифференциальные уравнения первого порядка с разделяющимися переменными.
Дифференциальные уравнения первого порядка в общем виде можно записать либо через производные F(x,y,y’)=0, либо через дифференциалы
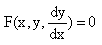
Дифференциальное уравнение- уравнение с разделяющимися переменными, если его можно представить в виде:
— 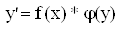
— 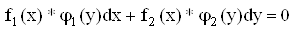
В этих уравнениях в произведениях стоят функции, каждая из которых зависит от одной переменной (х или у). Т.е. уравнение будет уравнением с разделяющимися переменными, если его можно преобразовать так, чтобы в одной его части была только одна переменная, а в другой – только другая.
Замечание. При решении дифференциальное уравнение ответу можно придать различную форму в зависимости от того, как записана произвольная постоянная С.
—
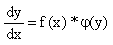

—
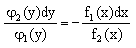
Однородные дифференциальные уравнения первого порядка
Функция f(x,y) называется однородной функцией n–го измерения, если при любом 
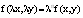
Дифференциальное уравнение y’=f(x,y) есть однородное, если функция f(x,y) является однородной функцией нулевого измерения.
Дифференциальное уравнение P(x,y)dx+Q(x,y)dy=0 однородное, если P(x,y) и Q(x,y) являются однородными функциями одного и того же измерения.
P(x,y)dx=-Q(x,y)dy;
Однородное уравнение всегда можно привести к виду 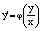
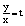
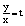
Линейные дифференциальные уравнения
ЛДУ- уравнения вида y’+P(x)y=Q(x)– первого порядка относительно у и у’.
Для решения ЛДУ применяем замену: y=UV, тогда y’=U’V+UV’
Далее U’+P(x)U=0, получаем два уровнения с разделяющимися переменными:
1). U’+P(x)U=0 находим U. 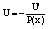
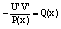
Замечание. Выражение, стоящее в скобках, можно прировнять к нулю, т.к. одну из функций можно взять произвольной, другую – определяем на основании ЛДУ.
УБ- дифференциальные уравнения вида y’+P(x)y=Q(x)*y n , где
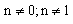
УБ решаются так же, как и линейные.
Дифференциальные уравнения второго порядка
Дифференциальные уравнения второго порядка в общем виде записываются: F(x,y,y’,y’’)=0
Как и в случае дифференциальных уравнений первого порядка для решения дифференциальных уравнений второго порядка существуют общее и частное решения. Но, если для дифференциальных уравнений первого порядка решение зависело от одной константы С, то для дифференциальных уравнений второго порядка решение зависит от двух постоянных: 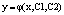
Если заданы начальные условия (у=у0, у=у0 при х=х0), то получаем частное решение, удовлетворяющее этим начальным условиям.
Начальные условия так же могут задаваться в виде:
у=у0 при х=х0; у=у1 при х=х1.
Три случая понижения порядка
1. Случай непосредственного интегрирования
y’’=f(x)- решение этого уравнения находится путем двукратного интегрирования.
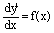
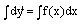
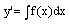
Дифференциальные уравнения первого порядка. Понятие о методе Рунге—Кутта
Содержание:

По этой ссылке вы найдёте полный курс лекций по математике:
Обыкновенным дифференциальным уравнением называется уравнение вида связывающее независимую переменную х, искомую функцию у = у(х) и ее производные у'(х),у»(х)>. у(п)(ж) (наличие хотя бы одной производной обязательно). Здесь — заданная функция своих аргументов. Замечание. Обозначения зависимой и независимой переменных через х и у, используемые в приведенном определении, не являются жесткими; часто в качестве независимой удобно брать переменную t, иными буквами обозначают и зависимую переменную (см. ниже пример 2).
В обыкновенном дифференциальном уравнении искомая функция у = у(х) есть функция одной независимой переменной х. Если искомая функция есть функция двух (и более) независимых переменных, то имеем дифференциальное уравнение с частными производными. В этой и двух следующих главах мы будем рассматривать только обыкновенные дифференциальные уравнения.
Простейшим дифференциальным уравнением является уравнение вида ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА Эквивалентные дифференциальные уравнения Задача Коши еорема существования и единственности решения задачи Коши для уравнения Приближенные методы интегрирования уравнения Метод последовательных приближений Численные методы решения задачи Коши Метод Эйлера Понятие о методе Рунге—Кутта где f(x) — известная непрерывная на некотором интервале (а, 6) функция, а у = у(х) — искомая функция.
С таким уравнением мы уже встречались в интегральном исчислении, когда поданной функции f(x) требовалось найти ее первообразную F(x). Как известно, всякая функция, удовлетворяющая уравнению (2), имеет вид где F(x) — какая-нибудь первообразная для функции /(ж) на интервале (а, 6), а С — произвольная постоянная. Таким образом, искомая функция у = у(х) определяется из уравнения (2) неоднозначно. Порядком дифференциального уравнения называется порядок наивысшей производной, входящей в уравнение.
Например, — дифференциальное уравнение 1-го порядка; дифференциальное уравнение 2-го порядка; — дифференциальное уравнение пятого порядка. Решением дифференциального уравнения n-го порядка на интервале (а, Ь) называется всякая функция у = (р(х), имеющая на этом интервале производные до n-го порядка включительно и такая, что подстановка функции у = tp(x) и ее производных в дифференциальное уравнение обращает последнее в тождество по х на интервале (а, Ь).
Например, функция у = sin х является решением дифференциального уравнения второго порядка на интервале (-оо, +оо). В самом деле, . Подставив в данное уравнение найденные значения у и у», получим — Задача. Найти совпадающие решения двух дифференциальных уравнений (не решая самих уравнений): График решения дифференциального уравнения называется интегральной кривой этого уравнения. Процесс нахождения решения дифференциального уравнения называется интегрированием дифференциального уравнения.
К составлению и интегрированию дифференциальных уравнений приводят многочисленные задачи как самой математики, так и других наук (физики, химии, биологии и т. п.). Пример 1. Найти такую кривую, чтобы тангенс угла наклона касательной в каждой ее точке численно равнялся ординате точки касания. Пусть — уравнение искомой кривой.
Как известно, , значит, определяющее свойство кривой есть — дифференциальное уравнение первого порядка.
Нетрудно видеть, что функция _ть решение этого уравнения. Оно также имеет очевидное решение у = 0. Кроме того, решениями оудут функции где С — произвольная постоянная, так что уравнение имеет бесконечное множество решений. ^ Пример 2. Найти закон прямолинейного движения материальной точки, движущейся с постоянным ускорением а.
А Требуется найти формулу з = s(t). выражающую пройденный путь как функцию времени. По условию имеем — дифференциальное уравнение второго порядка. Последовательно находим: Произвольные постоянные можно определить, если положить В самом деле, полагая первом из соотношений (*). получаем , откуда — Из второго соотношения (*) при t = tq имеем откуда Подставляя найденные значения С\ и С? в выражение для функции *(f). приходим к известному закону движения материальной точки с постоянным ускорением: § 2. Эквивалентные дифференциальные уравнения.
Задача Коши Пусть имеем дифференциальное уравнение первого порядка Если в этом уравнении удается выразить производную у’ через х и у, то получаем уравнение разрешенное относительно производной. Здесь / — заданная функция своих аргументов. Наряду с уравнением (1) рассматривают эквивалентное ему дифференциальное уравнение или уравнение более общего вида получаемое из (Г) путем умножения на некоторую функцию известные функции своих аргументов).
Два дифференциальных уравнения называются эквивалентными в некоторой области D изменения величин х, у, у’, если всякое решение у(х) 6 D одного из этих уравнений является решением другого уравнения и наоборот. При преобразовании дифференциальных уравнений надо следить за тем, чтобы преобразованное уравнение было эквивалентным исходному. Если дифференциальное уравнение имеет решение, то, как правило, множество его решений оказывается бесконечным.
Впрочем, дифференциальное уравнение имеет только одно решение а уравнение Чтобы выделить определенное решение уравнения (1), надо задать начальное условие, которое заключается в том, что при некотором значении независимой переменной х заранее дано значение уо искомой функции у(х): Геометрически это означает, что задается точка Мо(х0, уо), через которую должна проходить искомая интегральная кривая.
Возможно вам будут полезны данные страницы:
Задачу отыскания решения у(х) уравнения (1), удовлетворяющего начальному условию (2), называют задачей Коши (начальной задачей) для уравнения (1). §3. Теорема существования и единственности решения задачи Коши для уравнения Теорема 1 (существования и единственности решения). Пусть имеем дифференциальное уравнение и пусть функция f(x, у) определена в некоторой области D на плоскости хОу. Выберем произвольную точку Мо(хо,уо) € D.
| Если существует окрестность Q этой |
точки, в которой функция 1) непрерывна по совокупности аргументов; 2) имеет ограниченную частную производную ^, то найдется интервал оси Ох, на котором существует, и притом единственная, функция у = , являющаяся решением уравнения(1) и принимающая при х = жо значение уо (рис. Геометрически это означает, что через точку ) проходит одна и только одна интегральная кривая уравнения (1). Теорема 1 имеет локальный характер: она гарантирует существование единственного решения у = tp(x) уравнения (1) лишь в достаточно малой окрестности точки х0-
Из теоремы 1 вытекает, что уравнение (1) имеет бесконечное множество различных решений (например, одно решение, график которого проходит через точку (жо, г/о); другое решение, когда график проходит через точку Пример 1. В уравнении функция определена и непрерывна во всех точках плоскости хОу и имеет всюду щ = 1. В силу теоремы 1 через каждую точку (xq, уо) плоскости хОу проходит единственная интегральная кривая этого уравнения. Пример 2.
В уравнении функция определена и непрерывна на всей плоскости хОу. Здесь так что второе условие теоремы 1 нарушается в точках оси Ох. Нетрудно проверить, что функция где С — любая постоянная, является решением данного уравнения. Кроме того, уравнение имеет очевидное решение Если искать решения этого уравнения, соответствующие условию у(0) = 0, то таких решений найдется бесчисленное множество, в частности, следующие (рис. 2): Таким образом, через каждую точку оси Ох проходят по крайней мере две интегральные кривые и, следовательно, в точках Этой оси нарушается единственность.
Если взять точку Л/|(1, 1), то в достаточно малой ее окрестности выполнены все условия теоремы 1. Следовательно, через данную точку в малом квадрате П проходит единственная интегральная кривая ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА Эквивалентные дифференциальные уравнения Задача Коши еорема существования и единственности решения задачи Коши для уравнения Приближенные методы интегрирования уравнения Метод последовательных приближений Численные методы решения задачи Коши Метод Эйлера Понятие о методе Рунге—Кутта уравнения у’ = 3у >.
Если квадрат Q взять достаточно большим (подумайте, каким), то в нем единственность решения уже не будет иметь места. Это подтверждает локальный характер теоремы 1. Теорема 1 дает достаточные условия существования единственного решения уравнения у’ = . Это означает, что может существовать единственное решение у = у(х) уравнения у’ = f(x> у)* удовлетворяющее условию у\х=го = у0, хотя в точке (жо> уо) не выполняются условия 1) или 2) теоремы или оба вместе.
Пример 3:
Для уравнения имеем В точках оси Ох функции / и разрывны, причем Но через каждую точку (хо, 0) оси Ох проходит единственная интегральная кривая Замечание. Если отказаться от ограниченности , то получается следующая теорема существования решения. Теорема 2. Если функция f(x, у) непрерывна в некоторой окрестности точки (х0, уо), то уравнение имеет в этой окрестности по крайней мере одно решение , принимающее при х = х0 значение уо.
Теорема существом*и« и единственности решение задачи Кошм для уравнения Задача. Найти интегральную кривую уравнения проходящую через точку . Задача. Найти решение задачи Коши Определение 1. Общим решением дифференциального уравнения в некоторой области Q существования и единственности решения задачи Коши называется однопараметрическое семейство S функций у = ip(x, С), зависящих от переменной ж и одной произвольной постоянной С (параметра), такое, что 1) при любом допустимом значении постоянной С функция является решением уравнения (1): 2) каково бы ни было начальное условие .
Можно подобрать такое значение Со постоянной С, что решение у = Со) будет удовлетворять начальному условию При этом предполагается, что точка (жо, уо) принадлежит области П существования и единственности решения задачи Коши. Пример 4. Показать, что общим решением дифференциального уравнения является функция где С — произвольная постоянная. 4 В данном случае /, и условия теоремы 1 выполняются всюду. Следовательно, через каждую точку (zo, уо) плоскости хОу проходит единственная интегральная кривая данного уравнения. Проверим, что функция удовлетворяет условиям 1) и 2), содержащимся в определении общего решения.
Действительно, при любом С имеем так что у = х + С есть решение данного уравнения. Потребовав, чтобы при х = хо решение принимало значение уо, приходим к соотношению уо = х0 + Со, откуда Решение . или удовлетворяет поставленному начальному условию. Частным решением дифференциального уравнения (1) называется решение, получаемое из общего при каком-либо конкретном значении произвольной постоянной С (включая ±оо).
Таким образом, общее решение этого дифференциального уравнения можно определить как множество всех частных решений уравнения. В процессе интегрирования дифференциального уравнения мы часто приходим к уравнению неявно задающему общее решение уравнения. Уравнение (2) называют общим интегралом дифференциального уравнения (\). Уравнение где Со — некоторое конкретное значение постоянной С, называется частным интегралом. Замечание.
Название происходит от того, что для простейшего дифференциального уравнения вида его общее решение действительно записывается при помощи обычного неопределенного интеграла Пример. Общий интеграл уравнения имеет следующий вид или В дальнейшем для краткости мы будем иногда говорить, что решение уравнения проходит через некоторую точку Mq(xq, уо), если точка М0 лежит на графике этого решения.
Определение 2:
Решение дифференциального уравнения (1) называется особым, если в каждой его точке нарушается свойство единственности, т. е. если через каждую его точку (so, уо) кроме этого решения проходит и другое решение уравнения (1), не совпадающее в сколь угодно малой окрестности точки График особого решения называют особой интегральной кривой уравнения. Геометрически это — огибающая семейства интегральных кривых дифференциального уравнения, определяемых его общим интегралом1*.
Если для дифференциального уравнения (1) в некоторой области D на плоскости хОу выполнены условия теоремы 1, то через каждую точку (хо, уо) € D проходит единственная интегральная кривая уравнения. Эта кривая входит в однопа-раметрическое семейство кривых образующих общий интеграл уравнения (1), и получается из этого семейства при конкретном значении параметра С, т.е. является частным интегралом уравнения (1). Никаких других решений, проходящих через точку (жо> 2/о)> здесь быть не может.
Следовательно, для существования особого решения у уравнения (1) необходимо, чтобы не выполнялись условия теоремы 1. В частности, если правая часть уравнения (1) непрерывна в рассматриваемой области D, то особые решения могут проходить только через те точки, где производная Ц становится бесконечной. Напомним, что огибающей семейства кривых Ф(х, у, С) = 0 называется такая кривая, которая в каждой своей точке касается некоторой кривой семейства и каждого отрезка которой касается бесконечное множество кривых из этого семейства.
Например, для уравнения ) функция / = Зу2/3 непрерывна всюду, но производная Ц обращается в бесконечность при у = 0. т.е. на оси Ох плоскости хОу. Уравнение (3) имеет общее решение — семейство кубических парабол — и очевидное решение проходящее через те точки, где производная ^ не ограничена. Решение у = 0 — особое, так как через каждую его точку проходит и кубическая парабола, и сама эта прямая у = 0 (см. рис. 2).
Таким образом, в каждой точке решения у = 0 нарушается свойство единственности. Особое решение у = 0 не получается из решения у = (х +С)3 ни при каком числовом значении параметра С (включая ±оо). Из теоремы 1 можно вывести только необходимые условия для особого решения. Множество тех точек, где производная не ограничена, если оно является кривой, может и не быть особым решением уже потому, что эта кривая, вообще говоря, не является интегральной кривой уравнения (1).
Если, например, вместо уравнения (3) взять уравнение то в точках прямой у = 0 по-прежнему нарушается условие ограниченности производной ^, но эта прямая, очевидно, не является интегральной кривой уравнения (4). Итак, чтобы найти особые решения уравнения (1), надо 1) найти множество точек, где производная ^ обращается в бесконечность; 2) если это множество точек образует одну или несколько кривых, проверить, являются ли они интегральными кривыми уравнения (1);
3) если это интегральные кривые, проверить, нарушается ли в каждой их точке свойство единственности. При выполнении всех этих условий найденная кривая представляет собой особое решение уравнения (1). Задача. Найти особые решения уравнения Сделать рисунок. §4. Приближенные методы интегрирования уравнения 4.1. Метод изоклин Пусть имеем дифференциальное уравнение где функция /(ж, у) в некоторой области D на плоскости хОу удовлетворяет условиям теоремы I.
Это уравнение определяет в каждой точке (ж, у) области D значение у’, т. е. угловой коэффициент касательной к интегральной кривой в этой точке. Говорят, что уравнение (1) определяет в области D поле направлений. Чтобы его построить, надо в каждой точке (ж0, уо) € D представить с помощью некоторого отрезка направление касательной к интегральной кривой в этой точке, определяемое значением /(жо, уо). Совокупность этих отрезков дает геометрическую картину поля направлений.
Задача интегрирования дифференциального уравнения (1) может быть теперь сформулирована так: найти такую кривую, чтобы касательная к ней в каждой точке имела направление, совпадающее с направлением поля в этой точке. Такое истолкование дифференциального уравнения и его интегрирования дает графический способ решения уравнения. Для построения интегральных кривых пользуются изоклинами. Изоклиной называется множество всех точек плоскости хОу, в которых касательные к искомым интегральным кривым имеют одно и то же направление (у’ = const).
Из этого определения следует, что семейство изоклин дифференциального уравнения (1) задается уравнением где к — числовой параметр. Если придать параметру к близкие числовые значения, можно найти достаточно густую сеть изоклин и приближенно построить интегральные кривые дифференциального уравнения. Пример 1. Проинтегрировать уравнение по способу изоклин. Семейство изоклин данного уравнения определяется уравнением ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ПЕРВОГО ПОРЯДКА Эквивалентные дифференциальные уравнения Задача Коши еорема существования и единственности решения задачи Коши для уравнения Приближенные методы интегрирования уравнения.
Метод последовательных приближений Численные методы решения задачи Коши Метод Эйлера Понятие о методе Рунге—Кутта Полагая , получаем изоклины , по которым строим интегральные кривые уравнения (рис. 4). Нулевая изоклина определяет множество возможных точек экстремума интегральных кривых (прямая х = О в примере 1).
Для большей точности построения интегральных кривых определяют направление вогнутости и точки перегиба этих кривых (если такие точки существуют). Для этого находят у» в силу уравнения (1): Знак правой части определяет знак у», т.е. направление вогнутости интегральных кривых. Линия, заданная уравнением есть множество всех возможных точек перегиба интегральных кривых. В примере 1 имеем поэтому все интегральные кривые обращены вогнутостью вверх, и точек перегиба интегральных кривых нет.
Метод последовательных приближений
Пусть имеем дифференциальное уравнение где функция f(x, у) в некоторой области D изменения х, у удовлетворяет условиям теоремы 1, и пусть точка (хо, уо) € D. Решение задачи Коши равносильно решению некоторого интегрального уравнения, т. е. уравнения, в которое неизвестная функция входит под знаком интеграла. В самом деле, пусть — решение уравнения (2), заданное в некоторой окрестности точки х0 и удовлетворяющее начальному условию (3).
Тогда при имеет место тождество Проинтегрируем это тождество по х Отсюда учитывая (3), получаем так что решение y(x) задачи Коши удовлетворяет интегральному уравнению (4) Обратно: если непрерывная функция , удовлегворяет интегральному уравнению (4), то, как легко проверить, у(х) является решением задачи Коши (2)-(3). Решение интегрального уравнения (4) для всех х, достаточно близких к хо» может быть построено методом последовательных приближений по формуле причем в качестве (po(t) можно взять любую непрерывную на отрезке функцию, в частности, ( Прммер 2.
Методом последовательных приближений решить задачу Коши Сводим данную задачу к интегральному уравнению Выбирая за нулевое приближение функцию последовательно находим: Легко видеть, что функция у = ех есть решение задачи. 4.3. Численные методы решения задачи Коши Метод Эйлера Пусть требуется найти приближенное решение дифференциального уравнения удовлетворяющее начальному условию.
Будем предполагать, что в некотором прямоугольнике функция f(x, у) непрерывна и имеет непрерывные частные производные достаточно высокого порядка по всем аргументам, так что решение задачи Коши (1)-(2) существует, единственно и является функцией, дифференцируемой достаточное число раз. Численное решение задачи состоит в построении таблицы приближенных значений , уп решения задачи в точках Чаще всего выбирают . Точки хк называют узлами сетки, а величину — шагом сетки.
Геометрически искомая интегральная кривая у = у(х), проходящая через точку заменяется ломаной Эйлера MqM\Mi . с вершинами в точках Метод Эйлера относится к группе одно-шаговых методов, в которых для вычисления точки требуется знание только предыдущей вычисленной точки . Для оценки погрешности метода на одном шаге сетки разложим точное решение в окрестности узла х = Хк по формуле Тейлора Сравнение формул () показывает, что они совпадают до членов первого порядка по h включительно, а погрешность формулы (4) равна 0(h2). Поэтому говорят, что метод Эйлера имеет первый порядок.
Пример. Методом Эйлера решить задачу Коши на отрезке с шагом В данном случае . Пользуясь формулой последовательно находим Результаты вычислений сведем в таблицу Точное решение Замечание. Если рассмотреть задачу Коши на любом отрезке с любым шагом , то получим и т.д., так что в этом случае ломаная Эйлера «распрямляется» и совпадает с прямой точным решением поставленной задачи Коши. Понятие о методе Рунге—Купа Метод Эйлера весьма прост, но имеет низкую точность.
Точность решения можно повысить путем усложнения разностной схемы. Весьма распространенными на практике являются схемы Рунге—Кутта. Пусть опять требуется решитьзадачу Коши . Будем строить таблицу приближенных значенийу решения уравнения вточках(узлах сетки). Рассмотрим схему равноотстоящих узлов — шаг сетки. В методе Рунге—Кутта величины yi+\ вычисляются по следующей схеме
Присылайте задания в любое время дня и ночи в ➔
Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.
Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.
Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.
Высшая математика
Дифференциальное уравнение (ДУ) — это уравнение, связывающее между собой независимую переменную х, искомую функцию y = f(x) и ее производные y′, y′′,… y (n) .
Обыкновенное ДУ — это дифференциальное уравнение с одной независимой переменной.
Порядок ДУ — это порядок наивысшей производной, входящей в уравнение.
Решение или интеграл ДУ — это всякая функция y = f(x), которая, будучи подставлена в ДУ, превращает его в тождество.
График решения — это интегральная кривая.
Основная задача интегрального исчисления — это нахождение решения ДУ.
Общее решение ДУ F(x, y, y′,…, y (n) ) = 0 — это такое решение y = f(x, c1, c2, …, cn), которое содержит столько независимых произвольных постоянных ci, i = 1, 2, … n, каков порядок этого ДУ.
Общий интеграл ДУ — это общее решение заданное в неявном виде Ф(x, y, c1, c2, …, cn) = 0.
Частное решение ДУ — это всякое решение ДУ, которое получается из общего при определенных значениях произвольных постоянных.
Решение дифференциальных уравнений, примеры здесь
- Решение ДУ первого порядка
 — уравнение с разделяющимися переменными.
— уравнение с разделяющимися переменными. Метод решения: непосредственное интегрирование.
 — однородное уравнение.
— однородное уравнение. Метод решения:
 .
. — обобщенное однородное уравнение.
— обобщенное однородное уравнение. Метод решения:


 .
. — линейное по y(x) уравнение.
— линейное по y(x) уравнение. Метод решения:

 — линейное по x(y) уравнение.
— линейное по x(y) уравнение. Метод решения:

 — уравнение Бернулли.
— уравнение Бернулли. Метод решения:

 — уравнение в полных дифференциалах.
— уравнение в полных дифференциалах. Метод решения: интегрирование системы

- Решение ДУ второго порядка, допускающих понижение порядка
Метод решения: последовательное интегрирование.
Метод решения:.
Метод решения:.
Метод решения:.
Метод решения:
- Решение ОЛДУ второго порядка с постоянными коэффициентами
- Корни характеристического уравнения:
D>0,, действительные, разные.
Вид общего решения:.
- Корни характеристического уравнения:
, действительные, равные, кратность 2.
Вид общего решения:.
- Корни характеристического уравнения:
, комплексные.
Вид общего решения:.
- Корни характеристического уравнения:
.
Вид общего решения:.
 .
.- ОЛДУ n-го порядка с постоянными коэффициентами
- Корни характеристического уравнения: действительные, разные k1≠k2≠k3≠…≠kn.
Вид общего решения или вклад в общее решение: - Корни характеристического уравнения: действительные, кратности r≤n, k1=k2=k3=…=kr=k.
Вид общего решения или вклад в общее решение: - Корни характеристического уравнения: комплексные, разные,
α1≠α2≠…≠αn, β1≠β2≠…≠βn.
Вид общего решения или вклад в общее решение: - Корни характеристического уравнения: комплексные кратности r, k1=k2=…=kr=k=α+iβ.
Вид общего решения или вклад в общее решение:


- Решение НЛДУy′′ + py′ + qy = f(x)
y = yO.O. + yЧ.Н. = ȳ + ỹ
Метод неопределенных коэффициентов
Метод вариации произвольной постоянной 

Принцип суперпозиции
Если
- Решение НЛДУ n-го порядка
y n + a1y n-1 + a2y n-2 + … + an = f(x), yO.Н. = yO.О. + yЧ.Н.
Метод неопределенных коэффициентов
Метод вариации произвольной постоянной 
http://natalibrilenova.ru/differentsialnyie-uravneniya-pervogo-poryadka-ponyatie-o-metode-runge-kutta-/
http://matematika.electrichelp.ru/differencialnye-uravneniya/
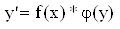
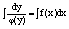
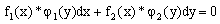
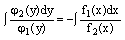
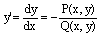















 .
.
 .
.
 .
.

 , действительные, разные.
, действительные, разные.  .
. , действительные, равные, кратность 2.
, действительные, равные, кратность 2.  .
. , комплексные.
, комплексные.  .
. .
.  .
.







