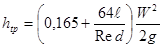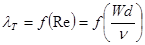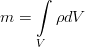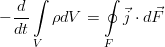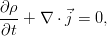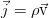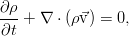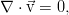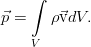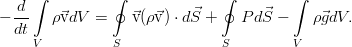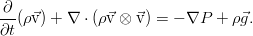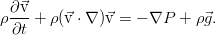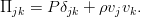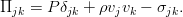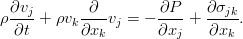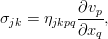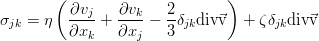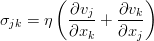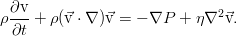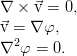Уравнение течения вязкой жидкости по трубе

Уравнение течения вязкой жидкости по трубе

webkonspect.com — сайт, с элементами социальной сети, создан в помощь студентам в их непростой учебной жизни.

Здесь вы сможете создать свой конспект который поможет вам в учёбе.

Чем может быть полезен webkonspect.com:

• простота создания и редактирования конспекта (200 вопросов в 3 клика).
• просмотр конспекта без выхода в интернет.
• удобный текстовый редактор позволит Вам форматировать текст, рисовать таблицы, вставлять математические формулы и фотографии.
• конструирование одного конспекта совместно с другом, одногрупником.
• webkonspect.com — надёжное место для хранения небольших файлов.

Уравнение Бернулли для потока вязкой жидкости

При движении вязкой жидкости вдоль твердой стенки, например, в трубе происходит торможение потока вследствие влияния вязкости и в результате сил молекулярного сцепления между жидкостью и стенкой. Реализуется неравномерное распределение скоростей: у стенки скорость потока уменьшается до нуля (у смачиваемой жидкости), а в центральной части потока она максимальна (это применительно к течению в трубе). Кроме того движение вязкой жидкости часто сопровождается вращением макрочастиц жидкости, вихреобразованием и перемешиванием. Все это требует затрат энергии, поэтому удельная энергия жидкости (т.е. полный напор) не остается постоянной, как в случае идеальной жидкости, а постепенно расходуется на преодоление сопротивлений и, следовательно, уменьшается вдоль потока. Сказанное можно выразить следующим балансовым уравнением:

где Н_ср1 и Н_ср2 – средние значения полного напора в сечении 1 и 2 соответственно, ∑h – суммарная потеря напора (удельной энергии жидкости) на участке между рассматриваемыми сечениями.

Используя это уравнение, запись уравнения Бернулли для случая течения вязкой жидкости представляется в следующем виде

, (5)

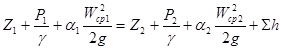
где Σh – суммарная потеря удельной энергии жидкости (напора) на участке между рассматриваемыми сечениями.

Энергия, теряемая жидкостью на рассматриваемом участке течения, не исчезает бесследно, а превращается в другую форму – тепловую. Эта энергия непрерывно рассеивается, поэтому повышение температуры жидкости практически мало заметно.

Гидравлические потери (общие сведения). Потери напора или, как их часто называют, гидравлические потери зависят от формы, размеров и шероховатости канала (трубы), от скорости течения и вязкости жидкости, но практически не зависят от абсолютного значения давления в жидкости.

Как показывает опыт, во многих случаях гидравлические потери приблизительно пропорциональны квадрату скорости потока. Поэтому в гидравлике с давних времен принят следующий общий способ выражения гидравлических потерь полного напора в линейных единицах:

(6)

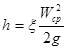
Такое выражение удобно тем, или в единицах давления

.

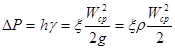
Такое выражение удобно тем, что включает в себя безразмерный коэффициент пропорциональности ξ, называемый коэффициентом сопротивления,и скоростной напор, входящий в уравнение Бернулли.

Гидравлические потери обычно подразделяют на два вида: местные потери и потери на трение.

Местные потери обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров канала (трубы), вызывающими деформацию потока. При этом происходят изменения скорости потока, возникают вихреобразования. Примерами местных сопротивлений могут служить устройства типа задержек потока, сопел, диафрагм, отверстий (шайб), поворотов, вентилей, кранов, другой стендовой арматуры. Местные потери энергии (напора) определяются по формулам:

или (7)

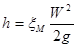
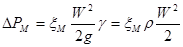
Последнее уравнение часто называют формулой Вейсбаха. В этих формулах W – средняя по сечению скорость в трубопроводе, в котором установлено местное сопротивление. Каждое местное сопротивление характеризуется своим значением коэффициента сопротивления ξ_М, которое во многих случаях приближенно можно считать постоянным для данного вида местного сопротивления.

Потери на трение, или потери по длине, — это потери энергии, которые в чистом виде возникают в прямых трубах постоянного сечения, т.е. при установившемся течении, и возрастают пропорционально длине трубы. Этот вид потерь обусловлен трением о поверхность и внутренним трением в жидкости, а поэтому они (потери) имеют место в трубах со сколь угодно малой шероховатостью стенок.

Потерю давления на трение можно выразить по общей формуле для гидравлических потерь, т.е. 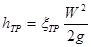, однако более удобнее будет коэффициент ξ_ТР связать с относительной длиной трубы ℓ/d соотношением ξ_ТР = λℓ/d.

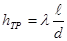
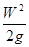
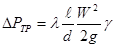
Тогда (8)

(9)

Формулу (9) обычно называют формулой Дарси. Безразмерный коэффициент λ называется коэффициентом потерь на трение или коэффициентом сопротивления трения.

Гидравлические потери в напорных потоках происходят за счет уменьшения вдоль потока удельной потенциальной энергии жидкости (Z + Р/γ). Удельная кинетическая энергия жидкости в этом случае если и меняется вдоль потока при заданном расходе, то не за счет потерь энергии, а вследствие изменения поперечного сечения канала, так как она зависит только от скорости, а скорость определяется объемным расходом Q и площадью сечения S: W = Q/S. Следовательно, в трубе постоянного сечения средняя скорость и удельная кинетическая энергия остаются строго постоянными, несмотря на наличие гидравлических потерь напора.

Расчет гидравлических потерь для разных конкретных случаев представляет собой один из основных вопросов гидравлики.

2. РЕЖИМЫ ТЕЧЕНИЯ ЖИДКОСТЕЙ В ТРУБАХ

Возможны два режима или два вида течения жидкостей в трубах: ламинарное, т.е. слоистое, течение и турбулентное, т.е. бурное, возмущенное.

Ламинарное течение – это течение без перемешивания слоев и частиц (макрочастиц) жидкости, без пульсаций скорости. Это течение является вполне упорядоченным и при постоянном напоре строго установившимся. Однако ламинарнре течение нельзя считать безвихревым. Хотя в нем нет ярко выраженных вихрей, но одновременно с поступательным движением жидкости имеет место упорядоченное вращательное движение отдельных частиц жидкости вокруг своих мгновенных центров вращения.

Турбулентное течение – это течение, сопровождающееся интенсивным перемешиванием жидкости и пульсациями скоростей и давлений. Движение отдельных частиц оказывается неупорядоченным, траектории фрагментов жидкости имеют подчас вид замысловатых кривых. Это объясняется тем, что при турбулентном течении наряду с продольным перемещением массы жидкости имеют место поперечное и вращательное движения отдельных , как бы автономных, объемов жидкости.

Смена режима течения данной жидкости в трубе происходит при определенной скорости течения, которую называют критической (W_кр). Как показывают эксперименты, значение этой скорости прямо пропорционально кинематическому коэффициенту вязкости (ν) и обратно пропорционально диаметру трубы (d), т.е. W_кр = kν/d. Оказывается, что входящий в предыдущее соотношение безразмерный коэффициет k имеет универсальное значение, т.е. он одинаков для всех жидкостей и труб любых диаметров. Это означает, что смена режимов течения происходит при вполне определенном соотношении, которое можно выразить числом, между скоростью, диаметром трубы и вязкостью жидкости. Это безразмерное число называется критическим числом Рейнольдса по имени английского ученого, который экспериментально установил этот критерий:

(10)

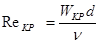
Как показывает опыт, критическое число Рейнольдса приблизительно равно 2300. Однако можно говорить не только о критическом числе Рейнольдса, определяющим смену режима течения, но и о числе Рейнольдса, характеным для того или иного потока, и выражать его через фактическую скорость потока, т.е.

(11)

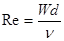
Таким образом, мы получили критерий, позволяющий судить о режиме течения жидкости в трубе. При значениях числа Rе Rе_КР течение обычно турбулентное.

Смена режимов течения при достижении числа Rе_КР объясняется тем, что один режим течения теряет устойчивость, а другой ее приобретает. При Rе Rе_КР, наоборот, турбулентный поток устойчив, а ламинарный – неустойчив. В связи с этим критическое число Рейнольдса, соответствующее переходу от ламинарного режима к турбулентному, может получиться несколько больше, чем для обратного перехода.

Гидродинамическое подобие. Гидродинамическое подобие – это подобие потоков несжимаемой жидкости, включающее в себя подобие геометрическое, кинематическое и динамическое.

Геометрическое подобие, как известно из геометрии, означает пропорциональность сходственных размеров и равенство соответствующих углов. В гидравлике под геометрическим подобием понимается подобие поверхностей, которые ограничивают потоки жидкостей, т.е. подобие трубных каналов.

Кинематическое подобие – это геометрическое подобие канала и пропорциональность скоростей в сходственных сечениях.

Динамическое подобие означает пропорциональность сил, действующих на сходственные элементы кинематически подобных потоков

Осуществление на практике полного гидродинамического подобия оказывается весьма затруднительным, поэтому имеют, обычно, дело с частичным (неполным) подобием, при котором наблюдается пропорциональность лишь главных, основных для процесса, сил.

Физический смысл числа Рейнольдса заключается в том , что это – величина, пропорциональная отношению динамического давления к напряжению трения или, что то же самое, отношение сил инерции к силам вязкости. Поэтому закон гидродинамического подобия формулируется следующим образом: для гидродинамического подобия геометрически подобных потоков с учетом сил вязкости требуется равенство чисел Рейнольдса, подсчитанных для любой пары сходственных сечений этих потоков.

МЕСТНЫЕ ГИДРАВЛИЧЕСКИЕ СОПРОТИВЛЕНИЯ

Мы уже говорили, что гидравлические потери энергии делятся на две категории: местные потери и потери на трение. Рассмотрим более подробно потери, обусловленные местными гидравлическими сопротивлениями, т.е. такими элементами трубопровода, в которых вследствие изменения размеров или конфигурации канала происходит изменение скорости потока и возникают вихреобразования. Общий способ их выражения основан на экспериментальных данных и имеет следующий вид:

, (12)

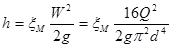
где Q – объемный расход, м 3 /с.

Задача теперь заключается в том, чтобы научиться определять коэффициенты сопротивления для различных трубных элементов, т.е. местных сопротивлений.

Простейшие местные гидравлические сопротивления можно разбить на следующие группы и подгруппы:

1. Расширение трубопровода (канала) – внезапное, плавное.

2. Сужение трубопровода (канала) – внезапное, плавное.

3. Поворот трубопровода (канала) – внезапный, плавный.

Более сложные случаи местных сопротивлений представляют собой комбинации перечисленных простейших сопротивлений. Рассмотрим некоторые местные сопротивления при турбулентном режиме течения. Следует отметить, что коэффициенты сопротивления ξ_М при турбулентном течении определяются почти исключительно формой гидравлического элемента и очень мало меняются с изменением размеров канала, скорости потока и вязкости жидкости. Поэтому их считают независящими от числа Рейнольдса, что означает автомодельность по числу Rе.

Значения коэффициентов местных сопротивлений в большинстве случаев получают экспериментальным путем, а затем пользуются обобщенными формулами или графиками. Однако для некоторых типов местных сопротивлений, а именно для внезапного расширения или для течения в диффузоре расчетные значения коэффициентов сопротивления имеют удовлетворительную точность. ДАЛЕЕ СЛЕДУЕТ ДЕМОНСТРАЦИЯ РИСУНКОВ МЕСТНЫХ ГИДРАВЛИЧЕСКИХ СОПРОТИВЛЕНИЙ, ВКЛЮЧАЯ СХЕМУ ВЕНТИЛЯ(рис.2)

Местные гидравлические сопротивления при ламинарном режиме.

Расчет потери напора на местных сопротивлениях при ламинарном режиме имеет особенности. Во — первых, местные сопротивления ври этом режиме играют меньшую роль по сравнению с потерями трения. Во – вторых, закон сопротивления в этом случае является более сложным и исследован в меньшей степени, чем при турбулентном режиме.

Если при турбулентном режиме потери напора на мастном сопротивлении не зависят от числа Рейнольдса, то при ламинарном режиме потерю напора h_м следует рассматривать как сумму:

где h_тр – потеря напора, обусловленная непосредственным действием сил трения (вязкости) в данном местном сопротивлении, пропорциональная вязкости жидкости и скорости в первой степени;

h_вихр – потеря, связанная с отрывом потока и вихреобразованиями, возникающими в самом местном сопротивлении или за ним, и пропорциональная квадрату скорости. Так, например, при течении через жиклер (рис. 3) слева от сечения 1. – 1 возникает потеря напора на трение, а справа – на вихреобразования. Формулу (12) можно представить в следующем виде:

, (14)

где А и В – безразмерные константы, зависящие от формы местного сопротивления. Разделив, согласно общему принципу определения коэффициента сопротивления, h_м на скоростной напор, получим общее выражение для коэффициента местного сопротивления при ламинарном режиме

(15)

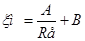
Соотношение между первым и вторым членами в формулах (14 и 15) зависит от формы местного сопротивления и числа Rе.

При широком диапазоне изменения числа Рейнольдса в одном и том же местном сопротивлении возможны как линейный (при малых числах Rе) так и квадратичный (при больших числах Rе) законы сопротивления, а также переходная между ними область сопротивления при средних числах Rе. Типичный график, иллюстрирующий сказанное, приведен на рис. . Такого рода графики для конкретных сопротивлений обычно строят на основе экспериментальных данных.

Иногда вместо двухчленной формулы выражения местных гидравлических потерь применяют степенной одночлен вида

h_м = kQ m , (16)

где k – размерная величина; m – показатель степени, зависящий от формы местного сопротивления и числа Рейнольдса и изменяющийся в пределах от 1 до 2.

ТЕЧЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ

Ламинарное течение жидкости в круглой трубе.Как уже говорилось,ламинарное течение является строго упорядоченным слоистым течением без перемешивания жидкости; оно подчиняется закону трения Ньютона, суть которого в следующем: касательное напряжение в жидкости зависит от рода жидкости и характера течения и при слоистом течении изменяется прямо пропорционально поперечному градиенту скорости, т.е.

,

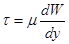
где μ – динамический коэффициент вязкости; наряду с динамическим коэффициентом вязкости μ применяется в гидравлике кинематический коэффициент вязкости ν, равный ν = μ/ρ, где ρ – плотность жидкости. (Размерность μ, н·сек / м 2 ; размерность ν, м 2 /сек).

Используя этот закон, находится распределение скоростей по сечению круглой трубы в ламинарном режиме течения жидкости и формула для определения расхода:

, (17)

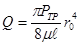
где Р_тр – перепад давления на участке трубы длиной ℓ, т.е. это потери от трения (потери трения).

Зная, что потери напора за счет трения определяются как h_тр = Р_тр/γ, находим

(18)

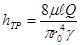
Заменяя μ через νρ и γ через ρg , а также переходя от r₀ к d = 2r₀, окончательно находится выражение

(19)

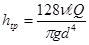
Полученный закон сопротивления показывает, что при ламинарном течении жидкости в круглой трубе потеря напора на трение пропорциональна расходу (скорости) и вязкости в первой степени и обратно пропорциональна диаметру в четвертой степени. Этот закон, часто называемый законом Пуазейля – Хагена, используется для расчета трубопроводов с ламинарным режимом течения.

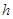
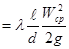
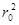
Так как по общему принципу (закон Дарси) _{тр ,} тогда, заменяя Q = W_ср π , окончательно получим . (20)

Связь средней скорости с потерей напора

Сопоставляя полученное выражение с формулой Дарси, видим,

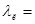
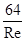
что (21)

Эту зависимость называют законом Пуазейля.

Зная закон распределения скоростей по сечению трубы и связь средней скорости с потерей напора, возможно определить значение коэффициента α, учитывающего неравномерность распределения скоростей в уравнении Бернулли (5).

Для ламинарного течения α₁ = α₂ =2

Теория ламинарного течения жидкости в круглой трубе, элементы которой были изложены в данном курсе, в общем хорошо подтверждается опытом. Полученные законы сопротивления и распределения скоростей не нуждаются в каких-либо поправках, за исключением следующих случаев.

1. При течении в начальном участке трубы, где происходит постепенное установление параболического профиля скоростей. Сопротивление на этом участке получается больше, чем на последующих участках трубы. Но это обстоятельство учитывается только при расчете очень коротких труб.

2. При течении со значительным теплообменом.

3. При очень высоких перепадах давления.

Потеря напора на участке трубы, длина которого ℓ меньше длины начального участка ℓ_нач, определяется по формулам (20 и 21), но с поправочным коэффициентом К, большим единицы. Так при ℓ = ℓ_нач К = 1,09. Для коротких труб значение поправочного коэффициента К существенно отличается от единицы. Определить длину начального участка можно по приближенной формуле Шиллера:

В литературных источниках встречаются и другие оценочные зависимости для определения длины начального участка

В том случае, когда длина трубы ℓ больше длины начального участка ℓ_нач, потеря напора будет складываться из потери на начальном участке и потери на участке стабилизированного течения:

или с учетом (21) и (22)

Если относительная длина трубопровода ℓ/d достаточно велика, то дополнительный член в скобках, равный 0,165 можно не учитывать.

Течение с теплообменом.При течении жидкости, которое сопровождается ее охлаждением, слои жидкости, непосредственно прилегающие к стенке, имеют температуру более низкую, а вязкость более высокую, чем в основном ядре потока. Это ведет к более сильному торможению пристенных слоев жидкости и уменьшению градиента скорости у стенки.

При течении, сопровождающемся нагреванием жидкости через стенку, ситуация меняется наоборот: вязкость пристенных слоев уменьшается, пристенный градиент скорости возрастает.

Таким образом, в результате теплообмена через стенку трубы происходит нарушение обычного параболического закона распределения скоростей. Это показано на рис. . Здесь 1 – распределение скоростей при изотермическом течении, 2 – при течении с охлаждением, 3 – при течении с нагреванием. Это вызывает изменение коэффициента α в уравнении Бернулли: охлаждение ведет к усилению неравномерности распределения скоростей (α > 2), нагревание ослабляет эту неравномерность (α 6 , α = 1,025,т.е. α асимптотически приближается к единице.

В большинстве случаев для практических расчетов, связанных с турбулентным течением жидкостей в трубах, пользуются экспериментальными данными, систематизированными на основе гидродинамической теории подобия. Основной расчетной формулой для турбулентного течения в круглых трубах является уже рассмотренная нами универсальная формула:

,здесь λ ≡ λ_Т – коэффициент потерь на трение при турбулентном режиме

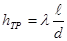
или ,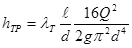

если скорость потока выразить через расход.

Видим, что при турбулентном течении потеря напора на трение пропорциональна квадрату скорости потока (и квадрату расхода). Но из закона гидродинамического подобия следует, что коэффициент λ_Т как и коэффициент λ_Л должен являться функцией числа Рейнольдса, содержащего скорость потока, вязкость жидкости и диаметр трубы

Существует ряд эмпирических и полуэмпирических формул, представляющих эту зависимость для турбулентного течения в гладких трубах. Одной из наиболее удобных и употребительных зависимостей является формула Конакова, которая имеет следующий вид:

(24)

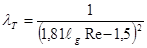
Эта формула применима от Rе = Rе_кр до Rе, равного нескольким миллионам. При числах Рейнольдса от 2300 до ≈ 10 5 можно пользоваться формулой Блазиуса

(25)

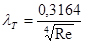
Из формул (24) и (25) видно, что коэффициент λ уменьшается с увеличением числа Рейнольдса, но это уменьшение гораздо менее значительно, чем при ламинарном режиме.

Приведенные формулы для определения коэффициента потерь на трение через число Rе справедливы для так называемых технически гладких (гидравлически гладких) труб, т.е. для таких, шероховатость которых столь мала, что практически не влияет на сопротивление. Именно такие трубы применяются в стендовой практике.

Экспериментально установлено, что при турбулентном режиме существуют три области, в которых коэффициент λ по-разному зависит от числа Rе:

1. Область гидравлически гладких труб.

2. Переходная область.

3. Область гидравлически шероховатых труб.

Физическая картина существования этих областей в одной и той же трубе объясняется следующим образом. У всякой трубы на стенке имеются выступы шероховатости. Их высота зависит от материала труб технологии их изготовления, времени эксплуатации и др. факторов. В турбулентном потоке скорости непосредственно у стенки равны нулю. Поэтому вблизи стенок образуется тонкий слой жидкости толщиной δ, где скорости столь малы, что в его пределах движение жидкости близко к ламинарному. Этот слой, толщина которого измеряется долями миллиметра, называется вязким (ламинарным) подслоем (рис. 4). Если через Δ обозначить среднюю высоту выступов шероховатости, то возможны следующие соотношения δ и Δ. При δ > Δ выступы шероховатости прикрыты вязким подслоем, турбулентная часть потока не касается выступов и скользит по ламинарному слою, как по гладкой трубе. В этом случае трубы рассматриваются как гидравлически гладкие и потери давление на трение не зависят от шероховатости трубы. Если δ

Кратко о гидродинамике: уравнения движения

Написав предыдущий пост, исторический и отчасти рекламный (хотя потенциальные абитуриенты такое вряд ли читают), можно перейти и к разговору «по существу». К сожалению, высокой степени популярности описания добиться вряд ли получится, но всё же постараюсь не устраивать курс сухих лекций. Хотя, от сухости избавиться не удалось, да и пост писался в результате ровно месяц.

В нынешней публикации описаны основные уравнения движения идеальной и вязкой жидкости. По возможности кратко рассмотрен их вывод и физический смысл, а также описаны несколько простейших примеров их точных решений. Увы, этими несколькими примерами доступные аналитически решения уравнений Навье-Стокса в значительной мере исчерпываются. Напомню, что Институт Клэя отнёс доказательство существования и гладкости решений к проблемам тысячелетия. Гении уровня Перельмана и выше — задача вас ждёт.

Понятие сплошной среды

В, если можно так выразиться, «традиционной» гидродинамике, сложившейся исторически, фундаментом является модель сплошной среды. Она отвлекается от молекулярной структуры вещества, и описывает среду несколькими непрерывными полевыми величинами: плотностью, скоростью (определяемой через суммарный импульс молекул в заданном элементе объёма) и давлением. Модель сплошной среды предполагает, что в любом бесконечно малом объёме содержится ещё достаточно много частиц (как принято говорить, термодинамически много — числа, близкие по порядку величины к числу Авогадро — 10 23 шт.). Таким образом, модель ограничена снизу дискретностью молекулярной структуры жидкости, что в задачах типичных пространственных масштабов совершенно несущественно.

Однако, такой подход позволяет описать не только воду в пробирке или водоёме, и оказывается куда более универсальным. Поскольку наша Вселенная на больших масштабах практически однородна, то, как ни странно, она начиная с некоторого масштаба превосходно описывается как сплошная среда, с учётом, конечно же, самогравитации.

Другими, более приземлёнными применениями сплошной среды являются описание свойств упругих тел, динамики плазмы, сыпучих тел. Также можно описывать топлу людей как сжимаемую жидкость.

Параллельно с приближением сплошной среды, в последние годы набирает обороты кинетическая модель, основанная на дискретизации среды на небольшие частицы, взаимодействующие между собой (в простейшем случае — как твердые шарики, отталкивающиеся при столкновении). Такой подход возник в первую очередь благодаря развитию вычислительной техники, однако существенно новых результатов в чистую гидродинамику не превнёс, хотя оказался крайне полезен для задач физики плазмы, которая на микроуровне не является однородной, а содержит электроны и положительно заряженные ионы. Ну и опять же для моделирования Вселенной.

Уравнение неразрывности. Закон сохранения массы

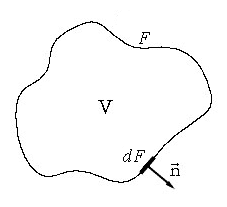
Самый элементарный закон. Пусть у нас есть какой-то совершенно произвольный, но макроскопический объём жидкости V, ограниченный поверхностью F (см. рис.). Масса жидкости внутри него определяется интегралом:

И пусть с жидкостью внутри него не происходит ничего, кроме движения. То есть, там нет химических реакций и фазовых переходов, нет трубок с насосами или чёрных дыр. Ну и всё происходит с маленькими скоростями и для малых масс вещества, потому никакой теории относительности, искривления пространства, самогравитации жидкости (она становится существенна на звёздных масштабах). И пусть сам объём и границы еего неподвижны. Тогда единственное, что может изменить массу жидкости в нашем объёме — это её перетекание через границу объёма (для определённости — пусть масса в объёме убывает):

где вектор j — поток вещества через границу. Точкой, напомним, обозначается скалярное произведение. Поскольку границы объёма, как было сказано, неподвижны, то производную по времени можно внести под интеграл. А правую часть можно преобразовать к такому же, как слева, интегралу по объёму по теореме Гаусса-Остроградского.

В итоге, в обеих частях равенства получается интеграл по одному и тому же совершенно произвольному объёму, что позволяет приравнять подинтегральные выражения и перейти к дифференциальной форме уравнения:

Здесь (и далее) использован векторный оператор Гамильтона. Образно говоря, это условный вектор, компоненты которого — операторы дифференцирования по соответствующим координатам. С его помощью можно очень кратко обозначать разного рода операции над скалярами, векторами, тензорами высших рангов и прочей математической нечистью, основные среди которых — градиент, дивергенция и ротор. Не буду останавливаться на них детально, поскольку это отвлекает от основной темы.

Наконец, поток вещества равен массе, переносимой через единичную площадку за единицу времени:

Окончательно, закон сохранения массы (называемый также уравнением неразрывности) для сплошной среды таков:

Это выражение наиболее общее, для среды, обладающей переменной плотностью. В реальности, эксперимент свидетельствует о крайне слабой сжимаемости жидкости и практически постоянном значении плотности, что с высокой точностью позволяет применять закон сохранения массы в виде условия несжимаемости:

которое с не менее хорошей точностью работает и для газов, пока скорость течения мала по сравнению со звуковой.

Уравнение Эйлера. Закон сохранения импульса

Весь относительно громоздкий процесс колдовства преобразования интегралов, использованный выше, даёт нам не только уравнение неразрывности. Точно такие же по сути преобразования позволяют выразить законы сохранения импульса и энергии, и получить в итоге уравнения для скорости жидкости и для переноса тепла в ней. Однако пока не будем сильно торопиться, и займёмся не просто сохранением импульса, а даже сохранением импульса в идеальной несжимаемой жидкости — т.е. рассмотрим модель с полным отсутствием вязкости.

Рассуждения практически те же самые, только теперь нас интересует не масса, а полный импульс жидкости в том же самом объёме V. Он равен:

При тех же самых условиях, что и выше, импульс в объёме может меняться за счёт:

• конвективного переноса — т.е. импульс «утекает» вместе со скоростью через границу
• давления окружающих элементов жидкости
• просто за счёт внешних сил, например — от силы тяжести.

Соответствующие интегралы (порядок отвечает списку) дают такое соотношение:

Начнём их преобразовывать. Правда, для этого нужно воспользоваться тензорным анализом и правилами работы с индексами. Конкретнее, к первому и второму интегралам применяется теорема Гаусса-Остроградского в обобщённой форме (она работает не только для векторных полей). И если перейти к дифференциальной форме уравнения, то получится следующее:

Крестик в кружочке обозначает тензорное произведение, в данном случае — векторов.

В принципе, это уже уравнение Эйлера, однако его можно чуток упростить — ведь закон сохранения массы никто не отменял. Раскрыв здесь скобки в дифференциальных операторах и приведя затем подобные слагаемые, мы увидим, что три слагаемых благополучно собираются в уравнение неразрывности, и потому дают в сумме ноль. Итоговое уравнение оказывается таким:

Если перейти в систему отсчёта, связанную с движущейся жидкостью (не будем заострять внимание на том, как это делается), мы увидим, что уравнение Эйлера выражает второй закон Ньютона для единицы объёма среды.

Учёт вязкости. Уравнение Навье-Стокса

Идеальная жидкость, это, конечно, хорошо (правда, всё равно точно не решается), но во многих случаях учёт вязкости необходим. Даже в той же конвекции, в течении жидкости по трубам. Без вязкости вода вытекала бы из наших кранов с космическими скоростями, а малейшая неоднородность температуры в воде приводила бы к её крайне быстрому и бурному перемешиванию. Потому давайте учтём сопротивление жидкости самой себе.

Дополнить уравнение Эйлера можно различными (но эквивалентными, конечно же) путями. Воспользуемся базовой техникой тензорного анализа — индексной формой записи уравнения. И пока также отбросим внешние силы, чтобы не путались под руками / под ногами / перед глазами (нужное подчеркнуть). При таком раскладе всё, кроме производной по времени, можно собрать в виде дивергенции одного такого тензора:

По смыслу, это плотность потока импульса в жидкости. К нему и нужно добавить вязкие силы в виде ещё одного тензорного слагаемого. Поскольку они явно приводят к потере энергии (и импульса), то они должны вычитаться:

Идя обратно в уравнение с таким тензором, мы получим обобщённое уравнение движения вязкой жидкости:

Оно допускает любой закон для вязкости.

Принято считать очевидным, что сопротивление зависит от скорости движения. Вязкость же, как перенос импульса между участками жидкости с различными скоростями, зависит от градиента скорости (но не от самой скорости — тому мешает принцип относительности). Если ограничиться разложением этой зависимости до линейных слагаемых, получится вот такой жутковатый объект:

в котором величина перед производной содержит 81 коэффициент. Однако, используя ряд совершенно разумных предположений об однородности и изотропности жидкости, от 81 коэффициента можно перейти всего к двум, и в общем случае для сжимаемой среды, тензор вязких напряжений равен:

где η (эта) — сдвиговая вязкость, а ζ (зета или дзета) — объёмная вязкость. Если же среда ещё и несжимаема, то достаточно одного коэффициента сдвиговой вязкости, т.к. второе слагаемое при этом уходит. Такой закон вязкости

носит название закона Навье, а полученное при его подстановке уравнение движения — это уравнение Навье-Стокса:

Точные решения

Главной проблемой гидродинамики является отсутствие точных решений её уравнений. Как бы с этим ни боролись, но получить действительно всеобщих результатов не удаётся до сих пор, и, напомню, вопрос существования и гладкости решений уравнений Навье-Стокса входит в список Проблем тысячелетия института Клэя.

Однако, несмотря на столь грустные факты, некоторые результаты есть. Здесь будут представлены далеко не все, а лишь самые простые случаи.

Потенциальные течения

Особый интерес представляют течения, в которых жидкость не завихряется. Для такой ситуации можно отказаться от рассмотрения векторного поля скорости, поскольку она выражается через градиент скалярной функции — потенциала. Потенциал же удовлетворяет хорошо изученному уравнению Лапласа, решение которого полностью определяется тем, что задано на границах рассматриваемой области:

Более того, при отсутствии вязкости из уравнения Эйлера можно однозначно выразить и давление, что вовсе замечательно и приводит нас к полному решению задачи. Ах, если бы так было всегда… то гидродинамики, наверное, уже бы и не было как современной и актуальной отрасли.

Дополнительно можно упростить задачу предположением, что течение жидкости двумерно — скажем, всё движется в плоскости (x,y), и ни одна частица не перемещается вдоль оси z. Можно показать, что в таком случае скорость может быть также заменена скалярной функцией (на этот раз — функцией тока):

которая при потенциальном течении удовлетворяет условиям Коши-Лагранжа из теории функций комплексной переменной и воспользоваться соответствующим математическим аппаратом. Полностью совпадающим с аппаратом электростатики. Теория потенциальных течений развита на высоком уровне, и в принципе хорошо описывает большой спектр задач.

Простые течения вязкой жидкости

Решения для вязкой жидкости чаще всего удаётся получить, когда из уравнения Навье-Стокса благодаря свойствам симметрии задачи выпадает нелинейное слагаемое.

Сдвиговое течение Куэтта

Самая элементарная задачка. Канал с неподвижной нижней и подвижной верхней стенкой, которая движется равномерно с некоторой скоростью. На границах жидкость прилипает к ним, так что скорость жидкости равна скорости границы. Этот результат является экспериментальным фактом, и как-то даже авторы первых экспериментов не упоминаются, просто — по совокупности экспериментов.

В такой ситуации от уравнения Навье-Стокса останется уравнение вида v» = 0, и потому профиль скорости в канале окажется линейным:

Данная задача является практически базовой для теории смазки, т.к. позволяет непосредственно определить силу, которую требуется приложить к верхней стенке для её движения с конкретной скоростью.

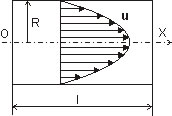
Течение Пуазейля

Вторая по элементарности — ламинарное течение в канале. Или в трубе. Результат оказывается один — профиль скорости является параболическим:

На основе решения Пуазейля можно определить расход жидкости через сечение канала, но, правда, только при ламинарном течении и гладких стенках. С другой стороны, для турбулентного потока и шероховатых стенок точных решений нет, а есть лишь приближённые эмпирические закономерности.

Стекание слоя жидкости по наклонной плоскости

Тут — почти как в задаче Пуазейля, только верхняя граница жидкости будет свободной. Если предположить, что по ней не бегут никакие волны, и вообще сверху нет трения, то профиль скорости будет практически нижней половинкой предыдущего рисунка. Правда, если из полученной зависимости вычислить скорость течения для средней равнинной речки, она составит около 10 км/с, и вода должна самопроизвольно отправляться в космос. Наблюдаемые в природе низкие скорости течения связаны с развитой завихренностью и турбулентностью потока, которые эффективно увеличивают вязкость воды примерно в 1 млн. раз.

В следующем посте планируется рассказать о законе сохранения энергии и соответствующих ему уравнениях переноса тепла при течении жидкости.